Cours - Réduction du volume de données

[Diapositives du cours]

Nous nous intéressons ici à la première approche de passage à l’échelle, qui consiste à réduire fortement le volume de calculs à réaliser. Une première méthode est la diminution forte du volume de données, en choisissant un échantillon de données et/ou un nombre réduit de variables. Les résultats obtenus ainsi sont en général des approximations des résultats qui seraient issus des données complètes. Une autre méthode, examinée dans la séance de cours suivante, consiste à travailler sur toutes les données (et toutes les variables) mais en exploitant leurs caractéristiques de similarité afin de diminuer l’ordre de complexité des calculs à réaliser. Des méthodes hybrides peuvent également être employées, comme la réduction de l’ordre de complexité après réduction de dimension (permettant de diminuer l’impact de la malédiction de la dimension, cf. cette partie d’une séance suivante). Nous verrons que chacune de ces approches peut présenter dans certains cas des inconvénients majeurs, la seule solution étant alors le recours au calcul parallèle.

Si la diminution du volume de données à traiter est assez forte, une architecture classique, centralisée, peut s’avérer suffisante. Si les données disponibles présentent une « faible densité en information » alors cette approche ne produira pas de bons résultats : avec un échantillon trop petit, les « régularités » recherchées par la méthode de fouille ne se manifesteront pas suffisamment pour être détectables ; avec trop peu de variables, les « régularités » trouvées seront très incomplètes ou les capacités prédictives insuffisantes.

Calculs sur un échantillon

Nous examinons d’abord brièvement l’échantillonnage, qui vise à inférer des propriétés concernant toute la « population » de \(N\) données à partir d’un sous-ensemble (échantillon) de seulement \(n \ll N\) données. Une présentation détaillée peut être trouvée par exemple dans [Til01].

Une question importante abordée par la théorie de l’échantillonnage est la construction des échantillons, basée sur des méthodes non aléatoires ou des méthodes aléatoires. Dans la première catégorie on peut trouver la construction d’un échantillon par choix d’expert (une bonne connaissance du problème est supposée permettre à un expert de désigner les données ou les observations à retenir dans l’échantillon), par le volontariat (les observations concernent des individus qui se portent volontaires), etc. Ces méthodes répondent souvent à des considérations pragmatiques mais il est difficile de qualifier la représentativité de l’échantillon, donc la qualité de l’inférence qui est réalisée.

Parmi les méthodes aléatoires de construction d’échantillon nous mentionnons ici l’échantillonnage simple, l’échantillonnage stratifié et l’échantillonage en grappes (voir par ex. [Til01] pour d’autres méthodes et des présentations plus détaillées).

L’échantillonnage simple consiste à faire des tirages indépendants, habituellement sans remise, chaque donnée (ou observation) ayant la même probabilité d’être sélectionnée, \(p_s = \frac{n}{N}\).

L’échantillonnage stratifié considère que l’ensemble de données est constitué de sous-ensembles (ou strates) qui présentent une certaine homogénéité interne par rapport à l’étude. Un échantillonnage simple est ensuite appliqué dans chaque strate. Par rapport à l’application directe d’un échantillonnage simple à l’ensemble de la population, l’application d’un échantillonnage stratifié augmente la précision pour une même valeur de \(n\) (ou conserve la précision avec \(n\) plus faible). Il est par ailleurs possible de moduler la représentation des différents strates dans l’échantillon en choisissant une valeur de \(p_s\) adéquate dans chaque strate.

Exemple :

Pour une étude des pratiques des clients du commerce en ligne, on considère qu’il y a une certaine homogénéité à l’intérieur de chaque tranche de revenus. Si un échantillonnage simple est appliqué directement sur la population entière, la proportion relative de chaque tranche de revenus n’est pas bien conservée dans l’échantillon ; plus la population d’une tranche de revenus est faible, plus son taux de présence dans l’échantillon s’éloignera en général de \(p_s\). On applique alors un échantillonnage stratifié : on partitionne la population en tranches de revenus (1 tranche = 1 strate) et on applique un échantillonnage simple en imposant un même taux de sélection dans chaque tranche.

L’échantillonnage en grappes vise en général à simplifier la réalisation de l’étude. On considère que l’ensemble de données est constitué de sous-ensembles (ou « grappes ») tels que les différences intra-grappe sont plus fortes que les différences inter-grappe. On sélectionne alors au hasard des « grappes » et on examine tous les individus de chaque grappe choisie. Par rapport à un échantillonnage simple appliqué à l’ensemble de la population, l’échantillonnage en grappes facilite la réalisation de l’étude s’il est plus simple d’obtenir les données par grappes, tout en conservant la précision (si les différences sont plus fortes à l’intérieur de chaque grappe qu’entre les grappes).

Exemple :

Pour une étude des pratiques sportives des élèves de troisième en zone urbaine, on considère qu’il y a autant de diversité à l’intérieur d’un même collège qu’entre collèges. Avec un échantillonnage simple il faudrait vraisemblablement interroger quelques élèves de chaque collège de chaque zone urbaine. Un échantillonnage en grappes, avec 1 grappe = 1 collège, nous amènerait plutôt à sélectionner quelques collèges et à interroger tous les élèves de troisième de ces collèges, solution bien plus facile à mettre en œuvre.

Quelle que soit la méthode de construction d’échantillon utilisée, il est important de garder à l’esprit que la taille de l’échantillon doit être suffisante pour que les régularités supposées (qui seront recherchées) y trouvent un support satisfaisant.

Échantillonnage dans Spark

Dans Spark on trouve l’échantillonnage simple et l’échantillonnage stratifié comme méthodes de base pour les structures de données de l’API actuelle (DataFrame, Dataset) ou précédente (RDD) :

Échantillonnage simple, peut s’appliquer à tout DataFrame (ou Dataset) et retourne un DataFrame (ou Dataset) de même type : méthode sample(withReplacement: Boolean, fraction: Double, seed: Long): Dataset[T] ; fraction indique la probabilité de choisir chaque donnée. La taille de l’échantillon \(n\) ne peut pas être contrôlée de façon précise, chaque donnée étant sélectionnée avec une probabilité \(p_s\) (plus \(N\) sera grand, plus \(n\) approchera en général \(p_s \cdot N\)).

Échantillonnage stratifié, peut s’appliquer à tout DataFrame et retourne un DataFrame de même type : méthode sampleBy[T](col: String, fractions: Map[T, Double], seed: Long): DataFrame (dans DataFrameStatFunctions) ; fractions indique, pour chaque clé \(k\), la probabilité \(f_k\) de choisir chaque donnée et \(N_k\) est le nombre de données de clé \(k\) dans le RDD initial ; col est le nom de la colonne contenant les clés qui identifient les strates ; respecte de façon approximative la taille d’échantillon visée (\(f_k \cdot N_k\)).

Réduction de dimension

Considérons \(N\) données (observations) définies dans \(\mathbb{R}^m\). Une réduction de dimension consiste à obtenir une représentation des \(N\) données dans \(\mathbb{R}^k\), avec \(k \ll m\). Cette diminution du nombre de variables décrivant les données peut avoir plusieurs objectifs :

1. Réduire le volume de données à traiter, tout en conservant au mieux « l’information utile ». Il est nécessaire de définir d’abord ce qu’est information utile.

2. Améliorer le rapport signal / bruit et supprimant des variables non pertinentes. Il est nécessaire de définir d’abord ce qu’est une variable non pertinente.

3. Améliorer la « lisibilité » des données en mettant en évidence des relations entre variables ou groupes de variables ou en facilitant la visualisation. Il est nécessaire de définir d’abord ce qu’il faut mettre en évidence.

4. Atténuer la « malédiction de la dimension » (curse of dimensionality, voir cette partie d’une séance suivante).

Vu la multiplicité des objectifs et des critères associés, de nombreuses méthodes de réduction de dimension ont été définies.

Approches de réduction de dimension

La construction de méthodes de réduction de dimension suit une des deux approches suivantes : la sélection de variables et la transformation de variables.

La sélection de variables (feature selection, voir par ex. la synthèse de [TAL14]) consiste à choisir un sous-ensemble de \(k\) variables parmi les \(m\) variables initiales. Les variables sélectionnées gardent ainsi leur signification initiale, ce qui contribue à la lisibilité des modèles construits ultérieurement. Cette approche est potentiellement sous-optimale par rapport à la seconde approche qui est la construction de nouvelles variables.

Chaque méthode de sélection de variables fait partie d’une des catégories suivantes :

1. Méthodes de filtrage : basées sur des critères (par ex. minimisation de la redondance entre variables, maximisation de l’information mutuelle avec la classe à prédire) qui ne tiennent pas compte des résultats du modèle décisionnel ultérieur.

2. Wrappers : basées sur des mesures des performances du modèle décisionnel qui emploie les variables sélectionnées.

3. Méthodes intégrées (embedded) : l’opération de sélection est indissociable de la méthode de modélisation décisionnelle.

La sélection de variables est confrontée à un problème de complexité algorithmiquepour choisir \(k\) variables parmi \(m\), l’espace de recherche contient \(C_m^k\) possibilités. Afin d’éviter une recherche exhaustive dans cet espace, des méthodes approximatives sont adoptées (la solution est en général sous-optimale par rapport à celle d’une recherche exhaustive). Nous pouvons mentionner les approches suivantes :

1. Tri des \(m\) variables initiales par rapport à un critère de « pertinence » exprimable par variable individuelle, indépendamment des autres, puis sélection des \(k\) premières (par ex., dans Spark, sélection sur la base du test du \(\chi^2\) avec ChiSqSelector).

2. Construction incrémentale de l’ensemble de \(k\) variables : à chaque itération on ajoute la variable qui forme le meilleur ensemble avec celles déjà sélectionnées lors des itérations précédentes.

La transformation de variables (feature extraction, expression qui peut avoir une signification plus large) consiste à construire de nouvelles variables à partir des variables initiales. Cette approche présente plus de flexibilité par rapport à la seule sélection de variables. En revanche, si les variables initiales ont une signification précise, les nouvelles variables sont rarement interprétables.

Les nouvelles variables sont obtenues par des méthodes qui peuvent être (voir les figures suivantes)

1. Linéaires : trouver un sous-espace linéaire de dimension \(k\) dans l’espace initial \(\mathbb{R}^m\).

2. Non linéaires : trouver un sous-espace non linéaire de dimension \(k\) dans l’espace initial.

Fig. 5 Sous-espace bidimensionnel linéaire dans l’espace tridimensionnel

Fig. 6 Sous-espace bidimensionnel non linéaire dans l’espace tridimensionnel

Nous rappellerons brièvement dans la suite trois méthodes factorielles linéaires :

1. L’analyse en composantes principales (ACP), méthode à caractère exploratoire, adaptée à des données décrites par des variables quantitatives.

2. L’analyse factorielle discriminante (AFD), méthode à caractère exploratoire et décisionnel, adaptée à des données décrites par des variables quantitatives et appartenant à plusieurs classes.

3. L’analyse des correspondances multiples (ACM), méthode à caractère exploratoire, adaptée à des données décrites par des variables nominales.

Pour plus de détails concernant ces méthodes classiques vous êtes invités à consulter des sources externes (par ex. [CABB04], [Sap11], voir aussi le support en ligne de l’UE RCP208).

Analyse en composantes principales

L’ACP est une méthode d’analyse exploratoire des données : à partir d’un ensemble de \(N\) observations caractérisées par \(m\) variables quantitatives initiales, on cherche à condenser la représentation des données en conservant au mieux leur organisation globale. Pour cela, on représente les données sur \(k\) nouvelles variables (les composantes principales, \(k < m\)) obtenues comme des combinaisons linéaires des variables initiales, en conservant le plus de variance possible.

Dans l’analyse de données massives, l’ACP est principalement utilisée pour :

1. Condenser les données en conservant au mieux leur organisation globale.

2. Visualiser en faible dimension l’organisation prépondérante des données.

3. Interpréter les corrélations ou anti-corrélations entre multiples variables.

4. Interpréter les projections des prototypes de classes d’observations par rapport aux variables.

5. Préparer des analyses ultérieures en éliminant les sous-espaces dans lesquels la variance des données est très faible (assimilés, parfois à tort, à des sous-espaces de bruit, sans information utile).

Dans la matrice \(\mathbf{R}\) des données brutes chaque ligne correspond à une observation et chaque colonne à une variable initiale. L’ACP connaît plusieurs variantes, selon le pré-traitement appliqué à la matrice \(\mathbf{R}\) :

1. ACP générale : appliquée directement sur \(\mathbf{X} = \mathbf{R}\). Interviennent dans l’analyse à la fois la position du nuage d’observations par rapport à l’origine et la forme du nuage. Cette variante est utilisée rarement, essentiellement pour tenir compte du zéro naturel de certaines variables.

2. ACP centrée : centrage préalable des variables. La matrice analysée, \(\mathbf{X}\), est obtenue en transformant \(\mathbf{R}\) pour que chaque variable (chaque colonne) soit de moyenne nulle. Cela revient à s’intéresser à la forme du nuage d’individus par rapport à son centre de gravité. Cette variante est utilisée lorsque les variables initiales sont directement comparables (de même nature, intervalles de variation comparables).

3. ACP normée : réduction préalable des variables. La matrice analysée, \(\mathbf{X}\), est obtenue en transformant \(\mathbf{R}\) pour que chaque variable (chaque colonne) soit de moyenne nulle et d’écart-type unitaire. On s’intéresse donc à la forme du nuage d’individus après centrage et réduction des variables. Cette variante (la plus fréquemment rencontrée) est employée lorsque les variables (toutes quantitatives) sont de nature différente ou présentent des intervalles de variation très différents.

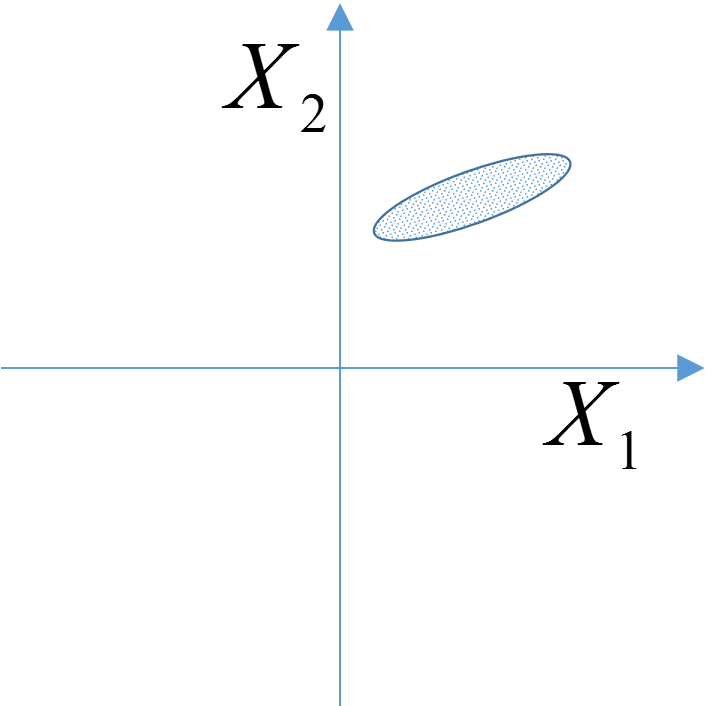
Fig. 7 ACP générale

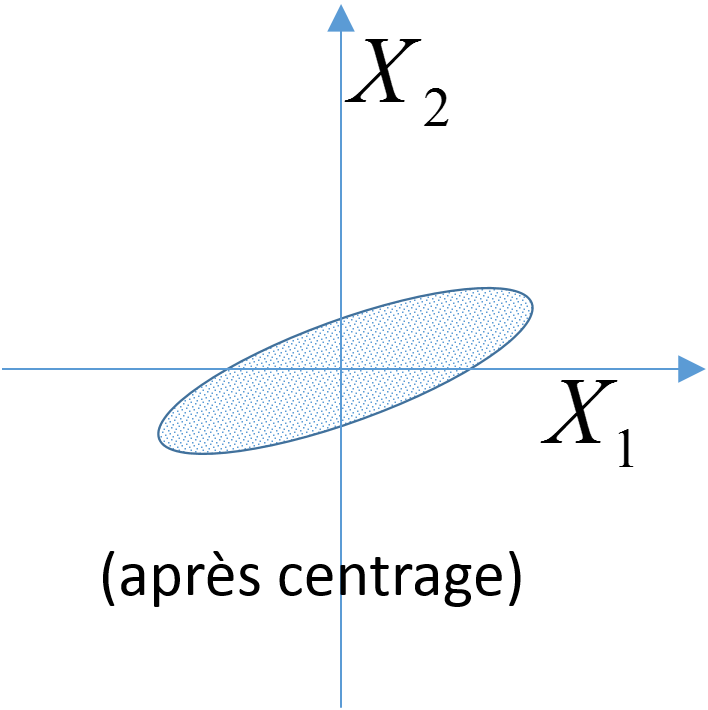
Fig. 8 ACP centrée

Fig. 9 ACP normée

Les lignes de la matrice analysée, \(\mathbf{X}\), décrivent les observations dans l’espace des variables initiales, alors que les colonnes de \(\mathbf{X}\) décrivent les variables dans l’espace des observations. Deux analyses sont donc possibles, l’analyse du nuage des observations et l’analyse du nuage des variables.

Dans l’analyse du nuage des observations nous cherchons \(k\) nouvelles variables obtenues comme des combinaisons linéaires des variables initiales (c’est à dire, un sous-espace linéaire de dimension \(k\) de l’espace initial) telles que la projection des observations sur ces variables conserve le plus de variance (ou « dispersion »).

Il est facile de montrer (voir par ex. [CABB04], [Sap11]) que le sous-espace de dimension \(k\) recherché est généré par les \(k\) vecteurs propres \(\mathbf{u}_{\alpha}\) associés aux \(k\) plus grandes valeurs propres \(\lambda_{\alpha}\) de la matrice \(\mathbf{X}^T \mathbf{X}\), satisfaisant donc l’équation \(\mathbf{X}^T \mathbf{X} \mathbf{u}_{\alpha} = \lambda_{\alpha} \mathbf{u}_{\alpha}\), \(\alpha \in \{1,\ldots,k\}\). Les vecteurs \(\mathbf{u}\) sont en général choisis de norme égale à 1. Rappelons ici que si \(\mathbf{u}_{\alpha}\) satisfait \(\mathbf{X}^T \mathbf{X} \mathbf{u}_{\alpha} = \lambda_{\alpha} \mathbf{u}_{\alpha}\) alors pour tout \(\beta \in \mathbb{R}\), \(\beta \mathbf{u}_{\alpha}\) satisfait la même relation.

Nous remarquerons que pour l’ACP centrée \(\mathbf{X}^T \mathbf{X}\) est la matrice des covariances empiriques alors que pour l’ACP normée \(\mathbf{X}^T \mathbf{X}\) est la matrice des corrélations empiriques.

La matrice \(\mathbf{X}^T \mathbf{X}\) est symétrique et (semi-)définie positive, donc toutes ses valeurs propres sont réelles, positives (certaines nulles si la matrice est semi-définie) et les vecteurs propres associés à des valeurs propres différentes sont orthogonaux.

La figure suivante montre un exemple d’analyse du nuage des observations. Les \(N = 5500\) données initiales de dimension \(m = 40\) sont projetées sur les deux premières composantes principales (\(k = 2\)) de l’analyse du nuage des observations. Les observations correspondent à des descripteurs visuels de pixels extraits d’images de textures [1]. En plus des 40 variables quantitatives initiales, chaque pixel est caractérisé par la classe de texture (11 classes au total) à laquelle il appartient, mais l’ACP ne tient pas compte de cette variable nominale. Cette classe a néanmoins été représentée par une couleur et une forme spécifique du point projection (11 classes au total) afin de nous permettre de voir dans quelle mesure les directions de variances maximales (les deux premiers axes principaux dans cette projection bidimensionnelle) permettent de séparer les classes.

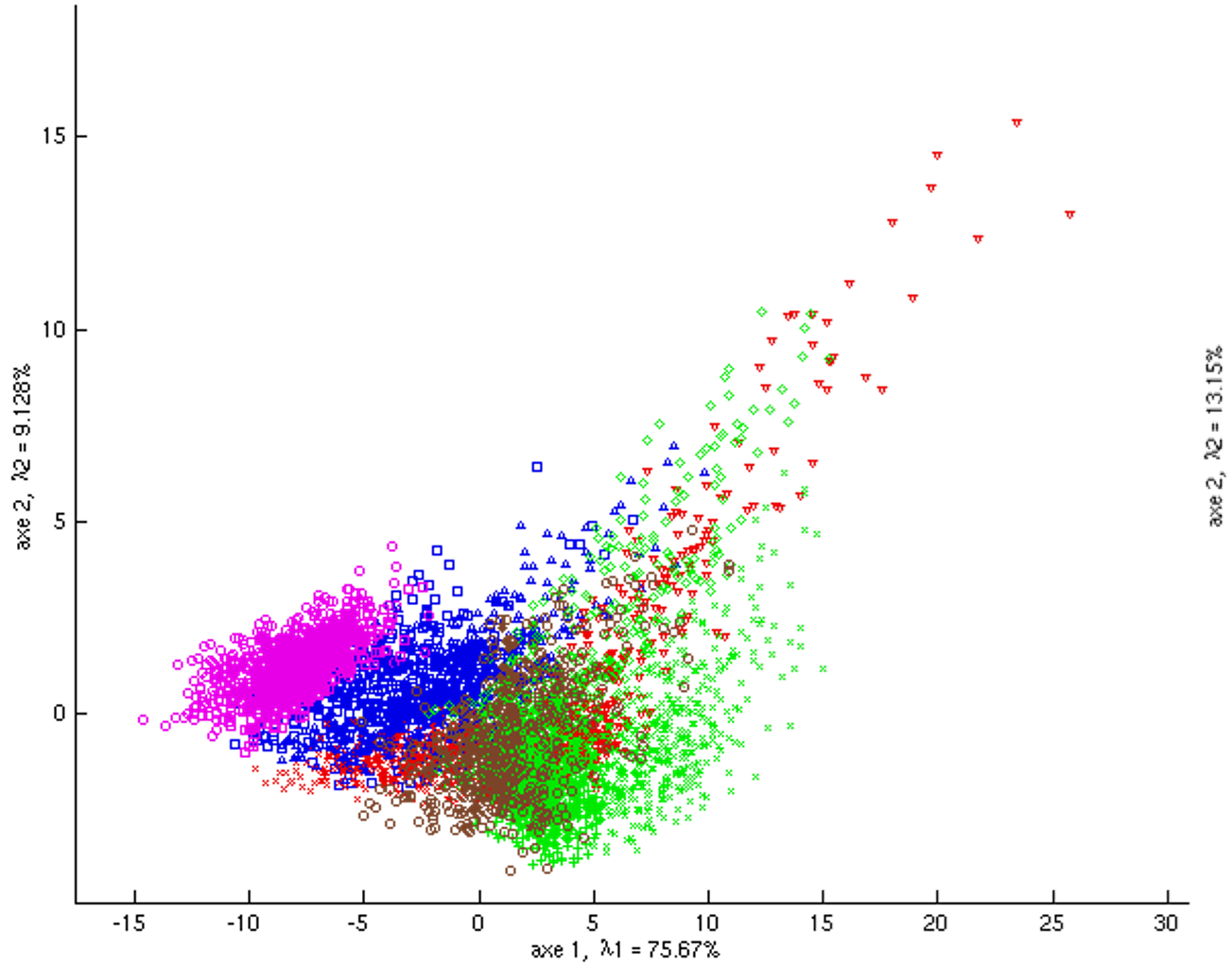
Fig. 10 Exemple 1 ACP : projection des observations sur le premier plan factoriel

L’analyse du nuage des variables se déroule de façon symétrique. La matrice à diagonaliser est dans ce cas \(\mathbf{X} \mathbf{X}^T\) et ses valeurs propres non nulles sont les mêmes que celles de \(\mathbf{X}^T \mathbf{X}\). Le lien entre les matrices analysées mène à des relations de transition entre les deux analyses (du nuage des observations et du nuage des variables) qui permettent d’obtenir les résultats de l’une directement à partir des résultats de l’autre (voir par ex. [CABB04], [Sap11]). Comme en général \(N \gg m\) (nombre d’observations \(\gg\) nombre de variables initiales), il est préférable de traiter la matrice \(\mathbf{X}^T \mathbf{X}\) de dimension \(m \times m\) plutôt que \(\mathbf{X} \mathbf{X}^T\) de dimension \(N \times N\).

La figure suivante montre un exemple d’analyse du nuage des variables pour un cas où les significations des variables initiales sont plus facile à appréhender [2] : poids du corps, poids du cerveau, durée de vie, durée de gestation, durée du sommeil avec rêves, sans rêves et totale, indice de prédation, indice d’exposition pendant le sommeil et indice de danger. Les 10 variables initiales sont projetées sur les deux premières composantes principales de l’analyse du nuage des variables. Chaque observation correspond à un représentant typique d’une espèce de mammifères ; il y a \(N = 62\) observations décrites par les \(m = 10\) variables initiales.

Le variables de départ étant de nature diverse (poids, durées, indices), l’ACP normée a été employée. Les variables initiales ont donc d’abord été centrées et réduites avant l’analyse (pour avoir une moyenne nulle et une variance égale à 1). Cela explique pourquoi chaque variable initiale est représentée par un vecteur de norme égale à 1, situé donc sur une hyper-sphère centrée dans l’origine. L’intersection de cette hyper-sphère avec le plan de projection illustré est donc un cercle et les vecteurs sont projetés à l’intérieur de ce cercle. Plus la projection d’une variable initiale est proche du cercle, plus cette variable est proche du plan de projection, donc bien représentée par ce plan.

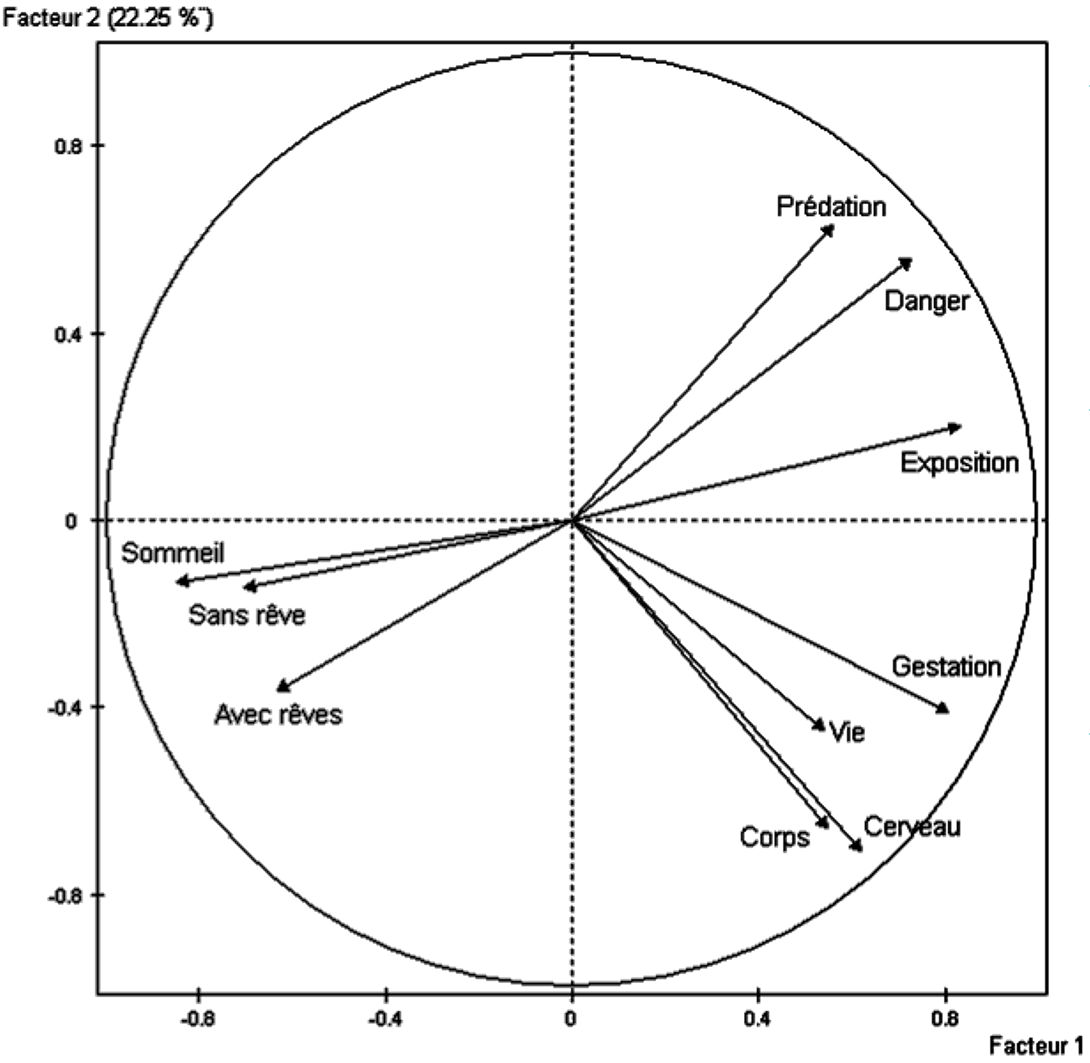
Fig. 11 Exemple 2 ACP : projection des variables sur le premier plan factoriel

Une visualisation simple permet d’identifier trois groupes de variables initiales (corrélation forte des variables à l’intérieur de chaque groupe) : le groupe « sommeil », le groupe « danger » et le groupe « corps, cerveau, vie, gestation » (CCVG). On observe une forte opposition entre le groupe « sommeil » et le groupe « danger » (anti-corrélation des variables entre ces deux groupes) et une opposition plus faible entre le groupe « sommeil » et le groupe CCVG.

Question : Si les projections de deux variables différentes (parmi les \(m > 2\) variables de départ) sur le plan des deux premiers axes factoriels sont confondues, nous pouvons conclure que

1. les deux variables sont identiques pour toutes les observations,

2. les deux variables ont les mêmes projections sur ces axes factoriels,

3. la corrélation entre les deux variables est égale à 1.

Le choix du nombre de composantes à retenir (valeur de \(k\)) dépend de l’objectif de l’analyse :

1. Analyse descriptive avec visualisation : déterminer à partir de quel ordre les différences entre les pourcentages d’inertie expliquée ne sont plus significatives. Un test statistique d’égalité entre valeurs propres successives peut être envisagé si la distribution des données est proche d’une distribution normale multidimensionnelle. Une méthode heuristique est souvent utilisée, voir la figure suivante : on construit le graphique des valeurs propres triées par ordre décroissant et on conserve les valeurs propres (et les composantes principales associées) qui précèdent le premier « coude ».

2. Réduction du volume de données : on impose la conservation d’une qualité d’approximation des données initiales, mesurée par le taux d’inertie expliquée (par ex. 85%). Le taux de réduction du volume interviendra, en général, dans ce choix.

3. Prétraitement avant application de méthodes décisionnelles : on utilise souvent un simple critère de bon conditionnement de la matrice des covariances empiriques (ou corrélations empiriques si analyse normée) ; attention, ce choix peut s’avérer nocif lorsque les directions qui présentent la plus faible variance sont des directions prédictives (par exemple, dans un problème de classement, des directions discriminantes ou qui aident à séparer les classes). Il est également possible de considérer le nombre d’axes comme un paramètre supplémentaire de la méthode décisionnelle et d’employer ensuite une technique de sélection de modèle décisionnel.

Fig. 12 Choix du nombre d’axes en ACP : lorsque les différences entre valeurs propres successives deviennent faibles, les axes principaux correspondants ne sont plus significatifs (deviennent très instables par rapport au choix de l’échantillon analysé)

Question : Considérons \(10^9\) observations décrites par \(m = 10\) variables quantitatives. Si ces observations sont issues d’une loi normale multidimensionnelle qui a la matrice identité d’ordre 10 comme matrice de variances-covariances, que pouvons-nous dire des valeurs propres ?

1. elles sont toutes identiques et égales à 1,

2. elles sont toutes de valeur proche de 1,

3. la plus grande est égale à 1, les autres sont égales à 0.

Les valeurs et vecteurs propres de \(\mathbf{M} = \mathbf{X}^T \mathbf{X}\) (en général \(N \gg m\), on s’intéresse donc à \(\mathbf{X}^T \mathbf{X}\) plutôt qu’à \(\mathbf{X} \mathbf{X}^T\)) peuvent être obtenus de différentes façons, selon qu’on souhaite déterminer toutes les valeurs propres de \(\mathbf{M}\) (de dimension \(m \times m\)) ou seulement les \(k\) plus grandes, avec les vecteurs propres unitaires associés.

Pour obtenir toutes les valeurs propres, l’algorithme est de complexité \(O(m^3)\) : on commence par calculer le déterminant de \((\mathbf{M} - \lambda \mathbf{I}_m)\) afin de trouver les valeurs propres, ensuite on résout pour chaque valeur propre un système linéaire de \(m\) équations avec \(m\) inconnues pour déterminer le vecteur propre associé. Si \(m\) est très élevé et on souhaite conserver \(k \ll m\) composantes, il est inutile de chercher à obtenir toutes les valeurs propres et on préfère la solution suivante.

Pour obtenir les \(k\) plus grandes valeurs propres, un algorithme itératif de complexité \(O(N m k)\) peut être employé. Les valeurs propres sont trouvées une par une (avec le vecteur propre associé), à partir de la plus grande. Pour cela, on itère \(\mathbf{x}_{i+1} = \frac{\mathbf{M} \cdot \mathbf{x}_i}{\left\|\mathbf{M} \cdot \mathbf{x}_i\right\|}\) à partir d’un vecteur \(\mathbf{x}_0\) quelconque non nul. A convergence, \(\lambda_1 = \mathbf{x}^T \cdot \mathbf{M} \cdot \mathbf{x}\) sera la plus grande valeur propre et le \(\mathbf{x}\) obtenu le vecteur propre associé. On calcule \(\mathbf{M}_2 = \mathbf{M} - \lambda_1 \mathbf{x} \cdot \mathbf{x}^T\) et on applique le même processus itératif sur \(\mathbf{M}_2\) pour obtenir \(\lambda_2\), etc. Cette solution est encore plus intéressante pour des variables initiales « creuses » : si chaque variable prend des valeurs non nulles pour au maximum \(p\) observations, avec \(p \ll N\), alors \(p\) remplace \(N\) dans la complexité qui devient donc \(O(p m k)\).

Question : Pour réduire le volume d’un ensemble de données nous souhaitons utiliser à la fois l’ACP et l’échantillonnage. Laquelle (lesquelles) des observations suivantes est (sont) juste(s) ?

1. appliquer l’ACP sur un petit échantillon permet de réduire significativement le coût de l’ACP

2. appliquer l’échantillonnage aux données projetées sur les premiers axes principaux permet de réduire significativement le coût de l’échantillonnage

3. les résultats de l’ACP sur un petit échantillon peuvent être éloignés des résultats sur les données complètes

4. la taille de l’échantillon n’a que très peu d’impact sur les résultats de l’ACP appliquée à l’échantillon

Analyse factorielle discriminante

L’AFD est une méthode d’analyse de données multidimensionnelles qui présente à la fois une composante descriptive et une composante décisionnelle. On considère \(N\) observations caractérisées par \(m\) variables quantitatives initiales (matrice de données \(\mathbf{X}\)) et une variable nominale de « classe » \(Y \in \{1,\ldots,q\}\). Lors de l’étape descriptive on cherche à identifier \(k\) « facteurs discriminants » (\(k < m\), \(k < q\) !) qui permettent de différencier au mieux les classes ; ces facteurs discriminants sont des combinaisons linéaires des variables initiales. Lors de l’étape décisionnelle on construit un modèle de discrimination (ou de classement) permettant de décider à quelle classe affecter une nouvelle observation à partir des valeurs prises par les variables quantitatives (donc implicitement par les facteurs discriminants).

Les principales utilisations de l’AFD sont :

1. Descriptive : condenser la représentation des données en conservant au mieux la séparation entre les classes.

2. Décisionnelle : classer de nouvelles observations à partir du sous-espace linéaire qui optimise la séparation.

Nous nous intéresserons ici exclusivement à la composante descriptive. Plus d’explications sur l’AFD (à la fois sur les aspects descriptifs et décisionnels) peuvent être trouvées par ex. dans [CABB04], [Sap11].

La figure suivante montre un exemple d’AFD. Les \(N = 5500\) données initiales de dimension \(m = 40\) issues de [1], avec \(q = 11\), sont projetées sur les deux premières composantes discriminantes (\(k = 2\)).

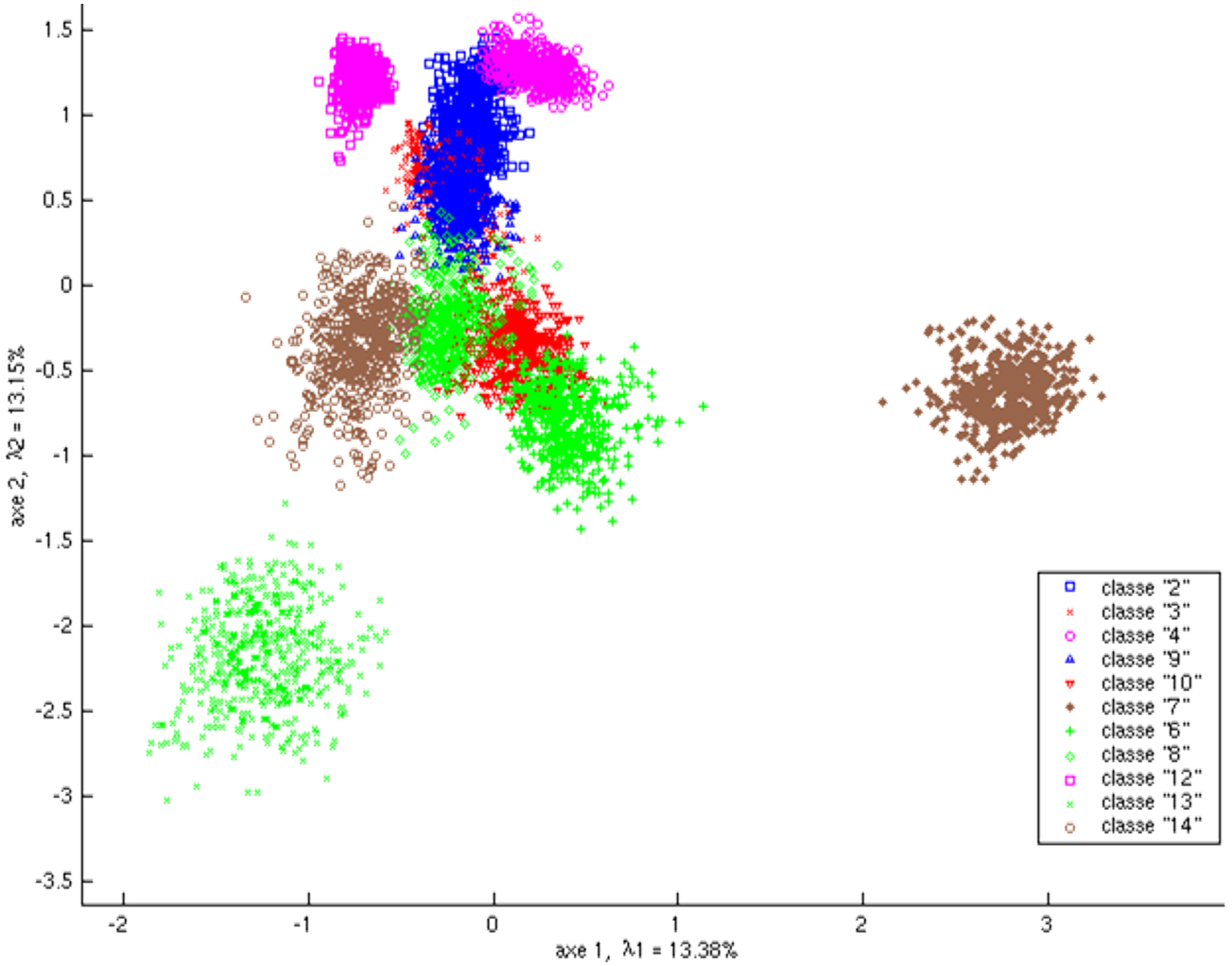
Fig. 13 Exemple 1 AFD : projection des observations sur le premier plan factoriel

En comparant le résultat avec la projection des mêmes données sur les deux premières composantes principales (voir plus haut) on constate que la séparation entre les classes est naturellement bien meilleure avec l’AFD. On voit aussi que cette séparation entre les 11 classes n’est pas parfaite sur le premier plan discriminant ; la séparation est en revanche presque parfaite dans l’espace tridimensionnel correspondant aux trois premières composantes discriminantes (non représenté ici).

La figure suivante illustre, pour un exemple simple (deux classes de forme allongée dans le plan), la différence entre l’ACP et l’AFD : l’ACP cherche le sous-espace (unidimensionnel ici) qui maximise la variance des projections alors que l’AFD cherche le sous-espace qui maximise la séparation entre les classes.

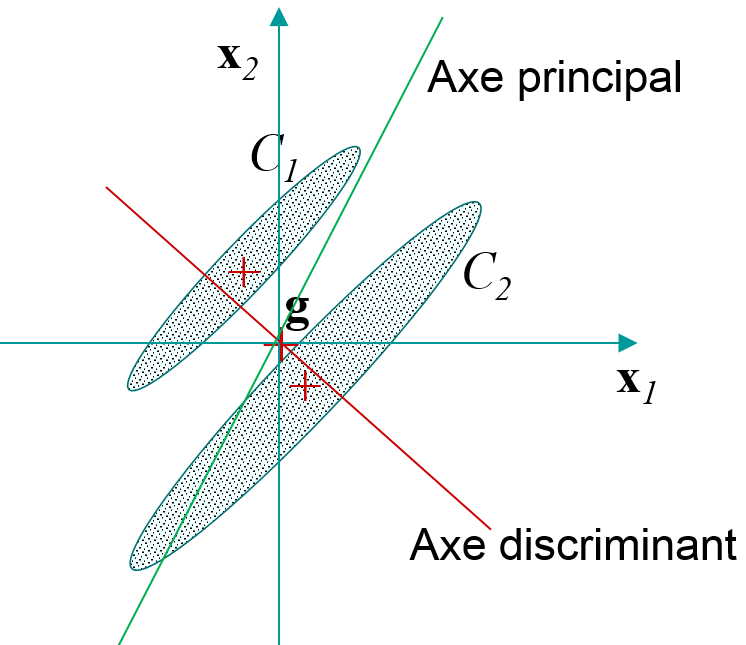
Fig. 14 AFD versus ACP

Pour comprendre de quelle façon l’AFD procède il est nécessaire de s’intéresser aux calculs des covariances entre les variables initiales, selon qu’on considère les données dans leur totalité ou séparées en classes :

1. Covariances inter-classes : calculées en considérant que les seules observations sont les centres de gravité des \(q\) classes \(\rightarrow\) matrice \(\mathbf{E}\).

2. Covariances intra-classes : calculées sur les observations de départ, en centrant chaque classe sur son centre de gravité \(\rightarrow\) matrice \(\mathbf{D}\).

3. Covariances totales : calculées sur les observations de départ \(\rightarrow\) matrice \(\mathbf{S}\).

Ces covariances sont liées par la relation de Huygens \(\mathbf{S} = \mathbf{E} + \mathbf{D}\).

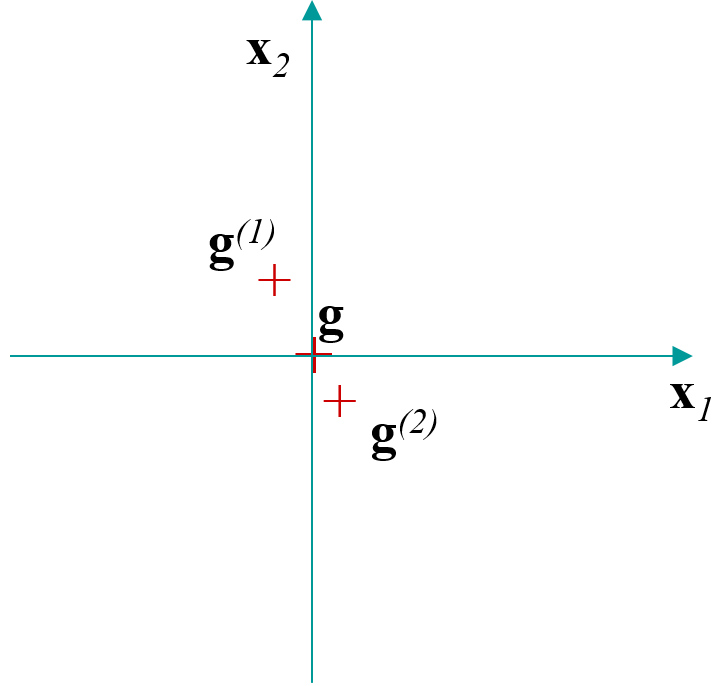
Fig. 15 Inter-classes

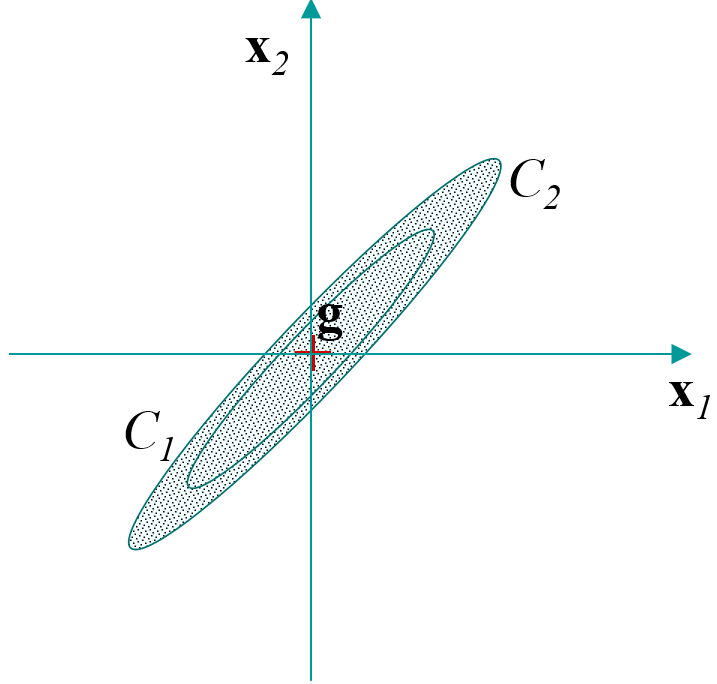
Fig. 16 Intra-classes

Fig. 17 Totale

Pour trouver le sous-espace de dimension \(k\) le plus discriminant on cherche à séparer au mieux les centres de gravité des classes, tout en tenant compte de la forme des classes. On peut montrer (voir par ex. [CABB04], [Sap11]) que le sous-espace recherché est généré par les \(k\) vecteurs propres \(\mathbf{u}_{\alpha}\) associés aux \(k\) plus grandes valeurs propres \(\lambda_{\alpha}\) de l’équation de valeurs et vecteurs propres généralisée \(\mathbf{E} \mathbf{u}_{\alpha} = \lambda_{\alpha} \mathbf{S} \mathbf{u}_{\alpha}\), \(\alpha \in \{1,\ldots,k\}\). Il est possible de résoudre plutôt \(\mathbf{E} \mathbf{u}_{\alpha} = \lambda_{\alpha} \mathbf{D} \mathbf{u}_{\alpha}\) si le rang de \(\mathbf{D}\) n’est pas inférieur à celui de \(\mathbf{S}\) (le rang de \(\mathbf{D}\) ne peut pas être supérieur à celui de \(\mathbf{S}\)). Aussi, si \(\mathbf{S}\) est inversible (et bien conditionnée) cela revient à résoudre \(\mathbf{S}^{-1} \mathbf{E} \mathbf{u}_{\alpha} = \lambda_{\alpha} \mathbf{u}_{\alpha}\).

Lorsque la matrice \(\mathbf{S}\) est singulière, une approche fréquente est de réduire la dimension avec une ACP, pour que dans l’espace réduit \(\mathbf{S}'\) soit de rang complet, ensuite résoudre \({\mathbf{S}'}^{-1} \mathbf{E}' \mathbf{u}_{\alpha} = \lambda_{\alpha} \mathbf{u}_{\alpha}\) dans cet espace réduit.

Remarque importante : si l’ACP est appliquée pour réduire la dimension au-delà de la nécessité de rendre \(\mathbf{S}'\) de rang complet (par exemple, pour rendre \(\mathbf{S}'\) bien conditionnée), il y a un risque non négligeable d’élimination de variables discriminantes ! Il faudrait préférer dans ce cas une approche de régularisation, par exemple remplacer \(\mathbf{S}\) par \(\mathbf{S} + r \mathbf{I}_m\) (où \(\mathbf{I}_m\) est la matrice identité d’ordre \(m\)). La constante de régularisation \(r > 0\) doit être assez grande pour que la matrice \(\mathbf{S} + r \mathbf{I}_m\) soit bien conditionnée (mais pas trop grande, pour éviter de dénaturer la solution).

Le choix du nombre de composantes discriminantes à retenir (valeur de \(k\)) peut être réalisé à l’aide de tests statistiques lorsqu’il est possible de considérer que les classes sont issues de lois normales multidimensionnelles :

1. Test de Rao : test d’égalité à 0 de la \(i\)-ème valeur propre.

2. Test du lambda de Wilks : test de l’apport des axes au-delà du \(i\)-ème.

3. Test incrémental : test de l’apport du \(i+1\)-ème axe.

Si l’AFD est employée comme un prétraitement avant application de méthodes décisionnelles, il est également possible de considérer le nombre d’axes (de facteurs discriminants) comme un paramètre supplémentaire de la méthode décisionnelle et de se servir ensuite d’une technique de sélection de modèle décisionnel pour choisir le nombre d’axes.

Il est important de noter que pour l’AFD (méthode linéaire) le nombre \(k\) de facteurs discriminants est \(k < q\), \(q\) étant le nombre de classes. En effet, avec \(q\) classes, le rang de \(\mathbf{E}\) ne peut être supérieur à \(q-1\) et donc l’équation \(\mathbf{E} \mathbf{u}_{\alpha} = \lambda_{\alpha} \mathbf{S} \mathbf{u}_{\alpha}\) ne peut avoir plus de \(q-1\) valeurs propres non nulles. Par exemple, pour un problème à 2 classes on ne peut trouver qu’un seul axe discriminant (\(k = 1\)).

Question : Est-ce utile ou potentiellement risqué de réduire la dimension par ACP avant d’appliquer l’AFD ? Pourquoi ? L’illustration qui suit cette question devrait vous aider à répondre. Plusieurs réponses peuvent être correctes.

1. utile pour obtenir une matrice \(\mathbf{S}\) bien conditionnée

2. utile pour réduire la complexité algorithmique de l’application de l’AFD

3. risqué car l’ACP mène à une réduction du nombre d’observations

4. risqué car perte potentielle d’information de discrimination

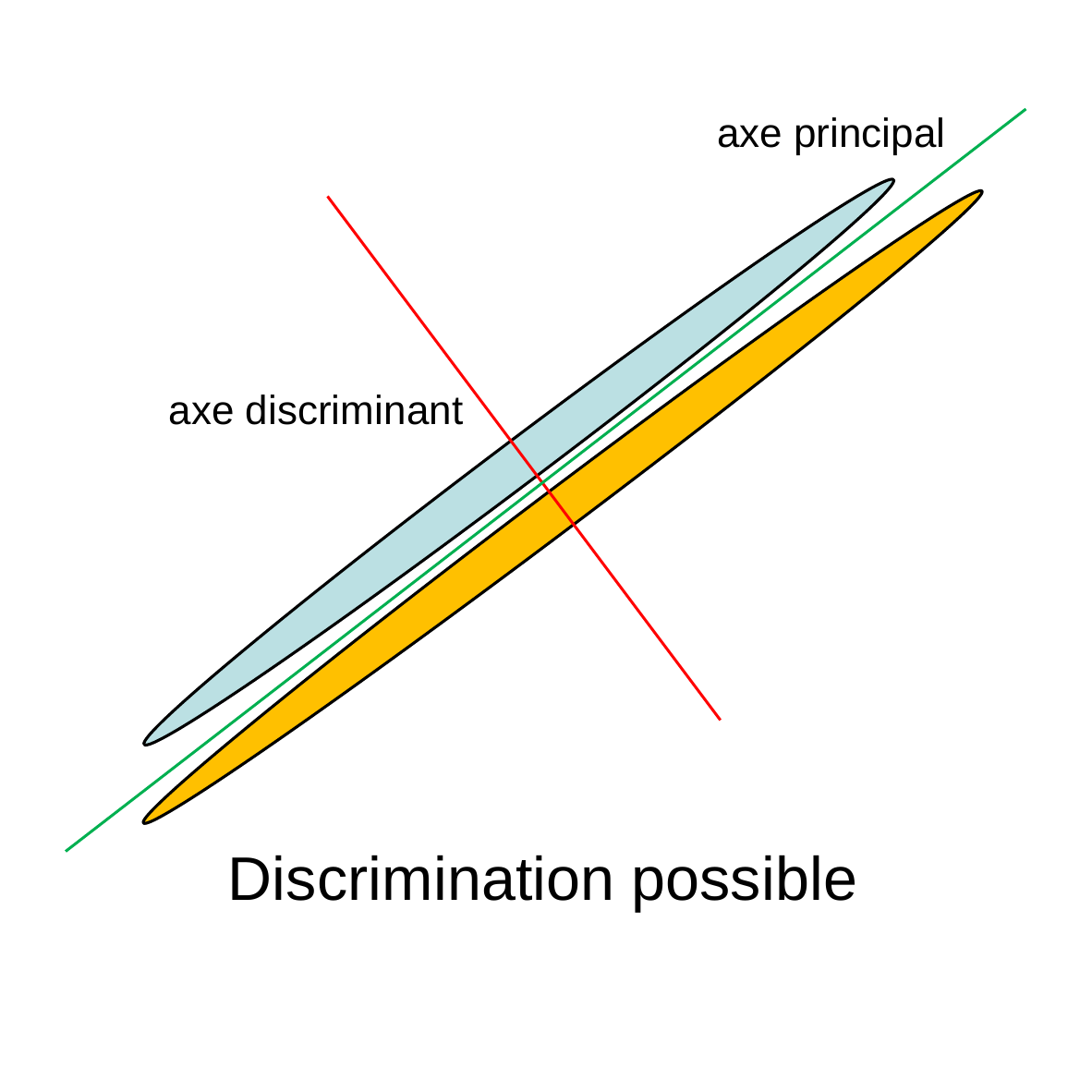
Fig. 18 Exemple simple AFD vs ACP. Chacune des deux ellipses regroupe les observations d’une des classes. La discrimination entre les deux classes est-elle encore possible si on projette d’abord les observations sur l’axe principal ?

Analyse factorielle des correspondances

L’analyse des correspondances est une méthode d’analyse exploratoire de données décrites par des variables nominales (à modalités). Nous examinerons brièvement ici l’analyse des correspondances multiples (ACM) qui considère \(N\) (ou \(n\)) observations caractérisées par \(q > 2\) variables nominales, représentées par un tableau disjonctif complet (TDC, voir la Fig. 19 ci-dessous) ; chaque observation possède exactement une modalité pour chaque variable.

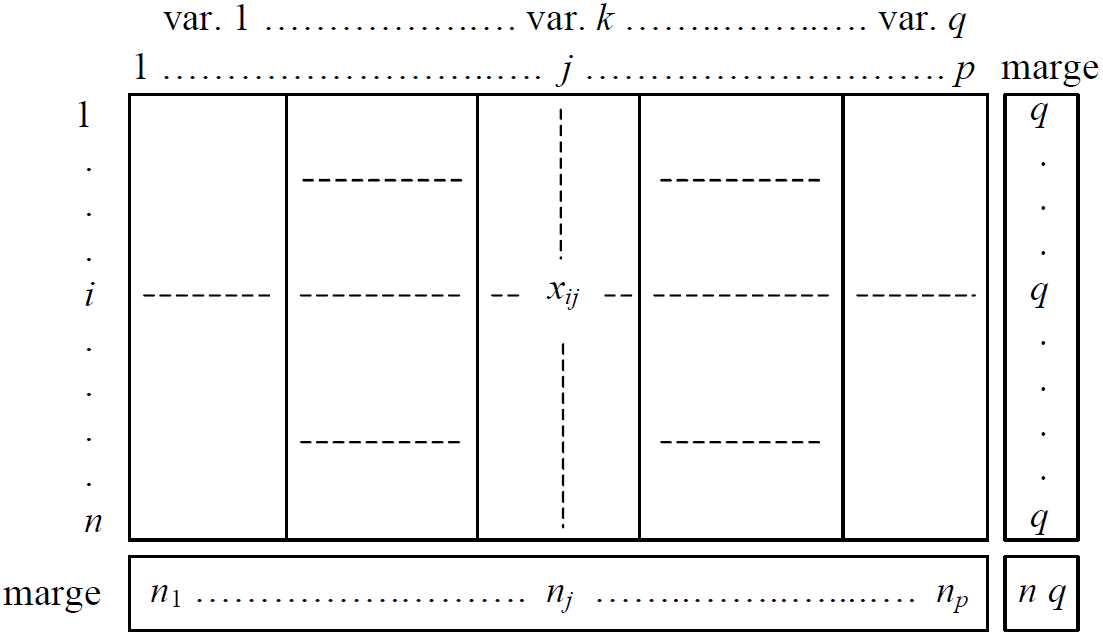
Fig. 19 Tableau disjonctif complet (TDC)

Il est également possible d’utiliser pour l’ACM un tableau de Burt qui est la concaténation des tables de contingences par paires de variables nominales. L’emploi du TDC permet d’analyser à la fois le nuage des observations et le nuage des modalités des variables, alors que le tableau de Burt permet d’étudier seulement le nuage des modalités (car les observations individuelles n’y sont pas décelables).

L’ACM cherche à mettre en évidence les relations dominantes entre des modalités des variables nominales initiales. Pour cela, \(k\) nouvelles variables quantitatives sont construites à partir des \(q\) variables nominales initiales, en conservant un maximum de variance.

L’ACM est utilisée traditionnellement dans le traitement d’enquêtes basées sur des questions fermées à choix multiples, afin de mettre en évidence des relations entre modalités ou éventuellement entre observations et modalités. Dans l’analyse de données massives, l’ACM peut servir à résumer un grand nombre (\(q\)) de variables qualitatives par un faible nombre (\(k \ll q\)) de variables quantitatives. Il est également possible d’inclure des variables quantitatives dans l’analyse, après leur transformation en variables nominales (voir plus loin).

Considérons un exemple issu de [CABB04] et basé sur des données de [3] pour clarifier la nature des résultats obtenus par ACM (sur des données en faible volume). L’enquête « Les étudiants et la ville » [3] dont sont issues les données inclut, entre autres, les questions suivantes :

1. Habitez-vous : seul(e), en colocation, en couple, avec les parents.

2. Quel type d’habitation occupez-vous : cité U, studio, appartement, chambre chez l’habitant, autre.

3. Si vous vivez en dehors du foyer familial, depuis combien de temps : moins d’1 an, de 1 à 3 ans, plus de 3 ans, non applicable (NA).

4. A quelle distance de l’université vivez-vous : moins d’1 km, de 1 à 5 km, plus de 5 km.

5. Quelle est la surface habitable de votre logement : moins de 10 \(m^2\), de 10 \(m^2\) à 20 \(m^2\), de 20 \(m^2\) à 30 \(m^2\), plus de 30 \(m^2\).

Nous pouvons observer que trois des cinq variables sont issues de variables quantitatives discrétisées avant la réalisation du sondage.

La figure suivante montre les résultats de l’analyse des modalités des variables nominales initiales à travers leurs projections sur les deux premiers facteurs :

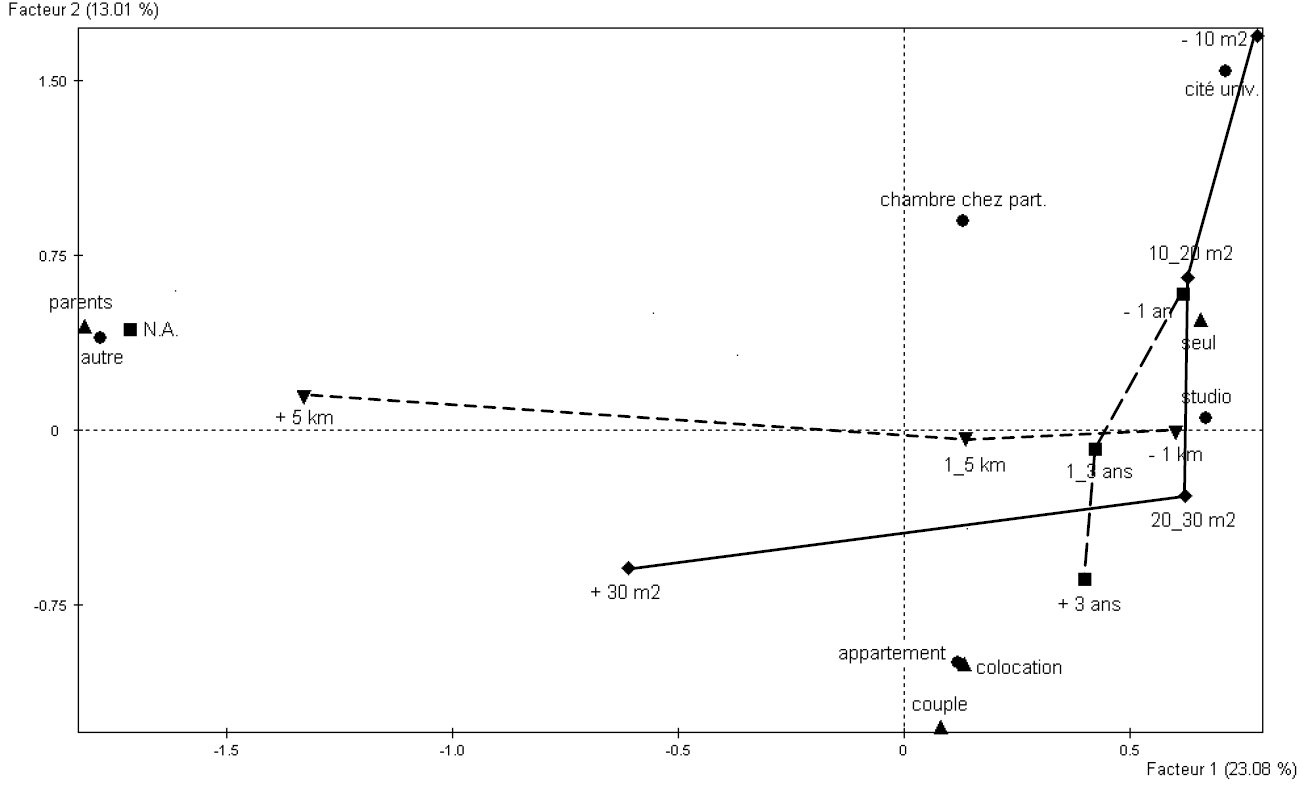
Fig. 20 ACM : résultats sur l’exemple « Les étudiants et la ville » [3]

Nous pouvons examiner des similarités et des oppositions entre projections de modalités de variables différentes (deux modalités sont similaires si elles concernent les mêmes populations d’observations) ou d’une même variable (et donc mutuellement exclusives ; deux telles modalités seront « similaires » si leurs populations sont similaires par rapport aux autres variables nominales). Sur cet exemple nous pouvons constater, par exemple, des similarités fortes entre les modalités « parents » (variable « Habitez-vous »), « NA » (variable « depuis combien de temps ») et « autre » (variable « type d’habitation »), ainsi que des oppositions fortes entre « seul » et « parents » (même variable « Habitez-vous »), ou entre « +5 km » et « -1 km » (variable « distance »). Pour améliorer la lisibilité, les modalités « successives » des variables ordinales (issues ici de la discrétisation préalable de variables quantitatives) ont été reliées entre elles par des traits.

Pour réaliser l’ACM on cherche, comme pour l’ACP, le sous-espace de dimension \(k\) qui résume le mieux la variance (on parle parfois de « dispersion ») du nuage analysé. En revanche, contrairement à l’ACP où les données (observations ou variables) sont en général non pondérées, pour l’ACM on pondère chaque modalité (représentée par une colonne du TDC) par sa fréquence relative. Aussi, pour l’ACM on emploie la distance du \(\chi^2\) qui permet de pondérer dans le calcul de distance l’influence de chaque composante par l’inverse de son poids. Des développements plus détaillés peuvent être trouvés par ex. dans [CABB04], [Sap11]. La distance du \(\chi^2\) présente une propriété intéressante d’équivalence distributionnelle : si deux colonnes (modalités) proportionnelles sont cumulées en une seule (fusion de deux modalités), les résultats de l’analyse ne changent pas.

Question : Comment interpréter la similarité entre les modalités « couple » et « colocation » de la variable « Habitez-vous » (voir la figure précédente) ?

1. les couples et les colocataires habitent en appartement,

2. les couples habitent en général en colocation,

3. les individus qui habitent en couple ou en colocation possèdent en général les mêmes modalités pour les autres variables.

Il est possible d’inclure des variables quantitatives dans l’ACM si les domaines de variation de ces variables sont découpés en intervalles et chaque intervalle est assimilé à une modalité de variable nominale. Cela permet de trouver des relations entre modalités de variables qualitatives et intervalles de valeurs prises par des variables quantitatives. Cela donne aussi la possibilité de mettre en évidence des relations non linéaires entre (intervalles de) valeurs prises par des variables quantitatives. Le découpage en intervalles du domaine de variation d’une variable quantitative peut être réalisé sur la base de connaissances a priori concernant les intervalles « pertinents » ou à partir de l’histogramme, comme dans la figure suivante (pour un découpage robuste, les frontières entre intervalles sont choisies dans les creux de l’histogramme) ; chaque intervalle sera une modalité de la nouvelle variable ordinale (les valeurs numériques sont ordonnées, les intervalles le seront donc aussi).

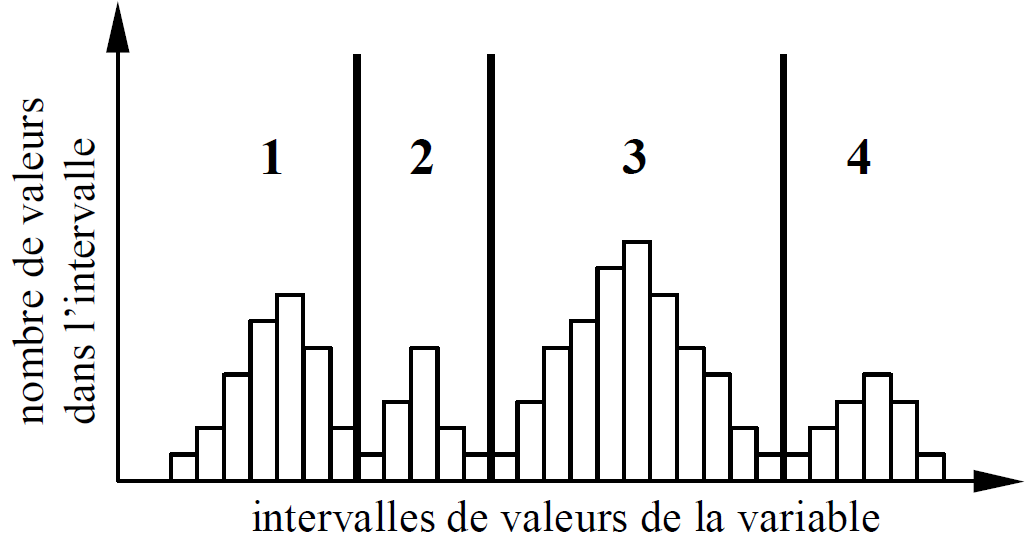
Fig. 21 Découpage en intervalles du domaine de variation d’une variable quantitative afin d’obtenir des modalités

Question : L’ACM permet de (plusieurs réponses peuvent être correctes)

1. déterminer les variables qui permettent de séparer les observations en classes,

2. trouver des corrélations linéaires entre variables,

3. représenter par quelques variables numériques des observations décrites au départ par des variables nominales,

4. mettre en évidence les relations dominantes entre modalités de variables nominales.

---

[CABB04] (1,2,3,4,5,6,7,8)

Crucianu, M., J.-P. Asselin de Beauville, et R. Boné. Méthodes d’analyse factorielle des données : méthodes linéaires et non linéaires. Hermès, Paris, 2004.

[Sap11] (1,2,3,4,5,6)

Saporta, G. Probabilités, Analyse des Données et Statistique. Technip, Paris, 2011.

[TAL14]

Tang, J., S. Alelyani, et H. Liu. Feature selection for classification: A review. Dans Data Classification: Algorithms and Applications, pages 37–64. 2014.

[Til01] (1,2)

Tillé, Y. Théorie des sondages. Dunod, Paris, 2001.

---

[1] (1,2)

Données mises à disposition par le Laboratoire de Traitement d’Image et de Reconnaissance de Formes (LTIRF) de l’Institut National Polytechnique de Grenoble (INPG) dans le cadre du projet ESPRIT III ELENA (No. 6891) et du groupe de travail ESPRIT ATHOS (No. 6620).

[2]

Données issues de Allison T., Cicchetti D., Sleep in mammals: ecological and constitutional correlates, Science, vol. 194, pp. 732-734.

[3] (1,2,3)

Données issues de l’enquête « Les étudiants et la ville » réalisée en 2001 sous la direction de S. Denèfle à l’Université de Tours, voir [CABB04].