Travaux pratiques - Introduction à GraphFrames : chemins et centralités¶
Références externes utiles :
Objectif du TP¶
Nous étudions ici une librairie pour Spark appelée GraphFrames, qui étend les fonctionnalités de Spark avec des algorithmes parallélisés pour traiter les problèmes de graphes.
Dans cette séance de travaux pratiques, nous utilisons un graphe de taille limitée, comprenant quelques villes des Pays-Bas et du Royaume Uni, et testons divers algorithmes de parcours du graphe. D’abord, autour de la notion de chemin, avec les plus courts chemins, tant en termes de nombre de nœuds visités, qu’en termes de distance parcourue entre les villes. Dans une seconde partie, nous étudions diverses centralités pour caractériser l’importance des nœuds dans le graphe.
Invocations initiales et chargement des données¶
import os,sys
os.environ['PYSPARK_PYTHON'] = sys.executable
os.environ['PYSPARK_DRIVER_PYTHON'] = sys.executable
os.environ['PYSPARK_SUBMIT_ARGS'] = '--packages graphframes:graphframes:0.8.1-spark3.0-s_2.12 pyspark-shell'
from graphframes import *
from pyspark.sql.types import *
import pyspark
from pyspark.context import SparkContext
from pyspark.sql.session import SparkSession
from pyspark.sql import SQLContext
from pyspark import SparkContext
sc = SparkContext()
sqlContext = SQLContext(sc)
spark = SparkSession(sc)
Créons un dossier pour nos données, puis téléchargeons-les :
# Crée un dossier data
dossier_tp = "data/"
archive_zip = "tp-chemins-centralites.zip"
fichier_csv = dossier_tp + "transport-nodes.csv"
if not os.path.exists(dossier_tp + archive_zip):
os.system("mkdir -p "+dossier_tp)
sortie = "téléchargement OK" if os.system("wget -nv -nc http://cedric.cnam.fr/vertigo/Cours/RCP216/docs/" + archive_zip + " -P" + dossier_tp) == 0 else "problème avec le téléchargement des fichiers"
print(sortie)
else:
print("archive zip présente dans " + dossier_tp)
if not os.path.exists(fichier_csv):
os.system("unzip " + dossier_tp + archive_zip + " -d " + dossier_tp)
Création du graphe¶
node_fields = [
StructField("id", StringType(), True),
StructField("latitude", FloatType(), True),
StructField("longitude", FloatType(), True),
StructField("population", IntegerType(), True)
]
nodes = spark.read.csv("data/tp-chemins-centralites/transport-nodes.csv", header=True,
schema=StructType(node_fields))
rels = spark.read.csv("data/tp-chemins-centralites/transport-relationships.csv", header=True)
reversed_rels = (rels.withColumn("newSrc", rels.dst)
.withColumn("newDst", rels.src)
.drop("dst", "src")
.withColumnRenamed("newSrc", "src")
.withColumnRenamed("newDst", "dst")
.select("src", "dst", "relationship", "cost"))
relationships = rels.union(reversed_rels)
Vérifions quelques éléments, comme le nombre de nœuds et d’arêtes
nodes.count()
relationships.count()
Maintenant, on utilise la bibliothèque GraphFrame pour créer un objet graphe.
g = GraphFrame(nodes, relationships)
Visualisation simple du graphe¶
Nous allons utiliser la bibliothèque Networkx pour visualiser ce graphe. Nous l’installons d’abord, puis on l’importe, avec Matplotlib. Nous étudierons la visualisation de graphes de façon approfondie dans un chapitre ultérieur.
import sys
!{sys.executable} -m pip install networkx
import networkx as nx
import matplotlib.pyplot as plt
On se dote d’une fonction qui automatise un peu la transformation de l’objet GraphFrames en un objet Networkx, pour la visualisation. En utilisant la documentation de Networkx, vous pouvez évidemment changer divers paramètres (couleurs des nœuds, des liens, étiquettes, etc.).
def PlotGraph(edge_list):
Gplot=nx.Graph()
for row in edge_list.select('src','dst').take(1000):
Gplot.add_edge(row['src'],row['dst'])
nx.draw(Gplot, with_labels=True, font_weight='bold')
PlotGraph(g.edges)
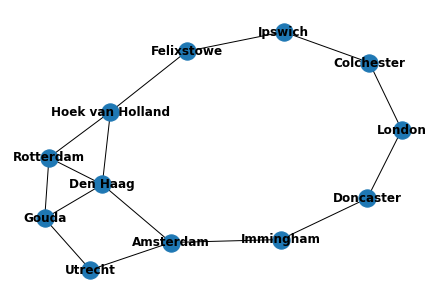
Fig. 95 Le graphe des villes¶
Chemins¶
Comme nous l’avons vu en cours, il existe plusieurs algorithmes pour parcourir des graphes. C’est une étape d’exploration souvent indispensable, un préalable à l’analyse. On cherche à trouver (et comprendre) quels sont les liens entre les nœuds dans le graphe, quelles sont les voies les plus rapides pour aller d’un nœud à un autre, etc.
Parcours en largeur (Breadth-First Search)¶
Nous allons trouver les villes de tailles comprises entre 100 000 et 300 000 habitants, dans nos données.
g.vertices.filter("population > 100000 and population < 300000").sort("population").show()
Nous allons maintenant trouver le plus court chemin entre Den Haag (La Haye) et une ville de taille moyenne (définie par le nombres d’habitants dans un intervalle) :
from_expr = "id='Den Haag'"
to_expr = "population > 100000 and population < 300000 and id <> 'Den Haag'"
result = g.bfs(from_expr, to_expr)
result.show()
Dans result, il y a des colonnes représentant des arêtes (commençant
par ‘e’) et d’autres représentant des sommets (commençant par ‘v’) On
filtre les arêtes, puis on affiche les nœuds :
columns = [column for column in result.columns if not column.startswith("e")]
result.select(columns).show(truncate=False)
Question :
Qu’observez-vous ? Pourquoi seulement Ipswich apparaît ?
Correction
Réponse : L’algo BFS s’arrête dès qu’un résultat satisfaisant est obtenu et, compte tenu des positions dans le graphe, Ipswich est évaluée avant Colchester, qui n’est donc pas présent dans le résultat fourni.
Parcours en profondeur (Depth-First Search)¶
Il ne semble pas y avoir pour le moment d’implémentation de DFS dans
graphframes. Il faut sans doute passer par la bibliothèque Pregel, qui
n’est pas disponible sur notre plateforme.
Plus court chemin¶
Avec le BFS, nous savons trouver le plus court chemin entre deux nœuds dans le graphe, en fonction du nombre de villes (nœuds) traversés. Nous souhaitons maintenant trouver le plus court chemin valué, c’est-à-dire en tenant compte des distances entre villes. Il nous faut cette fois utiliser une propriété “cost” présente dans les données.
On doit se doter d’une fonction user-defined (udf), et on écrit une fonction de calcul du plus court chemin en utilisant le passage de messages entre nœuds.
from graphframes.lib import AggregateMessages as AM
from pyspark.sql import functions as F
add_path_udf = F.udf(lambda path, id: path + [id], ArrayType(StringType()))
def shortest_path(g, origin, destination, column_name="cost"):
if g.vertices.filter(g.vertices.id == destination).count() == 0:
return (spark.createDataFrame(sc.emptyRDD(), g.vertices.schema)
.withColumn("path", F.array()))
vertices = (g.vertices.withColumn("visited", F.lit(False))
.withColumn("distance", F.when(g.vertices["id"] == origin, 0)
.otherwise(float("inf")))
.withColumn("path", F.array()))
cached_vertices = AM.getCachedDataFrame(vertices)
g2 = GraphFrame(cached_vertices, g.edges)
while g2.vertices.filter('visited == False').first():
current_node_id = g2.vertices.filter('visited == False').sort("distance").first().id
msg_distance = AM.edge[column_name] + AM.src['distance']
msg_path = add_path_udf(AM.src["path"], AM.src["id"])
msg_for_dst = F.when(AM.src['id'] == current_node_id, F.struct(msg_distance, msg_path))
new_distances = g2.aggregateMessages(F.min(AM.msg).alias("aggMess"),
sendToDst=msg_for_dst)
new_visited_col = F.when(
g2.vertices.visited | (g2.vertices.id == current_node_id), True).otherwise(False)
new_distance_col = F.when(new_distances["aggMess"].isNotNull() &
(new_distances.aggMess["col1"] < g2.vertices.distance),
new_distances.aggMess["col1"]) \
.otherwise(g2.vertices.distance)
new_path_col = F.when(new_distances["aggMess"].isNotNull() &
(new_distances.aggMess["col1"] < g2.vertices.distance),
new_distances.aggMess["col2"].cast("array<string>")) \
.otherwise(g2.vertices.path)
new_vertices = (g2.vertices.join(new_distances, on="id", how="left_outer")
.drop(new_distances["id"])
.withColumn("visited", new_visited_col)
.withColumn("newDistance", new_distance_col)
.withColumn("newPath", new_path_col)
.drop("aggMess", "distance", "path")
.withColumnRenamed('newDistance', 'distance')
.withColumnRenamed('newPath', 'path'))
cached_new_vertices = AM.getCachedDataFrame(new_vertices)
g2 = GraphFrame(cached_new_vertices, g2.edges)
if g2.vertices.filter(g2.vertices.id == destination).first().visited:
return (g2.vertices.filter(g2.vertices.id == destination)
.withColumn("newPath", add_path_udf("path", "id"))
.drop("visited", "path")
.withColumnRenamed("newPath", "path"))
return (spark.createDataFrame(sc.emptyRDD(), g.vertices.schema)
.withColumn("path", F.array()))
On peut maintenant utiliser notre fonction :
result = shortest_path(g, "Amsterdam", "Colchester", "cost")
result.select("id", "distance", "path").show(truncate=False)
Exercice :
Écrivez le code pour trouver le plus court chemin en termes de nœuds entre Amsterdam et Colchester (cf BFS supra), et comparez ce que vous obtenez.
Correction
from_expr = "id='Amsterdam'"
to_expr = "id='Colchester'"
result_nv = g.bfs(from_expr, to_expr)
columns = [column for column in result_nv.columns if not column.startswith("e")]
result_nv.select(columns).show(truncate=False)
rels.show()
Dans ce cas le chemin le plus court n’est pas celui qui traverse le moins de villes.
Centralités¶
Les centralités, ce sont des indicateurs qui permettent de trouver (et d’ordonner) les nœuds du graphe en fonction de leur importance. Bien entendu, chaque centralité met en avant certains nœuds au détriment d’autres, en fonction d’une formule. Nous allons en examiner plusieurs, de la plus évidente (centralité de degré) à des plus complexes (comme la centralité de proximité ou le PageRank).
Tout en conservant l’usage du graphe de transport présenté dans la première partie, nous allons utiliser un nouveau graphe, reposant sur un réseau social.
Chargement des données, statistiques élémentaires¶
social_v = spark.read.csv("data/tp-chemins-centralites/social-nodes.csv", header=True)
social_e = spark.read.csv("data/tp-chemins-centralites/social-relationships.csv", header=True)
social_g = GraphFrame(social_v, social_e)
social_e.show()
social_v.show()
Visualisation du graphe¶
labels = {}
for row in social_e.select('src','dst','relationship').take(1000):
labels[(row['src'],row['dst'])]=row['relationship']
G = nx.Graph()
for row in social_e.select('src','dst').take(1000):
G.add_edge(row['src'],row['dst'])
pos = nx.spring_layout(G,k=1.9)
plt.figure()
nx.draw(
G, pos, with_labels=True, edge_color='black', width=1, linewidths=1,
node_size=500, node_color='pink', alpha=0.9,
labels={node: node for node in G.nodes()}
)
nx.draw_networkx_edge_labels(
G, pos,
edge_labels=labels,
font_color='blue'
)
plt.axis('off')
plt.show()
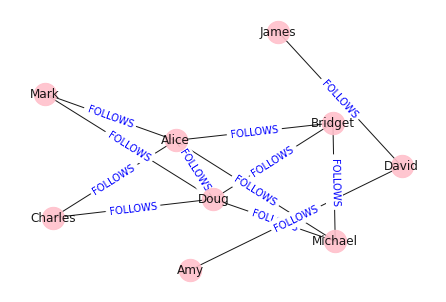
Fig. 96 Le graphe social. Attention, les arêtes ne sont pas orientées sur la figure !¶
Centralité de Degré¶
La centralité de degré consiste à ordonner les nœuds en fonction de leur degré, c’est-à-dire du nombre d’autres nœuds qui leur sont liés. On considère éventuellement des degrés entrants et sortants (out-degree) dans un contexte de graphe dirigé.
Pour le graphe de transport¶
total_degree = g.degrees
in_degree = g.inDegrees
out_degree = g.outDegrees
(total_degree.join(in_degree, "id", how="left")
.join(out_degree, "id", how="left")
.fillna(0)
.sort("inDegree", ascending=False)
.show())
Centralité de Proximité¶
On réutilise des fonctions utilisées précédemment, et on les étend, pour calculer la centralité de proximité.
from graphframes.lib import AggregateMessages as AM
from pyspark.sql import functions as F
from pyspark.sql.types import *
from operator import itemgetter
def collect_paths(paths):
return F.collect_set(paths)
collect_paths_udf = F.udf(collect_paths, ArrayType(StringType()))
paths_type = ArrayType(
StructType([StructField("id", StringType()), StructField("distance", IntegerType())]))
def flatten(ids):
flat_list = [item for sublist in ids for item in sublist]
return list(dict(sorted(flat_list, key=itemgetter(0))).items())
flatten_udf = F.udf(flatten, paths_type)
def new_paths(paths, id):
paths = [{"id": col1, "distance": col2 + 1} for col1, col2 in paths if col1 != id]
paths.append({"id": id, "distance": 1})
return paths
new_paths_udf = F.udf(new_paths, paths_type)
def merge_paths(ids, new_ids, id):
joined_ids = ids + (new_ids if new_ids else [])
merged_ids = [(col1, col2) for col1, col2 in joined_ids if col1 != id]
best_ids = dict(sorted(merged_ids, key=itemgetter(1), reverse=True))
return [{"id": col1, "distance": col2} for col1, col2 in best_ids.items()]
merge_paths_udf = F.udf(merge_paths, paths_type)
def calculate_closeness(ids):
nodes = len(ids)
total_distance = sum([col2 for col1, col2 in ids])
return 0 if total_distance == 0 else nodes * 1.0 / total_distance
closeness_udf = F.udf(calculate_closeness, DoubleType())
Pour le graphe de transport¶
vertices = g.vertices.withColumn("ids", F.array())
cached_vertices = AM.getCachedDataFrame(vertices)
g2 = GraphFrame(cached_vertices, g.edges)
for i in range(0, g2.vertices.count()):
msg_dst = new_paths_udf(AM.src["ids"], AM.src["id"])
msg_src = new_paths_udf(AM.dst["ids"], AM.dst["id"])
agg = g2.aggregateMessages(F.collect_set(AM.msg).alias("agg"),
sendToSrc=msg_src, sendToDst=msg_dst)
res = agg.withColumn("newIds", flatten_udf("agg")).drop("agg")
new_vertices = (g2.vertices.join(res, on="id", how="left_outer")
.withColumn("mergedIds", merge_paths_udf("ids", "newIds", "id"))
.drop("ids", "newIds")
.withColumnRenamed("mergedIds", "ids"))
cached_new_vertices = AM.getCachedDataFrame(new_vertices)
g2 = GraphFrame(cached_new_vertices, g2.edges)
(g2.vertices
.withColumn("closeness", closeness_udf("ids"))
.sort("closeness", ascending=False).select('id','closeness')
.show(truncate=False))
Question :
Qu’observez-vous ?
Exercice :
Refaites et commentez le résultat de la centralité de proximité pour le graphe social.
Correction
social_v = social_g.vertices.withColumn("ids", F.array())
cached_social_vertices = AM.getCachedDataFrame(social_v)
social_g2 = GraphFrame(cached_social_vertices, social_g.edges)
for i in range(0, social_g2.vertices.count()):
social_msg_dst = new_paths_udf(AM.src["ids"], AM.src["id"])
social_msg_src = new_paths_udf(AM.dst["ids"], AM.dst["id"])
agg = social_g2.aggregateMessages(F.collect_set(AM.msg).alias("agg"),
sendToSrc=social_msg_src, sendToDst=social_msg_dst)
res = agg.withColumn("newIds", flatten_udf("agg")).drop("agg")
social_new_vertices = (social_g2.vertices.join(res, on="id", how="left_outer")
.withColumn("mergedIds", merge_paths_udf("ids", "newIds", "id"))
.drop("ids", "newIds")
.withColumnRenamed("mergedIds", "ids"))
social_cached_new_vertices = AM.getCachedDataFrame(social_new_vertices)
social_g2 = GraphFrame(social_cached_new_vertices, social_g2.edges)
(social_g2.vertices
.withColumn("closeness", closeness_udf("ids"))
.sort("closeness", ascending=False).select('id','closeness')
.show(truncate=False))
[une solution plus rapide est de remplacer seulement g par social_g dans le code pour le graphe de transport, sans changer les autres noms]
Centralité d’intermédiarité¶
La centralité d’intermédiarité n’est pas implémentée en standard dans Apache Spark. Il devrait cependant être possible d’écrire du code permettant de la calculer. Ceci est pour le moment laissé en exercice pour le lecteur très motivé.
PageRank¶
Le PageRank est la centralité la plus connue, inventée et popularisée par Larry Page, le créateur de Google, dont l’algorithme utilise la mesure pour classer des pages Web. Il y a deux approches pour l’utiliser dans Spark (pas besoin de coder ce calcul), avec un nombre d’itérations fixé ou jusqu’à une convergence.
Approche avec nombre d’itérations fixé¶
results = g.pageRank(resetProbability=0.15, maxIter=20)
results.vertices.sort("pagerank", ascending=False).show()
social_results = social_g.pageRank(resetProbability=0.15, maxIter=20)
social_results.vertices.sort("pagerank", ascending=False).show()
Approche « jusqu’à convergence »¶
results2 = g.pageRank(resetProbability=0.15, tol=0.01)
results2.vertices.sort("pagerank", ascending=False).show()
social_results2 = social_g.pageRank(resetProbability=0.15, tol=0.01)
social_results2.vertices.sort("pagerank", ascending=False).show()
Question :
Dans quel cas pensez-vous qu’il soit préférable d’utiliser l’approche avec nombre d’itérations fixé ?
PageRank personalisé¶
Le PageRank personnalisé (PPR pour Personalized PageRank) calcule
l’importance des nœuds dans un graphe par rapport à un ensemble de
nœuds initial (éventuellement composé d’un seul nœud). Les sauts sont
biaisés vers cet ensemble, ce qui permet à cet algorithme de proposer,
par exemple, des recommandations efficaces. Nous l’utilisons ici pour
voir quels autres nœuds l’utilisateur Doug devrait suivre.
me = "Doug"
social_ppr_results = social_g.pageRank(resetProbability=0.15, maxIter=20, sourceId=me)
people_to_follow = social_ppr_results.vertices.sort("pagerank", ascending=False)
already_follows = list(social_g.edges.filter(f"src = '{me}'").toPandas()["dst"])
people_to_exclude = already_follows + [me]
people_to_follow[~people_to_follow.id.isin(people_to_exclude)].show()
Question :
Revenez à la structure (la visualisation étant ambigue) du graphe ci-dessus et indiquez ce que vous pensez du résultat de ce calcul.
Question bonus :
Refaites ce calcul à partir d’un autre nœud, ou sur le graphe de transport, et observez les changements.
Correction
me = "Alice"
social_ppr_results = social_g.pageRank(resetProbability=0.15, maxIter=20, sourceId=me)
people_to_follow = social_ppr_results.vertices.sort("pagerank", ascending=False)
already_follows = list(social_g.edges.filter(f"src = '{me}'").toPandas()["dst"])
people_to_exclude = already_follows + [me]
people_to_follow[~people_to_follow.id.isin(people_to_exclude)].show()
Références¶
Ce notebook a été adapté à partir du livre “Graph Algorithms: Practical Examples in Apache Spark and Neo4j”, de Mark Needham et Amy E. Hodler.

