Cours - Fouille de graphes et réseaux sociaux¶
Format des séances et supports
Ce chapitre est dispensé sur 2 séances. Vous pouvez cependant télécharger les diapositives (1 par page) des 2 séances :
première séance, Introduction et méthodologie [pdf]
deuxième séance, Modélisation et propriétés des graphes [pdf]
Introduction¶
Un réseau social est un ensemble d’individus qui interagissent. L’étude scientifique de ces groupes a débuté dans les années 50, avec les travaux des anthropologues J.A. Barnes, M. Gluckman suivis par le sociologue M. Granovetter [G73].
Une des premières expériences est celle de S. Milgram [M67], un psychologue américain, appelée « l’expérience des six degrés de séparation » (1967). Elle vise à étudier les degrés qui séparent des individus, donc les interconnexions entre leurs réseaux sociaux. L’objectif de l’expérience : faire transiter une lettre depuis Omaha (Nebraska) jusqu’à Boston (Massachussetts). Plusieurs expériences ont été menées. Dans l’une de celles-ci, 296 lettres partent d’Omaha (remise entre les mains de volontaires), qui doivent les faire parvenir à une personne donnée, résidant à Boston. Chacune des personnes qui reçoit la lettre doit la remettre en mains propres à une personne de son choix, supposée permettre de rapprocher la lettre de l’objectif.
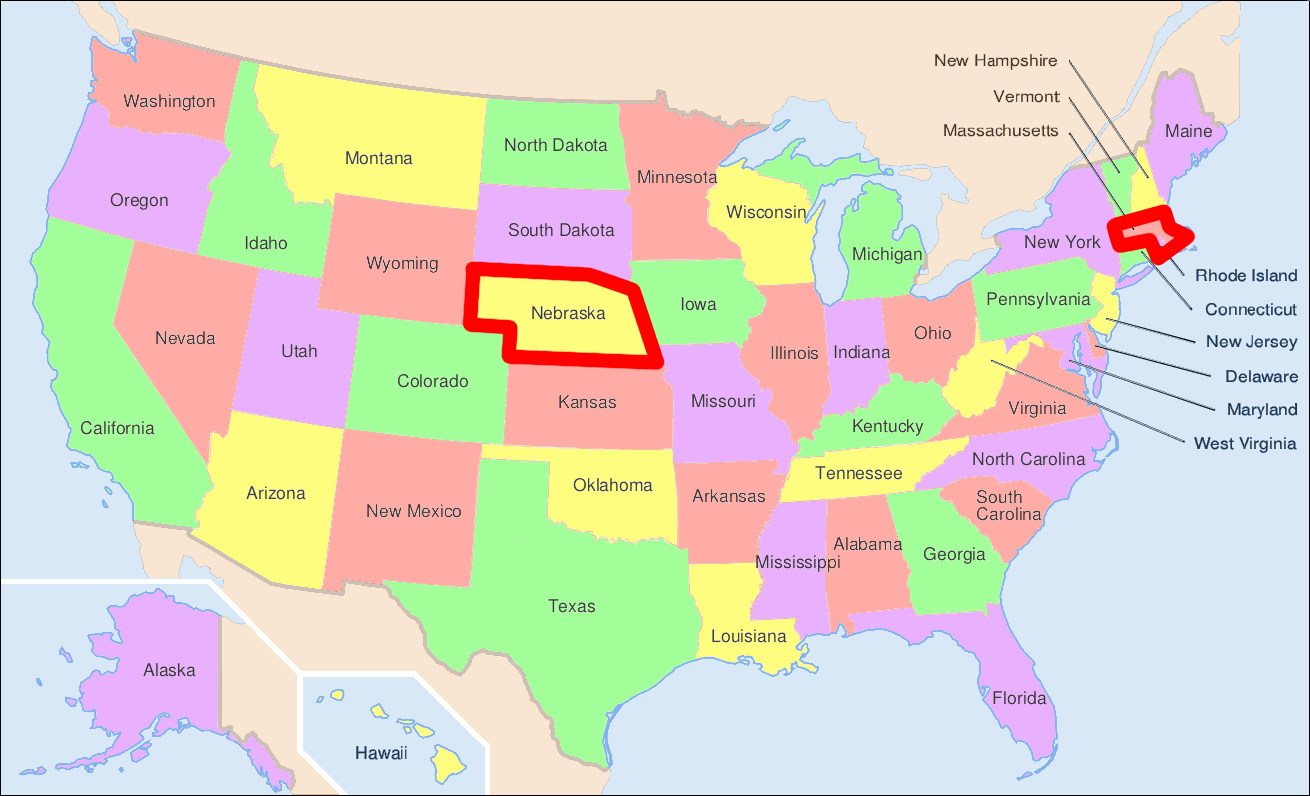
Fig. 84 Carte des USA avec les États de départ et d’arrivée des lettres de Milgram¶
Les résultats furent les suivants : 64 lettres sur 296 arrivèrent, et les chemins eurent en moyenne 5,2 intermédiaires, ce qui amena l’expression « six degrés de séparation ». Plusieurs observations ont été tirées de cette expérience, par Milgram lui-même ou d’autres depuis :
il existe des « chemins courts » entre des personnes lointaines (une lettre ne mit que 4 jours pour arriver). Ce phénomène, déjà postulé par F. Karinthy en 1929, s’appelle aussi « phénomène du petit monde » ;
les membres du réseau parviennent à trouver ces chemins sans connaissance exhaustive de l’organisation du réseau (qui est ici de taille très grande, avec 300 millions d’habitants aux USA) : leur connaissance essentiellement locale leur permet de trouver des chemins globaux ;
pour les lettres qui ne sont pas arrivées (232, tout de même), l’interruption de la chaîne ne veut pas nécessairement dire qu’il n’existait pas de chemin ;
les lettres arrivées nous permettent de connaître des chemins de longueur x, ce qui ne veut pas dire qu’il n’existait pas de chemin de longueur inférieure (mais seulement que la transmission ne l’a pas empruntée à ce moment-là).
Depuis 1967, cette expérience a été reproduite plusieurs fois, avec des conditions expérimentales différentes, avec des courriers électroniques notamment, mais aussi en 2011 par les chercheurs de Facebook. Les résultats sont sensiblement les mêmes, bien que la valeur moyenne de la longueur des chemins varie un peu (4,74 dans le cas de Facebook).
Une partie importante de ces travaux de recherche a consisté à proposer des modèles pour formaliser et reproduire l’expérience de Milgram sur des graphes aléatoires. En particulier, cela a conduit à développer des outils mathématiques dérivant de la théorie des graphes pour pouvoir analyser les phénomènes observés. D. Watts, associé à S. Strogatz, puis J. Kleinberg ont proposé des modélisations, reposant sur l’existence de distances connues localement et d’autres globalement.
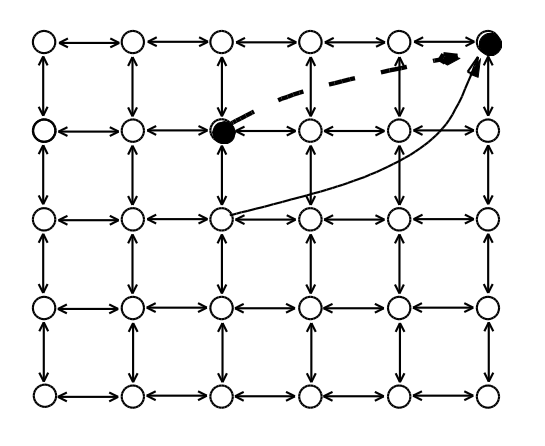
Le modèle de Kleinberg [K00] présente une grille, régulière, supposée connue de tous (connaissance globale). Les liens sont orientés, la connaissance des uns et des autres n’est pas forcément mutuelle. On ajoute \(q\) voisins quelconques à chaque sommet, pointant vers un nœud éloigné du réseau. Ces liens représentent les connaissances locales du nœud (il est le seul de son voisinage à connaître ces personnes éloignées). Ces liens sont distribués aléatoirement dans le réseau, en suivant une loi de probabilité proportionnelle à l’inverse de la distance entre les points (élevée à une puissance \(s\) à paramétrer) : \(p_{(u,v)} \propto \frac{1}{d^s}\).
On peut voir la grille comme une modélisation du réseau social géographiquement proche, les liens supplémentaires comme des relations éloignées. Un individu connaît quelques personnes loin de lui, et celles-ci ne sont pas connues des gens qui vivent dans la même ville que lui (exemple : sa famille éloignée, anciens collègues).
Les auteurs de l’expérience proposent de faire circuler les messages selon un algorithme glouton, c’est-à-dire ici qu’il choisira toujours le voisin le plus proche de la cible (en fonction d’une distance sur la grille).
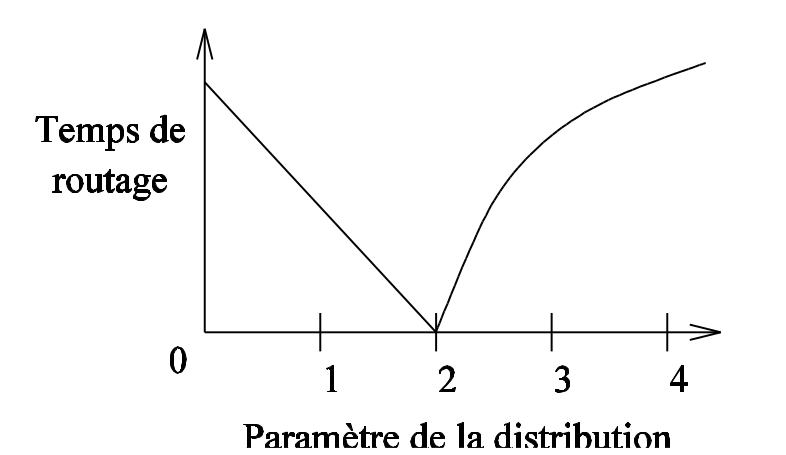
Fig. 85 Courbe de l’approximation du (log du) « temps » de routage en fonction de s¶
Le point surprenant de l’étude est l’effet de seuil observé sur la valeur de \(s\) : avec une valeur de \(s=2\), l’acheminement du message requiert en moyenne \(log(n)\) sauts. C’est la seule valeur pour laquelle cela se produit, avec des valeurs significativement supérieures dans les autres cas (\(n^{(2-s)/3}\) pour \(0 \leq s \lt 2\), \(n^{(s-2)/(s-1)}\) pour \(s>2\)). Voir la Fig. 85. En fait, quand s est trop petit, la probabilité de pointer sur des liens distants est forte : l’algorithme « saute » souvent à longue distance, même quand il est proche de la destination, rallongeant la marche. Avec s grand, les liens aléatoires ne permettent pas de faire de « grand saut » vers la destination, le chemin reste long.
Ce phénomène de « petit monde » a été généralisé ensuite à des réseaux de dimension \(d > 2\). Il a été aussi mis en évidence expérimentalement dans des réseaux variés, qu’il s’agisse des neurones de Caenorhabditis elegans ou de la distribution d’électricité aux USA.
Des exemples de réseaux sociaux et de graphes d’interaction¶
Depuis l’arrivée, au début des années 2000, de technologies ayant permis le Web 2.0 (participatif), les « réseaux sociaux en ligne » se sont multipliés. Il s’agit de l’informatisation de modélisations parfois existantes, qui a rendu visible (et grand public) la notion de « réseau social ». Les membres de ces plateformes peuvent interagir avec leur « réseau » : ajouter des amis (Facebook, LinkedIn), suivre des personnes (Twitter), créer des groupes.
Les réseaux sociaux constituent des réseaux d’interaction particuliers, entre individus. Examinons quelques exemples célèbres de tels réseaux.
Le nombre d’Erdős¶

Pál Erdős fut un mathématicien hongrois (1913-1996) extrêmement prolifique, qui co-signa des articles avec plus de 500 collaborateurs directs. Pour lui rendre hommage, le graphe des chercheurs en mathématiques a été étudié et chaque membre peut évoquer son « nombre d’Erdős », qui évalue la distance à Erdős dans ce graphe de collaboration. Le nombre d’Erdős est donc défini comme suit :
0 : Pál Erdős
1 : ses collaborateurs
2 : les collaborateurs de ses collaborateurs
etc.
Voir l’Erdős Number project sur http://www.oakland.edu/enp/.
En pratique : il suffit de récupérer une liste d’articles et de calculer les plus courts chemins entre chaque chercheur et Erdős. On pourrait bien sûr calculer en prenant un autre scientifique pour référence.
Le Kevin Bacon Game¶

Kevin Bacon (1958–) est acteur américain et le Kevin Bacon Game (ou « Six Degrees of Kevin Bacon ») est une transposition du concept de nombre d’Erdős à l’univers d’Hollywood. En 1994, sur un forum d’Internet, des étudiants se sont demandés (alors que des bases de données n’existaient pas encore) dans combien de films il avait joué et le nombre de personnes avec lesquelles il avait joué. Rapidement, c’est devenu un jeu pour cinéphiles que d’essayer de relier des acteurs au hasard avec Kevin Bacon. Deux acteurs sont reliés s’ils ont joué dans un même film.
Il existe maintenant une plateforme en ligne où l’on peut vérifier les résultats : http://oracleofbacon.org/. On peut également y calculer les distances entre acteurs (en dehors de Kevin Bacon) :
Distance entre Tom Cruise et Clint Eastwood ? 2 (un acteur commun entre Space Cowboys et Eyes Wide Shut)
Distance entre Mickey Mouse et Omar Sy ? 4
Il existe quelques acteurs qui ne peuvent pas être reliés à Kevin Bacon.
Réseaux de connaissances professionnelles¶
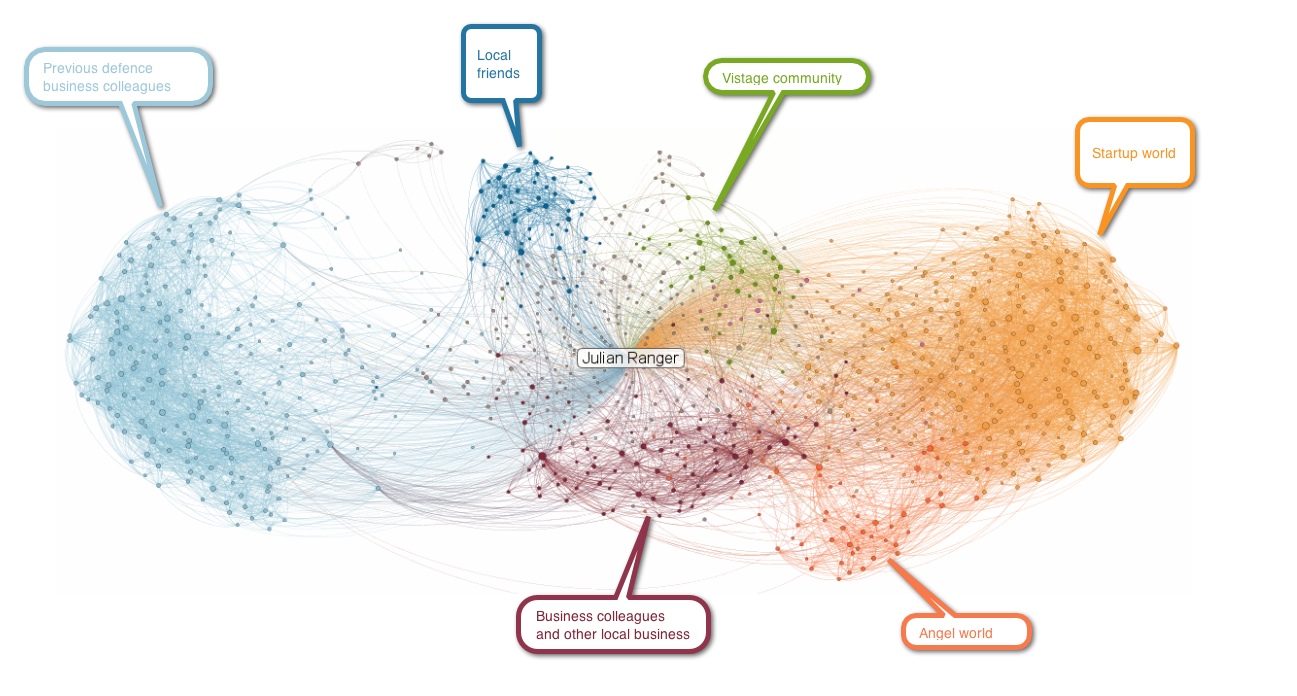
Fig. 86 Réseau professionnel égocentré¶
Réseaux de communication¶
Les communications entre individus requièrent des réseaux de communication (réseau téléphonique, Internet, etc.). On peut collecter et analyser les échanges par le biais de ces réseaux. Internet n’est pas constitué que du Web, d’autres protocoles y existent : mail (SMTP/POP/IMAP), réseaux peer-to-peer (BitTorrent, Gnutella, etc.).
En 2011, Friggeri et Latapy ont par exemple observé la diffusion d’un fichier de proche en proche dans un réseau P2P. Comme on le verra plus tard, étudier Internet pose un certain nombre de questions (biais de mesure), même si cela fournit souvent des données nombreuses et extrêmement riches.
Le projet Senseable (http://senseable.mit.edu/realtimerome/) a collecté diverses informations sur le réseau téléphonique et présenté des analyses (type d’appelant, comportement de mobilité), durant la finale de la coupe du monde de football en 2006 :
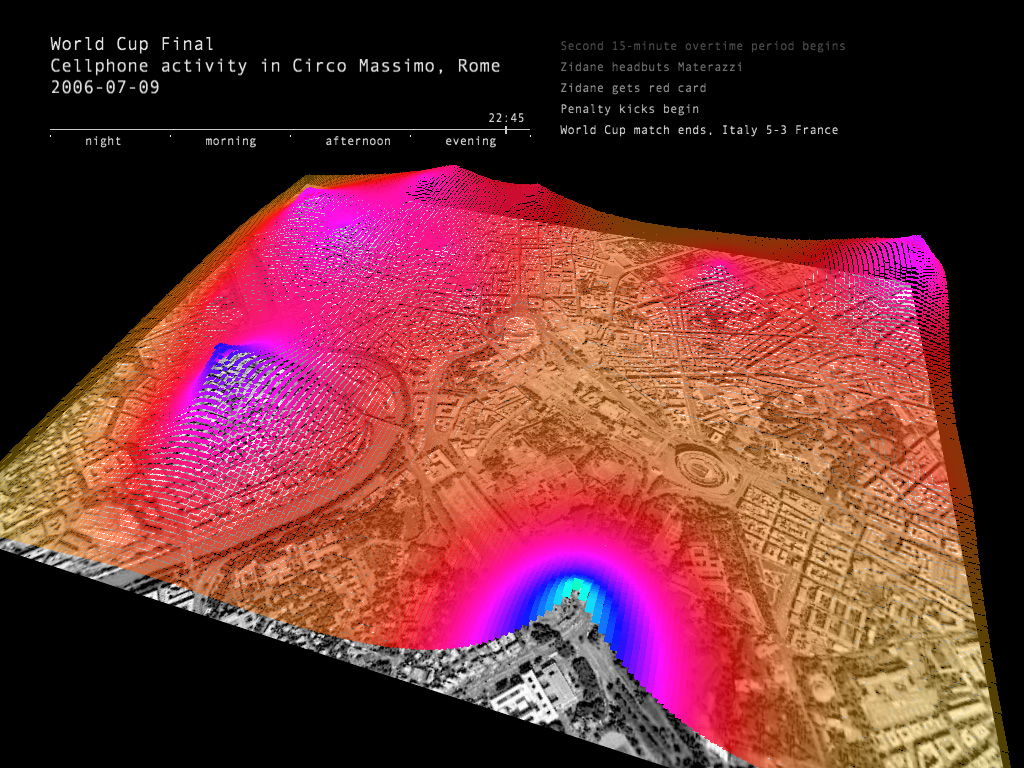
Encore d’autres réseaux¶
D’autres réseaux présentent des caractéristiques communes et soulèvent des problématiques d’études similaires :
informatique : pages Web, routeurs, P2P, etc.
biologie : protéines, neurones cérébraux, etc.
sciences sociales : amitiés, collaboration, contacts sexuels, etc.
économie : échanges financiers
histoire : mariages
linguistique : synonymie, co-occurrence
transports : réseau aérien, électrique
Éléments de théorie des graphes¶
En vue de permettre l’étude des graphes et réseaux sociaux, nous rappelons ici quelques définitions et de la terminologie issue de la théorie des graphes.
Un graphe est défini par un couple \(G = (V,E)\) tel que :
\(V\) (pour l’anglais vertices) est un ensemble fini de sommets
\(E\) (pour l’anglais edges) est un ensemble fini de arêtes
Un graphe peut être orienté, ou non :
si oui, les couples \((v_i, v_j) \in E\) sont ordonnés, \(v_i\) est le sommet initial, \(v_j\) est le sommet terminal. on appelle alors le couple \((v_i, v_j)\) un arc, représenté graphiquement par \(v_i \rightarrow v_j\).
si non, les couples ne sont pas orientés et \((v_i, v_j)\) est équivalent à \((v_j, v_i)\), et on l’appelle arête, représenté par \(v_i - v_j\).
Terminologie :
l’ordre d’un graphe, c’est son nombre de sommets (souvent désigné par \(n\)) ;
une boucle est un arc/une arête reliant un sommet à lui-même ;
un graphe dépourvu de boucles est dit élémentaire ;
un graphe simple ne comporte pas de boucles et au plus une arête entre deux sommets ;
un graphe partiel est le graphe obtenu en supprimant certains arcs ou arêtes ;
un sous-graphe est le graphe obtenu en supprimant certains sommets et tous les arcs/arêtes incidents aux sommets supprimés ;
un graphe est dit complet s’il comporte une arête \((v_i, v_j)\) pour toute paire de sommets \((v_i, v_j) \in E^2\) ;
un sommet \(v_i\) est dit adjacent à un autre s’il existe une arête entre eux (on parle alors de sommets voisins) ;
le degré d’un sommet est le nombre d’arêtes incidentes à ce sommet (il peut y avoir un degré entrant et un degré sortant, pour les graphes orientés) ;
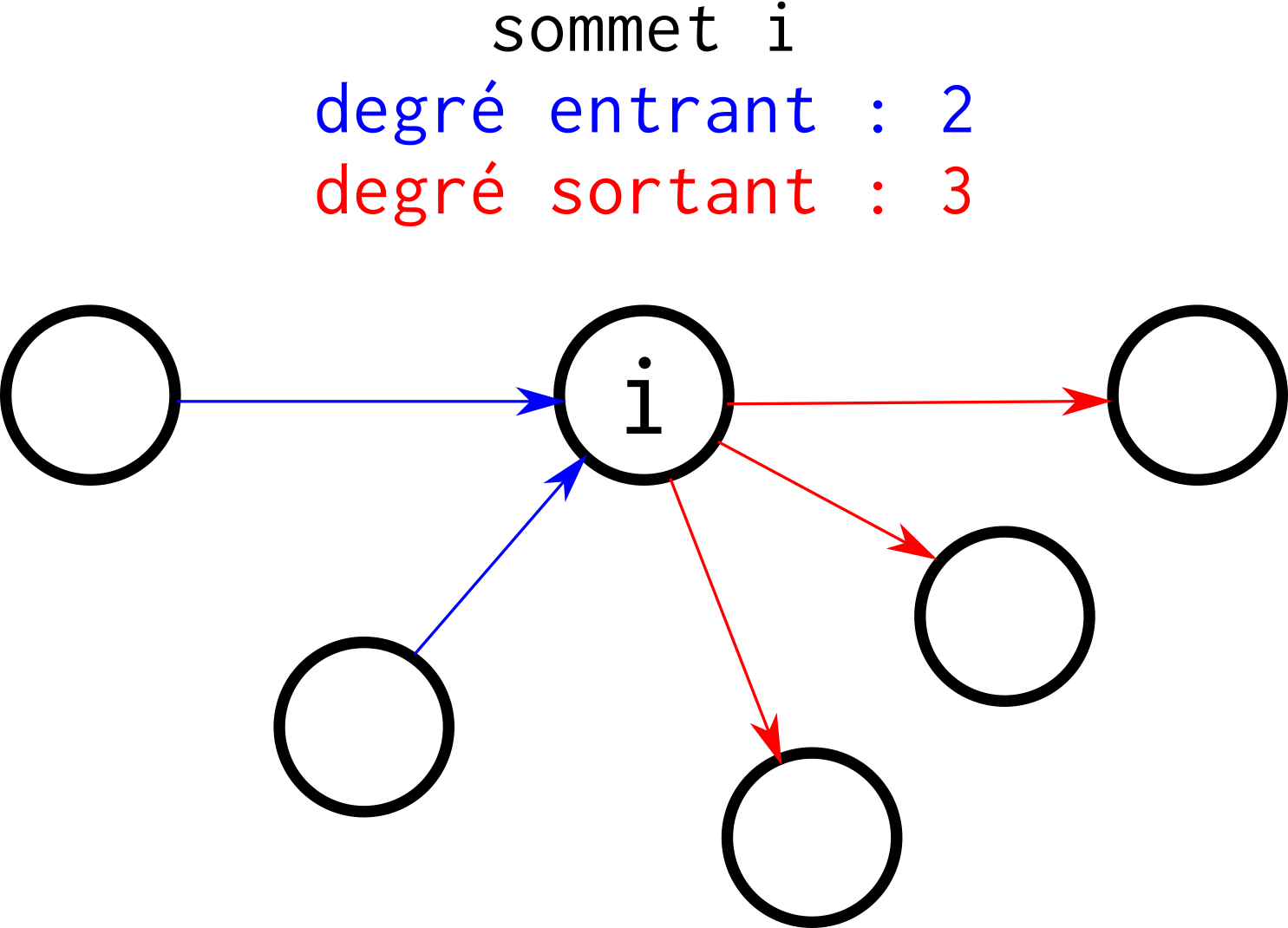
Fig. 87 Degré entrant, degré sortant. Si les liens de ce graphe n’étaient pas orientés, le degré de i serait de 5.¶
le plus court chemin entre deux nœuds est la valeur qui minimise la somme des valuations des arêtes empruntées pour parcourir le chemin entre ces nœuds. Dans un graphe non valué, il s’agit simplement du plus petit nombre d’arêtes à emprunter pour passer d’un nœud à l’autre. L’algorithme de Dijkstra permet de calculer le plus court chemin entre deux nœuds avec une complexité polynomiale (non détaillé ici, voir par exemple l’article Wikipedia consacré) ;
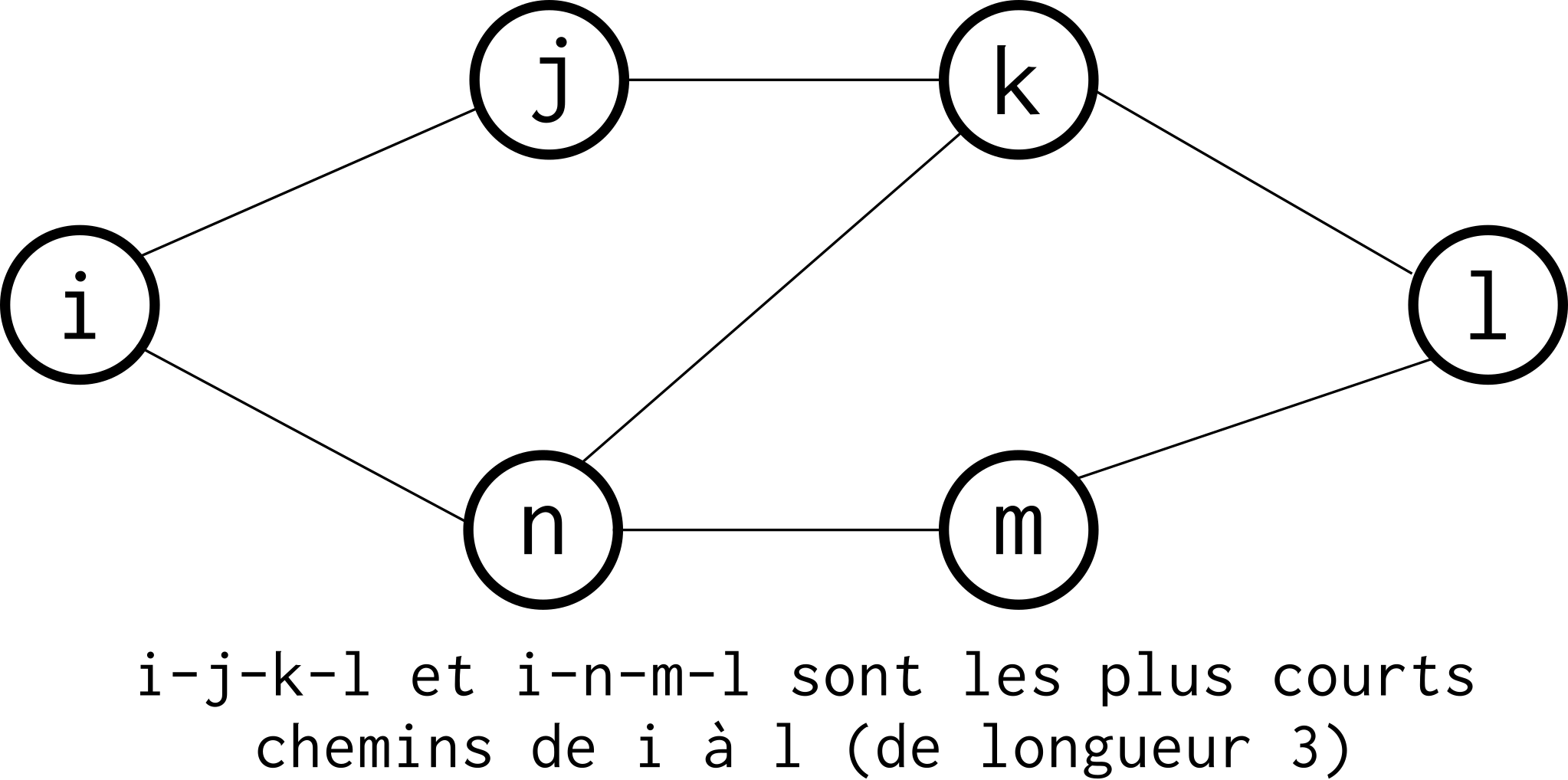
Fig. 88 Entre les noeuds i et l, il y a trois plus courts chemins : i-j-k-l, i-n-m-l et i-n-k-l. Ils ont pour longueur 3.¶
l”excentricité d’un nœud d’un graphe est la distance maximale entre le nœud et les autres nœuds du graphe. Pour l’obtenir, on calcule le plus court chemin avec chaque autre nœud et on garde le maximum ;
le diamètre d’un graphe (ou excentricité maximale) est la valeur maximale des distances entre les nœuds. Le rayon du graphe est son excentricité minimale ;
le centre d’un graphe est le nœud d’excentricité minimale (c’est à dire le nœud dont la distance maximale aux autres est la plus faible) ; une même valeur d’excentricité minimale peut être obtenue pour plusieurs nœuds, tous ces nœuds sont alors des centres du graphes.
Étudier de tels réseaux¶
L’objectif est de comprendre le comportement des entités qui interagissent dans le système étudié, les lois qui les gouvernent. On cherche donc :
quelle est la structure des graphes ?
quelle est l’évolution de cette structure ?
quels sont les phénomènes reposant sur l’existence de ce réseau ?
Les applications sont multiples. En informatique et élécommunications, comme la conception et la mise en place de réseaux est un enjeu crucial, on étudie les réseaux existants en vue de les améliorer (en amendant les protocoles existants ou en élaborant de nouveaux), que ce soit pour des questions de performances ou de sécurité. En sciences humaines, l’étude de réseaux d’interaction permet de comprendre la diffusion d’innovations (économie), de rumeurs (sociologie). En médecine, les réseaux sont fondamentaux pour comprendre les interactions entre protéines mais aussi la propagation de virus au sein des populations (et les effets des campagnes de vaccination, par exemple).
On propose dans ce cours une méthode d’étude générale, qui est ensuite affinée par les praticiens des différentes disciplines en fonction de leurs besoins. Les outils sont souvent les mêmes :
Théorie des graphes
Analyse statistique
Modélisation probabiliste
On procède parfois à de la simulation sur des données synthétiques que l’on compare à des données réelles.
Les problématiques rencontrées dans l’étude des réseaux sociaux peuvent être classées en quatre catégories : Mesure, Modélisation, Analyse et Algorithmique. Il faudra souvent faire des allers-retours entre ces domaines, par exemple en améliorant le modèle après des analyses préliminaires peu satisfaisantes, voir refaire une expérience de captation de données.
Mesure¶
La mesure, ou métrologie, désigne ici la capture des données. Les réseaux sociaux que l’on cherche à étudier sont généralement issus d’une expérience de mesure d’un système donné, vu comme un graphe. Celle-ci est particulièrement déterminante : une mauvaise capture peut rendre complètement fausses les analyses subséquentes. Il faut donc, dès l’obtention des données, se poser la question des « biais d’observation », en ayant des réponses précises aux questions suivantes :
quelle proportion du système a été mesurée ?
combien de temps la mesure a-t-elle duré ?
quelles étaient les contraintes techniques ?
qui a fait la mesure ?
la mesure peut-elle être reproduite ?
Compte tenu de la taille des systèmes concernés (Facebook et Twitter/X comptent plusieurs centaines de millions d’utilisateurs), de leur caractère dynamique (les réseaux P2P ont des utilisateurs qui ne restent dans le système que quelques heures au maximum), ces problématiques jouent fortement sur la qualité des représentations qui seront obtenues. En effet, un graphe qui ne modéliserait que 1000 utilisateurs de Facebook, par exemple, ne pourrait évidemment prétendre décrire le comportement global des membres de cette plateforme. De même, une mesure d’une heure sur un réseau P2P très populaire ne mènera qu’à des analyses limitées. Enfin, la connaissance du protocole de mesure est importante pour estimer si des informations observables n’ont pas été observées.
Par exemple, l’utilisation de l’outil traceroute, souvent employé pour établir des « cartes physiques » de l’Internet, présente un certain nombre de caractéristiques qu’il faut maîtriser. Cet outil enregistre les chemins qu’empruntent des paquets de données pour atteindre une adresse IP spécifique, à partir d’une source. Ces deux paramètres, une adresse IP de départ et une d’arrivée, sont des contraintes fortes sur la mesure, et on doit en tenir compte : pour cartographier une zone de l’Internet (par exemple, l’environnement d’une machine donnée), il est donc nécessaire de multiplier les points « source » à partir desquels on tentera d’atteindre cette machine. Il faut noter que certaines zones seront inaccessibles (par exemple des routeurs de degré 1, sauf s’ils sont sources ou destinations), et que la répartition de charge (load-balancing) peut amener des routeurs en milieu de chemin à faire passer les paquets par une branche d’une fourche plutôt qu’une autre (cf Fig. 89 et Fig. 90). Ces deux phénomènes conduisent à ne pas observer certains nœuds et certains liens du réseau, ce qui peut changer considérablement les caractéristiques du réseau mesuré par rapport au réseau original (cf Fig. 91, où la distribution de degrés observée n’est pas la même que celle qu’on attendrait : il y a des contraintes techniques qui ont un impact significatif sur la mesure).
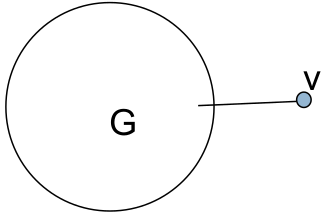
Fig. 89 Nœud accessible par un seul chemin¶
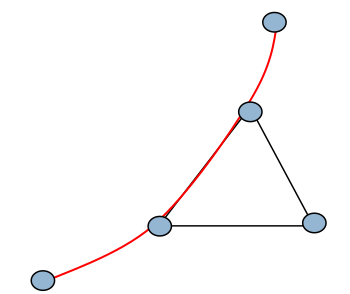
Fig. 90 Équilibrage de charge sur une fourche¶
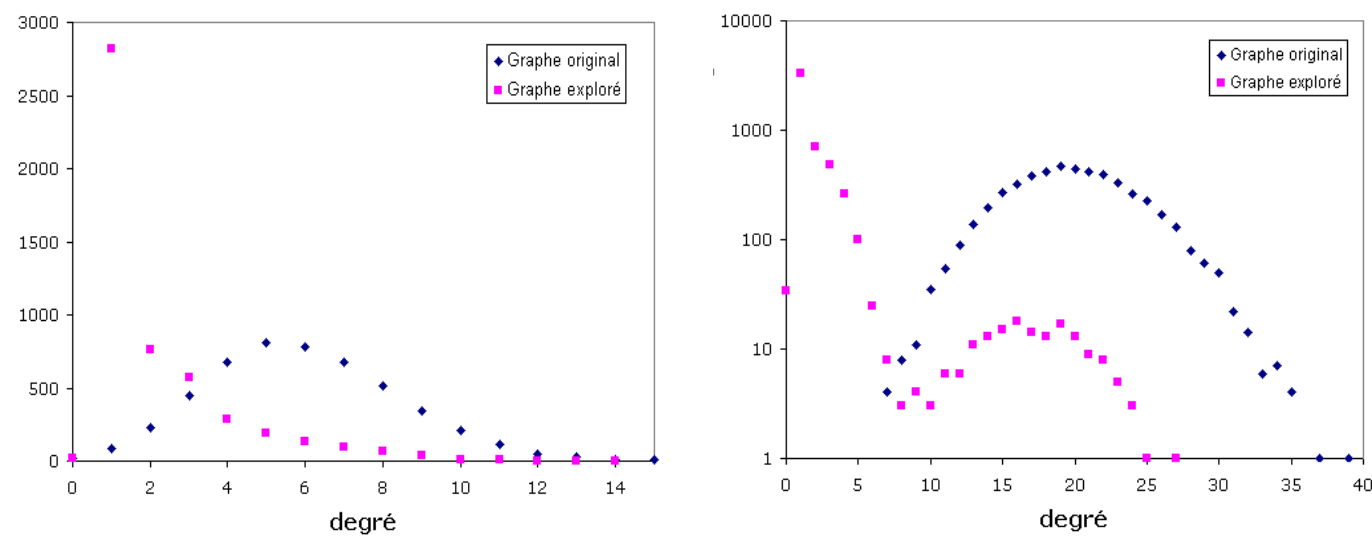
Fig. 91 Distribution de degrés observée et distribution réelle¶
Analyse¶
Une fois que les données sont collectées, il faut procéder à l’analyse de celles-ci. L’objectif est d’obtenir des informations pertinentes sur le système, à l’aide d’une description statistique que l’on interprète ensuite. L’analyse des graphes peut passer d’abord par la détermination des valeurs de certaines propriétés « classiques » (distribution de degrés, longueurs des chemins, etc.), ou des propriétés spécifiques pertinentes pour le graphe en question (coefficient de clustering, existence et taille de communautés, etc.). L’analyse peut aussi requérir une phase préalable de modélisation (cf Modélisation), permettant de comparer le graphe étudié avec un ou des graphes aléatoires « similaires » (ou supposés tels). Enfin, un aspect important mais sur lequel on s’étend peu dans ce cours, c’est l’évolution dynamique des graphes : quels sont les changements des valeurs des propriétés au cours du temps.
Quelques propriétés classiques¶
Les propriétés classiques que l’on peut observer sur des graphes proviennent de la théorie des graphes.
la longueur moyenne des plus courts chemins : on la définit comme la moyenne, pour toutes les paires de sommets du graphe, des plus courts chemins. Formellement, pour un graphe \(G(V,E)\) où \(d(v_1,v_2)\) désigne le plus court chemin entre \(v_1\) et \(v_2\) (\(v_1,v_2 \in V\)), la longueur moyenne \(l_G\) vaut : \(l_G = \frac{1}{n(n-1)} \sum_{i \neq j} d(v_1,v_2)\).
le coefficient de clustering. Il existe une version globale, parfois appelée « transitivité », et une version locale, provenant du travail de Watts et Strogatz [WS98].
La version globale est définie comme : \(C = \frac{3 \times \text{nb triangles}}{\text{nb triplets connectés}}\). Un triplet connecté étant soit un triangle (triplet fermé), soit un triangle privé d’une arête (triplet ouvert).
Notons \(N(i)\) le voisinage du sommet i : \(N(i) = \{ v_j : e_{ij} \in E\}\) (ensemble des sommets connectés à i par au moins une arête). Cette version locale mesure, pour un sommet donné, à quel point son voisinage se rapproche d’une clique, qui est un ensemble de \(|N(i)|+1\) sommets tous connectés entre eux. On définit le coefficient de clustering comme étant le rapport entre le nombre d’arêtes existant dans le voisinage et le nombre de celles qu’il pourrait y avoir s’il s’agissait d’une clique. Pour un sommet avec \(k_i\) voisins, il pourrait y avoir \(\frac{k_i(k_i-1)}{2}\) arêtes. Donc, la valeur du coefficient de clustering local est :
\(c(i) = 2 \times \frac{|e_{xy} \in E | x,y \in N(i) |}{k_i(k_i-1)}\)
la distribution de degrés \(P(k)\). Pour un graphe donné, il s’agit de la fraction de sommets du graphe de degré \(k\). S’il y a \(n\) sommets, et que \(n_k\) d’entre eux ont pour degré \(k\), \(P(k) = \frac{n_k}{n}\). Attention, parfois une confusion est faite avec la distribution cumulative des degrés, désignant la fraction de sommets qui ont un degré au moins égal à \(k\).
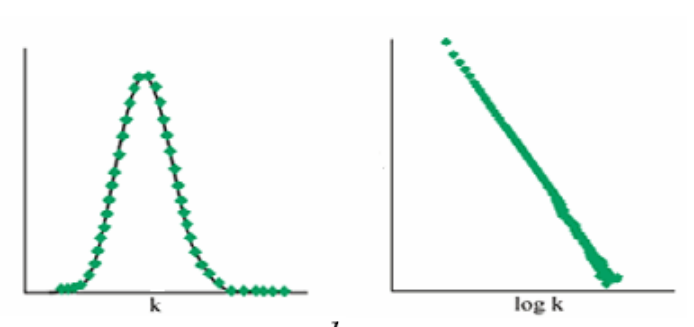
Fig. 92 Distribution (quasi-)gaussienne (à gauche), en loi de puissance à droite¶
les composantes connexes. C’est un ensemble maximal de sommets tel qu’il existe un chemin entre toute paire de sommets dans l’ensemble. Certains graphes sont entièrement connexes. D’autres non, auquel cas il est intéressant de mesurer la taille et le nombre des composantes connexes.
les communautés. Ce sont des ensembles de sommets très liés entre eux et peu liés avec le reste du graphe. Nous étudions en détail dans la seconde partie du cours quelles communautés on peut rechercher dans un graphe et les principales manières de le faire.
la centralité. Pour chaque sommet du graphe, on peut définir plusieurs mesures de centralité, qui estiment à quel point le sommet est « central » dans le graphe :
centralité de degré, égale au degré ;
centralité d’intermédiarité (betweenness centrality) : proportion des plus courts chemins passant par un sommet : \(C(v) = \sum_{s \neq t \neq v \in V} \frac{\sigma_{st}(v)}{\sigma_{st}}\) ;
centralité de proximité : inverse de la distance à tous les autres sommets \(C(v) = \frac{1}{\sum_y d(y,v)}\).
La centralité la plus utilisée est la centralité d’intermédiarité.
Les réseaux réels ont souvent des propriétés assez différentes des graphes aléatoires que l’on peut générer (cf section suivante) :
faible densité,
fort clustering,
faible distance moyenne,
distribution de degrés très hétérogène,
composante connexe géante,
présence de communautés.
Modélisation¶
La modélisation, dans notre contexte, consiste à proposer des modèles de graphes afin de les comparer au graphe étudié et d’estimer si les propriétés observées étaient attendues, ou non. On utilisera souvent des graphes « aléatoires », c’est-à-dire générés par tirage aléatoire en respectant éventuellement une loi (contraignant la distribution de degrés, la densité, etc.).
On peut, dans un premier temps, utiliser un modèle uniforme, en se donnant \(n\) sommets et en décidant que chaque arête a une probabilité \(0<p<1\) d’exister (modèle de Gilbert, noté \(G(n,p)\)). On observe alors en général une composante connexe géante, un diamètre proche de \(log(n)\), un clustering très faible, une distribution de degrés homogène, pas de structure communautaire (cf liste précédente sur les réseaux réels).
Il existe de nombreux autres modèles pour générer des graphes et permettre d’affiner l’analyse.
Le modèle de l’attachement préférentiel, qui permet de générer des réseaux « sans échelle » (scale-free) a été proposé par Barabási et Albert [AB02]. On débute la création du graphe aléatoire avec \(m_0\) sommets, puis on ajoute successivement chacun des nœuds. Ceux-ci sont connectés à \(m\) sommets, avec une probabilité qui dépend du degré de chacun des nœuds. Formellement, la probabilité \(p_i\) que le nouveau nœud soit connecté au nœud \(i\) est \(p_i = \frac{k_i}{\sum_j k_j}\). Cette règle de génération fait que les nœuds qui ont déjà des connexions ont tendance à en recevoir toujours davantage, ce qui crée des « hubs », et une distribution de degrés qui est asymptotiquement une « loi de puissance ».
Le modèle configurationnel permet d’obtenir une distribution de degrés fixée : on prend \(n\) sommets, on fixe le degré de chaque sommet, on ajoute des liens au hasard en respectant les degrés.
Parmi ces modèles, celui de l’attachement préférentiel donne un clustering significativement supérieur (les autres étant très faibles).
Quelques applications de la modélisation¶
La modélisation, et les simulations qu’elle autorise, permettent d’étudier de nombreux phénomènes reposant sur des graphes, et de comprendre ce qui se passe dans des réseaux réels.
Citons en particulier :
les phénomènes de diffusion épidémique, que ce soit pour des virus informatiques ou pour des agents infectieux d’êtres vivants. Voir les modèles SI / SIR pour plus de détails ;
les phénomènes d’atteintes aux réseaux, que ce soit des pannes aléatoires ou des attaques ciblées.
On examine en particulier pourquoi et où peuvent se produire des ruptures de connexité dans le graphe.
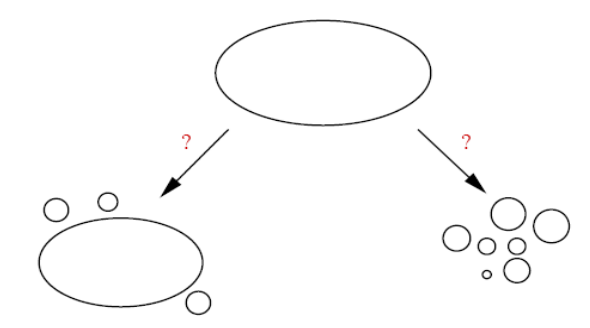
Fig. 93 Ruptures de connexité liées à une atteinte au système. Il peut résulter un certaine stabilité (grande composante connexe, peu d’îlôts créés, à gauche) ou un morcellement du réseau (à droite)¶
Algorithmique¶
La représentation informatique des graphes peut se faire sous différentes formes. On peut utiliser des listes d’adjacence, c’est-à-dire des listes chaînées ou des tableaux de longueurs variables, ce qui présente l’intérêt d’accéder avec un coût faible aux successeurs d’un nœud dans un graphe orienté (mais rend plus complexe la recherche de ses prédécesseurs).
Une représentation privilégiée reste bien sûr la matrice d’adjacence \(A\), dont les coefficients binaires valent 0 quand il n’y a pas d’arête entre le nœud \(i\) et le nœud \(j\), 1 si oui.
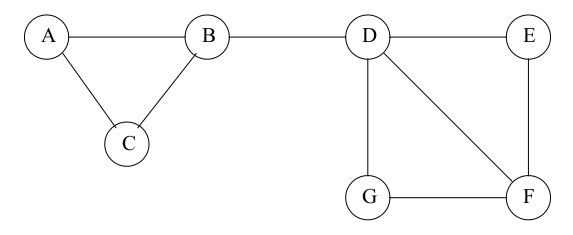

Attention cependant, la taille de la matrice est de l’ordre de \(n^2\), ce qui peut la rendre énorme pour des graphes de taille importante. Elle est néanmoins souvent creuse (de nombreux zéros, car de nombreux nœuds ne sont pas interconnectés) et les frameworks récents disposent d’optimisations intéressantes pour stocker et traiter de telles matrices (mais cela peut ne pas être suffisant).

On définit également la matrice des degrés \(D\), diagonale, comportant le degré du nœud \(i\) sur la \(i\)-ème ligne. Enfin, on évoquera dans le prochain cours l’utilisation de la matrice laplacienne, définie comme \(L = D - A\).
Difficultés algorithmiques¶
Les graphes et réseaux sociaux étudiés sont régulièrement de grande taille et posent des difficultés, il n’est pas toujours possible de stocker l’entièreté du graphe ou d’effectuer dessus des calculs qui aboutissent en un temps raisonnable. Si on note par \(n\) le nombre de sommets et par \(m\) le nombre d’arêtes, compter les triangles du graphes, par exemple, se fait naïvement avec une complexité \(O(n^3)\), mais des algorithmes efficaces ont été construits pour pouvoir le faire avec une complexité \(O(m \times n^{1/a})\) dans les cas où la distribution de degrés est en loi de puissance d’exposant \(a\). De même, calculer le diamètre d’un graphe a une complexité théorique de \(O(nm)\), mais on peut avoir une bonne estimation en \(O(m)\). Beaucoup de problèmes (et de calculs) sont NP-complets et nécessitent des heuristiques appropriées.
Deux algorithmes classiques¶
Pour parcourir un graphe, on dispose de deux possibilités, le parcours en largeur et le parcours en profondeur. On les utilise souvent au sein d’autres algorithmes. On les illustre ici sur le graphe suivant :
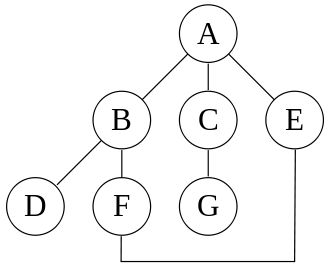
Fig. 94 Graphe pour présenter les parcours en profondeur et en largeur¶
Pour le parcours en profondeur (DFS, ou Depth-First Search):
à partir d’un sommet S, appelé racine, on appelle récursivement cet algorithme pour tous les voisins de S ;
pour chaque sommet \(i\), on le marque puis on prend le premier sommet voisin et on explore tous les sommets (non marqués) avant de revenir à \(i\) ;
sur notre graphe, avec S = A, l’ordre de visite est donc : A, B, D, F, E, C, G ;
l’implémentation de l’algorithme repose sur une pile.
Pour le parcours en largeur (BFS, ou Breadth-First Search) :
pour chaque sommet, on le marque, puis on repère tous ses voisins et on stocke tous ceux qui ne sont pas marqués dans une file ; on continue avec le sommet suivant dans la file ;
sur notre graphe, en partant de A, l’ordre de visite est donc : A, B, C, E, D, F, G ;
cet algorithme permet de calculer des distances entre nœuds (cf deuxième partie).
Logiciels et outils¶
Avec l’explosion de la taille moyenne des graphes étudiés et les avancées significatives dans leur traitement, de nombreux frameworks et bibliothèques dédiés sont apparus aux cours des dix dernières années.
Le projet GraphLab, né à Carnegie Mellon University en 2009, repose sur des routines en C++ et dispose de très bonnes performances. Le calcul est distribué et il est disponible sous licence Apache (open source). Nous avons utilisé en travaux pratiques GraphX, qui en est l’implémentation Spark. Actuellement nous employons plutôt GraphFrames, qui propose des API en Java, Scala et Python.
Google, dont le cœur de métier repose sur le calcul du PageRank sur le graphe du Web, a développé de son côté Pregel [MABDHLC10]. Les calculs reposent sur des passages de messages entre nœuds. Plusieurs implémentations existent au-dessus d’Hadoop.
D’autres frameworks plus ou moins stables existent, Giraph, FlockDB, AllegroGraph, etc. Une base de données « orientée graphes » a beaucoup de succès en ce moment, Neo4j ; elle est open source.
Quelques logiciels dédiés sont également disponibles, dont Gephi, commencé comme projet étudiant à l’Université Technologique de Compiègne et open source. Il permet l’analyse de graphes de tailles raisonnables, intègre de nombreux algorithmes et traitements classiques (PageRank, modularité, plus courts chemins, etc.), le tout en permettant un ajustement fin de la visualisation finale.
Références¶
Ce cours repose sur les travaux de l’équipe ComplexNetworks du LIP6 au sein duquel l’auteur a effectué son travail de doctorat. En particulier, les cours de Jean-Loup Guillaume ont été une source d’inspiration précieuse, de même que le livre Mining massive datasets [MMDS] et le matériel associé.
Albert, R. and Barabási, A.-L. Statistical mechanics of complex networks. Reviews of Modern Physics. 2002. 74: 47–97.
Granovetter, M. S. The Strength of Weak Ties. American Journal of Sociology, Volume 78, Issue 6 (May, 1973), 1360–1380.
Kleinberg, J. M. Navigation in a small world. Nature. 2000 Aug 24;406(6798):845. http://www.nature.com/nature/journal/v406/n6798/full/406845a0.html#B2
Travers, J. and Milgram, S. An experimental study of the small world problem. Sociometry, Vol. 32, No. 4. (Dec., 1969), pp. 425-443. http://www.jstor.org/stable/2786545
Grzegorz Malewicz, Matthew H. Austern, Aart J. C. Bik, James C. Dehnert, Ilan Horn, Naty Leiser, and Grzegorz Czajkowski. Pregel: A System for Large-Scale Graph Processing. SIGMOD 2010. https://kowshik.github.io/JPregel/pregel_paper.pdf
Leskovec, J., Rajaraman, A. and J. D. Ullman. Mining of Massive Datasets. Cambridge University Press, New York, NY, USA, 2011. Accessible en version numérique http://www.mmds.org
Watts, D. J. and Strogatz, S. H. Collective dynamics of “small-world” networks. Nature 393, 440-442. http://www.nature.com/nature/journal/v393/n6684/full/393440a0.html


