Cours - Détection de communautés dans les graphes¶
Supports complémentaires :
Vous pouvez télécharger les diapositives du cours (1 par page) qui sont projetées durant la séance.
Nous nous intéressons dans ce chapitre à la recherche de communautés dans des graphes. Par communauté on entend ici sous-ensemble de nœuds qui sont fortement interconnectés, c’est-à-dire qu’il existe entre eux un nombre important de connexions, davantage que ce que ces nœuds entretiennent avec les autres membres du réseau. Contrairement à des réseaux générés aléatoirement, les réseaux sociaux (et d’autres graphes) présentent une propriété de localité : les nœuds tendent à s’interconnecter en groupes, plus ou moins denses. Cela peut résulter de phénomènes liées aux structures humaines (des élèves regroupés dans une classe, des sportifs dans une équipe), ou de la transitivité (on présente nos amis les uns aux autres, certains vont ensuite devenir amis, alors qu’il n’y aurait pas eu de lien entre eux sans nous).
Les motivations de l’analyse des communautés sont similaires à celle de l’analyse des graphes en général. Comme on l’a vu au chapitre précédent, on cherche à comprendre comment fonctionne le système que l’on a modélisé par un graphe. Quels sont les échanges (d’information, d’argent, etc.) entre les membres ? Pourquoi M. X et Mme Y ont des chances de devenir amis, mais peu de rencontrer un jour Mme Z ? On peut également se servir des communautés pour élaborer des systèmes de recommandations. Mme AA, M. BB et Mme CC ont l’air d’avoir des centres d’intérêts en commun, si je recommande à Mme CC les films qu’apprécient AA et BB, ça devrait aussi lui plaire.
Il existe différents types de communautés. On peut dans un premier temps rechercher un partitionnement du graphe (c’est-à-dire où chaque nœud appartient à une et une seule communauté). On peut alors utiliser des techniques de clustering classiques, ou des algorithmes dédiés aux graphes, comme on le verra dans ce chapitre. Mais, dans un réseau social, les communautés sont souvent recouvrantes : un individu est relié à divers groupes d’amis ou de collègues dont les membres se connaissent peu. La Fig. 96 présente un réseau partitionné, avec des communautés non recouvrantes, alors que la Fig. 97 montre les communautés auxquelles appartient une personne (appelée « ego u »). Voir aussi les Réseaux de connaissances professionnelles du premier chapitre.
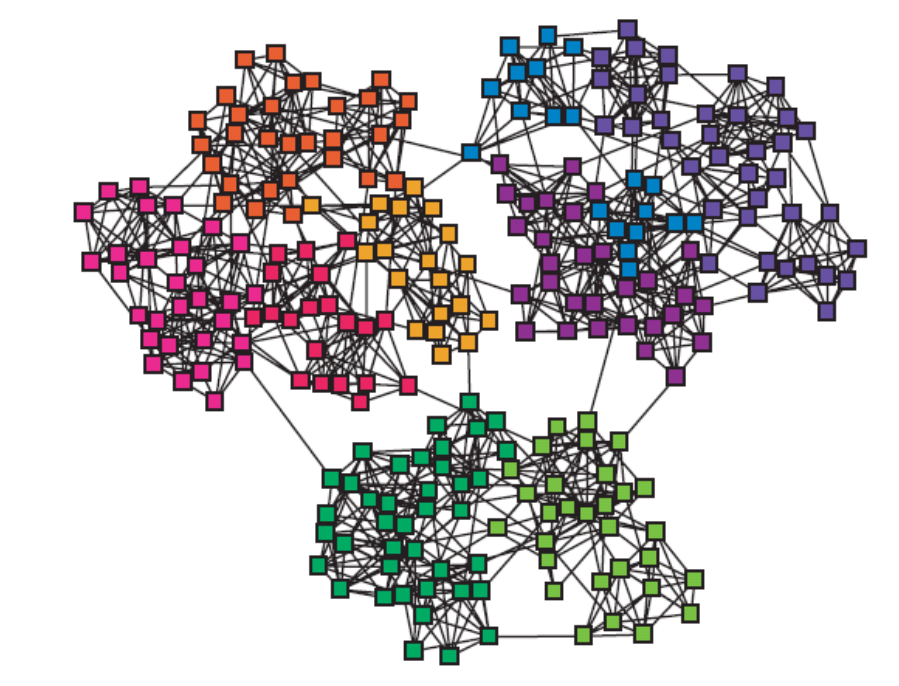
Fig. 96 Modules¶
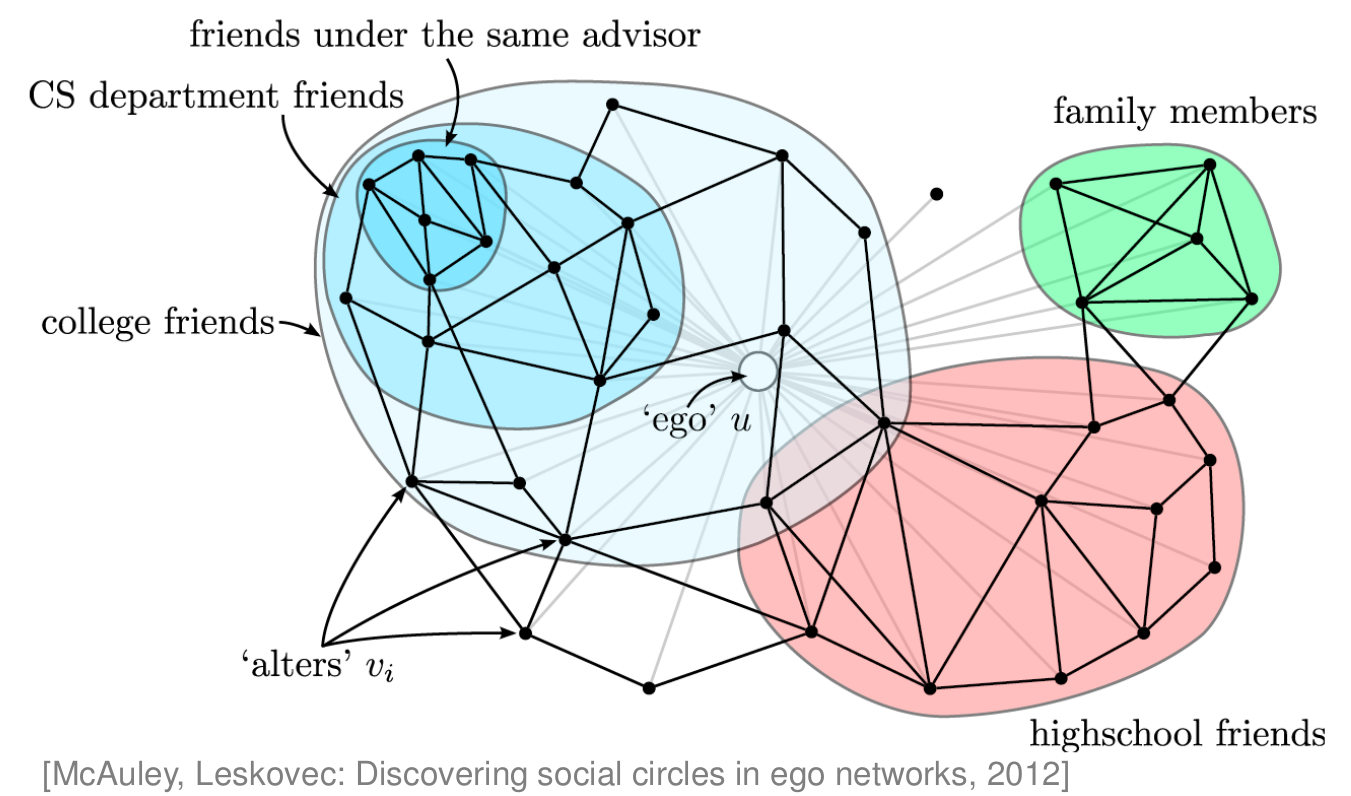
Fig. 97 Réseau social égocentré¶
Note
Nous n’aborderons pas dans ce chapitre l’aspect important mais délicat (car toujours sujet à de nombreuses recherches) du suivi temporel des communautés. Après avoir repéré des communautés sur un graphe à un instant t, il est souvent difficile de savoir (algorithmiquement) si les communautés détectées à t+1 sont le résultat de fusion/scission de communautés précédentes. Nous nous contentons donc ici d’oberserver des graphes « figés ».
Des sous-graphes intéressants¶
La théorie des graphes a mis en évidence de nombreuses manières de définir des sous-graphes présentant une cohésion forte, c’est-à-dire des sous-ensemble de nœuds ou d’arêtes particuliers :
une composante k-connexe est un ensemble de sommets tels qu’il existe au moins \(k\) chemins disjoints entre chaque paire de sommets. On parle simplement de composante connexe quand \(k=1\).
une clique est un sous-graphe complètement connecté : chaque sommet est connecté à tous les autres.
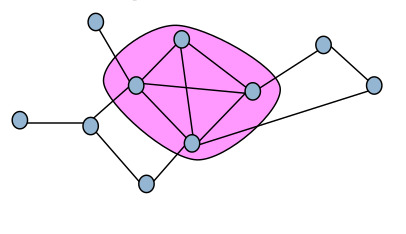
une n-clique est un sous-graphe \(G'\) tel que la distance entre les nœuds de \(G'\) soit inférieure à \(n\) dans \(G\). L’ensemble \(G'\) peut ne pas être connecté ou avoir un diamètre supérieur à \(n\).
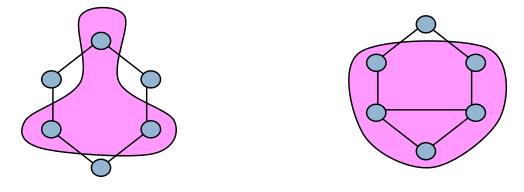
un n-clan est une n-clique de diamètre \(n\) au plus.
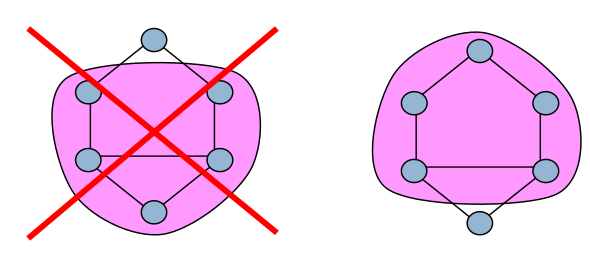
Un n-club est un sous-graphe de diamètre maximal \(n\).
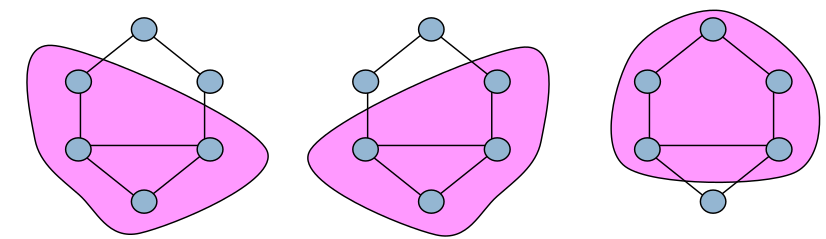
On peut lister encore de nombreux autres sous-graphes cohésifs :
k-degree set : sous-graphe dans lequel tous les sommets ont un degré d’au moins k.
k-plex : sous-graphe maximal H tel que chaque sommet est connecté à au moins \(|H|-k\) sommets.
LS set : sous-graphe tel que ses sommets sont plus connectés aux autres sommets du sous-graphe qu’avec l’extérieur.
alpha set : sous-graphe tel que chaque sommet a plus de liens internes que sortants.
La recherche de ces zones sur un graphe donné est en général un problème coûteux. Dans de nombreux cas, il s’agit de problèmes NP-complet (cliques, k-plex). Parfois, c’est polynomial (LS set). Cela rend bien sûr le passage à l’échelle très délicat. Il en est de même pour la recherche de communautés recouvrantes, souvent coûteuse. Nous allons donc voir d’autres techniques pour trouver des « communautés » (ou groupes, clusters, modules).
Clustering hiérarchique¶
Il existe une manière ascendante et une manière descendante de procéder au regroupement hiérarchique (ou clustering hiérarchique).
Approche ascendante¶
Voici un algorithme générique pour une classification ascendante :
Au départ, chaque sommet est une communauté.
Calculer la distance entre chaque paire de communautés.
Fusionner les deux plus proches.
Revenir à 2.
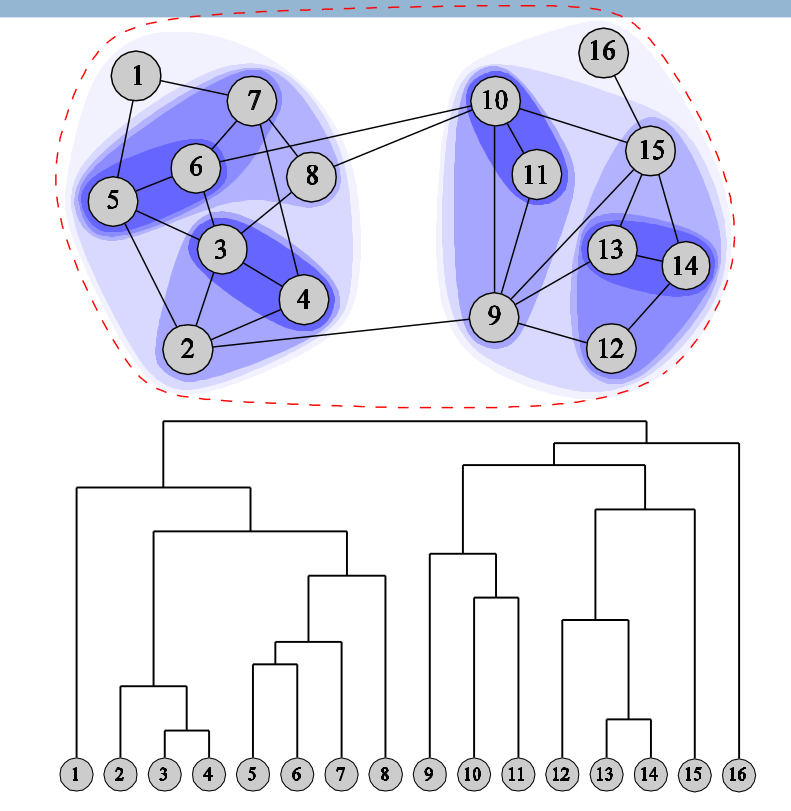
Fig. 98 Clustering hiérarchique ascendant¶
On obtient un dendrogramme et un découpage du graphe en communautés, comme le présente la Fig. 98. Différentes mesures de distance entre les communautés peuvent être choisies, par exemple le minimum, le maximum ou la moyenne des distances entre paires de nœuds (que l’on calcule généralement avant).
Approche divisive¶
Il existe aussi une approche divisive, proposée par Girvan et Newman en 2002, qui est assez efficace. Elle repose sur l’idée suivante : si un lien se trouve fréquemment sur les plus courts chemins entre les nœuds du graphe, alors il est naturel de penser qu’il ne se trouve pas « au sein d’une communauté donnée », mais plutôt qu’il relie des portions distantes du graphe, des communautés distinctes. En retirant itérativement le lien qui a la plus forte « centralité », on obtient un découpage en blocs de notre réseau.
À titre d’analogie, on peut penser au réseau de transport français : la liaison de TGV Paris-Lyon se trouve sur les plus courts chemins entre de nombreuses villes, par exemple Rennes-Marseille, Rennes-Lyon, Rouen-Lyon, Lille-Valence. En revanche, la liaison Rouen-Rennes n’est un plus court chemin qu’entre les villes normandes et bretonnes. Si l’on retire la liaison Paris-Lyon (et quelques autres liaisons Nord-Sud importantes), on va obtenir un partitionnement Nord-Sud du réseau.
Voici le détail de l’algorithme :
on calcule la centralité (betweenness) de chaque lien (c’est une extension de la notion de centralité pour les nœuds vue dans le chapitre précédent) ;
on enlève le lien de plus forte centralité ;
on recommence jusqu’à ce qu’il n’y ait plus de lien ;
on obtient une décomposition hiérarchique du réseau.
La Fig. 100 présente les différentes étapes de l’algorithme, appliquées au graphe de la Fig. 99. La Fig. 101 montre le résultat du clustering sur le graphe du Karaté-club étudié par Zachary.
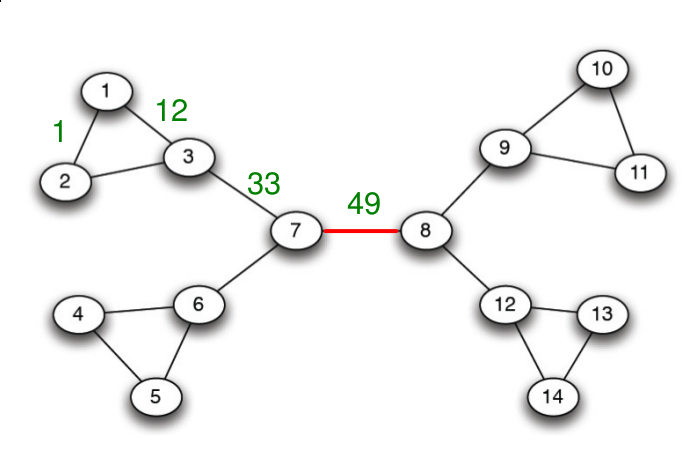
Fig. 99 Graphe pour la présentation de l’algorithme de Girvan-Newman¶
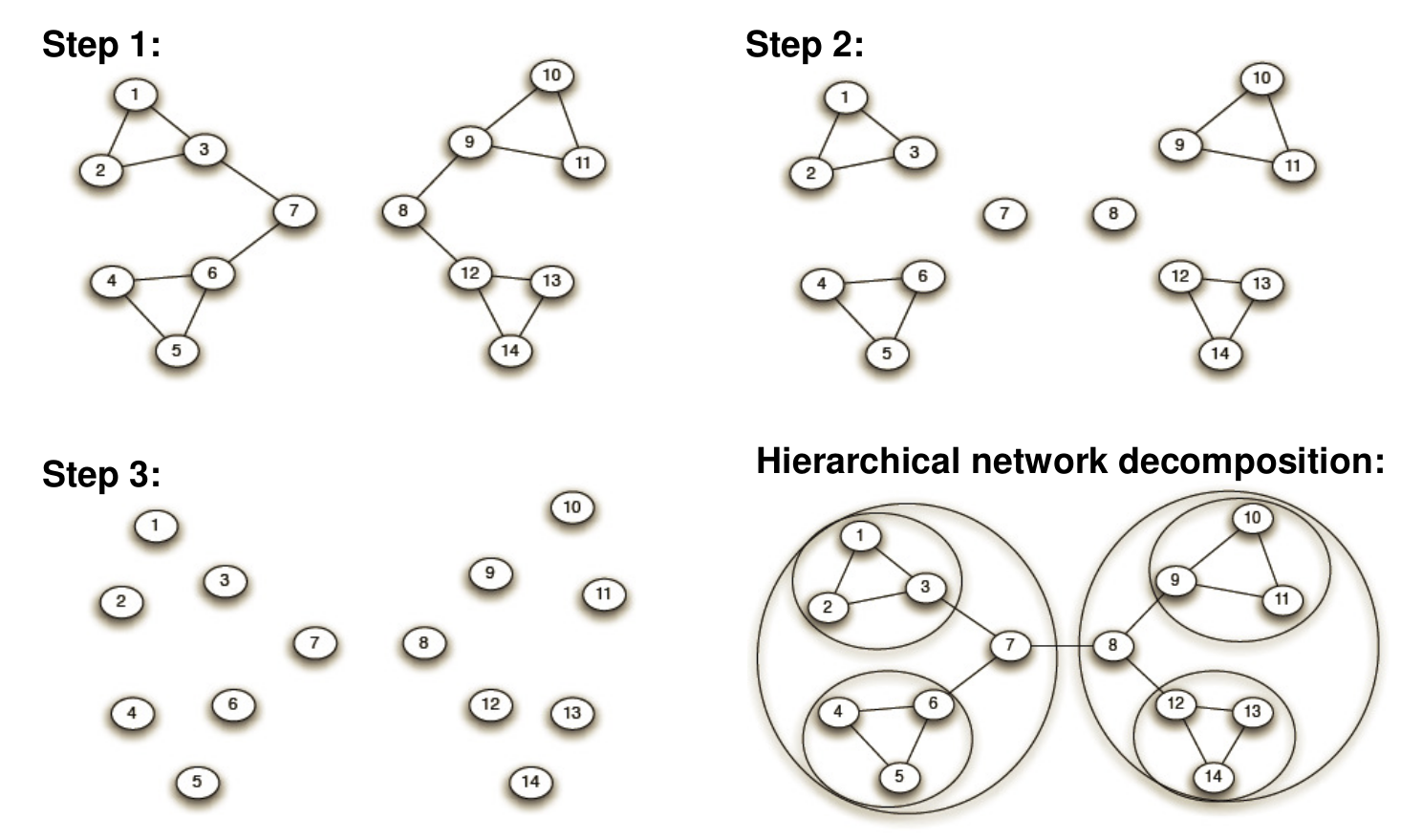
Fig. 100 Étapes de l’algorithme de Girvan-Newman¶
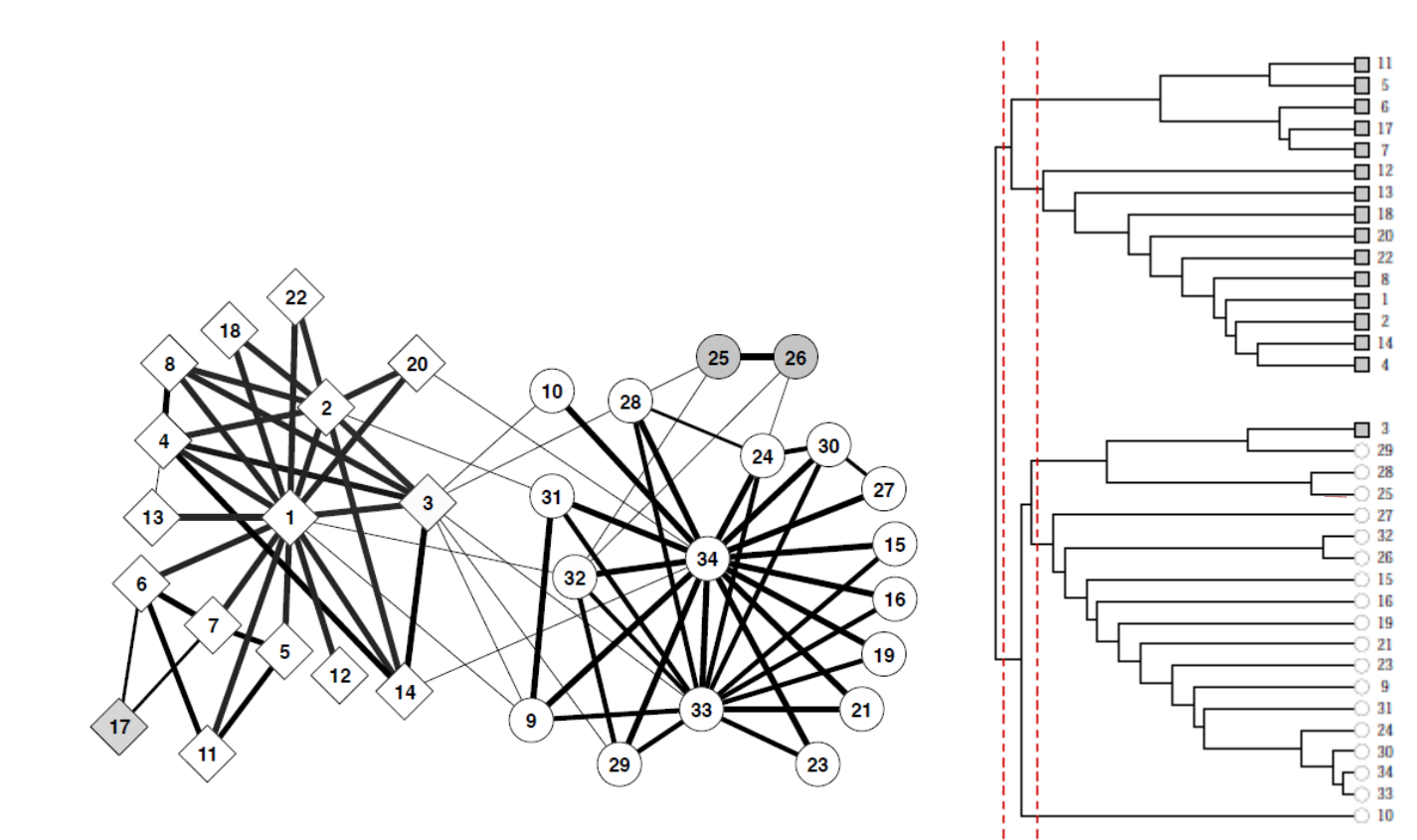
Fig. 101 Application de l’algorithme de Girvan-Newman au graphe du Karaté Club de Zachary¶
Calcul de la centralité¶
L’algorithme de Girvan-Newman repose sur un calcul de centralité, présenté dans les diapos du cours. Vous pouvez également consulter le livre Mining Massive Datasets [MMDS], pages 333 et suivantes.
Évaluer la structure communautaire : la modularité¶
On a défini une communauté comme un sous-graphe dont les sommets sont plus liés entre eux qu’avec le reste du réseau. C’est une notion pour l’instant non formalisée mathématiquement. Il peut donc être intéressant de se donner une métrique pour évaluer la qualité du partitionnement d’un graphe en communautés.
La modularité, également introduite par Newman, permet de caractériser cela. Elle est définie comme la différence normalisée entre le nombre de liens présents dans un module (ou groupe, ou cluster, ou communauté) et le nombre de liens attendus dans un graphe aléatoire. La valeur de la modularité est dans l’intervalle [-1;1]. On calcule une valeur de modularité pour un partitionnement donné du graphe, on note traditionnellement la valeur de la modularité par la lettre Q.
Détaillons un peu le calcul. On dispose d’un partitionnement de notre graphe en communautés, de notation générique s. On note par S l’ensemble des communautés. On souhaite que
où \(\propto\) indique la proportionnalité. La fraction du nombre de liens du graphes qui sont « internes » aux communautés dans le graphe est obtenue par la formule :
où \(m\) est le nombre total de liens dans le graphe et \(A_{ij} = 1\) si le lien ij existe, 0 sinon.
Il nous faut donc un modèle aléatoire auquel comparer le partitionnement considéré. On se réfère pour cela au modèle configurationnel, qui est une manière de générer un graphe aléatoire à partir d’un graphe existant. Ce modèle conserve les degrés des sommets du graphe. On fait de chaque lien un « demi lien » partant de chaque nœud et on « recâble » les demi-liens du graphe aléatoirement. La probabilité d’avoir un lien entre les nœuds v et w est alors \(\frac{k_v k_w}{2m}\), si \(k_v\) et \(k_w\) sont les degrés de v et w.
En insérant ce terme dans la formule précédente, on obtient la valeur de la modularité :
La modularité est positive si le nombre de nœuds dans les modules est supérieur à ce que l’on pourrait attendre avec un graphe aléatoire. Elle tend vers 0 si l’on prend un partitionnement aléatoire d’un graphe aléatoire. Au-dessus d’une valeur de 0.3 environ, on peut considérer que l’on a une structure communautaire significative.
En utilisant la valeur de la modularité pour différents partitionnements, on peut décider quel partitionnement est souhaitable pour un graphe donné, comme le montre la Fig. 102. On a un graphe partitionné en 4 grandes communautés, elles aussi subdivisées. Mais l’on constate que le meilleur partitionnement, au sens de la modularité, est obtenu lorsque l’on s’arrête à cette division du graphe en 4 groupes.
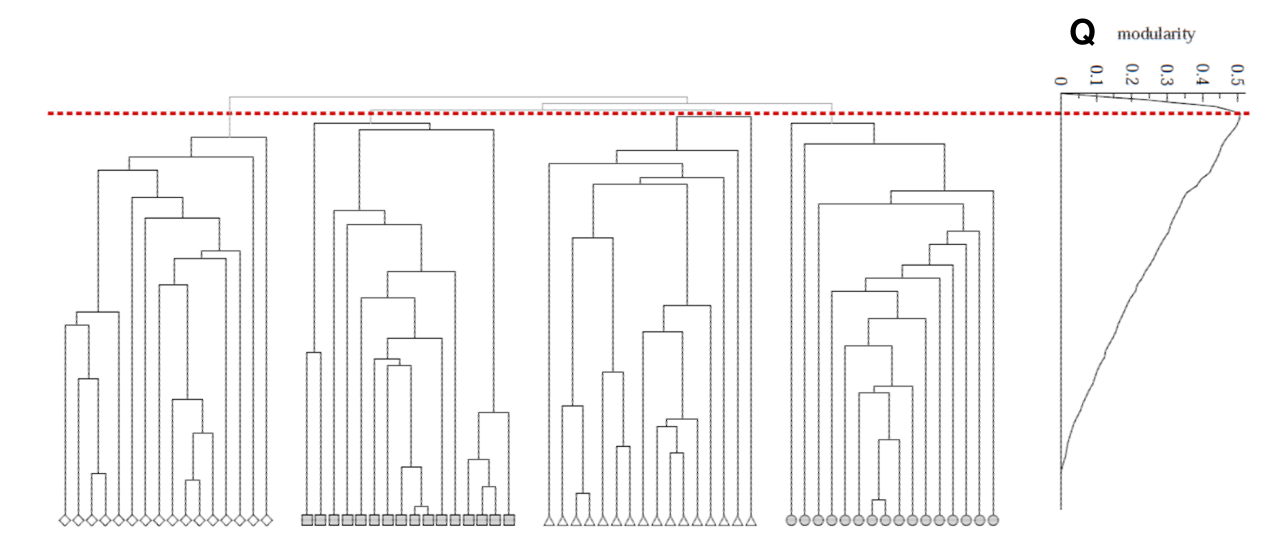
Fig. 102 Sélection d’un partitionnement avec la modularité¶
La complexité de l’algorithme de Girvan-Newman est \(O(m^2n)\). Nous verrons dans la section suivante une manière différente et de complexité plus faible pour optimiser la modularité.
Optimiser la modularité : l’algorithme de Louvain¶
En 2008, des chercheurs français et belges de l’Université de Louvain ont proposé un nouvel algorithme cherchant à maximiser, à chaque étape, la modularité [BGLL08].
L’algorithme repose sur deux phases distinctes, qui sont répétées itérativement. Au départ, tous les nœuds du graphe sont indépendants : il y a autant de communautés que de nœuds dans le graphe.
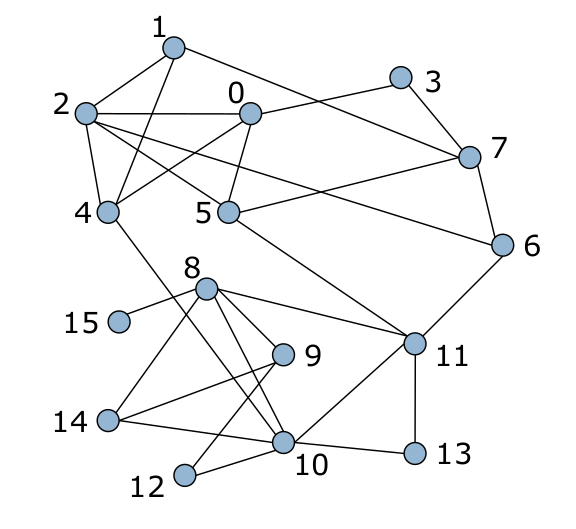
Ensuite, pour chaque nœud \(i\) du graphe on considère chacun de ses voisins \(j\) et l’on évalue le gain de modularité que l’on obtiendrait en retirant \(i\) de sa communauté pour le mettre dans celle de \(j\).
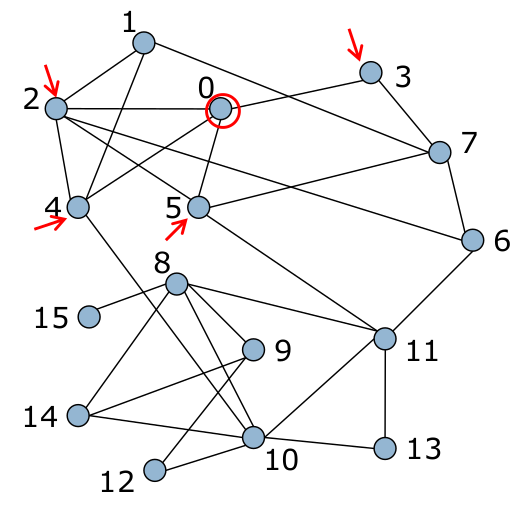
Fig. 103 État initial¶
Le nœud \(i\) est ensuite placé dans la communauté pour laquelle le gain de modularité est maximal, à condition que ce gain soit positif (sinon, \(i\) reste dans sa communauté).
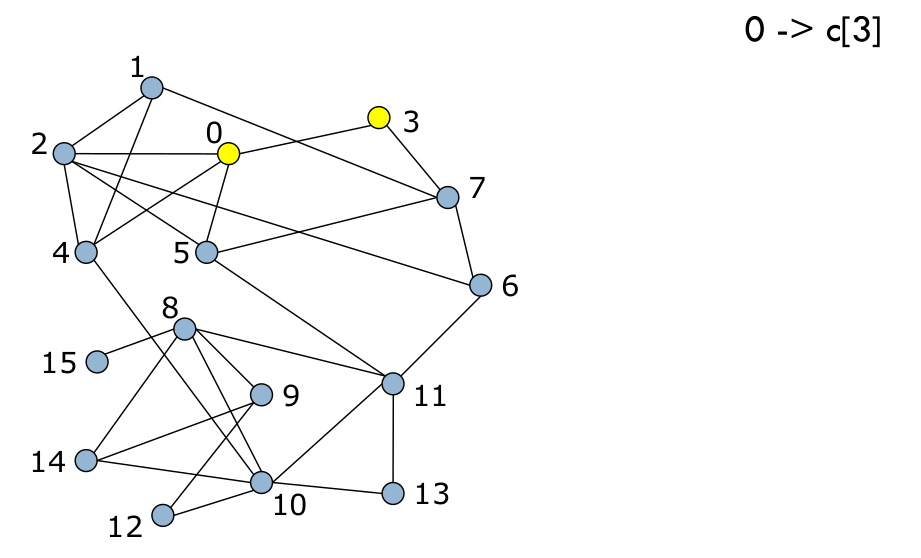
Ce processus est appliqué au nœud suivant (Fig. 104 et Fig. 105), et ainsi de suite pour tous les nœuds (Fig. 106).
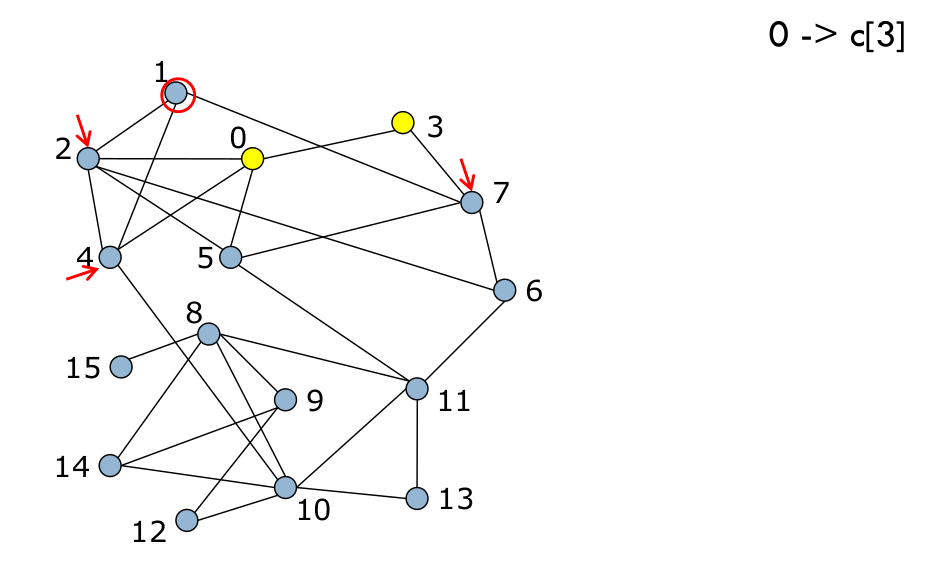
Fig. 104 suite¶
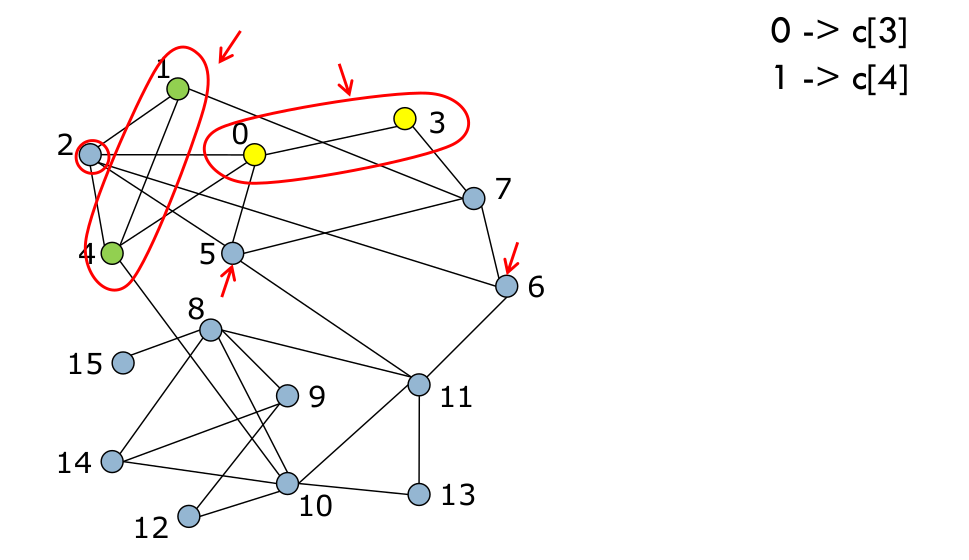
Fig. 105 2¶
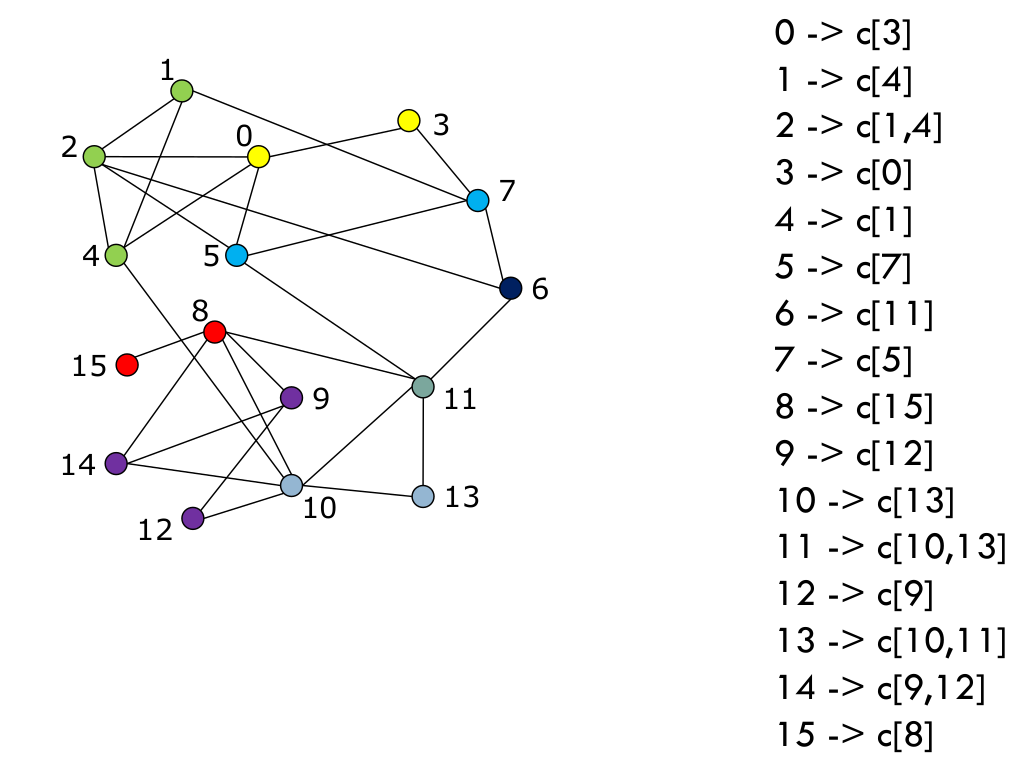
Fig. 106 On répète pour tous les nœuds¶
Cette séquence est ensuite répétée (Fig. 107), jusqu’à ce qu’il n’y ait plus d’amélioration. C’est la fin de la première phase, on a atteint un maximum local de la modularité.
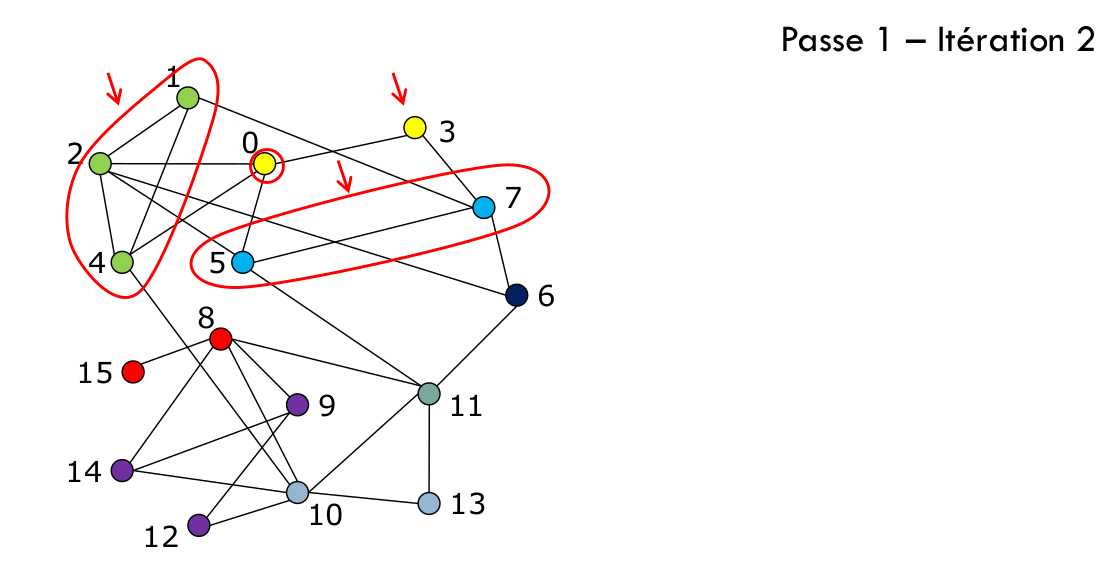
Fig. 107 On itère, en réessayant d’optimiser localement la modularité avec les communautés formées à l’itération précédente¶
La deuxième phase de l’algorithme consiste à construire un nouveau graphe dont les nœuds sont les communautés trouvées dans la première phase. Les liens entre ces « super-nœuds » sont « valués », avec un poids correspondant au nombre de liens entre les nœuds de chacune des communautés qu’ils représentent. Les liens internes de chaque communauté forment des boucles (voir Fig. 108, flèche rouge).
Une fois que cette deuxième phase est terminée, cela clôt une « passe » de l’algorithme. Ensuite à la lieu la passe suivante, qui commence donc par la première phase : une détection communautaire sur le nouveau graphe (celui en haut à droite dans la Fig. 108). On trouve des communautés (fin de phase 1), qui sont ensuite transformées en nœuds (fin de phase 2). Les passes sont répétées, jusqu’à atteindre un maximum de modularité.
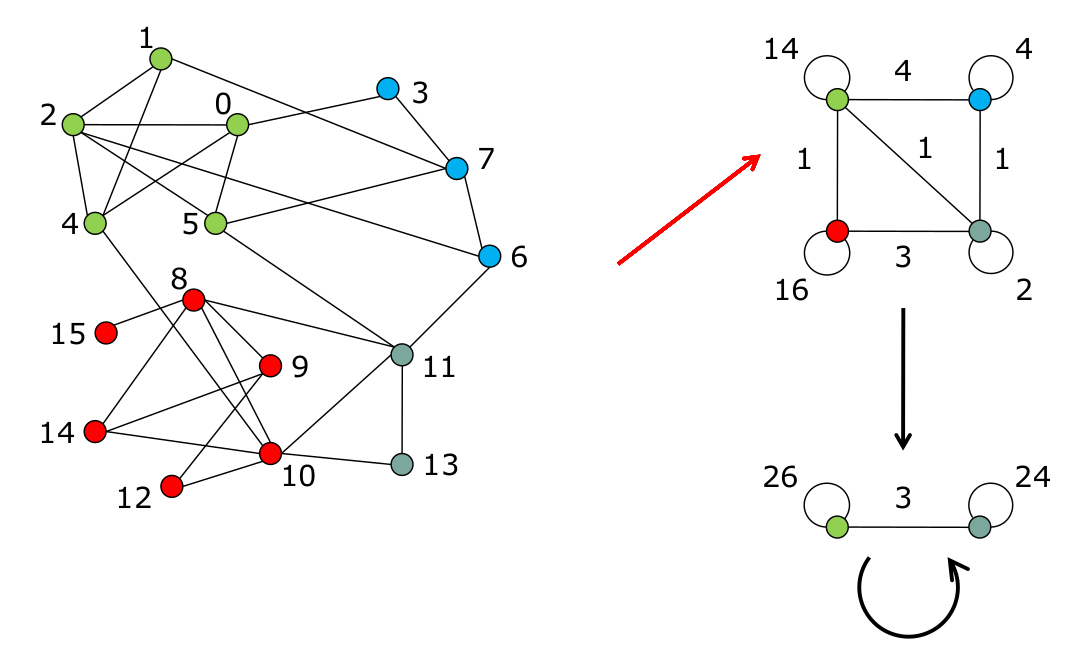
Fig. 108 Deuxième Phase¶
Par construction, le nombre de communautés diminue donc à chaque passe, la première passe est donc la plus gourmande en temps de calcul. On obtient une décomposition hiérarchique des communautés du graphe. Au niveau supérieur, de très « grosses » communautés regroupant des communautés des niveaux inférieurs. Le nombre total de niveaux dans la hiérarchie est déterminé par le nombre de passes, qui est généralement faible (moins de 10).
L’algorithme est simple et d’implémentation facile. Son avantage principal, bien sûr, reste son efficacité : comme il nécessite le stockage en mémoire de peu d’informations et que l’essentiel du calcul se fait dans les premières passes, il permet de traiter sur des machines traditionnelles des graphes qui auparavant devaient être traitées sur des serveurs bien plus puissants. Il est possible d’améliorer l’algorithme en remarquant que les dernières passes apportent un gain de modularité faible, on peut donc décider de s’arrêter quand le gain entre une passe et la suivante est inférieur à un certain seuil.
Deux aspects importants à noter. Au début de la première phase, les nœuds sont numérotés aléatoirement, et c’est sur cet ordre que repose le test qui consiste à « prendre chaque nœud et tester son déplacement dans une communauté voisine ». Ainsi, si l’on exécute deux fois l’algorithme sur les mêmes données, le résultat pourra être sensiblement différent. On dit que l’algorithme n’est pas déterministe.
D’autre part, il existe un phénomène dit de « limite de résolution » de la modularité, que l’on peut observer sur un exemple. Si l’on considère un graphe formé d’un « anneau de cliques », comme dans la Fig. 109, on s’attend à ce que la partition de meilleure modularité soit celle où chaque communauté est une clique.
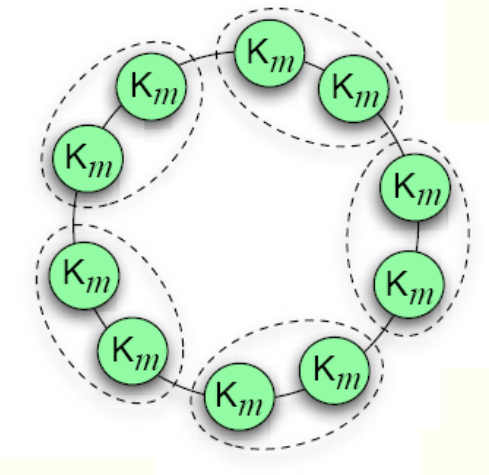
Fig. 109 Anneau de cliques : un cercle vert est une clique de \(m\) sommets. Une arête relie un des \(m\) sommets de la clique à un autre sommet de la clique voisine.¶
Pourtant, effectuons le calcul. Il y a \(n\) cliques de taille \(m\), donc la modularité de la partition en « cliques » donne :
La modularité de la partition en paires de cliques est :
Ainsi, \(Q_{single} > Q_{pairs} \iff m (m-1)+2 > n\), de sorte que, pour \(m = 5\) et \(n = 30\), on obtient une modularité plus élevée pour la partition qui regroupe les cliques deux à deux (\(Q=0.888\)) que pour la partition où chaque clique est seule dans sa communauté (\(Q=0.876\)). Cela permet de caractériser cette « limite de résolution de la modularité » : dans un même graphe avec des communautés de tailles différentes, il est possible que certaines d’entre elles ne soient pas détectées. C’est un problème qui est lié à l’emploi de la modularité comme métrique et non à l’algorithme de Louvain lui-même.
Un exemple d’utilisation de l’algorithme de Louvain en Python est disponible dans ce script Python. Le logiciel Gephi incorpore aussi cet algorithme.
Autres approches¶
Partitionner un graphe peut aussi se faire avec d’autres approches. Une technique classique consiste à tenter de minimiser ce qu’on appelle le cut, c’est-à-dire le nombre de connexions intergroupes coupées par notre partitionnement. On peut définir le cut entre deux ensembles \(A\) et \(B\) de sommets comme « le nombre de liens qui ont exactement un sommet dans chacun des groupes ». On le note \(cut(A,B)\).
Voyons sur un exemple, Fig. 110. Si l’on découpe ce graphe en deux sous-ensembles A et B, le cut est de 2.
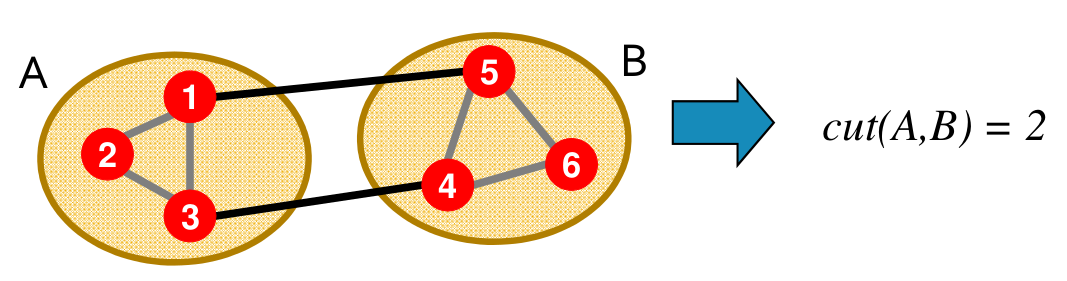
Fig. 110 Calcul du cut¶
Comme on peut le voir avec la Fig. 111, minimiser le cut peut cependant poser des problèmes : le minimum est atteint en coupant en deux groupes qui sont de tailles très déséquilibrées, un groupe ne contenant qu’un seul sommet.
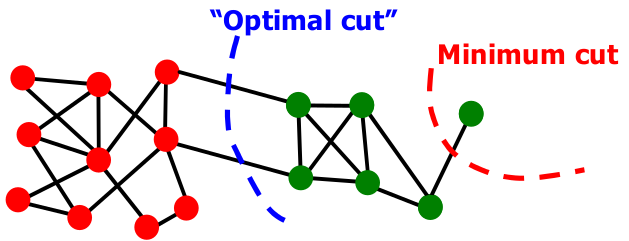
Fig. 111 Prendre le « minimum cut » seul conduit à favoriser des communautés de tailles déséquilibrées¶
On utilise donc généralement une mesure normalisée, le normalized cut. Si l’on définit le nombre de liens qui ont une extrémité dans A comme le volume de A (noté \(vol(A)\)), le normalized cut entre deux groupes vaut :
On obtient des partitions de taille plus équilibrées. Une démonstration mathématique un peu longue pour figurer ici (mais tout à fait accessible via l’article [SM00], ou [MMDS] pages 344 et suivantes) montre que l’on peut trouver cette valeur minimale de normalized cut en recherchant la deuxième valeur propre la plus faible de la matrice laplacienne du graphe (la plus faible étant toujours 0) et le vecteur propre associé.
Éléments pour des systèmes de recommandation « orientés graphes »¶
L’analyse de graphes et réseaux sociaux peut aussi être mise à profit pour élaborer des systèmes de recommandation. Ceux-ci visent à filtrer la quantité d’information aujourd’hui disponible dans certains systèmes (catalogue des produits d’un vendeur en ligne, publications scientifiques dans une discipline, films à voir en VOD, etc.). Les techniques classiques reposent sur une analyse de la matrice encodant les informations de l’historique du système : quel utilisateur a vu/aimé/acheté quoi ? Un calcul de similarité entre utilisateurs ou entre articles permet ensuite de proposer des éléments pertinents (films à voir, produits à acheter), qui auraient été perdus dans la masse des résultats avec un moteur de recherche classique.
On peut utiliser une représentation sous forme de graphe biparti pour visualiser les interactions ayant eu lieu dans le système, comme le montre la Fig. 112. Les utilisateurs sont reliés aux éléments qu’ils ont déjà vus (ou appréciés), avec un poids généralement proportionnel à l’intensité de cette interaction.
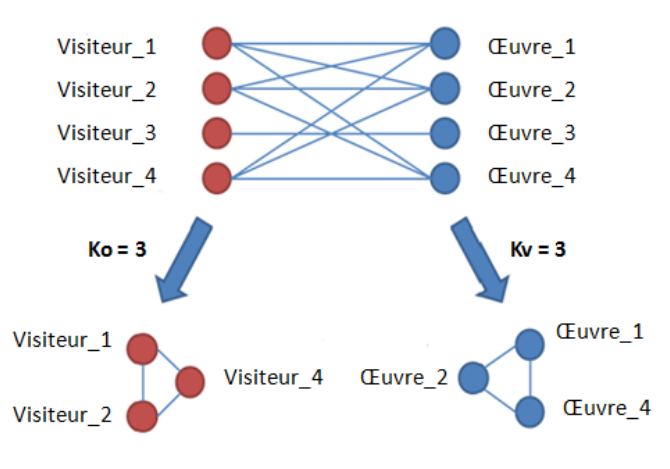
Fig. 112 Graphe biparti d’un système dans lequel interagissent des utilisateurs et des éléments (ici, des visiteurs et des œuvres dans un musée)¶
S’il existe des techniques spécifiques de calcul de communautés sur des graphes bipartis, il est souvent préférable de procéder à une opération dite de projection du graphe biparti. Celle-ci consiste à se ramener à un graphe ne comportant qu’un seul des deux ensembles de nœuds du graphe initial (des utilisateurs ou des articles, donc). Pour cela, on conserve tous les sommets de l’ensemble en question, puis on décide qu’un lien entre deux nœuds existe dans le graphe projeté selon une métrique relative au graphe biparti. Par exemple, ils partagent plus de \(k\) voisins. D’autres mesures de similarité peuvent s’avérer utiles, comme le coefficient de Jaccard (cardinal de l’intersection des voisinages sur le cardinal de l’union), qui permet de limiter les effets de taille sur la métrique précédente.
Une fois le graphe projeté obtenu, il est possible de procéder à de la détection de communautés. La recommandation d’éléments se fait ensuite sur la base des communautés obtenues, selon des paramètres là encore à choisir :
quels éléments sont retenus (le meilleur de chaque utilisateur, les \(k\) meilleurs, etc.) ;
quel ordre leur est affecté pour un utilisateur donné (votes de la communauté, avec ou sans agrégation, avec ou sans pondération par les poids des liens entre les utilisateurs, etc.).
Des travaux comme [THL13] et [BDFFV14] présentent des synthèses sur les systèmes de recommandation reposant sur une modélisation « graphe » et peuvent prolonger la lecture de ce cours.
Références¶
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., Lefebvre, E. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment 2008 (10), P1000. https://arxiv.org/pdf/0803.0476v2.pdf
Leskovec, J., Rajaraman, A. and J. D. Ullman., Mining of Massive Datasets. Cambridge University Press, New York, NY, USA, 2011. Accessible en version numérique http://www.mmds.org
Shi, J. and Malik, J., Normalized Cuts and Image Segmentation. IEEE PAMI 2000. https://people.eecs.berkeley.edu/~malik/papers/SM-ncut.pdf
Tang, J. and Hu, X. and Liu, H., Social Recommendation: A Review.Social Network Analysis and Mining (SNAM), 2013. http://www.jiliang.xyz/publication/socialrecommendationreview.pdf
Bernardes, D. and Diaby, M. and Fournier, R. and Fogelman-Soulié, F. and Viennet, E., A Social Formalism and Survey for Recommender Systems. SIGKDD Explorations, 16(2), 20–37. http://raphael.fournier-sniehotta.fr/bibliography/files/SocialFormalismSurveyRS-BernardesDiabyFournierViennetFogelman.pdf
Remerciements¶
La plupart des illustrations présentées dans cette page sont tirées des publications de Jean-Loup Guillaume ou de celles des auteurs de Mining of Massive Datasets. Qu’ils soient tous chaleureusement remerciés pour leur travail.


