Cours - Ethique dans la fouille de données¶
[Diapositives du cours : 2 par page] [Diapositives du cours : 1 par page]
Ce chapitre a pour objectif de sensibiliser les personnes qui suivent ce cours aux aspects éthiques des activités de fouille de données (notamment massives). Nous présentons également des métriques permettant d’évaluer dans quelle mesure les prédictions de modèles obtenus à partir de données sont équitables, ainsi que des méthodes permettant d’améliorer l’équité des prédictions.
Dans la séance de travaux pratiques associée des métriques sont évaluées pour différents modèles et une correction a posteriori est appliquée à un modèle pour rendre ses prédictions équitables suivant une de ces métriques.
Pourquoi l’éthique ?¶
En préambule il est utile de rappeler quelques définitions importantes :
Éthique : « Science qui traite des principes régulateurs de l’action et de la conduite morale. » (déf. CNRTL)
Moral : « Qui concerne les règles ou principes de conduite, la recherche d’un bien idéal, individuel ou collectif, dans une société donnée. » (déf. CNRTL)
Équité : « (Principe impliquant l’) appréciation juste, (le) respect absolu de ce qui est dû à chacun. » (déf. CNRTL)
Discrimination : « Traitement différencié, inégalitaire, appliqué à des personnes sur la base de critères variables. » (déf. CNRTL, voir aussi [MMSLG19], [Neil16]))
Loyauté : « [En parlant d’une personne] Fidélité manifestée par la conduite aux engagements pris, au respect des règles de l’honneur et de la probité. » (déf. CNRTL)
Dans toute activité humaine il est important de s’intéresser aux principes régulateurs de l’action et de la conduite morale. Cette préoccupation n’est-elle pas systématique ou ne va-t-elle pas toujours assez loin dans le domaine de la construction et de l’utilisation de modèles prédictifs à partir de données ? Toujours est-il qu’un certain nombre de travers (en anglais c’est souvent le terme bias, plus neutre, qui est employé) sont régulièrement constatés et nous mentionnons ici quelques-uns :
COMPAS (Correctional Offender Management Profiling for Alternative Sanctions) est utilisé aux États-Unis par des juges pour évaluer le risque de récidive et prendre des décisions de libération conditionnelle. Une étude a trouvé que l’outil défavorise les afro-américains par rapport aux caucasiens de profil similaire.
Pour un algorithme qui affiche des annonces d’emploi en sciences, technologie, ingénierie et mathématiques, conçu pour ignorer le genre de la personne qui regarde, une étude a trouvé que les publicités étaient montrées plus rarement aux femmes qu’aux hommes… pour une raison de coût, le public féminin étant une cible publicitaire plus chère que le public masculin.
Un établissement bancaire emploie un outil d’aide à la décision pour accorder ou refuser un crédit. Cet outil exclut toute variable interdite mais exploite un grand nombre d’autres variables. Parmi celles-ci, le code postal (entre autres) qui est très corrélé à la « race » [1] et assez corrélé à la religion.
Une société qui a mis en place un réseau social exploite les informations gratuitement fournies par ses utilisateurs, ainsi que leurs échanges sur le réseau, pour optimiser la vente d’espaces publicitaires. Elle vend également à des tiers des informations concernant ses utilisateurs. En situation de quasi-monopole, cette société peut maximiser ses gains tout en offrant un service basique à la grande majorité des utilisateurs.
Une société de vente de services en ligne adapte au client la tarification de son offre avec pour seul objectif la maximisation de ses bénéfices. Pour cela, elle utilise des données collectées gratuitement auprès de ses clients, ainsi que des données achetées à des data brokers.
Un utilisateur s’informe grâce à un média en ligne. Le site choisit les messages proposés à chaque utilisateur de façon à maximiser le temps de consultation (et donc ses recettes publicitaires), ce qui passe par la maximisation de l’adhésion (et non de la diversité, ni de la véracité). En conséquence, l’utilisateur peut évoluer vers un état d’aliénation dans lequel il perçoit la réalité de façon très déformée.
Un réseau social vend des informations sensibles concernant les utilisateurs (ainsi que les non utilisateurs mentionnés dans les posts des utilisateurs !) à des employeurs actuels ou potentiels, sans que cela soit explicitement mentionné dans les conditions d’utilisation du réseau. Cela a des conséquences sur l’emploi et/ou sur les demandes d’emploi de ces personnes.
Un comparateur de produits et de services modifie l’ordre de présentation des résultats pour privilégier les fournisseurs avec lesquels il a des liens capitalistiques ou, plus largement, des liens d’affaires.
Comment pouvons-nous catégoriser ces travers ? Les points 1, 2 et 3 mettent en évidence des discriminations (absence d’équité). Dans les points 4 et 5 on constate une absence d’équité dans le partage des « gains » entre l’utilisateur d’un service et le fournisseur du service. Enfin, les points 6, 7 et 8 mettent en évidence une absence de « loyauté » (respect de ce qui est explicitement ou implicitement promis) dans la relation entre l’utilisateur et le fournisseur.
A la lecture de cette liste, chacun peut facilement constater que tous ces travers ne semblent pas être d’une gravité équivalente. L’absence de sensibilisation et la banalisation jouent un rôle important dans notre perception de la gravité.
Principaux sujets de préoccupation¶
Pourquoi faut-il s’intéresser à ces problèmes ? Un aspect important est le fait que la législation intègre déjà un certain nombre de règles qui visent à éviter ou à résoudre, du moins dans une certaine mesure, ces problèmes. Et nul n’est censé ignorer la loi, même lorsqu’elle n’est pas systématiquement appliquée.
Au-delà de ce qui a été déjà intégré à la réglementation en vigueur, la préoccupation morale pour les moyens et les finalités d’une action est naturelle. La prise de conscience se manifeste d’ailleurs d’abord comme une préoccupation morale, avant d’inspirer éventuellement une évolution de la réglementation. « La règle de droit peut trouver sa source dans la morale, mais une fois établie en tant que règle, elle s’en sépare pour intégrer le domaine du droit. » (Espace Éthique APHP)
Si la morale n’a pas un caractère universel et immuable, il y a néanmoins des droits fondamentaux reconnus par l’ONU dans la Déclaration universelle des droits de l’homme.
Droits fondamentaux¶
La « Déclaration des droits de l’homme et du citoyen », rédigée en 1789, est un texte fondamental de la Révolution française. Elle a inspiré la Déclaration universelle des droits de l’homme (Organisation des Nations Unies, 10/12/1948), qui prévoit notamment que :
« Tous les êtres humains naissent libres et égaux en dignité et en droits. Ils sont doués de raison et de conscience et doivent agir les uns envers les autres dans un esprit de fraternité. »
« Chacun peut se prévaloir de tous les droits et de toutes les libertés proclamés dans la présente Déclaration, sans distinction aucune, notamment de race, de couleur, de sexe, de langue, de religion, d’opinion politique ou de toute autre opinion, d’origine nationale ou sociale, de fortune, de naissance ou de toute autre situation. »
A l’échelle de l’Union Européenne nous pouvons mentionner la Charte des droits fondamentaux de l’UE (18/12/2000, chap. III, art. 21) dans laquelle nous trouvons : « Est interdite toute discrimination fondée notamment sur le sexe, la race, la couleur, les origines ethniques ou sociales, les caractéristiques génétiques, la langue, la religion ou les convictions, les opinions politiques ou toute autre opinion, l’appartenance à une minorité nationale, la fortune, la naissance, un handicap, l’âge ou l’orientation sexuelle. » Ce que prévoit cette Charte doit être mis en œuvre dans la législation de chaque état membre de l’UE.
Aux États-Unis, la réglementation identifie deux types de problèmes, le disparate treatment qui signifie l’utilisation intentionnelle d’une variable protégée, et le disparate impact, parfois vu comme l’accès à une variable protégée à travers des variables proxy, mais qui considère le problème de l’inéquité de façon bien plus générale. Pour éviter le disparate treatment, la réglementation impose des listes de variables protégées (dont l’utilisation est interdite) pour plusieurs domaines de prise de décision. Le tableau suivant liste les variables protégées par Fair Housing Act (FHA, pour la location d’un logement) et Equal Credit Opportunity Act (ECOA, pour l’accord d’un crédit).
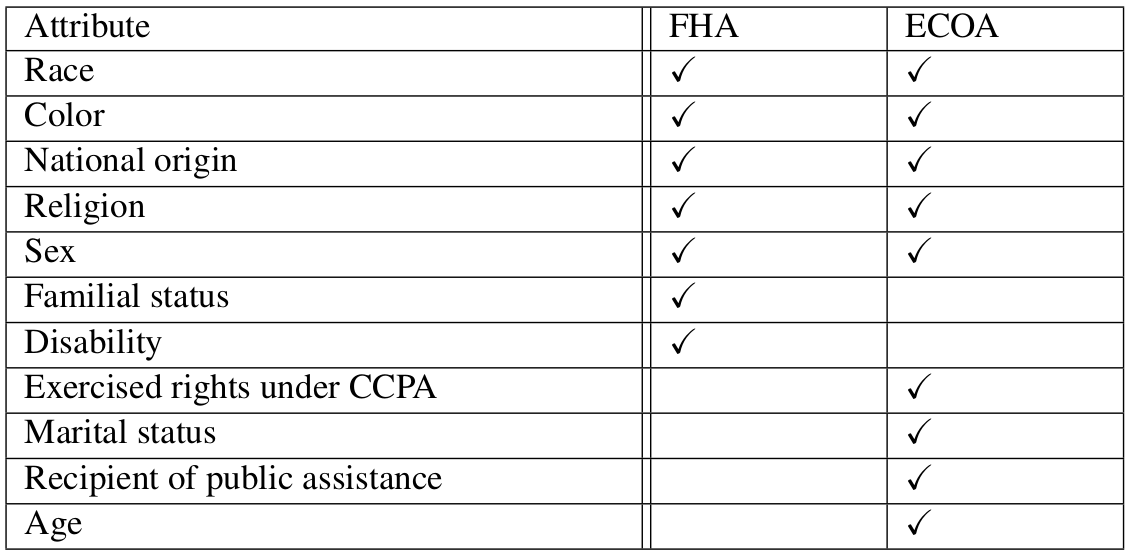
Fig. 133 Variables protégées par Fair Housing Act (FHA) et Equal Credit Opportunity Act (ECOA)¶
Nature des problèmes constatés¶
Les exemples considérés dans l’introduction mettent en évidence une diversité de « travers » ou de problèmes qu’il est nécessaire de catégoriser pour mieux les appréhender. Différentes références, comme par exemple [BHN18], proposent la classification suivante :
Absence d’équité (ou présence de discrimination) dans la prise de décision, qui indique la présence de partialité ou de favoritisme envers un individu ou un groupe sur la base de caractéristiques inhérentes ou acquises. Ce problème est le principal sujet d’étude concernant l’exploitation des données pour la prise de décision et sera également l’objet du reste de ce chapitre. Bien que faisant l’objet de différentes réglementations concernant la prise de décision aussi bien publique que privée, ce problème continue à se manifester de façon parfois flagrante. Nous verrons plus loin que la notion d’équité peut s’exprimer de multiples façons et certaines définitions peuvent être incompatibles entre elles.
Absence de loyauté, qui consiste en un non respect du « contrat », explicite ou implicite, établi par un organisme ou un service avec un utilisateur. Sur ce problème, bien qu’ancien, la prise de conscience est en cours, accélérée parfois par des lanceuses et lanceurs d’alerte. La réglementation est en évolution, par exemple la RGPD impose une explicitation du « contrat » dans l’utilisation des données personnelles.
Absence d’équité dans le partage des « gains » ou avantages issus de l’exploitation des données. Dans ce domaine la prise de conscience est également en cours, accélérée par certains comportements monopolistiques manifestes, mais la réglementation est encore moins avancée.
Plusieurs autres problèmes concernent la prise de décision par des systèmes automatiques (voir par exemple [CERNA]) dans la conduite autonome (par exemple la hiérarchie des valeurs pour le système autonome), la sécurité (par exemple le développement de systèmes d’armement autonomes), etc.
Dans la suite de ce chapitre nous nous intéressons à l’évaluation et au renforcement de l’équité dans la prise de décision qui s’appuie sur un traitement automatique des données.
Biais et discrimination¶
Le sujet le plus abordé à la fois dans les travaux de recherche et dans la réglementation actuelle est la recherche d’équité, où l’équité est comprise comme absence de discrimination (la première signification considérée dans la section précédente).
Historiquement, la préoccupation pour la non discrimination s’est manifestée à travers deux notions :
L’équité « de groupe », qui vise à une forme de parité statistique entre les décisions concernant les différents groupes (définis par les différentes valeurs des attributs protégés [2]: sexe, « race », etc.). Les critères examinés dans la section suivante permettent de mieux appréhender la multiplicité des expressions de la notion de parité statistique.
L’équité « individuelle », qui vise à décider de façon similaire pour des individus qui sont similaires par rapport à l’objectif considéré.
Il est très important de comprendre que des conflits peuvent apparaître dans la mise en œuvre de ces deux notions. Considérons, par exemple, l’emploi d’un outil automatique d’analyse de CV qui sélectionne les candidat.e.s pour des entretiens d’embauche. Supposons que l’employeur constate qu’un groupe protégé [3] est désavantagé par l’outil et décide alors d’équilibrer les taux de sélection pour assurer (ou renforcer) l’équité de groupe. En conséquence, un.e candidat.e d’un groupe non protégé conteste sa non sélection, montrant que des candidat.e.s du groupe protégé, ayant les mêmes qualifications (donc potentiellement similaires par rapport à l’objectif), ont pourtant été sélectionné.e.s (et n’ont donc pas été traité.e.s de façon similaire).
Critères observationnels¶
Nous pouvons maintenant examiner plusieurs critères qui permettent de caractériser quantitativement la notion d’équité. Pour commencer, introduisons quelques notations et des exemples illustratifs.
Notations :
\(X\): variables explicatives disponibles pour la prise de décision ;
\(A\): variable(s) qui représente(nt) explicitement les attributs protégés ; on considère dans la suite que \(A = a\) correspond au groupe « favorisé » et \(A = b\) au groupe « défavorisé » ;
\(Y\): variable expliquée (ou cible) ;
\(R\): score (variable quantitative) employé dans la prise de décision ou éventuellement décision (variable binaire).
Pour mieux comprendre ces notations et les critères définis dans la suite, considérons trois exemples de situations où un outil prédictif est employé pour aider dans la prise de décision :
Accorder un prêt : \(Y\) correspond au remboursement du prêt (\(Y=1\) pour prêt remboursé, \(Y=0\) pour prêt non remboursé), \(R\) correspond au score (si continu) ou à la décision (accorder ou non le prêt) si binaire (\(R=1\) pour accordé, \(R=0\) pour non accordé). On comprend que si \(R=0\) (le prêt n’est pas accordé) alors \(Y\) restera inconnu. Donc, pour construire le modèle comme pour l’évaluer, il faut accepter toutes les candidatures.
Embaucher (éventuellement en période d’essai) : \(Y=1\) si l’employé donne satisfaction, \(Y=0\) sinon. R correspond au score (si continu) ou à la décision (embaucher ou non) si binaire (\(R=1\) pour embauché, \(R=0\) pour non embauché). On comprend que si \(R=0\) (la personne n’est pas embauchée) alors \(Y\) restera inconnu. Donc, pour construire le modèle comme pour l’évaluer, il faut accepter toutes les candidatures.
Libération conditionnelle : \(Y\) correspond à la récidive (\(Y=0\) pour récidive, \(Y=1\) pour non récidive), \(R\) correspond au score (si continu) ou à la décision (libérer ou non) si binaire (\(R=1\) pour libéré, \(R=0\) pour non libéré). On comprend que si \(R=0\) (le détenu n’est pas libéré) alors \(Y\) restera inconnu. Donc, pour construire le modèle comme pour l’évaluer, il faut accepter toutes les candidatures.
Il est important de constater que, dans tous ces exemples, à partir d’une population d’observations, il est très peu probable d’obtenir \(Y \perp\kern-5pt\perp A\), c’est à dire \(P(Y | A) = P(Y)\) (ou \(P(Y=1 | A=a) = P(Y=1 | A=b) = P(Y)\)) !
Trois critères considérés représentatifs (voir par ex. [BHN18]) pour caractériser quantitativement la notion d’équité sont les suivants :
Indépendance (demographic parity) : \(R \perp\kern-5pt\perp A\), c’est à dire le score est indépendant des attributs protégés. Par exemple, pour \(R\) binaire, il y a un même « taux d’acceptation » pour différentes valeurs de \(A\).
Séparation (equalized odds) : \(R \perp\kern-5pt\perp A \,\, | \, Y\), c’est à dire le score et les attributs protégés sont indépendants conditionnellement [4] à la variable cible. Par exemple, pour \(R\) et \(Y\) binaires, les taux de faux positifs et de faux négatifs (voir tableau suivant) ne changent pas pour différentes valeurs de \(A\).
« Suffisance » : \(Y \perp\kern-5pt\perp A \,\, | \, R\), c’est à dire la cible et les attributs protégés sont indépendants conditionnellement au score. Par exemple, pour \(R\) et \(Y\) binaires, les valeurs prédictives (voir tableau suivant ou [5] )positives et les valeurs prédictives négatives ne changent pas pour différentes valeurs de \(A\).
Le tableau suivant présente une matrice de confusion (la variable \(R\) est binaire) avec les définitions associées, notamment celles des taux de faux négatifs et taux de faux positifs, ainsi que celles de la valeur prédictive positive et de la valeur prédictive négative.
Positifs (P: \(Y=1\)) |
Négatifs (N: \(Y=0\)) |
||
|---|---|---|---|
Prédits positifs (PP: \(R=1\)) |
Vrais positifs (VP) |
Faux positifs (FP) |
Valeur prédictive positive = \(\frac{VP}{PP}\) |
Prédits négatifs (PN: \(R=0\)) |
Faux négatifs (FN) |
Vrais négatifs (VN) |
Valeur prédictive négative = \(\frac{VN}{PN}\) |
Taux faux négatifs TFN = \(\frac{FN}{P}\) (TFN = 1-TVP) |
Taux faux positifs TFP = \(\frac{FP}{N}\) (TFP = 1-TVN) |
Critère d’indépendance¶
Le critère d’équité le plus souvent considéré est le critère d’indépendance qui peut être défini par une des conditions suivantes :
Dans un cas général, l’information mutuelle entre \(R\) et \(A\) doit être nulle, \(I(A;R)=0\).
Pour \(R\) binaire, \(P(R=1|A=a) = P(R=1|A=b)\) (\(R=1\) désigné en général par « acceptation »).
Il est important de noter que le critère d’indépendance présente des insuffisances manifestes. D’abord, si \(Y\) n’est pas indépendant de \(A\), ce qui est malheureusement le cas habituel, alors le score « parfait » (d’un point de vue de la qualité de prédiction) qui serait \(R = Y\) ne peut pas satisfaire le critère d’indépendance \(R \perp\kern-5pt\perp A\). Pour satisfaire le critère d’indépendance il faut s’écarter, potentiellement beaucoup, du score « parfait » !
Par ailleurs, le respect du critère d’indépendance ne suffit pas à garantir la non discrimination. Pour s’en rendre compte, considérons l’exemple suivant : on s’assure d’un taux d’acceptation identique dans les groupes \(a\) et \(b\) mais on applique une sélection attentive (sur la base du score \(R\)) dans le groupe \(a\) et un choix aléatoire (mais en s’assurant d’un taux d’acceptation identique) dans le groupe \(b\). La conséquence est que les accepté.e.s du groupe \(b\) obtiennent vraisemblablement des résultats généralement inférieurs aux acceptés du groupe \(a\), ce qui peut être utilisé a posteriori pour privilégier le groupe \(a\) !
Afin de mieux percevoir la signification du critère d’indépendance nous pouvons l’expliciter pour les exemples considérés :
La probabilité d’accorder un prêt (ou la proportion de membres du groupe, candidats à un prêt, auxquels le prêt est accordé) est la même pour le groupe favorisé (\(A=a\)) et pour le groupe défavorisé (\(A=b\)).
La probabilité d’embaucher (ou la proportion de membres du groupe, candidats à l’embauche, qui ont été embauchés) est la même pour le groupe favorisé (\(A=a\)) et pour le groupe défavorisé (\(A=b\)).
La probabilité de libération conditionnelle (ou la proportion de membres du groupe, candidats à une libération, qui ont été libérés) est la même pour le groupe favorisé (\(A=a\)) et pour le groupe défavorisé (\(A=b\)).
Si le critère d’indépendance ne peut pas être parfaitement satisfait, il est envisageable de chercher à satisfaire une version « relaxée » de ce critère. Ainsi, avec \(\epsilon > 0\) mais proche de \(0\), en considérant que le groupe \(A = b\) est le groupe protégé, des conditions relaxées peuvent s’exprimer sous une des formes suivantes :
Ecart de disparité faible : \(P(R=1|A=b) \geq P(R=1|A=a)-\epsilon\).
Ratio de disparité démographique proche de 1 : \(\frac{P(R=1|A=b)}{P(R=1|A=a)} \geq 1-\epsilon\).
Information mutuelle entre \(A\) et \(R\) proche de 0 : \(I(A;R) \leq \epsilon\).
Nous avons constaté que s’il n’y avait pas d’indépendance entre \(Y\) et \(A\) (et c’est le cas le plus fréquent) alors le score \(R\) « parfait » qui est \(R = Y\) ne pouvait pas satisfaire la condition d’indépendance. Cette condition peut être considérée non cohérente avec l’absence d’indépendance entre \(Y\) et \(A\). Un autre critère, comme le critère de séparation ou le critère de suffisance (décrits dans la suite), peut alors être mieux adapté.
Critère de séparation¶
Le mot « séparation » dans le nom de ce critère vient du fait que dans le modèle graphique associé \(Y\) sépare \(R\) de \(A\).
L’intuition pour ce critère est que l’absence d’indépendance entre \(Z\) et \(A\) peut être acceptable (lorsque \(Y\) et \(A\) ne sont pas indépendants) mais pas au-delà de ce qui est justifié par la cible \(Y\).
Pour \(R\) et \(Y\) binaires, le critère de séparation s’exprime sous la forme suivante :
\(P(R=1|Y=1,A=a) = P(R=1|Y=1,A=b)\) (même taux de vrais positifs) et
\(P(R=1|Y=0,A=a) = P(R=1|Y=0,A=b)\) (même taux de faux positifs).
Ce critère est donc un critère de l’égalisation des chances (equalized odds). Son application pratique présente une difficulté importante : pour l’évaluer il faut avoir accès à la valeur de \(Y\) or, lorsque la règle de sélection est appliquée, cela est possible seulement si \(R=1\).
Afin de mieux percevoir sa signification, nous pouvons expliciter le critère de séparation pour les trois exemples considérés :
La probabilité d’obtenir un score qui correspond à accorder un prêt (\(R=1\)) à un membre du groupe favorisé (\(A=a\)) qui remboursera le prêt (\(Y=1\)) est la même que pour un membre du groupe défavorisé (\(A=b\)) qui remboursera le prêt, c’est à dire parmi ceux qui rembourseront le prêt aucun groupe n’est favorisé dans la décision d’accorder le prêt (le taux de « perte de chance » par non accord du prêt alors qu’il aurait été remboursé est le même dans les deux groupes).
La probabilité d’obtenir un score qui correspond à embaucher (\(R=1\)) un membre du groupe favorisé (\(A=a\)) qui donnera satisfaction (\(Y=1\)) est la même que pour un membre du groupe défavorisé (\(A=b\)) qui donnera satisfaction, c’est à dire parmi ceux qui donnent satisfaction aucun groupe n’est favorisé dans la décision d’embauche (le taux de « perte de chance » par non embauche alors qu’il aurait donné satisfaction est le même dans les deux groupes).
La probabilité d’obtenir un score qui correspond à libérer (\(R=1\)) un détenu membre du groupe favorisé (\(A=a\)) qui ne récidivera pas (\(Y=1\)) est la même que pour un membre du groupe défavorisé (\(A=b\)) qui ne récidivera pas, c’est à dire parmi ceux qui ne récidiverons pas aucun groupe n’est favorisé dans la décision de libération conditionnelle (le taux de « perte de chance » par non libération alors qu’il n’y aurait pas eu récidive est le même dans les deux groupes).
Comme le critère d’indépendance, le critère de séparation (ou de l’égalité des chances) peut aussi être relaxé ; les conditions relaxées peuvent s’exprimer sous une des formes suivantes :
Contrainte sur le seul taux de faux négatifs quand « positif » signifie opportunité (par exemple embauche), donc les faux négatifs sont les opportunités non accordées.
Contrainte sur le seul taux de faux positifs quand « positif » signifie pénalité (par exemple maintien en prison car récidive prédite), donc les faux positifs sont les pénalités injustifiées.
Seuil \(> 0\) sur l’écart entre le taux considéré pour \(A=a\) et celui pour \(A=b\).
Critère de « suffisance »¶
Pour le critère de suffisance, dans le modèle graphique associé \(R\) sépare \(Y\) de \(A\). La signification est que la valeur prédictive ne doit pas dépendre du groupe (valeur de \(A\)). Pour \(R\) et \(Y\) binaires, cela revient à :
\(P(Y=1|R=1,A=a) = P(Y=1|R=1,A=b)\) : même valeur prédictive positive, et
\(P(Y=0|R=0,A=a) = P(Y=0|R=0,A=b)\) : même valeur prédictive négative.
Comme pour le critère de séparation, l’évaluation du critère de suffisance exige un accès à la valeur de \(Y\) or, lorsque la règle de sélection est appliquée, cela est possible seulement si \(R=1\).
Afin de mieux percevoir la signification du critère de suffisance, nous pouvons l’expliciter pour les trois exemples considérés :
La probabilité de rembourser le prêt (\(Y=1\)) est la même pour les membres du groupe favorisé (\(A=a\)) qui ont obtenu le score qui correspond à l’accord d’un prêt (\(R=1\)) que pour les membres du groupe défavorisé (\(A=b\)) qui ont obtenu le score qui correspond à l’accord d’un prêt, c’est à dire que parmi ceux à qui le prêt a été accordé la même proportion le remboursera dans le groupe favorisé et dans le groupe défavorisé (le score \(R\) est également prédictif de la cible \(Y\) dans les deux groupes).
La probabilité de donner satisfaction (\(Y=1\)) est la même pour les membres du groupe favorisé (\(A=a\)) qui ont obtenu le score qui correspond à l’embauche (\(R=1\)) que pour les membres du groupe défavorisé (\(A=b\)) qui ont obtenu le score qui correspond à l’embauche, c’est à dire que parmi ceux qui ont été embauchés la même proportion donnera satisfaction dans le groupe favorisé et dans le groupe défavorisé (le score \(R\) est également prédictif de la cible \(Y\) dans les deux groupes).
La probabilité de ne pas récidiver (\(Y=1\)) est la même pour un détenu membre du groupe favorisé (\(A=a\)) qui a été libéré (\(R=1\)) est la même que pour les membres du groupe défavorisé (\(A=b\)) qui a été libéré, c’est à dire parmi ceux qui ont été libérés la même proportion récidivera dans le groupe favorisé et dans le groupe défavorisé (le score \(R\) est également prédictif de la cible \(Y\) dans les deux groupes).
Le lien de ce critère avec la notion statistique de calibration peut également permettre de mieux comprendre ce critère :
Définition de la calibration : le score \(R\) est calibré si, pour toute valeur \(r \in [0, 1]\) que peut prendre \(R\), \(P(Y=1|R=r) = r\), c’est à dire que parmi les observations de score \(r\), une fraction égale à \(r\) sont positives (\(Y=1\)). Par calibration par groupe on entend le fait que la condition de calibration soit satisfaite pour tout groupe défini par une valeur différente de \(A\), c’est à dire \(P(Y=1|R=r,A=a) = P(Y=1|R=r,A=b) = r\).
Le lien entre calibration est suffisance est le suivant : la calibration par groupe implique la suffisance, la suffisance implique la calibration par groupe à une transformation monotone de score près.
Relations entre les trois critères¶
Les relations d’incompatibilité mentionnées ici sont valables dans le cas, malheureusement typique, où \(A\) (l’attribut protégé) et \(Y\) (la variable expliquée ou cible) ne sont pas indépendantes, c’est à dire le taux de positifs (\(Y=1\)) est différent entre les groupes définis par les différentes valeurs de l’attribut protégé \(A\).
Relation entre le critère d’indépendance et le critère de séparation : si \(A\) et \(Y\) ne sont pas indépendantes et \(Y\) est binaire, alors \(R \perp\kern-5pt\perp A\) et \(R \perp\kern-5pt\perp A \,\, | \, Y\) ne peuvent pas être valables simultanément.
Relation entre le critère d’indépendance et le critère de suffisance : si \(A\) et \(Y\) ne sont pas indépendantes, alors \(R \perp\kern-5pt\perp A\) et \(Y \perp\kern-5pt\perp A \,\, | \, R\) ne peuvent pas être valables simultanément.
Relation entre le critère de séparation et le critère de suffisance : si \(A\) et \(Y\) ne sont pas indépendantes et toutes les probabilités jointes \((A,R,Y)\) sont positives, alors \(R \perp\kern-5pt\perp A \,\, | \, Y\) et \(Y \perp\kern-5pt\perp A \,\, | \, R\) ne peuvent pas être valables simultanément.
Nous pouvons donc constater que, dans les conditions courantes (\(A\) et \(Y\) ne sont pas indépendantes) plusieurs critères ne peuvent pas être satisfaits simultanément de façon stricte. Il est en revanche envisageable de rechercher des compromis grâce aux relaxations mentionnées pour chacun des trois critères.
Typologie et sources des biais¶
Le terme « biais » (bias) est fréquemment employé ([BHN18], [CERNA], [MMSLG19], [Neil16]) dans le contexte de travaux qui abordent les problèmes d’absence d’équité ou de discrimination dans la prise de décision aidée par des algorithmes. Le sens qu’on peut retenir ici est celui de « déformation, travers » (déf. CNRTL). Mais la signification de ce terme est sujet à confusions. En statistique, par biais on entend en général un écart systématique entre l’espérance de la valeur estimée et la vraie valeur. En apprentissage statistique (machine learning), le biais correspond à une erreur systématique souvent attribuée à des hypothèses erronées, par exemple l’emploi d’une famille de modèles de capacité insuffisante. Dans le contexte d’une discussion concernant l’absence d’équité, par biais on entend des disparités démographiques légalement répréhensibles ou du moins moralement discutables dans la prise de décision basée sur des algorithmes.
D’où proviennent ces disparités ? D’abord, il est indéniable que des disparités démographiques sont présentes dans la société, pour des raisons historiques ou sociales. Ces disparités se retrouvent naturellement dans les données recueillies et engendrent donc des disparités dans les modèles décisionnels (aussi bien algorithmiques qu’humains) dans la mesure où ces modèles sont développés à partir de données. Un cercle vicieux peut alors se former : les disparités existantes se retrouvent dans les données recueillies et, en conséquence, dans les modèles obtenus à partir de ces données, les décisions prises par ces modèles (ou celles que ces modèles aident à prendre) ont un impact sociétal et peuvent ainsi contribuer à perpétuer les disparités existantes. Il est donc important de pouvoir éviter le transfert des disparités des données vers les modèles ou, du moins, de pouvoir corriger les modèles a posteriori.
Parmi les mécanismes qui permettent aux disparités démographiques de se retrouver dans les données, un mécanisme important concerne la définition et la mesure des variables, notamment des variables cibles (variables expliquées). Par exemple, la variable récidive ne pouvant être mesurée directement (la récidive peut rester cachée, on ne la connaît que lorsqu’elle est détectée), c’est souvent la variable arrestation qui s’y substitue, or celle-ci est malheureusement soumise à des disparités démographiques dues souvent à des biais humains.
Il est important de noter que les disparités dans les données ne sont pas toutes issues de disparités démographiques historiques ou ne se réduisent pas à celles-ci. La méthode employée pour la constitution des bases de données, comme l’utilisation d’un échantillonnage de convenance (on choisit l’échantillon qui est le plus facilement accessible), peut introduire des disparités ou renforcer celles déjà présentes dans la population. Par exemple, pour minimiser le coût d’un sondage on l’applique là où il est plus facile d’avoir des réponses en grand nombre, c’est à dire là où sont présentes les catégories majoritaires.
Les disparités présentes dans les données peuvent être tranférées aux modèles par plusieurs mécanismes différents :
Le premier mécanisme est l’action directe, c’est à dire l’inclusion de variables protégées dans les variables explicatives employées. Cela peut être explicitement prohibé par la législation dans certains cas et certains pays (cas de disparate treatment aux Etats-Unis).
Le second mécanisme est l’action par l’intermédiaire de proxy, c’est à dire de variable(s) de substitution qui remplace(nt) une variable critique non observable ou non mesurable ou protégée. Un exemple classique aux États-Unis est l’emploi du zip code comme proxy de la « race ». Suivant les variables employées, le lien entre proxy et variable protégée peut être plus difficile à mettre en évidence.
Action par l’intermédiaire de disparités dans les données qui engendrent des corrélations entre variables explicatives « anodines » et la variable protégée. En effet, l’absence de proxy clair ne signifie pas que l’attribut protégé est inaccessible (et encore moins qu’il n’y a pas de transfert de disparités). Cumuler un nombre suffisant de variables « anodines » (chacune peu corrélée à la variable protégée) peut suffire pour estimer assez bien la valeur de la variable protégée, comme le montre l’illustration suivante. Nous sommes ici dans un cas de disparate impact plus difficile à caractériser que l’emploi de proxy.
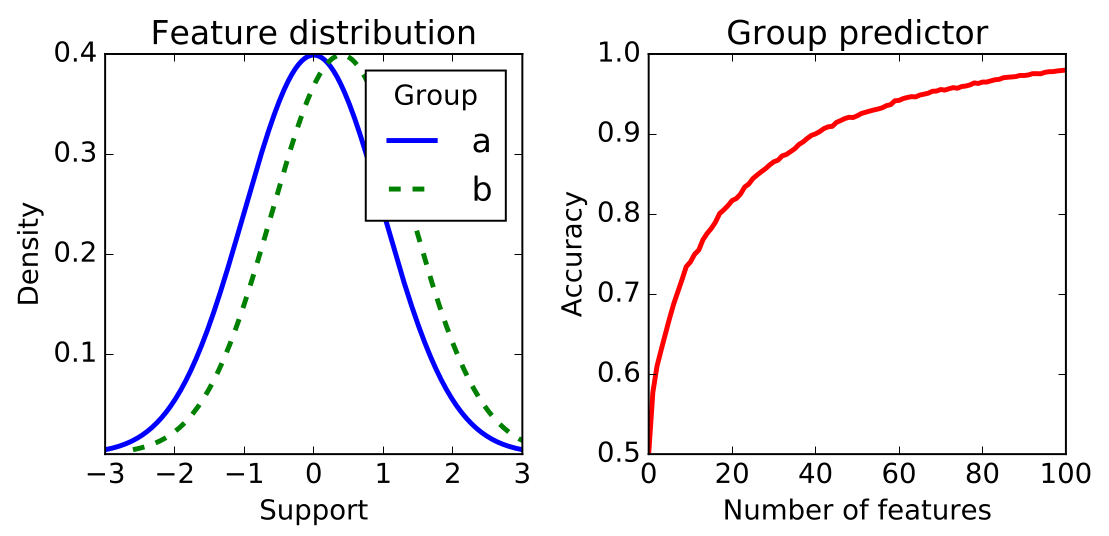
Fig. 134 A partir d’un nombre suffisant de variables légèrement corrélées à l’attribut protégé (distributions légèrement différentes pour les deux valeurs de l’attribut protégé) il est possible de (très) bien prédire la valeur de l’attribut protégé (donc de l’imputer si absente). Illustration issue de [BHN18].¶
Détecter l’iniquité¶
Pour pouvoir agir contre la discrimination (ou l’absence d’équité, ou l’iniquité) il est d’abord nécessaire de la détecter. La discrimination étant présente dans la décision humaine depuis toujours, différentes techniques ont été mises au point pour la mettre en évidence :
Les tests d’aveuglement (blinding) consistent à vérifier la non prise en compte des attributs protégés (ainsi que, parfois, celle des proxies qui permettraient de les deviner de façon trop évidente), sans imposer un contrôle des autres variables.
Les audits comportent également des tests d’aveuglement mais en contrôlant les autres variables. En effet, il faut pouvoir comparer les résultats obtenus avec différentes valeurs pour l’attribut protégé « toutes choses égales par ailleurs ». Souvent, les combinaisons d’attributs résultant de cette contrainte ne correspondent pas à des cas rééls et cela peut rendre les audits peu applicables.
Révéler l’arbitraire dans les décisions : il s’agit de mettre en évidence le caractére non systématique de la procédure de prise de décision, notamment en révélant des relations entre la décision (ou le score sur lequel s’appuie la décision) et des facteurs arbitraires qui ne devraient pas intervenir dans la prise de décision.
Tests basés sur les issues (outcomes) \(Y\) lorsqu’elles sont disponibles (par exemple, \(Y\) peut être le défaut ou non du remboursement d’un prêt, et \(R\) le score sur la base duquel le prêt est accordé ou non). Nous pouvons trouver :
Le test de suffisance (\(Y \perp\kern-5pt\perp A \,\, | \, R\)) consiste à vérifier, pour des candidats dont le score \(R\) est dans un intervalle étroit, s’il y a un même taux de \(Y=1\) pour chaque valeur de l’attribut protégé \(A\) (chaque groupe). Le test est difficile à appliquer pour le score dans un intervalle large car \(Y\) n’est pas disponible si \(R\) est trop bas.
En l’absence d’accès au score \(R\) il est possible d’appliquer un test de parité de prédiction, en vérifiant si le taux de \(Y=1\) est le même pour les candidats classés favorablement (\(\hat{Y}=1\)) dans chaque groupe.
Le test de séparation (\(R \perp\kern-5pt\perp A \,\, | \, Y\)) est difficile à appliquer car en général \(Y\) est observé seulement pour \(\hat{Y}=1\). Le test est donc possible seulement si on peut évaluer \(Y\) aussi pour \(\hat{Y}=0\).
Quelles sont les différences majeures entre la décision humaine et la décision qui s’appuie sur un traitement algorithmique ? Quelles sont les conséquences sur l’adéquation des tests précédents au cas algorithmique ? La décision humaine peut facilement être non aveugle (si les valeurs des attributs protégées ne sont pas supprimées des donnés en amont), ainsi que non systématique (arbitraire), en revanche la décision humaine (non aidée par un algorithme) ne peut pas traiter un grand nombre de variables pour imputer les valeurs manquantes d’un attribut protégé. En revanche, la décision algorithmique est systématique, il est possible d’exclure a priori les attributs protégés (et les proxies évidents), en revanche un algorithme peut inférer les valeurs des attributs protégés à partir des autres variables « anodines ». En conséquence, pour la décision qui s’appuie sur un traitement algorithmique :
Les tests d’aveuglement sont peu pratiqués car les attributs protégés peuvent être exclus a priori. Aussi, le blinding est peu utile car les attributs protégés peuvent (dans une certaine mesure, suivant l’application et les données) être inférés des autres variables individuellement anodines.
Révéler l’arbitraire n’a pas d’intérêt à première vue car une procédure algorithmique est en principe systématique. En revanche, un excès de variables explicatives peut éventuellement permettre (présence de surapprentissage) de trouver prédictifs des facteurs arbitraires, il est donc indispensable de pouvoir détecter le surapprentissage.
Les critères observationnels — la parité démographique ou la parité des taux d’erreur ou la calibration — sont potentiellement applicables, avec les réserves mentionnées lorsque nous les avons étudiés. Les résultats de l’évaluation de ces critères est toutefois à considérer avec précaution, comme nous le verrons tout de suite. Dans tous les cas, ces critères restent utiles pour motiver une analyse plus approfondie des mécanismes d’apparition des iniquités.
Certaines précautions doivent être prises dans l’interprétation des résultats de tests de discrimination. Les exemples suivants montrent qu’avant de tirer des conclusions définitives à partir des tests il est nécessaire de comprendre le mécanisme exact qui mène au résultat d’un test dans chaque situation.
Des moteurs de recherche généralistes ont été accusés de personnaliser les résultats même lorsque’on leur demande explicitement de ne pas les personnaliser. Ainsi, des recherches équivalentes donneraient des résultats qui dépendent des recherches antérieures, renforçant ainsi les croyances de la personne qui cherche. Une analyse plus approfondie a mis en évidence que les requêtes considérées « équivalentes » n’étaient pas identiques, chaque personne employait des termes spécifiques suivant ses croyances et ces termes orientaient différemment les résultats de recherche.
Un test a mis en évidence la fait qu’site de vente en ligne qui a aussi des magasins « en dur » proposait des réductions plus fortes pour certains zip codes que pour d’autres (on rappelle que dans certains endroits le zip code peut être un proxy pour « race »). Un examen plus approfondi des raisons a permis de montrer que la réduction augmentait (naturellement) avec la concurrence locale autour du zip code, or cette concurrence était plus forte là où le pouvoir d’achat local était supérieur.
Supprimer ou réduire l’iniquité¶
Plusieurs approches générales ont été proposées dans la littérature pour supprimer ou réduire l’iniquité (certaines formulations ci-dessous sont adaptées au critère d’indépendance mais les mêmes approches s’appliquent à d’autres critères) :
Le prétraitement vise à transformer la représentation des données pour enlever le biais (par exemple, pour la rendre indépendante des attributs protégés) et faciliter ainsi l’apprentissage de modèles équitables. Un prétraitement exige l’accès complet aux données employées pour apprendre et évaluer le modèle, ainsi qu’à l’attribut protégé. Un avantage important de cette approche est que, en enlevant les biais des données, il n’y a aucune restriction sur les méthodes de modélisation appliquées en aval.
L’inclusion du respect de la contrainte dans le processus d’optimisation qui permet d’obtenir le modèle décisionnel. Cette approche exige également l’accès aux données, à l’attribut protégé et à la procédure d’apprentissage. Par ailleurs, l’emploi de cette approche impose des contraintes sur les familles de modèles utilisées et sur les procédures d’optimisation.
Le post-traitement vise à ajuster un modèle décisionnel déjà obtenu pour que ses décisions respectent le critère d’équité considéré. Cette approche ne nécessite pas l’accès aux données ou à la procédure d’apprentissage (car le modèle est déjà appris), en revanche exige l’accès à l’attribut protégé car ce sont ses valeurs qui permettent de bien appliquer les corrections. Aussi, cette approche peut s’appliquer à tout modèle, y compris aux modèles de type « boîte noire ».
Il est important d’observer que toutes les approches qui visent à supprimer ou à réduire l’iniquité exigent l’accès à l’attribut protégé (même si le modèle est au départ développé sans accès à l’attribut protégé).
Considérons maintenant, très brièvement, quelques exemples de méthodes permettant de supprimer ou réduire l’iniquité :
Suivant l’approche du prétraitement :
Compléter les données : il est parfois possible de compléter la collecte de données en suivant des plans d’expérience pour réduire les disparités présentes dans les données.
Redressement de l’échantillon (par exemple en augmentant les pondérations des individus dans les populations sous-représentées) ou ré-échantillonnage (sous/sur-échantillonnage suivant que le groupe est sur ou sous-représenté, génération par interpolation dans les groupes sous-représentés).
Suivant l’approche de l’inclusion du respect de la contrainte dans le processus d’apprentissage :
Le processus d’optimisation tient compte en général du risque empirique et de termes de régularisation, en introduisant un terme supplémentaire de « coût d’iniquité » (suivant le critère d’équité considéré) il est possible d’obtenir un compromis entre performance et respect de l’équité.
Suivant l’approche du post-traitement :
Lorsque le modèle fournit un score quantitatif, modification sélective des seuils de décision, en les diminuant pour les groupes protégés et en les augmentant pour les groupes privilégiés (voir par exemple [HPS16]).
Lorsque le modèle fournit directement une prédiction binaire \(\hat{Y}\), par randomisation partielle des prédictions il est possible de respecter un critère observationnel d’équité en diminuant le moins possible les performances de prédiction, voir par ex. [HPS16]. Cette approche est mise en œuvre dans cette séance de travaux pratiques associée à ce cours.
Solon Barocas, Moritz Hardt, and Arvind Narayanan. Fairness and Machine Learning Limitations and Opportunities. 2018.
Moritz Hardt, Eric Price, and Nati Srebro. Equality of opportunity in supervised learning. In D. Lee, M. Sugiyama, U. Luxburg, I. Guyon, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 29. Curran Associates, Inc., 2016.
