Travaux pratiques - Détection et correction des disparités¶
Références externes utiles :
L’objectif de cette séance de TP est d’illustrer, à travers un exemple issu de données réelles, la problématique de la détection et de la correction des inéquités (des disparités) présentes dans les prédictions des modèles.
Récupération des données¶
Nous travaillerons de nouveau, dans cette séance de travaux pratiques, sur les données Adult de la base UCI. Ces données ont été employées pour prédire si le revenu annuel d’un individu dépasse 50 k$ (en 1996). Regardez ce site pour une description des variables présentes. Les données n’ont pas été pré-traitées au préalable, comme lors de l’utilisation antérieure.
Pour préparer les répertoires et télécharger ces données générées en amont, ouvrez une fenêtre terminal et entrez les commandes suivantes :
%%bash mkdir -p tpequite/data wget -nc http://cedric.cnam.fr/vertigo/Cours/RCP216/docs/adult.csv -P tpequite/data/ pyspark
Sous Windows, créez le répertoire tpequite et le sous-répertoire data, téléchargez le fichier de données dans le sous-répertoire data, ouvrez une fenêtre invite de commandes, allez dans le répertoire tpequite que vous avez créé et lancez pyspark.
Pré-traitement et examen des données¶
Nous utilisons la bibliothèque Pandas pour lire les données à partir d’un fichier du système de fichier centralisé dans un dataframe Pandas et lui appliquer quelques transformations simples.
import pandas as pd
import numpy as np
pandasDF = pd.read_csv('tpequite/data/adult.csv')
pandasDF.head()
Quelles sont les variables qui décrivent les données :
pandasDF.columns
Remplacer le symbole ? utilisé pour les valeurs manquantes du fichier d’origine par np.nan (not a number de Numpy) :
pandasDF[pandasDF == '?'] = np.nan
pandasDF.info()
Les seules variables qui présentent des valeurs manquantes sont les variables nominales workclass, occupation et native.country. Plutôt que supprimer les observations à valeurs manquantes, nous décidons d’estimer les valeurs manquantes par le mode (la valeur la plus fréquente) de chaque variable :
# Impute missing values with mode
for col in ['workclass', 'occupation', 'native.country']:
pandasDF[col].fillna(pandasDF[col].mode()[0], inplace=True)
pandasDF.info()
Question :
Pouvons-nous faire la même opération dans Spark ? Regardez la documentation.
Correction :
Oui, comme indiqué dans description de Imputer de l’API de Spark en Python. Il faudra convertir d’abord le dataframe Pandas en DataFrame Spark (voir plus loin).
Il faut noter que certaines méthodes de modélisation prédictive peuvent toutefois traiter des observations à valeurs manquantes.
Nous pouvons maintenant afficher des statistiques simples concernant les données (la même opération sera faite plutôt avec Spark pour des données très volumineuses) :
pandasDF.describe().T # .T indique la transposition
Nous pouvons enfin convertir le dataframe Pandas (structure de données centralisée) en DataFrame Spark (structure de données distribuées) :
# Renommer les colonnes dont le nom contient .
columns = {"education.num": "educationnum", \
"marital.status": "maritalstatus", \
"capital.gain": "capitalgain", \
"capital.loss": "capitalloss", \
"hours.per.week": "hoursperweek", \
"native.country": "nativecountry"}
sparkDF = spark.createDataFrame(pandasDF)
for key, value in columns.items():
sparkDF = sparkDF.withColumnRenamed(key, value)
sparkDF.printSchema()
sparkDF.show()
Formulation du problème et analyse des disparités présentes¶
Les données Adult d’origine ont été employées pour prédire si le revenu annuel d’un individu dépasse 50 k$ ou non (en 1996). Afin de situer ces données dans un contexte d’analyse et de correction des disparités, nous considérerons qu’une institution financière cherche à développer un outil d’aide à la décision qui vise à prédire si un prêt serait remboursé ou non ; pour cela, elle s’appuie sur les données Adult dans lesquelles la variable income observée est assimilée au remboursement du prêt (income \(\geq 50k$ \leftrightarrow\) remboursement, income \(< 50k$ \leftrightarrow\) défaut de remboursement) ; la valeur de income prédite par le modèle à mettre au point sert à prendre la décision d’accorder ou non le prêt (prêt accordé si income prédit \(\geq 50k$\), prêt refusé si income prédit \(< 50k$\)).
Nous examinerons donc les variables génériques suivantes :
\(X\) : variables prédictives employées dans la modélisation ;
\(A\) : attribut protégé, c’est à dire qui ne doit pas avoir d’impact sur la prise de décision ;
\(Y\) : variable cible (outcome), ici remboursement ou défaut (binaire) ;
\(\hat{Y}\) ou \(R\) : prédiction du modèle sous la forme d’une prédiction binaire (\(\hat{Y}\)) ou d’un score (\(R\)).
Cette formulation est un simple exercice à but pédagogique et ne prétend pas avoir un quelconque rapport avec la façon dont une institution financière procède réellement pour aboutir à des décisions d’accorder ou non un prêt.
Question :
Parmi les variables présentes dans les données, lesquelles sont protégées suivant Equal Credit Opportunity Act (ECOA) ?
Correction :
Les variables présentes dans les données Adult mais protégées suivant la réglementation Equal Credit Opportunity Act (ECOA, voir la liste complète dans le cours ou sur Internet) sont : age, maritalstatus, race, sex, nativecountry.
Afin de poursuivre l’analyse, nous faisons d’abord l’importation des bibliothèques nécessaires :
from pyspark.ml.feature import VectorAssembler
from pyspark.ml.feature import StringIndexer, VectorIndexer
from pyspark.ml.classification import GBTClassifier
from pyspark.ml import Pipeline
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
Ensuite, nous appliquons un codage particulier aux variables nominales : chaque modalité est représentée par une valeur entière spécifique. Attention, ce type de codage peut être employé pour l’utilisation des méthodes de modélisation à base d’arbres de décision (ou de forêts d’arbres), mais pas pour des méthodes comme les SVM ou les réseaux de neurones (pour lesquelles il faudra employer plutôt un codage one-hot).
# Variables nominales : colonnes qui contiennent des données de type string
stringColumns = [c for c, t in sparkDF.dtypes if t.startswith('string')]
print(stringColumns)
# Valeurs index pour variables nominales : une modalité est représentée par son index plutôt que par son nom
for strCol in stringColumns:
labelIndexer = StringIndexer(inputCol =strCol, \
outputCol='indexed'+strCol).fit(sparkDF)
sparkDF = labelIndexer.transform(sparkDF)
sparkDF.printSchema()
Disparités dans les données¶
Avant d’examiner les disparités présentes dans les prédictions de différents modèles, regardons si des disparités sont présentes dans les données de départ. Nous pouvons examiner le taux de « positifs » (income >= 50k, ou indexedincome = 1.0) pour les deux valeurs de l’attribut protégé sex :
sparkDF.groupBy("sex").count().show() # effectif de chaque modalité de 'sex'
sparkDF.groupBy("sex").avg("indexedincome").show() # taux de positifs (income >= 50k)
et constater ainsi que la variable cible (outcome) \(Y\) n’est pas indépendante de l’attribut protégé \(A\) = sex.
Même analyse pour les valeurs de l’attribut protégé race :
sparkDF.groupBy("race").count().show() # effectif de chaque modalité de 'race'
sparkDF.groupBy("race").avg("indexedincome").show() # taux de positifs (income >= 50k)
et même constat d’absence d’indépendance entre la variable cible \(Y\) et l’attribut protégé \(A\) = race.
Question :
Examinez la relation entre la variable cible \(Y\) et chacun des attributs protégés maritalstatus, nativecountry. Que faudrait-il faire pour pouvoir traiter de la même façon la variable continue age ?
Correction :
sparkDF.groupBy("maritalstatus").count().show() # effectif de chaque modalité de 'maritalstatus'
sparkDF.groupBy("maritalstatus").avg("indexedincome").show() # taux de positifs (income >= 50k)
sparkDF.groupBy("nativecountry").count().show() # effectif de chaque modalité de 'nativecountry'
sparkDF.groupBy("nativecountry").avg("indexedincome").show() # taux de positifs (income >= 50k)
Pour age il est possible de définir des modalités en découpant le domaine de variation en intervalles, voir par ex. Bucketizer ou QuantileDiscretizer.
Modèle obtenu avec tous les attributs¶
Nous considérons d’abord un modèle prédictf obtenu avec toutes les variables, qui sera ensuite comparé à un modèle obtenu en excluant les variables protégées suivant la réglementation ECOA. La comparaison portera à la fois sur la performance brute (accuracy globale) et sur les disparités.
L’appel au VectorAssembler est nécessaire pour mettre les données sous une forme directement exploitable :
featureAssemblerFull = VectorAssembler(inputCols = \
['age', 'indexedworkclass', 'fnlwgt', \
'indexededucation', 'educationnum', \
'indexedmaritalstatus', 'indexedoccupation', \
'indexedrelationship', 'indexedrace', \
'indexedsex', 'capitalgain', 'capitalloss', \
'hoursperweek', 'indexednativecountry'], \
outputCol = 'indexedFeaturesAll')
sparkDFassembledFull = featureAssemblerFull.transform(sparkDF)
sparkDFassembledFull.printSchema()
Une séparation aléatoire simple est faite entre des données d’apprentissage et des données de test. Pour rendre l’expérience répétable, nous fixons à 100 la valeur de seed pour le générateur de nombres pseudo-aléatoires :
(trainingDataFull, testDataFull) = sparkDFassembledFull.randomSplit([0.7, 0.3], 100)
La méthode de modélisation choisie est Gradient Boosted Trees (GBT) qui permet de mélanger directement variables quantitatives et variables nominales sans pré-traitements supplémentaires. Par ailleurs, GBT fait partie des méthodes qui obtiennent les meilleurs résultats sur ce problème de prédiction. Noter que nous ne faisons pas de recherche de valeurs optimales pour les hyperparamètres. Remarquer maxBins=41, nécessaire car la variable indexednativecountry possède 41 modalités (voir ici pour plus d’explications).
gbt = GBTClassifier(labelCol="indexedincome", featuresCol="indexedFeaturesAll", \
maxIter=100, maxBins=41)
pipeline = Pipeline(stages=[gbt])
fullGBTmodel = pipeline.fit(trainingDataFull)
predictionsFull = fullGBTmodel.transform(testDataFull)
evaluatorFull = MulticlassClassificationEvaluator( \
labelCol="indexedincome", \
predictionCol="prediction", \
metricName="accuracy")
accuracyFull = evaluatorFull.evaluate(predictionsFull)
print("Test accuracy with all features = %g" % (accuracyFull))
Modèle obtenu avec les seuls attributs ECOA-compatibles¶
Considérons maintenant un modèle développé avec les variables qui respectent la réglementation ECOA (Equal Credit Opportunity Act), donc sans age, maritalstatus, race, sex, nativecountry.
featureAssemblerECOA = VectorAssembler(inputCols = \
['indexedworkclass', 'fnlwgt', \
'indexededucation', 'educationnum', \
'indexedoccupation', \
'indexedrelationship', \
'capitalgain', 'capitalloss', \
'hoursperweek'], \
outputCol = 'indexedFeaturesECOA')
sparkDFassembledECOA = featureAssemblerECOA.transform(sparkDF)
sparkDFassembledECOA.printSchema()
(trainingDataECOA, testDataECOA) = sparkDFassembledECOA.randomSplit([0.7, 0.3], 100)
gbt = GBTClassifier(labelCol="indexedincome", featuresCol="indexedFeaturesECOA", \
maxIter=100, maxBins=41)
pipeline = Pipeline(stages=[gbt])
ecoaGBTmodel = pipeline.fit(trainingDataECOA)
predictionsECOA = ecoaGBTmodel.transform(testDataECOA)
evaluatorECOA = MulticlassClassificationEvaluator( \
labelCol="indexedincome", \
predictionCol="prediction", \
metricName="accuracy")
accuracyECOA = evaluatorECOA.evaluate(predictionsECOA)
print("Test accuracy with ECOA-complying features = %g" % (accuracyECOA))
On constate sur les données de test une performance (accuracy, ou taux de bons classements) proche de celle du modèle mis au point avec toutes les variables.
Analyse des disparités¶
Examinons maintenant les disparités présentes dans les prédictions des deux modèles. Nous nous intéressons à deux critères observationnels :
Le critère d’indépendance (demographic parity) : la prédiction \(\hat{Y}\) est-elle indépendante de l’attribut protégé \(A\) ? Autrement dit, le taux de prédits positifs est-il le même pour les différentes valeurs de l’attribut protégé ?
Le critère de séparation (equalized odds) : la prédiction \(\hat{Y}\) est-elle indépendante de l’attribut protégé \(A\) conditionnellement à la variable cible \(Y\) ? Autrement dit, y a-t-il le même taux de vrais positifs \(P(\hat{Y}=1|Y=1,A=a) = P(\hat{Y}=1|Y=1,A=b)\) et le même taux de faux positifs \(P(\hat{Y}=1|Y=0,A=a) = P(\hat{Y}=1|Y=0,A=b)\) pour les différentes valeurs de l’attribut protégé ?
Critère d’indépendance¶
Examinons d’abord le critère d’indépendance (ou de parité démographique) à travers le taux de parité démographique, c’est à dire le rapport entre les taux de prédits positifs pour les différentes valeurs de l’attribut protégé. Si la parité était respectée, ce taux devrait être égal à 1.
print("Disparités présentes dans les données de test (indépendance entre A et Y) ?")
predictionsFull.groupBy("sex").avg("indexedincome").show()
print("Parité démographique du prédicteur (indépendence entre A et Ŷ) ?")
print("modèle qui emploie toutes les variables, y compris attributs protégés :")
predictionsFull.groupBy("sex").avg("prediction").show()
pF = predictionsFull.groupBy("sex").avg("prediction").toPandas()
print("taux de parité démographique avec toutes les variables : ", \
pF['avg(prediction)'][0]/pF['avg(prediction)'][1])
print("modèle qui emploie les variables conformes ECOA :")
predictionsECOA.groupBy("sex").avg("prediction").show()
pE = predictionsECOA.groupBy("sex").avg("prediction").toPandas()
print("taux de parité démographique avec variables ECOA : ", \
pE['avg(prediction)'][0]/pE['avg(prediction)'][1])
Aucun des deux modèles ne respecte la parité démographique, et le taux de parité démographique n’est pas amélioré ici par l’exclusion des attributs protégés.
Critère de séparation¶
Pour le critère equalized odds (séparation) nous devons calculer les taux de faux positifs et les taux de vrais positifs pour chacune des modalités d’un attribut protégé. L’analyse qui suit considère l’attribut protégé sex.
Pour le modèle qui emploie toutes les variables (y compris les attributs protégés) nous obtenons :
predictionAndLabelsM = predictionsFull.filter(predictionsFull.sex=='Male').select('prediction','indexedincome')
predictionAndLabelsMnegs = predictionAndLabelsM.filter(predictionAndLabelsM.indexedincome==0.0)
predictionAndLabelsMpos = predictionAndLabelsM.filter(predictionAndLabelsM.indexedincome==1.0)
fprM = predictionAndLabelsMnegs.filter(predictionAndLabelsMnegs.prediction==1.0).count() \
/ predictionAndLabelsMnegs.count()
tprM = predictionAndLabelsMpos.filter(predictionAndLabelsMpos.prediction==1.0).count() \
/ predictionAndLabelsMpos.count()
print("Taux de faux positifs pour Male = ", fprM)
print("Taux de vrais positifs pour Male = ", tprM)
predictionAndLabelsF = predictionsFull.filter(predictionsFull.sex=='Female').select('prediction','indexedincome')
predictionAndLabelsFnegs = predictionAndLabelsF.filter(predictionAndLabelsF.indexedincome==0.0)
predictionAndLabelsFpos = predictionAndLabelsF.filter(predictionAndLabelsF.indexedincome==1.0)
fprF = predictionAndLabelsFnegs.filter(predictionAndLabelsFnegs.prediction==1.0).count() \
/ predictionAndLabelsFnegs.count()
tprF = predictionAndLabelsFpos.filter(predictionAndLabelsFpos.prediction==1.0).count() \
/ predictionAndLabelsFpos.count()
print("Taux de faux positifs pour Female = ", fprF)
print("Taux de vrais positifs pour Female = ", tprF)
On constate que les taux de vrais positifs \(P(\hat{Y}=1|Y=1,A=a)\), \(P(\hat{Y}=1|Y=1,A=b)\) sont différents pour les différentes valeurs de l’attribut protégé sex, ainsi que les taux de faux positifs \(P(\hat{Y}=1|Y=0,A=a)\), \(P(\hat{Y}=1|Y=0,A=b)\). Le critère equalized odds (séparation) n’est donc pas respecté.
Nous pouvons aussi illustrer sur le repère habituel des courbes ROC (en abscisse le taux de faux positifs, en ordonnée le taux de vrais positifs) où se situe le modèle pour chaque modalité de l’attribut protégé sex :
import matplotlib.pyplot as plt
plt.title('Modèle qui emploie toutes les variables')
plt.xlabel('Taux de faux positifs')
plt.ylabel('Taux de vrais positifs')
plt.scatter(fprM, tprM, label='Male')
plt.scatter(fprF, tprF, label='Female')
#plt.plot([0.0, fprM, 1.0],[0.0, tprM, 1.0], label='Male')
#plt.plot([0.0, fprF, 1.0],[0.0, tprF, 1.0], label='Female')
plt.plot([0.0, 1.0],[0.0, 1.0], 'k--')
plt.legend()
Le résultat devrait ressembler à :
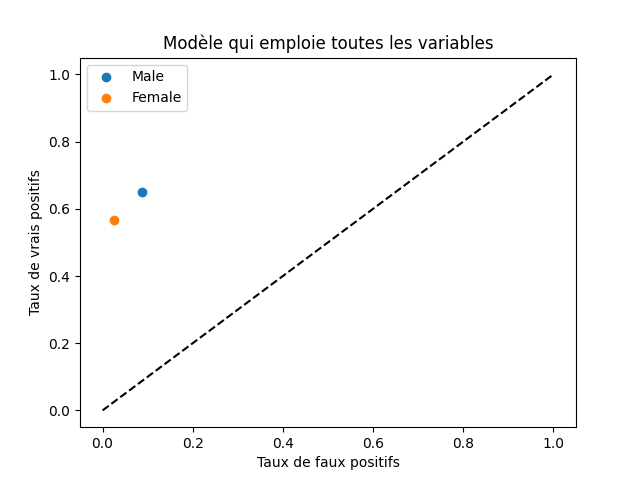
Fig. 136 Courbes ROC pour le modèle qui emploie toutes les variables¶
Pour le modèle qui emploie seulement les variables conformes à ECOA (donc sans les attributs protégés) nous obtenons :
predictionAndLabelsM = predictionsECOA.filter(predictionsECOA.sex=='Male').select('prediction','indexedincome')
predictionAndLabelsMnegs = predictionAndLabelsM.filter(predictionAndLabelsM.indexedincome==0.0)
nM = predictionAndLabelsMnegs.count()
fpM_0 = predictionAndLabelsMnegs.filter(predictionAndLabelsMnegs.prediction==1.0).count()
predictionAndLabelsMpos = predictionAndLabelsM.filter(predictionAndLabelsM.indexedincome==1.0)
pM = predictionAndLabelsMpos.count()
tpM_0 = predictionAndLabelsMpos.filter(predictionAndLabelsMpos.prediction==1.0).count()
fprM_0 = fpM_0 / nM
tprM_0 = tpM_0 / pM
print("Taux de faux positifs pour Male = ", fprM_0)
print("Taux de vrais positifs pour Male = ", tprM_0)
predictionAndLabelsF = predictionsECOA.filter(predictionsECOA.sex=='Female').select('prediction','indexedincome')
predictionAndLabelsFnegs = predictionAndLabelsF.filter(predictionAndLabelsF.indexedincome==0.0)
nF = predictionAndLabelsFnegs.count()
fpF_0 = predictionAndLabelsFnegs.filter(predictionAndLabelsFnegs.prediction==1.0).count()
predictionAndLabelsFpos = predictionAndLabelsF.filter(predictionAndLabelsF.indexedincome==1.0)
pF = predictionAndLabelsFpos.count()
tpF_0 = predictionAndLabelsFpos.filter(predictionAndLabelsFpos.prediction==1.0).count()
fprF_0 = fpF_0 / nF
tprF_0 = tpF_0 / pF
print("Taux de faux positifs pour Female = ", fprF_0)
print("Taux de vrais positifs pour Female = ", tprF_0)
On constate que, pour le modèle qui n’emploie pas les attributs protégés, les taux de vrais positifs \(P(\hat{Y}=1|Y=1,A=a)\), \(P(\hat{Y}=1|Y=1,A=b)\) sont différents pour les différentes valeurs de l’attribut protégé sex, ainsi que les taux de faux positifs \(P(\hat{Y}=1|Y=0,A=a)\), \(P(\hat{Y}=1|Y=0,A=b)\). Donc ce modèle ne respecte pas, lui non plus, le critère equalized odds (séparation).
Nous pouvons également illustrer sur le repère habituel des courbes ROC (en abscisse le taux de faux positifs, en ordonnée le taux de vrais positifs) où se situe ce modèle pour chaque modalité de l’attribut protégé sex :
import matplotlib.pyplot as plt
plt.title('Modèle qui emploie les variables ECOA')
plt.xlabel('Taux de faux positifs')
plt.ylabel('Taux de vrais positifs')
plt.scatter(fprM_0, tprM_0, label='Male')
plt.scatter(fprF_0, tprF_0, label='Female')
#plt.plot([0.0, fprM_0, 1.0],[0.0, tprM_0, 1.0], label='Male')
#plt.plot([0.0, fprF_0, 1.0],[0.0, tprF_0, 1.0], label='Female')
plt.plot([0.0, 1.0],[0.0, 1.0], 'k--')
plt.legend()
Le résultat devrait ressembler à :
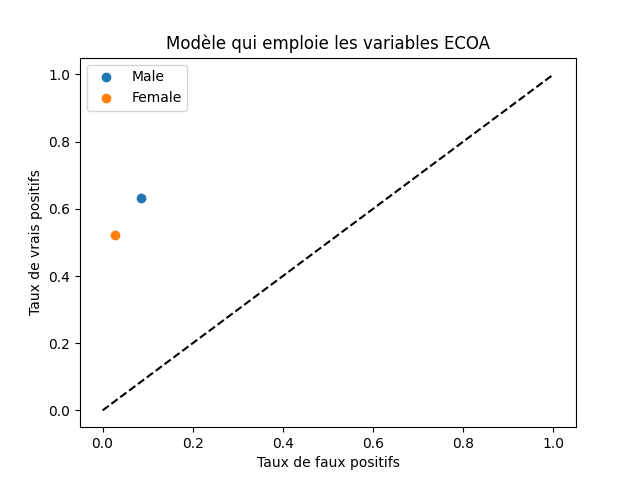
Fig. 137 Courbes ROC pour le modèle qui emploie les variables ECOA¶
On constate que ni le modèle mis au point avec toutes les variables, ni celui développé avec les seules variables conformes à ECOA, ne respectent le critère equalized odds.
Pouvons-nous prédire des attributs protégés à partir des autres ?¶
Nous avons constaté que ce n’est pas parce que les attributs protégés (ECOA dans le cas présent) sont éliminés de la modélisation que le modèle respecte nécessairement des critères observationnels de non discrimination. Une des explications possibles est que les attributs restants permettent de prédire les attributs protégés manquants, même en l’absence de véritables variables proxy pour ces attributs.
Examinons maintenant dans quelle mesure il est possible de prédire la valeur de l’attribut protégé race à partir des attributs qui ne sont pas protégés. Dans Spark, la méthode Gradient Boosted Trees (GBT) est implémentée seulement pour la classification binaire, nous nous servirons donc d’une forêt aléatoire (random forest) à la place de GBT en classification multi-classe :
from pyspark.ml.classification import RandomForestClassifier
featureAssemblerRPred = VectorAssembler(inputCols = \
['indexedworkclass', 'fnlwgt', \
'indexededucation', 'educationnum', \
'indexedoccupation', \
'indexedrelationship', \
'capitalgain', 'capitalloss', \
'hoursperweek'], \
outputCol = 'indexedFeaturesRPred')
sparkDFassembledRPred = featureAssemblerRPred.transform(sparkDF)
sparkDFassembledRPred.printSchema()
(trainingDataRPred, testDataRPred) = sparkDFassembledRPred.randomSplit([0.7, 0.3], 100)
rfc = RandomForestClassifier(labelCol="indexedrace", featuresCol="indexedFeaturesRPred", \
numTrees=100, maxBins=41)
pipeline = Pipeline(stages=[rfc])
rPredRFmodel = pipeline.fit(trainingDataRPred)
predictionsRPred = rPredRFmodel.transform(testDataRPred)
evaluatorRPred = MulticlassClassificationEvaluator( \
labelCol="indexedincome", \
predictionCol="prediction", \
metricName="accuracy")
accuracyRPred = evaluatorRPred.evaluate(predictionsRPred)
print("Test accuracy for predicting 'race' from the ECOA features = %g" % (accuracyRPred))
Question :
Comment interpréter ces résultats ?
Correction :
L’attribut protégé race possède 5 modalités, une accuracy de 0.76 sur les données de test pour ce problème de prédiction à 5 classes est donc relativement élevée.
Question :
Dans quelle mesure pouvons-nous prédire la valeur de l’attribut protégé sex à partir des attributs conformes ECOA (Equal Credit Opportunity Act) ?
Correction :
L’attribut sex étant binaire, il est possible de revenir à GBT ou de continuer avec random forest. Le code ressemble fortement à celui pour la prédiction de race.
Réduction ou suppréssion des disparités dans un modèle¶
Nous présentons maintenant une méthode de post-traitement qui permet d’obtenir un modèle qui respecte le critère de séparation (equalized odds) à partir d’un modèle initial qui, lui, ne respecte pas ce critère. La méthode a été proposée dans [HPS16] et cherche à optimiser la performance (accuracy) du modèle dérivé. Nous avons choisi d’exposer cette méthode car elle est générale, pouvant s’appliquer à un modèle qui fait des prédictions binaires (où nous n’avons pas accès à un score quantitatif), sans exiger l’accès aux données d’apprentissage ou à la procédure d’apprentissage.
Le principe de la méthode est le suivant :
Pour le modèle initial, les taux de faux positifs et de vrais positifs sont différents pour les différentes modalités de l’attribut protégé (c’est en cela que le critère de séparation ou equalized odds n’est pas respecté). Pour corriger le modèle afin de satisfaire à ce critère, il est nécessaire d’augmenter le taux de prédictions positives (et ainsi à la fois le taux de vrais positifs et le taux de faux positifs) lorsque l’attribut protégé prend la valeur « défavorisée » et/ou de réduire le taux de prédictions positives lorsque l’attribut protégé prend la valeur « favorisée ». Si le modèle initial disponible prédit directement une variable nominale \(\hat{Y}\) (sans passer par un score intermédiaire \(R\)), une façon de faire ces modifications est d’utiliser une procédure de randomization : pour les « défavorisés » on convertit aléatoirement une partie des prédictions négatives en prédictions positives, pour les « favorisés » on convertit aléatoirement une partie des prédictions positives en prédictions négatives.
L’objectif est de déterminer les corrections à faire (de calculer les taux de conversion de prédictions) afin de respecter le critère equalized odds tout en maximisant la performance (accuracy) du modèle corrigé. Dans [HPS16] on démontre qu’un modèle corrigé respectant le critère equalized odds doit avoir sa réponse dans la région admissible qui est l’intersection entre les domaines situés entre la diagonale du diagramme ROC et les traits qui relient sur ce diagramme les réponses du modèle initial pour les « défavorisés » et respectivement les « favorisés » aux coins [0; 0] et [1; 1] de ce diagramme. Pour notre modèle initial à variables cornformes ECOA, ces domaines et leur intersection sont illustrés sur le figure suivante :
import matplotlib.pyplot as plt plt.title('Modèle qui emploie les variables ECOA') plt.xlabel('Taux de faux positifs') plt.ylabel('Taux de vrais positifs') plt.fill([0.0, fprM_0, 1.0],[0.0, tprM_0, 1.0], label='Male', color="r", alpha=0.2) plt.fill([0.0, fprF_0, 1.0],[0.0, tprF_0, 1.0], label='Female', color="b", alpha=0.2) plt.legend(loc='lower right')
Le résultat devrait ressembler à :
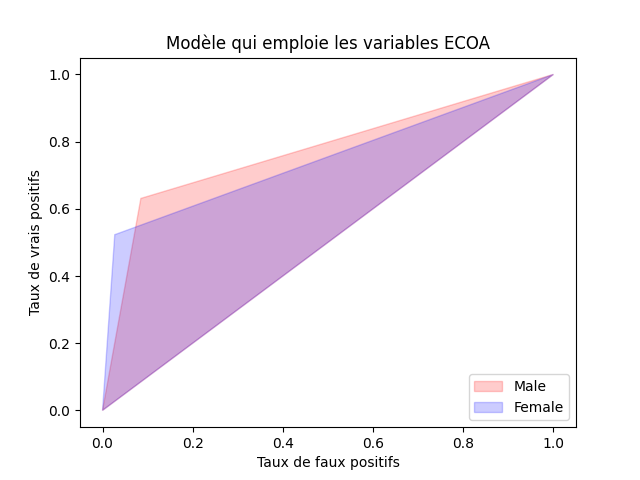
Fig. 138 Région admissible pour le modèle qui emploie les variables ECOA¶
Dans ce domaine, le point de performance (accuracy) maximale est le point du domaine admissible qui est le plus éloigné de la diagonale. Il peut être trouvé comme solution d’un problème d’optimisation linéaire. A partir des coordonnées de ce point et des taux de faux positifs et de vrais positifs du modèle initial pour chaque valeur de l’attribut protégé (les « défavorisés » et respectivement les « favorisés ») il est possible de calculer les taux de conversion de prédictions.
Lors de la prédiction, la décision du modèle initial est conservée ou modifiée en fonction de la valeur de l’attribut protégé et suivant le résultat d’un tirage aléatoire (randomization), en respectant les taux de changement de prédiction précalculés.
Il faut noter que la méthode proposée dans [HPS16] permet de traiter également le cas de modèles qui produisent plutôt un score \(R\) à partir duquel des prédictions \(\hat{Y}\) sont obtenues. Dans ce cas, employer des seuils différents pour les différentes valeurs de l’attribut protégé lorsqu’on transforme le score \(R\) en prédiction \(\hat{Y}\) peut suffire à obtenir un respect du critère de séparation (equalized odds). Une randomisation peut parfois être néanmoins nécessaire pour que le respect du critère soit strict.
Nous prenons comme modèle initial celui développé à partir des variales qui respectent ECOA et comme attribut protégé l’attribut binaire sex. Comme nous avons pu le constater plus haut, les taux de faux positifs et de vrais positifs sont différents pour les deux modalités de cet attribut.
L’objectif de la « correction » (proposée dans [HPS16]) du modèle initial est de le positionner dans le point le plus éloigné de la diagonale, au-dessus de la diagonale, dans la région admissible (même point pour les deux modalités de l’attribut protégé). Dans le cas général, trouver ce point optimal revient à faire appel à une méthode d’optimisation linéaire, en utilisant par exemple linprog de la bibliothèque Scipy, voir sa documentation. Cela implique de formuler précisément le problème d’optimisation :
dans le plan d’axes False Positive Ratio et True Positive Ratio nous cherchons le point solution \(\mathbf{x}\) de coordonnées [fpr, tpr] qui minimise une fonction (l’opposé de accuracy) en respectant des contraintes ;
la condition de minimisation est \(\min_{\mathbf{x}} \mathbf{c}^T \mathbf{x}\), avec ici \(\mathbf{c} = [1.0, -1.0]\), vecteur dirigé vers le coin bas à droite du diagramme ROC (taux de faux positifs = 1, taux de vrais positifs = 0) ; cette condition de minimisation indique que le point solution devrait être aussi « opposé » que possible au vecteur \(\mathbf{c}\) ;
les contraintes permettent de garder \(\mathbf{x}\) dans le domaine admissible ; chaque contrainte impose que le point solution soit du bon côté d’une des droites qui définissent le domaine (voir la figure qui montre le domaine admissible comme l’intersection de deux autres) : \(\mathbf{A}_{ub} \mathbf{x} \leq \mathbf{b}_{ub}\) ; ici, chaque ligne de \(\mathbf{A}_{ub}\) (et ligne correspondante de \(\mathbf{b}_{ub}\)) est obtenue en considérant le vecteur directeur d’une des droites, en le tournant de +90° (pour devenir orthogonal à la droite et orienté vers l’extérieur du domaine admissible) et en imposant la condition \(\leq s\), où \(s\) est le seuil correspondant (0 pour les trois droites qui passent par l’origine, à calculer pour les deux autres).
Plus précisément, les calculs à faire pour définir et résoudre le problème d’optimisation sont indiqués ci-dessous :
import numpy as np
c = np.array([1.0, -1.0]) # vecteur dirigé vers la accuracy minimale
#A = np.array([[-1.0, -1.0], \ # vecteur diagonale principale, orienté vers l'origine !
# [1.0-fprM_0, 1.0-tprM_0], \ # vecteur point M -> coin haut droite
# [1.0-fprF_0, 1.0-tprF_0], \ # vecteur point F -> coin haut droite
# [fprM_0, tprM_0], \ # vecteur origine -> point M
# [fprF_0, tprF_0]]) # vecteur origine -> point F
A = np.array([[-1.0, -1.0], \
[1.0-fprM_0, 1.0-tprM_0], \
[1.0-fprF_0, 1.0-tprF_0], \
[fprM_0, tprM_0], \
[fprF_0, tprF_0]])
Rm90 = np.array([[0.0, -1.0], [1.0, 0.0]]) # matrice de rotation +90°
A_ub = (Rm90.dot(A.transpose())).transpose()
penteM = (1.0-tprM_0) / (1.0-fprM_0)
penteF = (1.0-tprF_0) / (1.0-fprF_0)
b_ub = [0.0, 1-penteM, 1-penteF, 0.0, 0.0]
bounds = (0.0, 1.0) # les coordonnées varient entre 0 et 1
from scipy.optimize import linprog
res = linprog(c=c, A_ub=A_ub, b_ub=b_ub, bounds=bounds) # résolution programmation linéaire
print(res.x, res.fun, res.message) # res.x contient les coordonnées du point solution
fpr, tpr = res.x[0], res.x[1]
Dans notre cas précis, on peut voir sur le graphique obtenu par le code ci-dessous que le point recherché est le point d’intersection entre les droites [(0;0) (fprM;tprM)] et [(fprF;tprF) (1;1)] :
import matplotlib.pyplot as plt
plt.title('Modèle qui emploie les variables ECOA')
plt.xlabel('Taux de faux positifs')
plt.ylabel('Taux de vrais positifs')
plt.plot([0.0, fprM_0, 1.0],[0.0, tprM_0, 1.0], label='Male')
plt.plot([0.0, fprF_0, 1.0],[0.0, tprF_0, 1.0], label='Female')
plt.legend(loc='lower right')
Le résultat devrait ressembler à :

Fig. 139 Cible de correction pour le modèle qui emploie les variables ECOA¶
Nous pouvons nous servir alors plus simplement de la bibliothèque Shapely pour trouver ce point cible :
import shapely
from shapely.geometry import LineString, Point
ligne1 = LineString([Point(fprF_0,tprF_0), Point(1.0, 1.0)])
ligne2 = LineString([Point(0.0, 0.0), Point(fprM_0,tprM_0)])
#print(ligne1)
#print(ligne2)
intersection = ligne1.intersection(ligne2)
fpr = intersection.x # false positive rate cible (M et F)
tpr = intersection.y # true positive rate cible (M et F)
print("Cible pour le modèle : FPR =", fpr, ", TPR =", tpr)
Si la bibliothèque Shapely n’est pas disponible, nous pouvons écrire directement les équations des droites [(0;0) (fprM;tprM)] et [(fprF;tprF) (1;1)], pour ensuite trouver leur point d’intersection \((x, y)\) comme solution d’un système linéaire (seule la bibliothèque Numpy est nécessaire). Nous obtenons :
En conséquence, les calculs à faire pour trouver le point d’intersection sont :
import numpy as np
penteDiM = tprM_0 / fprM_0 # coefficient a
penteDiF = (1.0-tprF_0) / (1.0-fprF_0) # coefficient b
#lignes = np.array([[penteDiM, -1.0], \ # coef. droite (0.0, 0.0) -- (fprM_0,tprM_0)
# [penteDiF, -1.0]]) # coef. droite (fprF_0,tprF_0) -- (1.0, 1.0)
lignes = np.array([[penteDiM, -1.0], \
[penteDiF, -1.0]])
intersection = np.linalg.solve(lignes, np.array([0.0, penteDiF-1]))
fpr = intersection[0]
tpr = intersection[1]
print("Cible pour le modèle : FPR =", fpr, ", TPR =", tpr)
Une fois trouvé le point cible dans le diagramme ROC, pour obtenir le modèle cible (qui est le modèle initial dont une partie des prédictions sont modifiées) nous procédons par randomisation :
pour sex = M, on conserve \(\tilde{Y}=0\) mais on remplace aléatoirement une proportion \(propChangeM\) de \(\tilde{Y}=1\) par \(\tilde{Y}=0\) ;
pour sex = F, on conserve \(\tilde{Y}=1\) mais on remplace aléatoirement une proportion \(propChangeF\) de \(\tilde{Y}=0\) par \(\tilde{Y}=1\).
Le calcul des proportions de ppM (predicted positive Male) et de pnF (predicted negative Female) à changer pour espérer atteindre la cible fpr = intersection.x et tpr = intersection.y peut être fait de la façon suivante :
\(propChangeF = \frac{pnF_0 - pnF_1}{pnF_0}\), avec \(pnF_0 = F - (fpF_0 + tpF_0)\) et \(pnF_1 = F - (\frac{fpr \cdot fpF_0}{fprF_0} + \frac{tpr \cdot tpF_0}{tprF_0})\) ;
\(propChangeM = \frac{ppM_0 - ppM_1}{ppM_0}\), avec \(ppM_0 = fpM_0 + tpM_0\) et \(ppM_1 = \frac{fpr \cdot fpM_0}{fprM_0} + \frac{tpr \cdot tpM_0}{tprM_0}\).
Ces calculs sont mis en œuvre dans le programme suivant :
numFtestECOA = testDataECOA.filter(testDataECOA.sex=='Female').count()
pnF_0 = numFtestECOA - (fpF_0 + tpF_0)
pnF_1 = numFtestECOA - ((fpr * fpF_0) / fprF_0 + (tpr * tpF_0) / tprF_0)
propChangeF = (pnF_0 - pnF_1) / pnF_0
print("propChangeF: ", propChangeF)
ppM_0 = fpM_0 + tpM_0
ppM_1 = (fpr * fpM_0) / fprM_0 + (tpr * tpM_0) / tprM_0
propChangeM = (ppM_0 - ppM_1) / ppM_0
print("propChangeM: ", propChangeM)
Pour trouver le modèle corrigé, nous appliquons la randomisation au modèle GBT à variables ECOA (déjà obtenu plus haut), sur les données de test :
from pyspark.sql.functions import rand, when
# ajout d'une colonne qui doit accueillir les prédictions corigées
# ainsi que d'une colonne de valeurs aléatoires dans [0, 1) pour faire la randomisation
predictionsECOAadj = predictionsECOA.withColumn("correctedPrediction", predictionsECOA.prediction) \
.withColumn("random01", rand(seed=10))
# randomisation F : propChangeF des prédictions 0.0 sont remplacées par 1.0
# pour corriger la prédiction il faut avoir accès à l'attribut protégé !
predictionsECOAadj = predictionsECOAadj.withColumn("correctedPrediction", \
when((predictionsECOAadj.sex=='Female') & \
(predictionsECOAadj.prediction==0.0) & \
(predictionsECOAadj.random01 < propChangeF), 1.0) \
.otherwise(predictionsECOAadj.correctedPrediction))
# randomisation M : propChangeF des prédictions 1.0 sont remplacées par 0.0
# pour corriger la prédiction il faut avoir accès à l'attribut protégé !
predictionsECOAadj = predictionsECOAadj.withColumn("correctedPrediction", \
when((predictionsECOAadj.sex=='Male') & \
(predictionsECOAadj.prediction==1.0) & \
(predictionsECOAadj.random01 < propChangeM), 0.0) \
.otherwise(predictionsECOAadj.correctedPrediction))
#print(predictionsECOAadj.count()) # vérification
print(predictionsECOAadj.filter(predictionsECOAadj.prediction != \
predictionsECOAadj.correctedPrediction).count())
evaluatorECOAadj = MulticlassClassificationEvaluator( \
labelCol="indexedincome", \
predictionCol="correctedPrediction", \
metricName="accuracy")
accuracyECOAadj = evaluatorECOAadj.evaluate(predictionsECOAadj)
print("Accuracy avec variables ECOA avant ajustement = %g" % (accuracyECOA))
print("Accuracy avec variables ECOA après ajustement = %g" % (accuracyECOAadj))
La performance (accuracy) diminue suite à la correction par randomisation, mais dans notre exemple cette diminution est faible.
Il est maintenant possible de calculer les taux de faux et vrais positifs pour le modèle ECOA corrigé (c’est à dire à partir de la colonne correctedPrediction) :
predictionAndLabels = predictionsECOAadj.select('correctedPrediction','indexedincome')
predictionAndLabelsNegs = predictionAndLabels.filter(predictionAndLabels.indexedincome==0.0)
n = predictionAndLabelsNegs.count()
fp = predictionAndLabelsNegs.filter(predictionAndLabelsNegs.correctedPrediction==1.0).count()
predictionAndLabelsPos = predictionAndLabels.filter(predictionAndLabels.indexedincome==1.0)
p = predictionAndLabelsPos.count()
tp = predictionAndLabelsPos.filter(predictionAndLabelsPos.correctedPrediction==1.0).count()
fprAdj = fp / n
tprAdj = tp /p
predictionAndLabelsM = predictionsECOAadj.filter(predictionsECOA.sex=='Male') \
.select('correctedPrediction','indexedincome')
predictionAndLabelsMnegs = predictionAndLabelsM.filter(predictionAndLabelsM.indexedincome==0.0)
nM = predictionAndLabelsMnegs.count()
fpM = predictionAndLabelsMnegs.filter(predictionAndLabelsMnegs.correctedPrediction==1.0).count()
predictionAndLabelsMpos = predictionAndLabelsM.filter(predictionAndLabelsM.indexedincome==1.0)
pM = predictionAndLabelsMpos.count()
tpM = predictionAndLabelsMpos.filter(predictionAndLabelsMpos.correctedPrediction==1.0).count()
fprM = fpM / nM
tprM = tpM / pM
predictionAndLabelsF = predictionsECOAadj.filter(predictionsECOA.sex=='Female') \
.select('correctedPrediction','indexedincome')
predictionAndLabelsFnegs = predictionAndLabelsF.filter(predictionAndLabelsF.indexedincome==0.0)
nF = predictionAndLabelsFnegs.count()
fpF = predictionAndLabelsFnegs.filter(predictionAndLabelsFnegs.correctedPrediction==1.0).count()
predictionAndLabelsFpos = predictionAndLabelsF.filter(predictionAndLabelsF.indexedincome==1.0)
pF = predictionAndLabelsFpos.count()
tpF = predictionAndLabelsFpos.filter(predictionAndLabelsFpos.correctedPrediction==1.0).count()
fprF = fpF / nF
tprF = tpF / pF
print("Cible pour le modèle : TFP (False Positive Rate, FPR) =", fpr, ", TVP (True Positive Rate, TPR) =", tpr)
print("Résultat pour M : TFP (FPR) Male =", fprM, ", TVP (TPR) Male =", tprM)
print("Résultat pour F : TFP (FPR) Female =", fprF, ", TVP (TPR) Female =", tprF)
Naturellement, vu que les changements des prédictions sont appliqués aléatoirement et à des taux faibles, sur un échantillon limité (données de test ici) il ne faut pas s’attendre à des valeurs égales pour ces taux entre Male et Female.
Question :
Affichez un graphique permettant de vérifier visuellement si la correction appliquée a bien l’effet escompté.
Correction :
Une vérification visuelle, avec des lignes qui permettent de mieux vérifier la superposition que les points :
plt.title('Modèle corrigé qui respecte le critère de séparation')
plt.xlabel('Taux de faux positifs')
plt.ylabel('Taux de vrais positifs')
plt.plot([0.0, fprAdj, 1.0],[0.0, tprAdj, 1.0], label='Tous')
plt.plot([0.0, fprM, 1.0],[0.0, tprM, 1.0], label='Male')
plt.plot([0.0, fprF, 1.0],[0.0, tprF, 1.0], label='Female')
plt.plot([0.0, 1.0],[0.0, 1.0], 'k--')
plt.legend(loc='lower right')
Le résultat devrait ressembler à :
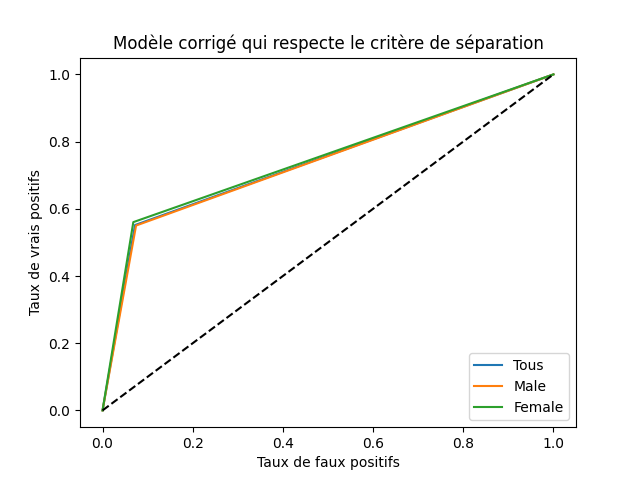
Fig. 140 Effet de la correction du modèle qui emploie les variables ECOA¶
Conclusion¶
Nous avons constaté, dans l’analyse et la modélisation des données Adult (issues de la collection de l’UCI) :
Les données Adult de départ contiennent des variables (ou attributs) protégées suivant la législation ECOA (Equal Credit Opportunity Act) :
age,maritalstatus,race,sex,nativecountry. Un modèle construit avec toutes ces variables ne respecterait donc pas cette réglementation.En supprimant ces variables protégées de la modélisation, les performances du modèle ne se dégradent pas de façon significative. Dans d’autres cas la dégradation des performances peut être plus forte lorsque les variables protégées (et leurs proxies) sont supprimées. Nous avions choisi comme méthode les Gradient Boosted Trees (GBT) afin de pouvoir mélanger variables quantitatives et nominales sans pré-traitement.
Les modèles obtenus ne respectent pas les critères observationnels d’équité, même en supprimant les variables protégées et en l’absence de variables proxy évidentes. La suppréssion des variables protégées et de leurs proxies ne suffit pas à garantir le respect de critères d’équité.
Un post-traitement permet de corriger un modèle pré-appris. Ici, la méthode de [HPS16] permet de changer les prédictions d’un modèle existant, pré-appris, pour que le modèle corrigé respecte le critère de séparation (equalized odds). Ici nous avons considéré le modèle développé sans accès aux attributs protégés, mais le modèle ayant appris avec tous les attributs (y compris les protégés) aurait pu être corrigé de façon similaire.
Pour corriger les prédictions il est indispensable d’avoir accès, lors de la prédiction, à l’attribut protégé pour lequel on souhaite appliquer la correction !

