Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.
Cours - Optimisation des réseaux de neurones artificiels¶
Pas d’apprentissage¶
Dans le chapitre précédent, nous avons vu que l’algorithme de rétropropagation permettait l’entraînement des réseaux de neurones multi-couches par une optimisation itérative à l’aide de la descente de gradient. Cette optimisatio nécessite de régler un hyperparamètre important : le pas d’apprentissage (ou taux d’apprentissage), le plus souvent noté \(\alpha\). En effet, le pas d’apprentissage contrôle l’amplitude des mises à jour durant la descente de gradient. Une valeur faible pour \(\alpha\) ralentit la convergence : il faudra plus d’itérations pour atteindre un minimum local. Néanmoins, choisir une valeur élevée pour \(\alpha\) peut provoquer des oscillations autour des minima locaux (phénomène dit d”overshoot), voire faire diverger l’optimisation et résulter en des instabilités numériques.
Le réglage du pas d’apprentissage se fait généralement par une recherche manuelle. En observant la convergence du modèle, il est possible de réduire ou d’augmenter le pas d’apprentissage et de répéter l’entraînement. Comme les réseaux de neurones profonds tendent à être coûteux en temps de calcul, il est préférable d’effectuer cette recherche sur un petit sous-ensemble du jeu de données. Le pas d’apprentissage idéal devrait permettre de sur-apprendre (overfit) sur le sous-ensemble avec le moins d’itérations possibles.
Néanmoins, un point à considérer est que le pas d’apprentissage idéal n’est pas constant lors de l’entraînement. En effet, lorsque la fonction de coût décroît lentement, il est préférable d’avoir un pas d’apprentissage plus élevé pour accélérer le déplacement dans l’espace des poids. Inversement, lorsque la fonction de coût décroît rapidement, il peut être intéressant de ralentir la mise à jour des paramètres pour éviter de dépasser un minimum. Nous verrons dans un chapitre ultérieur comment certaines variantes de l’algorithme de descente de gradient introduisent un pas d’apprentissage dit « adaptatif », qui s’ajuste automatiquement durant l’entraînement. Pour l’instant, nous pouvons nous concentrer sur les politiques d’évolution du pas d’apprentissage. En effet, il est courant de faire varier le pas d’apprentissage durant l’entraînement d’un modèle selon différentes stratégies.
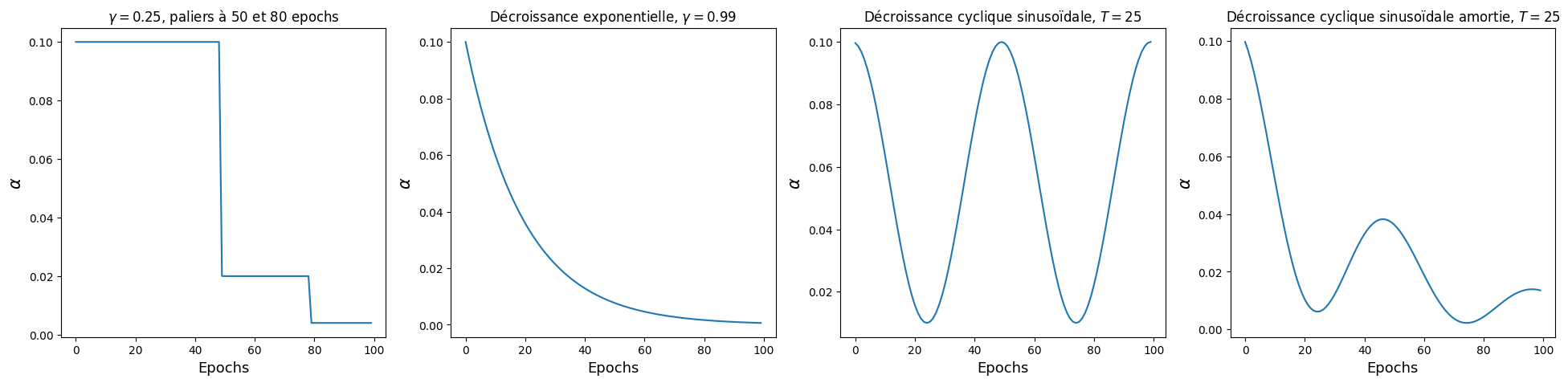
Fig. 85 Quelques exemples de politiques de mises à jour du pas d’apprentissage pendant l’optimisation. En général, les stratégies adoptées consistent à faire décroître lentement le taux d’apprentissage au fur et à mesure de l’entraînement. Néanmoins, il existe aussi des stratégies d’actualisation cycliques qui reviennent à des pas d’appprentissage élevés.¶
Dans l’ordre : décroissance par paliers, décroissance exponentielle, cosinus, cosinus amorti.
La stratégie la plus commune consiste à définir le pas d’apprentissage comme une fonction constante par morceaux, qui décroît d’un facteur \(0 < \gamma < 1\) après un certain nombre d’itérations. Par simplicité, nous allons définir les pas d’apprentissage en fonction du nombre d’epochs. Une epoch correspond à une passe entière sur le jeu de données d’apprentissage, c’est-à-dire le nombre d’itérations nécessaires pour parcourir une fois l’ensemble du jeu d’entraînement. Le nombre exact d’itérations est égal à \(\lfloor \frac{N}{k} \rfloor\) et dépend à la fois du nombre \(N\) d’exemples d’apprentissage et de la taille de batch \(k\) utilisée lors de l’entraînement. L’avantage du raisonnement en epochs est ainsi de ne pas être spécifique à un jeu de données.
La décroissance par paliers consiste donc à se fixer une valeur de \(\gamma\) et un nombre d’epochs après lequel le pas d’apprentissage initial sera multiplié par \(\gamma\). Ce processus peut se répéter autant de fois que souhaité. Il est courant d’utiliser ce type de stratégie pour diviser le pas d’apprentissage après, par exemple, 50% de l’entraînement puis 80% de l’entraînement.
Une seconde stratégie consiste à démarrer le pas d’apprentissage à une valeur modérée, puis à suivre une fonction décroissante. Par exemple, la décroissance exponentielle actualise le pas d’apprentissage \(\alpha_t\) avec :
où \(\gamma\) est un réel entre 0 et 1.
Bien qu’elles soient moins courantes, il existe toutefois des politiques d’évolution du pas d’apprentissage qui sont cycliques, suivant par exemple une courbe sinusoïdale de période \(T\) :
Ces politiques peuvent se combiner entre elles. Par exemple, appliquer à la fois un pas cyclique sinusoïdal et une décroissance exponentielle donne une décroissance en cosinus amorti, comme illustré dans la Fig. 85.
Régularisation des réseaux profonds¶
Weight decay¶
La régularisation par weight decay est aussi appelée régularisation par facteur d’oubli ou par dégradation des poids. Il s’agit d’une pénalité qui s’applique sur les paramètres du réseau de neurones et qui vient pénaliser l’amplitudes des poids. Dans le cas le plus commun, cette régularisation utilise la norme euclidienne des matrices de poids. Il s’agit ainsi de remplacer la fonction de coût choisie \(\mathcal{L}\) par une variante régularisée :
Le facteur \(\lambda\) est un réel positif \(>0\) qui contrôle l’importance de la régularisation.
Le weight decay permet de contraindre les poids à être proches de zéro. Intuitivement, des poids élevés conduisent à des variations rapides des activations même lorsque les entrées fluctuent faiblement. Or, nous faisons généralement l’hypothèse que la fonction à modéliser varie « doucement » et présente peu d’irrégularités. Concrètement, réduire l’amplitude des poids va réduire la variance des sorties du modèle. En effet, avec la plupart des fonctions d’activation habituelles, être proche de zéro contraint les paramètres à rester autour du régime de linéarité. La régularisation par weight decay est similaire à la régularisation de Tikhonov utilisée pour la régression Ridge.
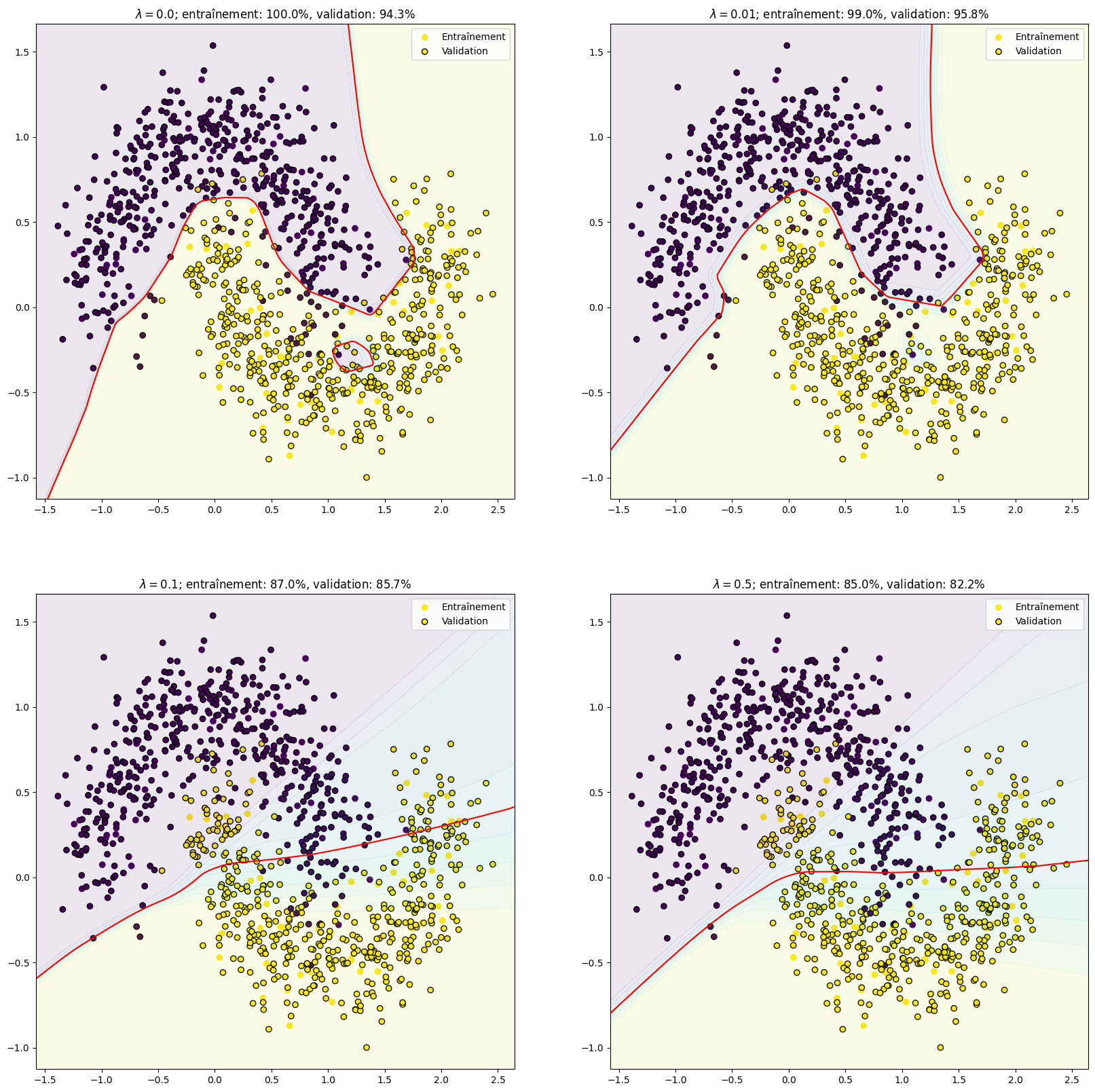
Illustration de l’influence du weight decay pour un perceptron à une couche cachée (2000 neurones) entraîné sur le problème de classification des deux lunes. Augmenter \(\lambda\) régularise le modèle et rend la frontière de décision plus régulière. Les performances en entraînement baissent légèrement, mais le score en validation augmente : le sur-apprentissage diminue. Toutefois, si la régularisation est trop forte, alors les performances diminuent à la fois en apprentissage et en validation : c’est le sous-apprentissage.¶
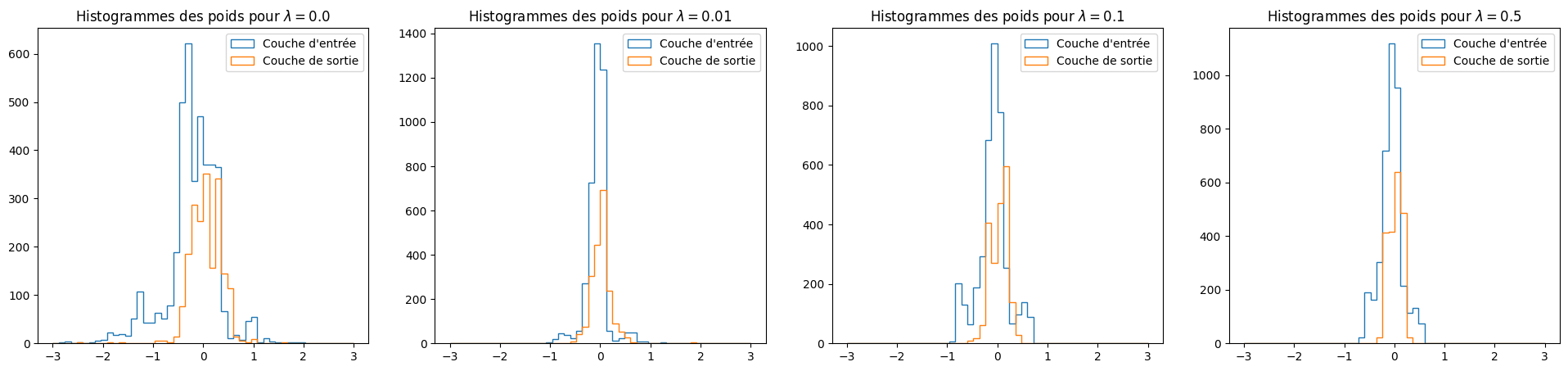
Illustration de l’impact du weight decay sur les paramètres du modèle. La distribution des poids, aussi bien pour la couche cachée que pour la couche de sortie, se resserre autour de zéro lorsque \(\lambda\) augmente. C’est le comportement attendu, puisque la régularisation par facteur d’oubli pénalise les poids de grande amplitude.¶
Le weight decay est présenté plus en détails dans cette séance de travaux pratiques de RCP208.
Dropout¶
Le Dropout [2SHK+14] est une opération régularisatrice consistant à mettre à zéro les activations en sortie d’une couche cachée avec une probabilité \(p\) lors de l’apprentissage. Ainsi, si \(p = \frac{1}{2}\), alors 50% des activations de la couche seront remplacées par des 0. Cette régularisation permet de limiter le sur-apprentissage en forçant l’information utile à être distribuée parmi toutes les activations. En effet, si toute l’information est concentrée sur une seule activation, si celle-ci est éliminée par Dropout alors le modèle ne sera pas en mesure de réaliser une prédiction correcte et l’erreur sera élevée.
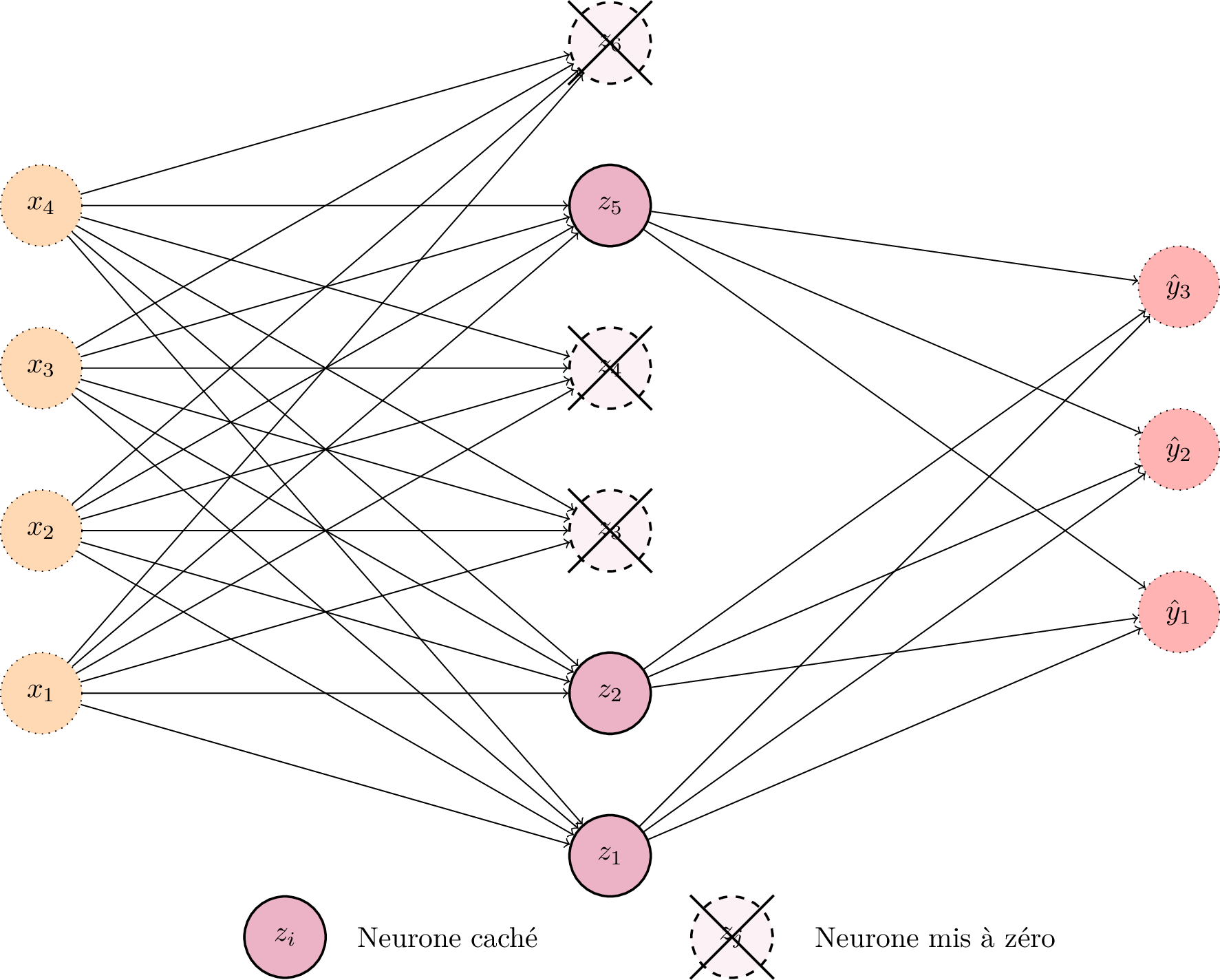
Pendant la phase d’entraînement, les neurones de la couche concernée par le Dropout sont aléatoirement mis à zéro avec une probabilité \(p\). Les activations étant nulles, les neurones concernés n’interviennent pas dans le calcul des activations de la couche suivante. Les neurones qui sont mis à zéro changent à chaque itération lors de l’entraînement.¶
Lors de la phase d’inférence, le Dropout est désactivé : il n’est pas souhaitable d’éliminer des activations aléatoirement, d’autant plus que cela rendrait la prédiction dépendant du hasard. Toutefois, on ne peut pas non plus appliquer les calculs en ignorant le Dropout car les poids ont été optimisés sur seulement une partie des activations. Pour conserver les amplitudes des activations, on les multiplie à l’inférence par \(1-p\).
Activations et initialisations¶
Fonctions d’activation¶
Saturation et gradients évanescents¶
Les fonctions d’activation non-linéaires classiques, comme la sigmoïde et la tangente hyperboliques, présente pour point commun d’exhiber deux régimes : un régime linéaire proche de zéro et un régime saturant pour les grandes activations.
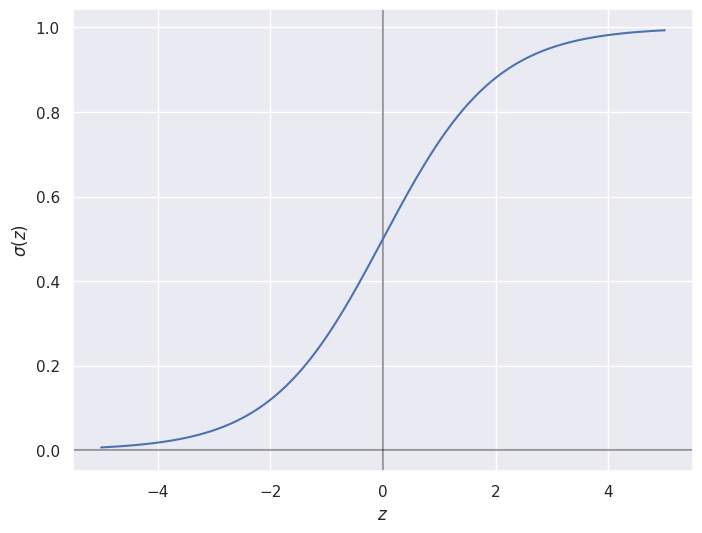
La fonction d’activation sigmoïde \(\sigma(z) = \frac{1}{1 + e^{-z}}\) prend ses valeurs dans le segment \([0,1]\). Elle tend vers 0 lorsque l’activation d’entrée tend vers \(-\infty\) et 1 vers \(+\infty\). Autour de 0, la sigmoide a un régime linéaire et sa courbe est quasi-confondue avec celle de la droite \(f(z) = z + \frac{1}{2}\).¶
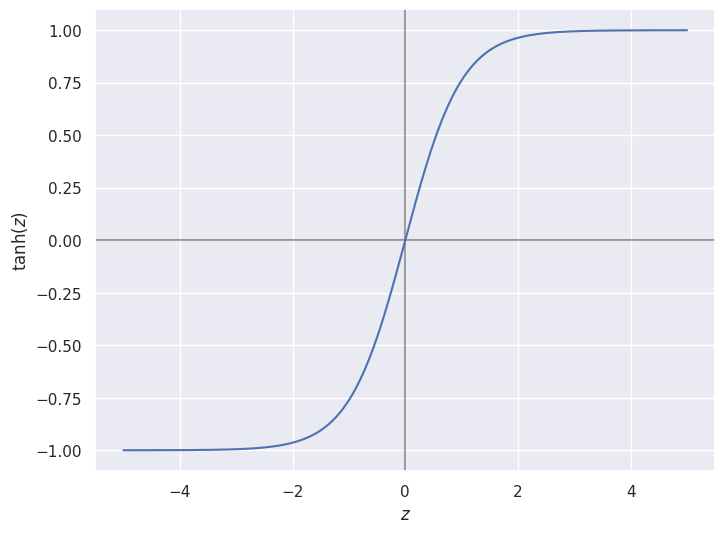
La fonction d’activation tangente hyperbolique \(\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\) prend ses valeurs dans le segment \([-1,+1]\). Elle tend vers -1 lorsque l’activation d’entrée tend vers \(-\infty\) et +1 vers \(+\infty\). Autour de 0, la tangente hyperbolique a un régime linéaire et sa courbe est quasi-confondue avec celle de la droite \(f(z) = z\).¶
Comme nous l’avons vu précédemment, la non-linéarité, et donc le régime de saturation, est ce qui transmet aux réseaux de neurones profonds leur expressivité. Si l’on remplace les activations par la fonction identité \(f(z) = z\), alors toutes les couches sont linéaires et le réseau est équivalent à un perceptron, aussi profond soit-il. Cependant, la présence des régimes de saturation n’est pas sans inconvénient. Considérons la rétropropagation du gradient pour une couche entièrement connectée de fonction d’activation \(\phi\). En notant l’entrée \(\mathbf{x}\), les poids \(\mathbf{W}\) et les biais \(\mathbf{b}\), la passe avant est donc :
Afin d’optimiser les couches précédentes, nous devons rétropropager le gradient de l’erreur à travers cette couche. Nous cherchons alors \(\frac{\partial \mathcal{L}}{\partial x_i} = \frac{\partial \mathcal{L}}{\partial y} \frac{\partial y}{\partial z} \frac{\partial z}{\partial x_i}\). Durant la rétropropagation, nous connaissons le gradient de l’erreur par rapport à la sortie, donc \(\frac{\partial \mathcal{L}}{\partial y}\) est connu. Nous avons déjà vu que \(\frac{\partial z_i}{\partial x_i} = \mathbf{W}^T\). Reste donc \(\frac{\partial y}{\partial z}\), qui se calcule simplement par rapport à la dérivée de la fonction d’activation \(\phi\), c’est-à-dire \(\frac{\partial y_i}{\partial z_i} = \phi'(z_i)\).
Or, dans les régimes de saturation, la dérivée de la fonction d’activation tend vers zéro ! Autrement dit, le gradient rétropropagé vers la couche précédente aura une norme plus faible que le gradient venant de la sortie. Ce phénomène est d’autant plus grave que, pour la sigmoide dont la dérivée est toujours inférieure à 1 (\(|\sigma'(z)| < 1\)), on peut garantir \(\frac{\partial \mathcal{L}}{\partial x} < \frac{\partial \mathcal{L}}{\partial y}\). Qui plus est, ce problème est renforcé par les réseaux profonds. En notant \(l\) l’indice de la profondeur de la couche, par récurrence on peut montrer que :
où \(\lambda\) est une constante telle que \(\lVert \phi' \rVert \leq \lambda\). Si \(\lambda < 1\), alors plus le réseau est profond, plus les gradients rétropropagés deviennent faibles : c’est le phénomène de gradients évanescents (vanishing gradients). Si \(\lambda > 1\), les gradients peuvent croître de manière incontrôlée : ce sont les gradients explosifs. En pratique, les gradients évanescents sont le problème le plus souvent rencontré dans les réseaux profonds. La présence des régimes de saturation induit généralement la disparition des gradients.
Note
Dérivées de la sigmoide et de la tangente hyperbolique
Une propriété remarquable de ces deux dérivées est qu’elles peuvent s’exprimer de façon simple à partir des valeurs de la fonction d’activation. Ainsi, durant la rétropropagation, la backward pass se calcule de façon efficace du moment que l’on a stocké les activations durant la forward pass.
Activation ReLU¶
Pour lutter contre ce phénomène, les réseaux de profonds modernes utilisent maintenant une fonction d’activation de la famille des activations linéaires rectifiées ou REctified Linear Unit (ReLU) [2NH10]. Ces fonctions d’activation sont simples à calculer :
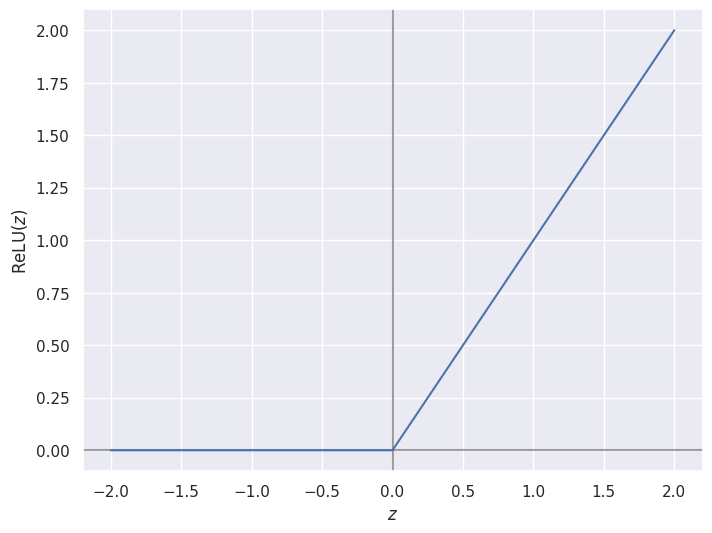
Fig. 91 Graphe de la fonction ReLU.¶
La fonction d’activation \(\operatorname{ReLU}(z) = \max(0, z)\) prend ses valeurs dans la demi-droite \([0,+\infty[\). Dans la partie positive, elle est égale à la fonction identité. Elle est constante et nulle dans sa partie négative.
La fonction d’activation ReLU (Fig. 91) a trois bénéfices principaux :
La décroissance de la norme du gradient est plus lente qu’avec la sigmoide ou la tangente hyperbolique, elle permet donc d’apprendre des réseaux de neurones plus profonds.
Les gradients étant de normes plus grandes car moins sujets à l’évanescence, la convergence du modèle par descente de gradient est plus rapide.
Son implémentation matérielle permet un calcul légèrement plus rapide des activations par rapport à la sigmoide qui fait intervenir une exponentielle.
Note
Dérivée de la fonction ReLU.
Remarquons que, dans le cas où l’activation ReLU est négative, le gradient rétropropagé pour le neurone concerné est nul. Dans certains cas, par exemple si le biais pour ce neurone est très fortement négatif, il est possible que l’activation ReLU devienne nulle pour toutes les entrées. C’est le phénomène de « ReLU mort ». Il est alors peu probable que l’entraînement permette de corriger ce phénomène, car le gradient rétropropagé est nul pour tous les exemples du jeu d’apprentissage.
Ce problème est corrigé par des variantes de la famille des fonctions linéaires rectifiées, telles que Leaky ReLU ou Exponential Linear Unit, donc le gradient est partout non-nul.
Initialisation des poids¶
Comme nous l’avons vu en introduisant la descente de gradient dans le cas multivarié, la descente de gradient stochastique dans le cas non-convexe ne permet que de déterminer des points stationnaires. Le point de départ de l’algorithme, l”initialisation, peut influer grandement sur l’optimum obtenu. Il est donc nécessaire de réfléchir à une initialisation des poids du réseau de neurones qui permette une convergence, idéalement vers un « bon » minimum.
Une idée naïve consisterait à initialiser tous les paramètres à la même valeur arbitraire (initialisation constante), par exemple zéro. Le problème de cette stratégie est que toutes les activations seront identiques et donc tous les neurones recevront le même gradient. Autrement dit, tous les poids évolueront de la même façon, ce qui restreint fortement les capacités de modélisation du réseau.
Une stratégie préférable consiste à utiliser une initialisation aléatoire. En reprenant les observations du weight decay, une bonne idée est d’initialiser les poids à une valeur faible pour se placer dans le régime linéaire et éviter le régime saturant (où le gradient rétropropagé est faible). Ainsi, initialiser les poids selon une distribution uniforme \(\mathcal{U}(-\sigma, +\sigma)\) ou normale \(\mathcal{N}(0, \sigma)\) de faible variance est généralement une bonne initialisation. Cependant, le choix de la variance n’est pas complètement triviale : pour que la fonction de transfert reste dans le régime linéaire, il faut donc que la somme des activations reçues soit inférieure à un certain seuil, qui dépend de la fonction d’activation et du nombre de neurones d’entrée.
Prenons pour exemple un perceptron multi-couche à 4 couches cachées de 500 neurones, d’entrée \(\mathbf{x}\) de dimension 10 et doté de la fonction d’activation \(\tanh\). On initialise les poids du modèle selon une loi normale \(\mathcal{N}(0, \sigma)\) et les biais à zéro. On passe ensuite une observation tirée aléatoirement selon une loi normale multivariée en entrée du modèle et l’on observe les histogrammes des activations à chaque couche cachée. Pour une variance faible (\(\sigma = 3.10^{-2}\)), on obtient les histogrammes suivants :
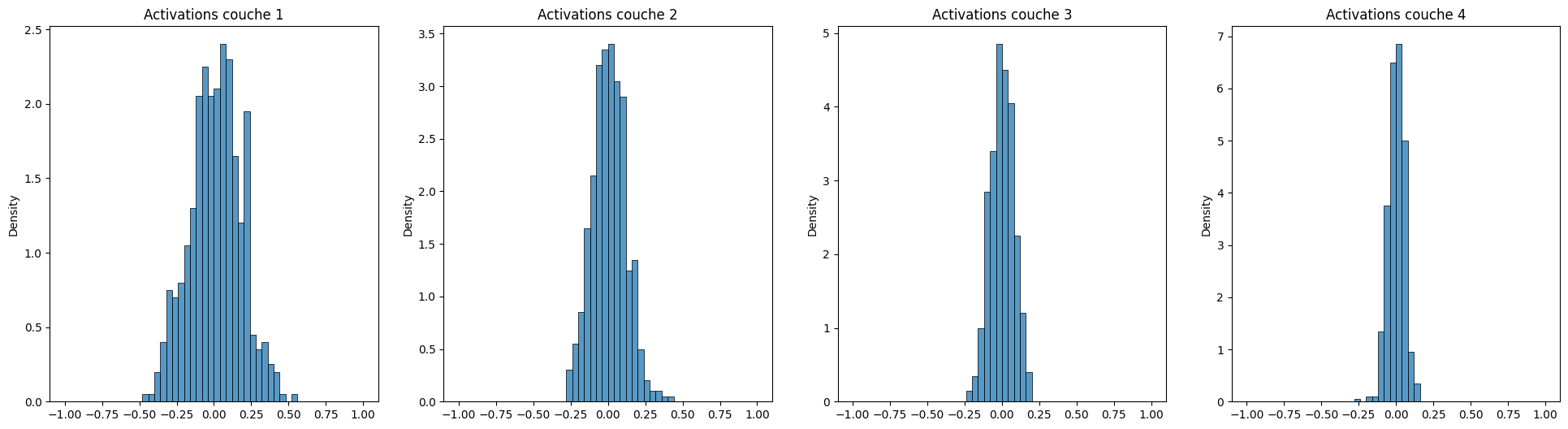
Histogrammes des activations pour les quatre couches cachées d’un perceptron multi-couche avec activation \(\tanh\), initialisé selon une loi normale de faible variance. La distribution se resserre autour de zéro au fil des couches.¶
Au fil des couches, les activations deviennent de plus en plus proches de zéro. Or, cela correspond également au régime linéaire de la tangente hyperbolique. Lors de l’initialisation, le perceptron multi-couche se comporte donc presque comme s’il n’y avait aucune non-linéarité, ce qui est l’inverse de ce que l’on espérait ! Inversement, si l’on choisit une variance plutôt élevée (\(\sigma = 1\)), on risque d’observer un autre phénomène, la saturation :
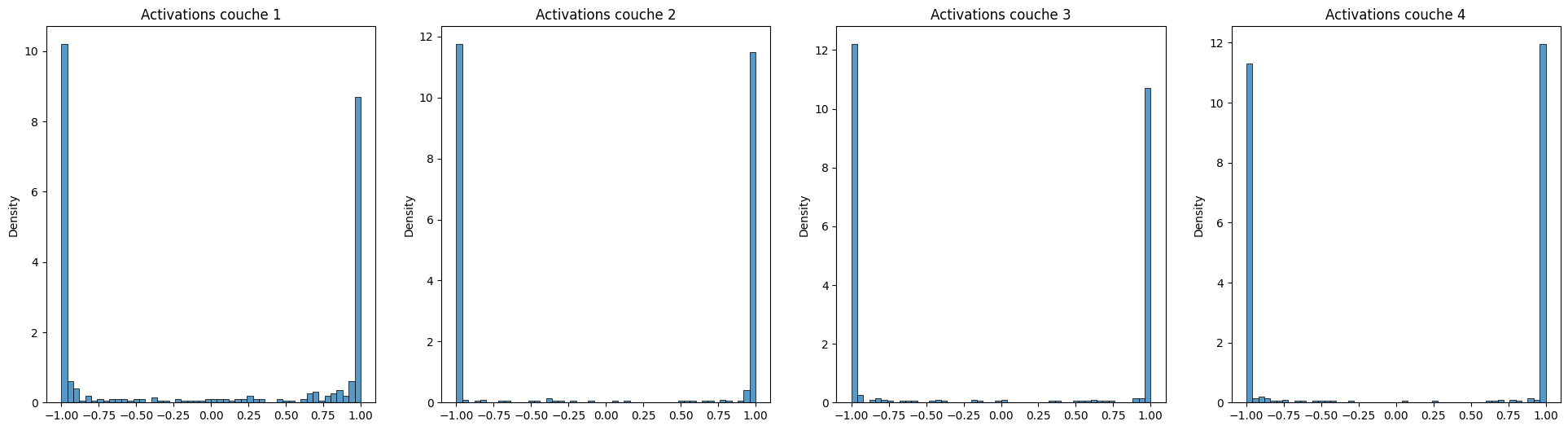
Histogrammes des activations pour les quatre couches cachées d’un perceptron multi-couche avec activation \(\tanh\), initialisé selon une loi normale de forte variance. La distribution est bimodale, avec des pics autour de -1 et de +1.¶
Comme les poids peuvent avoir des amplitudes élevées, les activations sont fortes et donc tombent immédiatement dans le régime de saturation (positif ou négatif) de la tangente hyperbolique : presque toutes les activations sont proches de +1 ou de -1. Si tous les neurones sont saturés, alors les gradients sont évanescents dès le départ. Ce n’est donc pas une bonne initialisation.
Les algorithmes d’initialisation de Glorot and Bengio et de He et al. permettent d’automatiser le choix de la variance dans le cas des réseaux à fonction d’activation tangente hyperbolique ou sigmoïde et ReLU, respectivement. Dans ce dernier cas, on peut montrer que si l’entrée \(\mathbf{x}\) est de dimension \(m\), alors la variance de la sortie \(s\) est égale à \(m \operatorname{Var}[\mathbf{w}] \operatorname{Var}[\mathbf{x}]\). Pour obtenir une sortie de variance unitaire, il suffit alors d’initialiser les poids en suivant la distribution \(\mathbf{w} \sim \frac{1}{\sqrt{m}} \mathcal{N}(0, \sigma)\).
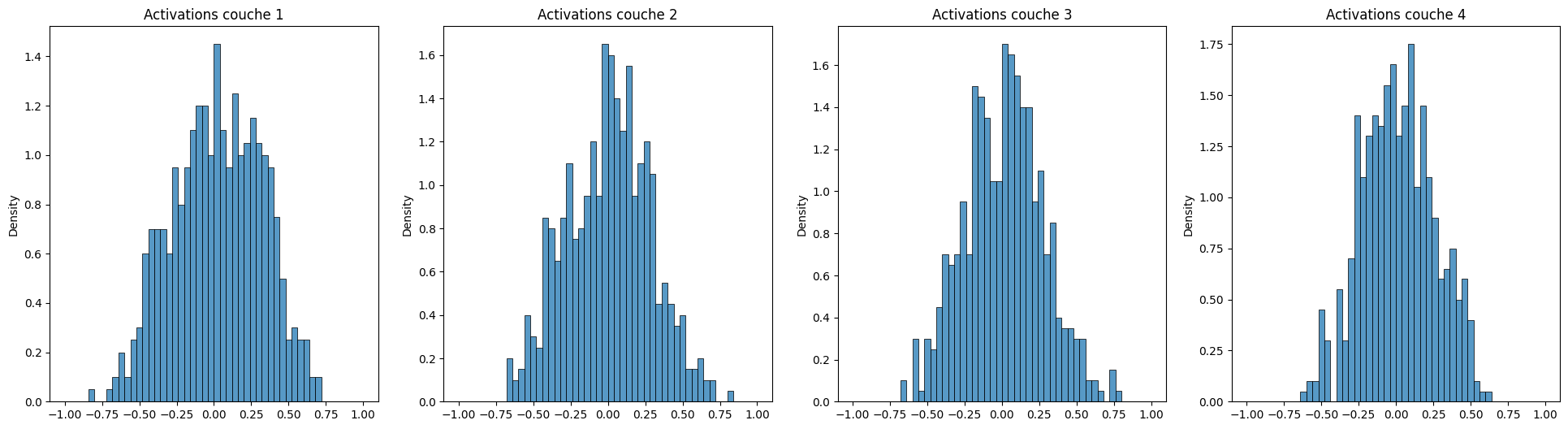
Histogrammes des activations pour les quatre couches cachées d’un perceptron multi-couche avec activation \(\tanh\), initialisé selon l’algorithme de Glorot. Les activations sont bien réparties quelque soit la couche considérée.¶
Note
Dans la grande majorité des cas, les biais sont initialisés à zéro. L’asymétrie est alors fournie par les poids. Dans le cas de l’activation ReLU, il est néanmoins courant d’utiliser un biais faible mais strictement positif (par exemple, \(10^{-2}\)) pour garantir que tous les neurones sont actifs à l’initialisation, et rétropropageront ainsi du gradient.
Xavier Glorot and Yoshua Bengio. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 249–256. March 2010.
Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision, 1026–1034. December 2015. doi:10.1109/ICCV.2015.123.
Vinod Nair and Geoffrey E. Hinton. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), 807–814. 2010.
Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. Journal of Machine Learning Research, 15:1929–1958, 2014.
