Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.

Cours - Réseaux de neurones récurrents

[Diapositives du cours]

Réseaux récurrents

Modélisation décisionnelle sur des séquences

Une séquence est une observation représentée par la \(\{\mathbf{x}_t\}\) pour \(t \in {1, T}\). Une valeur \(\mathbf{x}_t\) de la séquence au temps \(t\) peut être un scalaire (séquence univariée) ou un vecteur \(\mathbf{x}_t \in \mathbb{R}^d\) (séquence multivariée).

Considérons un jeu de données de séries temporelles \(\mathcal{D} = \{\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, \dots, \mathbf{x}^{(n)}\}\).

Toute la difficulté des problèmes de modélisation décisionnelle sur des séquences réside dans le fait que le nombre de variables explicatives dépend de la taille de l’historique considéré. Une option pour la modélisation décisionnelle consiste à décider que le contexte temporel d’intérêt est de longueur \(L\) fixe. Pour un problème de prévision, on prédit la valeur de \(x_{t+1}\) à partir des \(L\) valeurs précédentes : \(x_{t - L}, \dots, x_t\). Le nombre de variables explicatives est alors fixé, et la matrice d’observations complète correspond à toutes les fenêtres de taille \(L\) qu’il est possible d’extraire de l’ensemble des séries du jeu d’apprentissage \(\mathcal{D}\). Ce problème peut ensuite être traité par tous les modèles décisionnels vus jusqu’à présent : arbres de décision/forêts aléatoires, SVM, perceptrons multi-couche. Néanmoins, il y a trois inconvénients à cette approche :

1. Plus le contexte temporel nécessaire pour la modélisation est grand, plus le nombre de variables d’entrée augmente. Dans les perceptrons multi-couche, cela fait notamment accroître le nombre de paramètres du modèle.

2. Les prédictions \(y_t\) sont indépendantes pour chaque pas de temps \(x_t\) : le modèle ne prend pas en compte la prédiction qui a été effectuée au pas de temps précédent et n’a donc aucune « mémoire ».

3. Il est impossible de traiter des séquences de longueur inférieures à \(L\), et les séquences de longueur supérieures doivent être redécoupées et traitées fenêtre par fenêtre.

Cellule récurrente

Considérons une séquence d’entrée \(\{\mathbf{x}\}_{t \in \{1, T\}}\) de dimension \(d\), c’est-à-dire \(\mathbf{x_t} \in \mathbb{R}^d\). La cellule neuronale récurrente est définie par la séquence de ses états internes \(\{\mathbf{h}_t\}_{t \in \{1, T\}}\), de dimension \(l\), c’est-à-dire \(\mathbf{h}_t \in \mathbb{R}^l\). La séquence des états internes est définie par l’équation récurrente :

\[\mathbf{h}_t = \phi_t(\mathbf{x}_t, \mathbf{h}_{t-1})\]

Autrement dit, l’état interne \(\mathbf{h}_t\) au temps \(t\) dépend à la fois de la valeur de la séquence à ce même pas de temps et de son état interne au pas de temps précédent. L’état interne permet donc de modéliser l’historique de la séquence jusqu’au pas de temps \(t\) considéré.

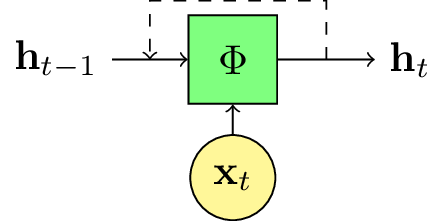
Fig. 111 Dans un réseau de neurone récurrent, l’état interne \(\mathbf{h}_t\) dépend à la fois de l’observation \(\mathbf{x}_t\) au pas de temps \(t\), mais aussi de l’état interne au pas de temps précédent. En général, la fonction de transfert \(\phi_t\) est identique pour tous les pas de temps.

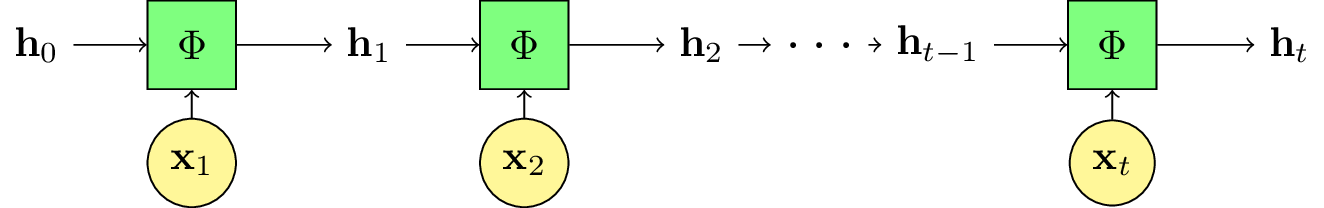
Fig. 112 La version « déroulée » du schéma précédent.

La question est maintenant de savoir comment choisir la fonction \(\phi_t\). Cette fonction est clé pour la boucle récursive puisqu’elle permet de passer d’un état interne au suivant, en lui adjoignant la nouvelle valeur de la séquence d’entrée \(\mathbf{x}_t\). Dans la formulation classique, cette fonction peut varier au cours du temps. Néanmoins, dans les réseaux de neurones récurrents, la fonction \(\phi_t\) sera identique pour tous les pas de temps \(t\). Nous la noterons donc simplement \(\phi\). En pratique, cela signifiera que les paramètres de la cellule récurrente sont partagés pour tous les pas de temps. Cela permettra d’avoir un unique jeu de paramètres, qui ne dépendra pas de la longueur des séquences à traiter.

Pour commencer simple, nous allons exiger que \(\phi\) appartienne à la famille des projections linéaires entre l’espace des entrées \(\mathbf{x}_t \in \mathbb{R}^d\) et l’espace des états internes \(\mathbf{h}_t \in \mathbb{R}^l\), suivies d’une fonction d’activation non-linéaire. Cela revient à utiliser la somme de deux couches entièrement connectées, dont nous connaissons maintenant bien l’équation :

\[\mathbf{h}_t = \phi\left(\underbrace{\mathbf{U}}_{\text{matrice}~ l\times d}\mathbf{x_t} + \underbrace{\mathbf{W}}_{\text{matrice}~ l\times l} \mathbf{h}_{t-1} + \underbrace{\mathbf{b}_h}_{\text{vecteur}~ l}\right)\]

où \(\phi : \mathbb{R} \rightarrow \mathbb{R}\) est une fonction d’activation non-linéaire, généralement \(\tanh\) ou une sigmoide.

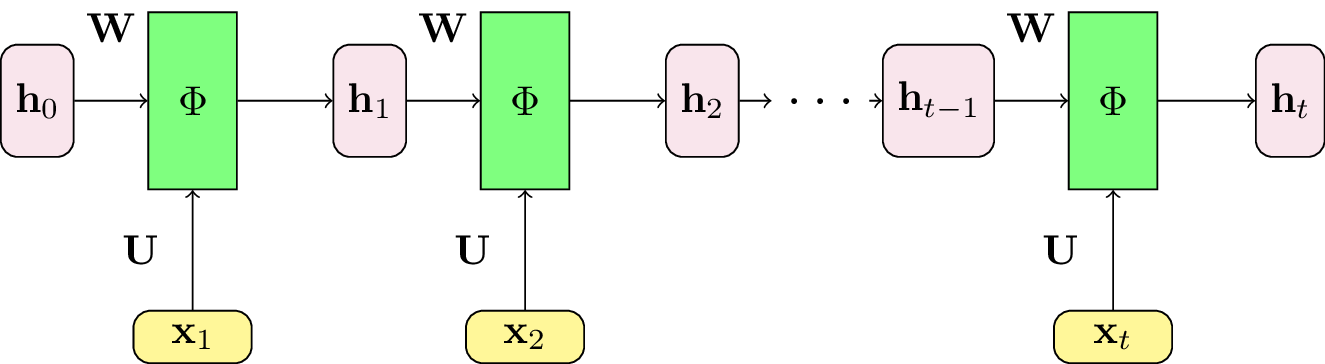
Fig. 113 Le réseau de neurones récurrent est construit à partir d’une cellule récurrente entièrement connectée. L’entrée \(\mathbf{x}_t\) et l’état interne précédent \(\mathbf{h}_{t-1}\) subissent une projection linéaire, puis l’application d’une fonction de transfert non-linéaire \(\Phi\). Les poids des perceptrons, c’est-à-dire les matrices \(U\) et \(W\), sont partagés pour tous les pas de temps.

Afin d’obtenir la sortie \(y_t\), il suffit d’appliquer à nouveau une couche entièrement connectée sur l’état interne de la cellule récurrente :

\[\mathbf{y}_t = \psi\left(\mathbf{V} \mathbf{h}_t + \mathbf{b}_y\right)\]

où \(\psi\) est soit l’identité, soit une fonction non-linéaire appliquée la sortie du modèle (par exemple, un softmax pour la classification).

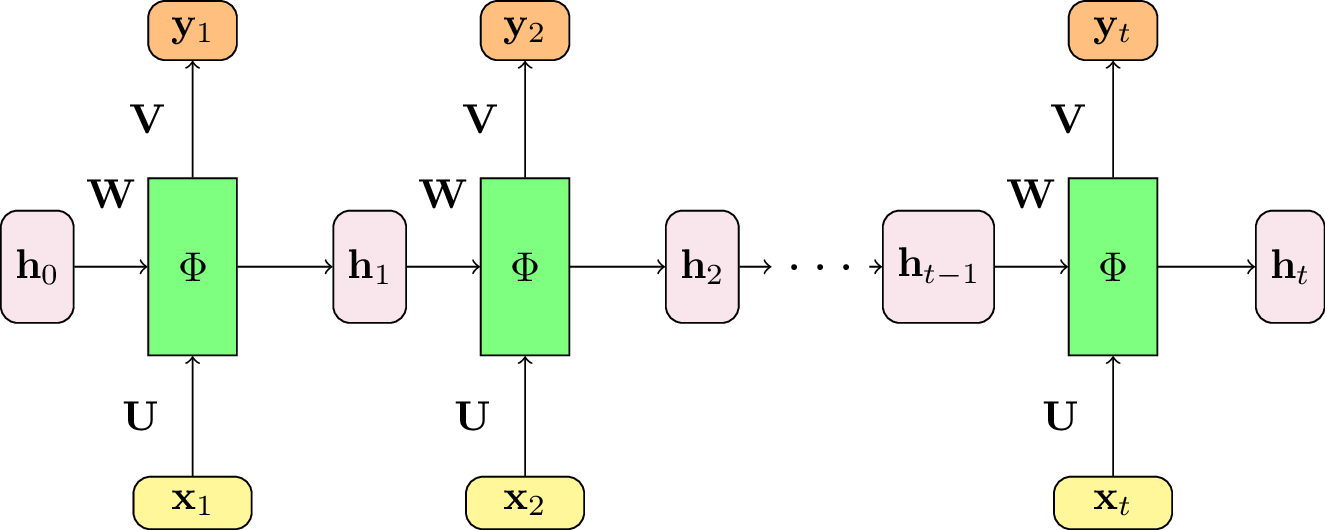
Fig. 114 Pour obtenir la sortie à chaque pas de temps, il suffit d’ajouter un perceptron passant de l’état interne \(\mathbf{h}_t\) à la variable de sortie \(y_t\). La matrice des poids \(\mathbf{V}\) est identique pour tous les pas de temps.

Rappelons que les matrices \(\mathbf{U}, \mathbf{V}\) et \(\mathbf{W}\), ainsi que les vecteurs de biais, ne dépendent pas du temps. Ainsi, le nombre de paramètres dans la cellule récurrente est seulement fonction de la dimension des entrées, la taille de l’état de l’interne et de la dimension des sorties.

Optimisation des réseaux récurrents

Comme dans le cas des réseaux de neurones classiques, les réseaux de neurones récurrents sont appris en minisant une fonction de coût \(\mathcal{L}\). La fonction de coût compare la sortie prédite \(\{\mathbf{y}_t\}_{t\in \{1;T\}}\) à la vérité terrain, c’est-à-dire l’information de supervision \(\{\mathbf{y}^*_t\}\). L’erreur totale pour une séquence correspond ainsi à la somme des erreurs pour tous les pas de temps :

\[\mathcal{L} = \sum_{t=1}^T \mathcal{L}_t(\mathbf{y}_t, \mathbf{y}^*_t; \theta)\]

qui dépend des paramètres \(\theta\) (\(\mathbf{W}, \mathbf{U}, \mathbf{V}\)) du réseau récurrent.

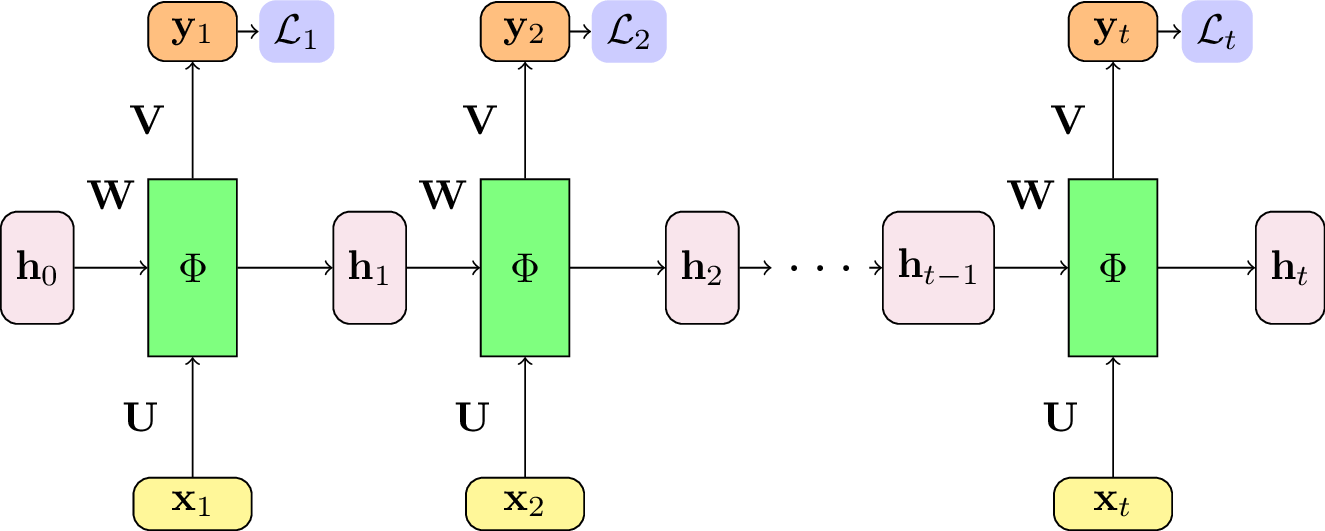
Fig. 115 La fonction de coût est calculée à chaque pas de temps. L’erreur totale correspond à la somme des erreurs sur une séquence.

Pour entraîner le modèle, nous pouvons donc appliquer l’algorithme de rétropropagation du gradient sur la version « déroulée » du réseau récurrent. Ce procédé correspond à l’algorithme de rétropropagation dans le temps ou backpropagation through time (BPTT). Une particularité des réseaux récurrents est que les paramètres \(\mathbf{W}, \mathbf{U}, \mathbf{V}\) sont partagés dans le temps. Les gradients dépendent donc de tout l’historique passé. Le raisonnement est identique pour tous les paramètres, donc nous ne considérerons que la matrice de poids \(\mathbf{W}\) pour illustrer la suite.

Afin d’optimiser le modèle par descente de gradient, il nous faut accéder au gradient de la fonction de coût par rapport aux paramètres \(\mathbf{W}\), c’est-à-dire \(\frac{\partial \mathcal{L}}{\partial \mathbf{W}}\). Or, nous avons défini l’erreur totale comme étant la somme des erreurs sur tous les pas de temps : \(\mathcal{L} = \sum_{t=1}^T \mathcal{L}_t\). Nous devons donc calculer \(\frac{\partial \mathcal{L}_t}{\partial \mathbf{W}}\).

En utilisant la chain rule, ce gradient peut se réécrire comme le produit des gradients de l’erreur par rapport à la sortie au pas de temps \(t\), du gradient entre la sortie et l’état interne, et de l’état interne par rapport à \(\mathbf{W}\) :

\[\frac{\partial \mathcal{L}_t}{\partial \mathbf{W}} = \frac{\partial \mathcal{L}_t}{\partial \mathbf{y}_t} \frac{\partial \mathbf{y}_t}{\mathbf{h}_t} \frac{\partial \mathbf{h}_t}{\partial \mathbf{W}}\]

\(\frac{\partial \mathcal{L}_t}{\partial \mathbf{y}_t}\) et \(\frac{\partial \mathbf{y}_t}{\mathbf{h}_t}\) ne posent pas de problème particulier, il s’agit du calcul classique de la rétropropagation des gradients dans un perceptron. Néanmoins, \(\frac{\partial \mathbf{h}_t}{\partial \mathbf{W}}\) est plus délicat à calculer, car \(\mathbf{h}_t\) dépend non seulement de \(\mathbf{W}\), mais aussi de \(\mathbf{h}_{t-1}\), qui dépend lui-même de \(\mathbf{W}\)! On obtient alors :

\[\frac{\partial \mathbf{h}_t}{\partial \mathbf{W}} = \frac{\partial \phi(\mathbf{x}_t, \mathbf{h}_{t-1}, \mathbf{W})}{\partial \mathbf{W}} + \frac{\partial \phi(\mathbf{x}_t, \mathbf{h}_{t-1}, \mathbf{W})}{\partial \mathbf{h}_{t-1}} \frac{\partial \mathbf{h}_{t-1}}{\partial \mathbf{W}}\]

Sans détailler la preuve, on peut montrer que :

\[\frac{\partial \mathbf{h}_t}{\partial \mathbf{W}} = \frac{\partial \phi(\mathbf{x}_t, \mathbf{h}_{t-1}, \mathbf{W})}{\partial \mathbf{W}} + \sum_{i=1}^{t-1} \left(\frac{\partial \phi(\mathbf{x}_j, \mathbf{h}_{j-1}, \mathbf{W})}{\partial \mathbf{h}_{j-1}}\right) \frac{\partial \phi(\mathbf{x}_i, \mathbf{h}_i, \mathbf{W}}{\partial \mathbf{W}}\]

Cette formulation a un inconvénient majeur : la chaîne des dérivées à calculer peut devenir très longue lorsque \(t\) est grand. Une solution est de se contenter d’une approximation du gradient en tronquant la somme après \(\Delta t\) étapes. Ainsi, on utilisera à la place la formule :

\[\frac{\partial \mathbf{h}_t}{\partial \mathbf{W}} = \frac{\partial \phi(\mathbf{x}_t, \mathbf{h}_{t-1}, \mathbf{W})}{\partial \mathbf{W}} + \sum_{i=\textcolor{red}{t - \Delta t}}^{t-1} \left(\frac{\partial \phi(\mathbf{x}_j, \mathbf{h}_{j-1}, \mathbf{W})}{\partial \mathbf{h}_{j-1}}\right) \frac{\partial \phi(\mathbf{x}_i, \mathbf{h}_i, \mathbf{W}}{\partial \mathbf{W}}\]

ce qui permet de limiter les calculs. Néanmoins, cela signifie également que la correction des erreurs ne se propagera pas plus loin que sur les \(\Delta t\) pas de temps précédents dans le passé. Autrement dit, le réseau de neurones récurrent ne pourra pas modéliser des phénomènes avec des dynamiques à long terme, si celles-ci ont lieu sur une temporalité supérieure au seuil de la BPTT tronquée.