Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.

Cours - Algorithmes à noyaux et applications

« Statistics is the grammar of science. »

(Karl Pearson)

[Diapositives du cours]

(cette page sera complétée avec les explications détaillées de la séance introductive du cours)

Objectifs et contenu de cette séance

Nous avons vu dans la séance précédente que « l’astuce à noyaux » permettait de non-linéariser tout algorithme linéaire qui utilise des produits scalaires. L’idée est de transposer les données dans un autre espace de dimension plus grande et ensuite appliquer l’algorithme linéaire sur les données projetées. Par la théorème de Mercer, si \(K\) est un noyau défini positif \(K: \mathbb{R}^d \times \mathbb{R}^d \rightarrow \mathbb{R}\) alors :

\[K(x,y) = \langle\phi(x), \phi(y)\rangle\]

où \(\phi:\mathbb{R}^d\rightarrow \mathcal{H}, x\rightarrow \phi(x)\) est une transformation de \(\mathbb{R}^d\) vers un espace de Hilbert \(\mathcal{H}\) qu’on n’as pas besoin d’expliciter : tout algorithme qui utilise seulement des produits scalaires entres les échantillons de données peut s’appliquer directement dans l’espace \(\mathcal{H}\) via le produit scalaire \(\langle\phi(x), \phi(y)\rangle = K(x,y)\).

Basés sur cet outil, dans cette séance nous présentons deux extensions de l’algorithme standard SVM : les SVM pour l’estimation du support d’une densité et les SVM pour la régression. Nous finissons par la présentation de quelques applications des SVM.

Estimation du support d’une densité

On considère les données d’apprentissage \(D = \{x_1, x_2, \dots, x_n\} \subset \mathcal{X}\), issues des variables i.i.d. suivant la densité de probabilité \(p(x)\) inconnue. Comme il ne s’agit pas d’un problème de classification, il n’y a pas d’étiquettes de classe \(y_i\). Le problème consiste à décider si une nouvelle observation \(x\) est proche ou non de cet ensemble \(D\), c’est-à-dire si elle est tirée de la même distribution. On cherche donc à estimer le support de cette densité : \(\{x|p(x)>0\}\). Il y a donc moins de difficultés que pour une estimation de densité : pour un point \(x\) il faut juste déterminer si \(p(x)>0\) et non prédire la valeur de \(p(x)\).

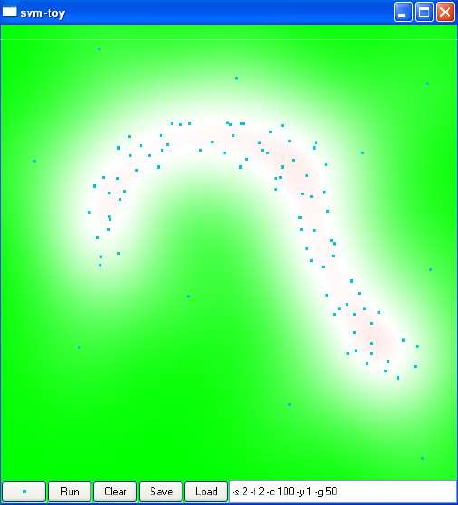
Fig. 63 Exemple issu de SVM-toy avec un noyau gaussien : il faut déterminer le support de la densité (région blanche). L’intensité de la couleur est proportionnelle à l’éloignement de la frontière.

Selon la modélisation géométrique du problème, on distingue deux approches pour le résoudre : SVDD (Support Vector Data Description) et OCSVM (One Class SVM).

Support Vector Data Description (SVDD)

Dans cette approche proposée dans [TD04] on cherche dans l’espace d’arrivée \(\mathcal{H}\) l’hypersphère la plus petite qui englobe les données :

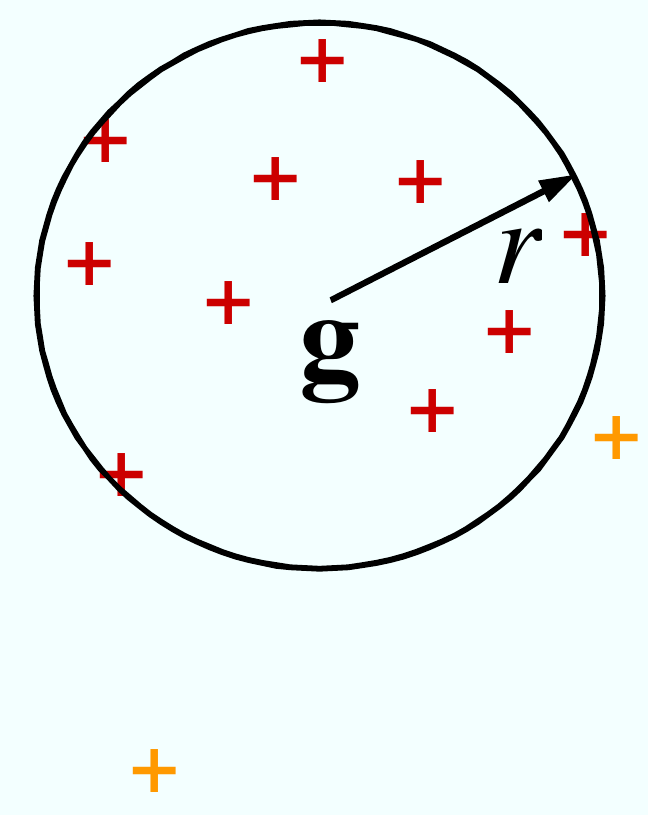
Fig. 64 SVDD cherche la sphère englobante minimale. La pré-image de l’intérieur de la sphère (dans l’espace de départ) donne le support de la densité.

Cette formulation conduit au problème d’optimisation suivant (voir [TD04]) :

\[\begin{split}\left\{ \begin{array}{lll} \underset{R,g}{\min}\; R^2 + C \sum_{i=1}^n\xi_i\\ \textrm{avec :}\\ ||x_i-g||^2 \leq R^2 + \xi_i, i = 1, \dots, n\\ \xi_i \geq 0, i = 1, \dots, n \end{array} \right.\end{split}\]

où \(g\) est le centre, \(R\) est le rayon et la constante \(C = \frac{1}{\nu n}\) permet de régler la proportion \(\nu\) de points que l’on désire maintenir en dehors de la boule (outliers).

Le problème dual est :

\[\begin{split}\left\{ \begin{array}{lll} \underset{\alpha}{\min}\; \frac{1}{2}\alpha^T K \alpha - \frac{1}{2} \alpha^T \textrm{diag}(K)\\ \textrm{avec} :\\ e^t \alpha = 1\\ 0 \leq \alpha_i <= C, i = 1, \dots, n \end{array} \right.\end{split}\]

où \(K\) est la matrice de Gramm \(K_{ij} = k(x_i, x_j)\) et \(e=(1, 1, \dots 1)^T\). Le centre est obtenu par \(g = \sum_{i=1}^{n}\alpha_i \phi(x_i)\). Un nouveau point \(x\) appartient au support si \(||\phi(x) - g|| \leq R^2\), ou :

\[K(x, x) - 2 \sum_{i=1}^{n} \alpha_i K(x_i, x) + \sum_{i,j=1}^{n}\alpha_i \alpha_j K(x_i, x_j) \leq R^2\]

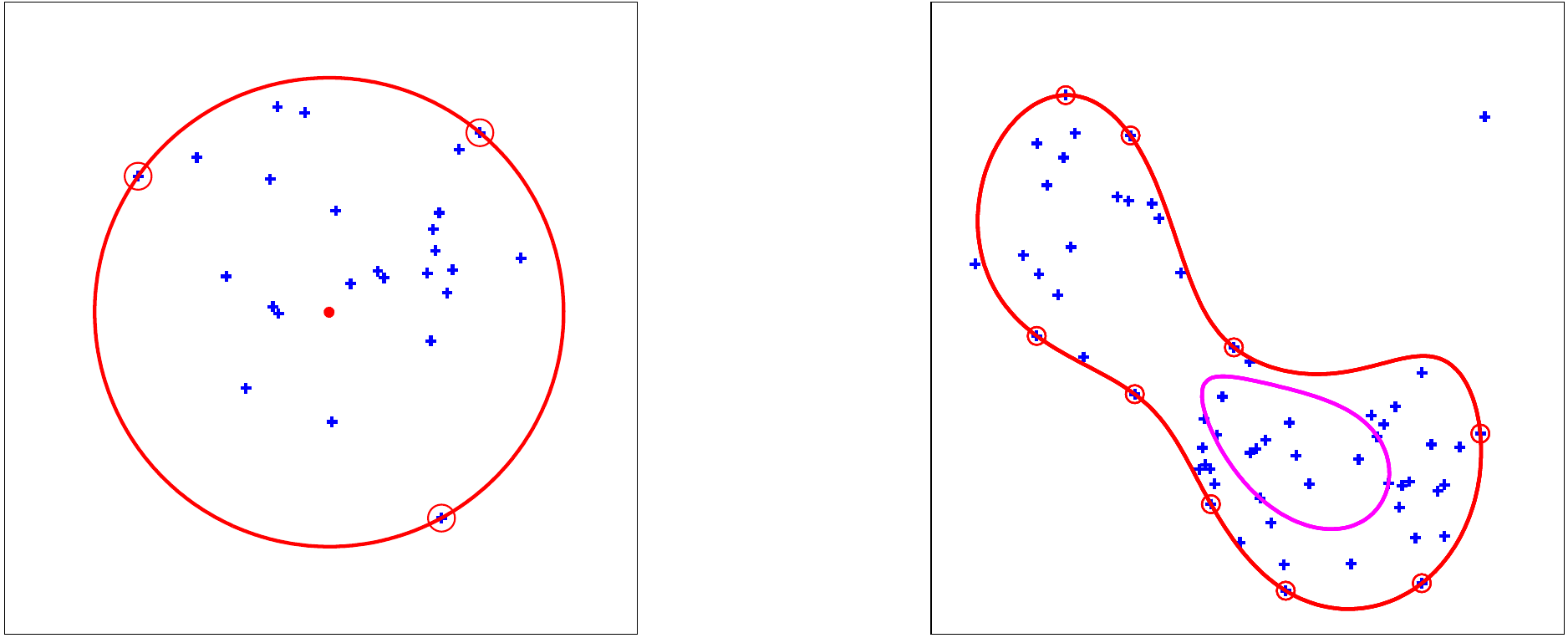
Fig. 65 Exemple SVDD : linéaire (à gauche) et noyau gaussien (à droite). A droite, le calcul a été fait pour deux valeurs de \(C\). Le point en haut à droite est un outlier (il est placé en dehors de l’enveloppe calculée).

One Class SVM (OCSVM)

Dans l’approche One Class SVM (OCSVM) de [SS01] il faut trouver, dans l’espace d’arrivée \(\mathcal{H}\), l’hyperplan le plus éloigné de l’origine qui sépare les données de l’origine.

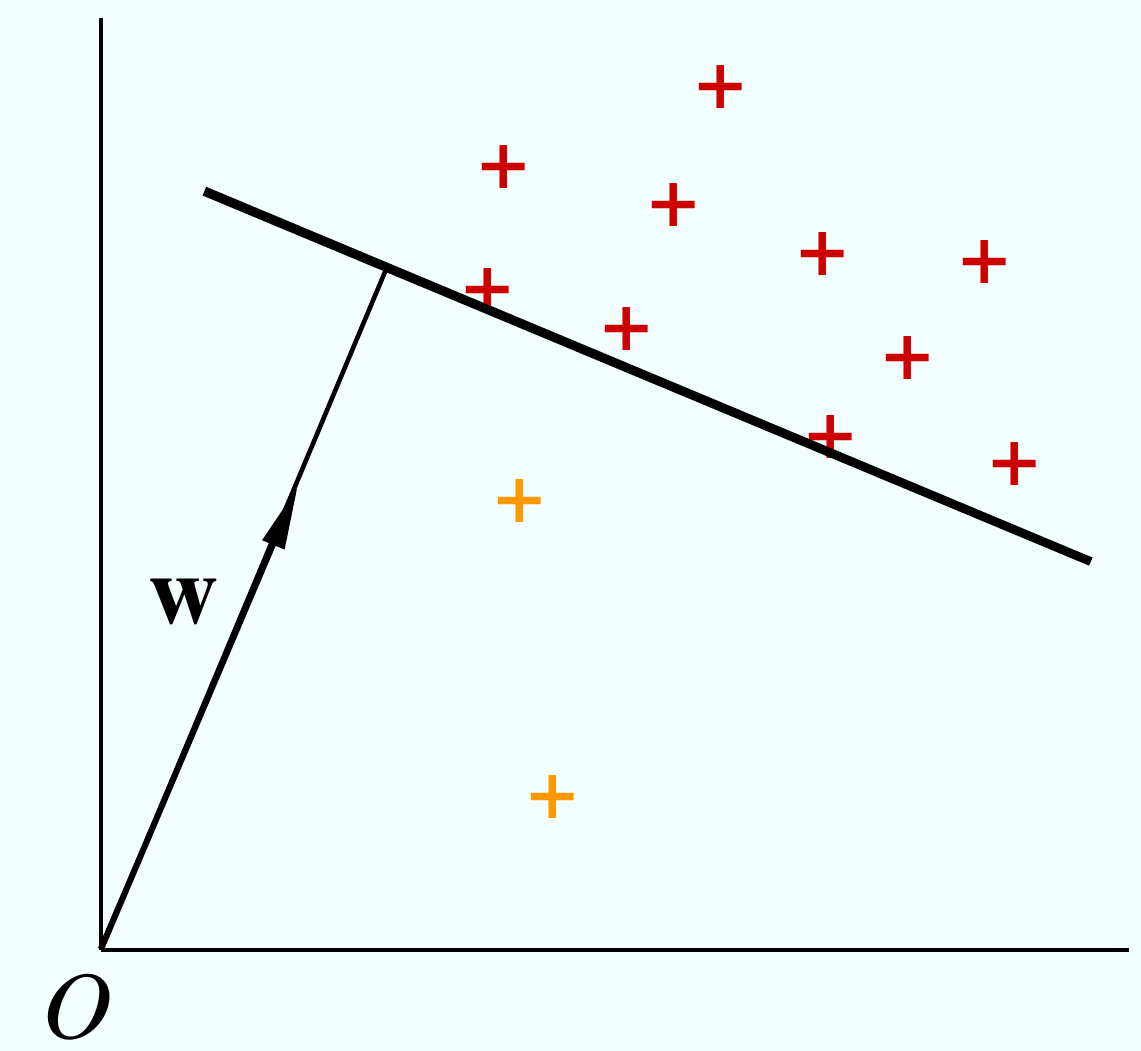
Fig. 66 L’approche One Class SVM (OCSVM) : chercher l’hyperplan le plus éloigné de l’origine qui sépare tous les points d’apprentissage (moins éventuellement les quelques ouliers).

Cela conduit au problème primal suivant (voir [SS01]) :

\[\begin{split}\left\{ \begin{array}{lll} \underset{w,\xi_i, \rho}{\min}\; \frac{1}{2} ||w||^2 + C \sum_{i=1}^n\xi_i -\rho \\ \textrm{avec :}\\ w\cdot x_i \geq \rho - \xi_i, i = 1, \dots, n\\ \xi_i \geq 0, i = 1, \dots, n \end{array} \right.\end{split}\]

où :

• la fonction de décision est donnée par : \(f(x) = \mathrm{sign}\left(\langle w, \phi(x)\rangle - \rho\right)\),

• \(\rho\) est la distance à l’origine,

• \(C = \frac{1}{\nu n}\) est un paramètre de régularisation qui permet de contrôler le nombre de outliers.

Le problème dual est le même que celui des SVDD avec le terme linéaire de la fonction coût en moins :

\[\begin{split}\left\{ \begin{array}{lll} \underset{\alpha}{\min}\; \frac{1}{2}\alpha^T K \alpha\\ \textrm{avec :}\\ e^t \alpha = 1\\ 0 \leq \alpha_i <= C, i = 1, \dots, n \end{array} \right.\end{split}\]

où :

• \(K\) est la matrice de Gramm \(K_{ij} = k(x_i, x_j)\) et \(e=(1, 1, \dots 1)^T\)

• la fonction de décision est donnée par :

  \[f(x) = \mathrm{sign}\left(\langle w, \phi(x)\rangle - \rho\right) = \mathrm{sign}(\sum_{i=1}^{n}\alpha_i K(x_i, x) - \rho)\]

  avec \(\rho = \langle w, \phi(x_s)\rangle = \sum_{i=1}^{n}\alpha_i K(x_i, x_s)\)

• \(C = \frac{1}{\nu n}\) est le paramètre de régularisation qui permet de contrôler le nombre de outliers.

Dans les deux formulations \(\nu \in (0, 1]\) et \(\nu n = 1/C\) peut être interprété comme :

• une borne supérieure pour la fraction de outliers,

• une borne inférieure pour la fraction de vecteurs de support.

Concernant la capacité de généralisation : la probabilité pour que des nouveaux exemples (tirages i.i.d. suivant la densité \(p(x)\)) soient en dehors du support déterminé est plus petite que la fraction de outliers dans les données d’apprentissage.

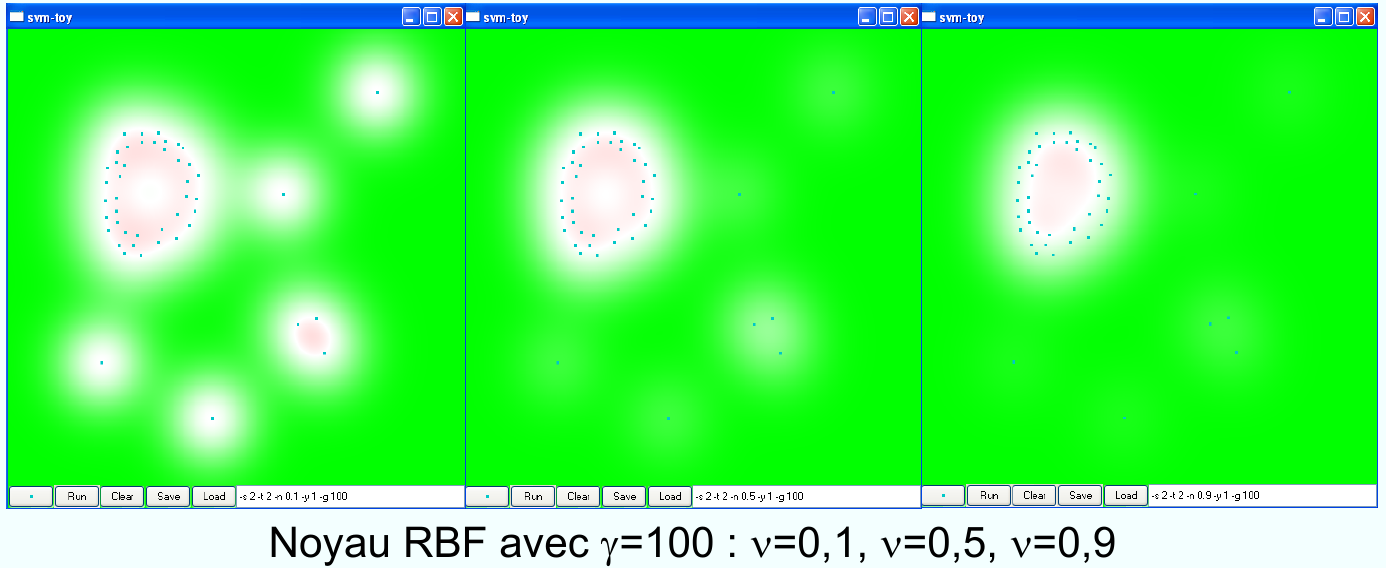
Fig. 67 Effet du paramètre \(\nu\) dans le OCSVM.

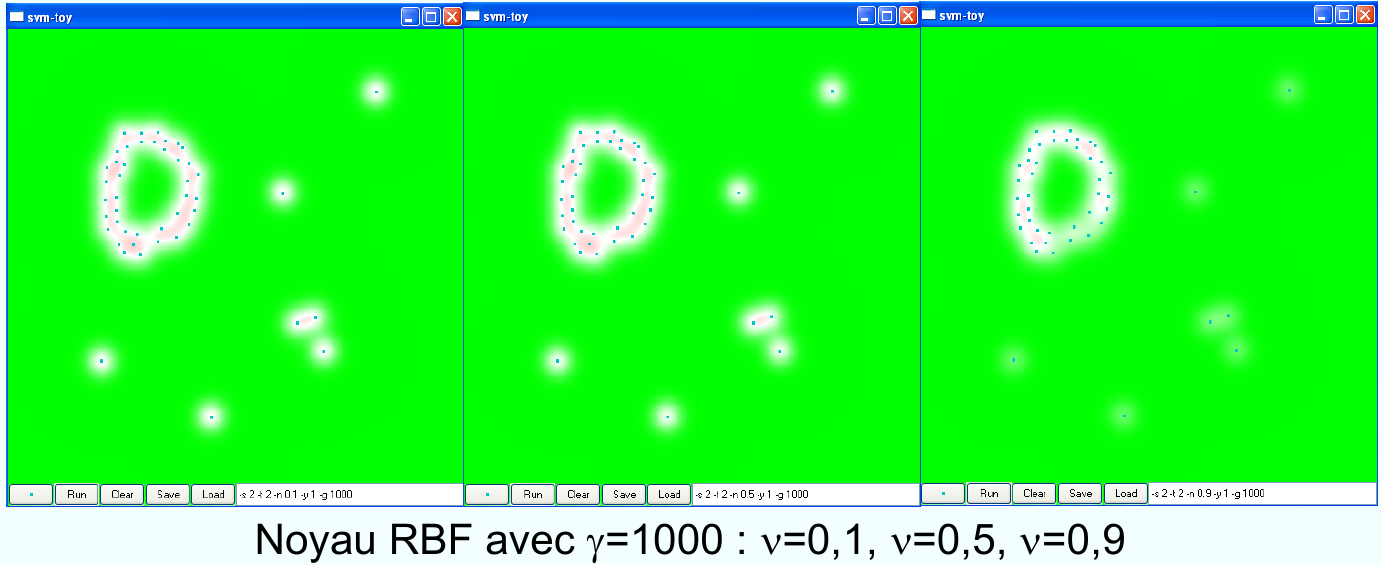
Fig. 68 Effet du paramètre \(\nu\) dans le OCSVM. Pour comparaison : le paramètre d’échelle du noyau \(\gamma\) a une valeur bien plus grande par rapport à la Fig. 67.

SVM pour la régression (SVR)

Les données d’apprentissage sont \(\mathcal{D} = \{(x_i, y_i); i = 1,\dots, n\}\), où \(x_i \in \mathcal{X}, y_i \in \mathbb{R}\). A la différence du problème de classification, où les \(y_i\) étaient des étiquettes de classe (valeurs -1 ou 1), ici les \(y_i\) ont des valeurs réelles. Le but est donc, étant donné une novelle observation \(x\) de prédire la valeur du \(y\) associé. C’est un problème plus difficile, car il faut apprendre à prédire les valeurs d’une fonction à partir d’un nombre fini d’échantillons.

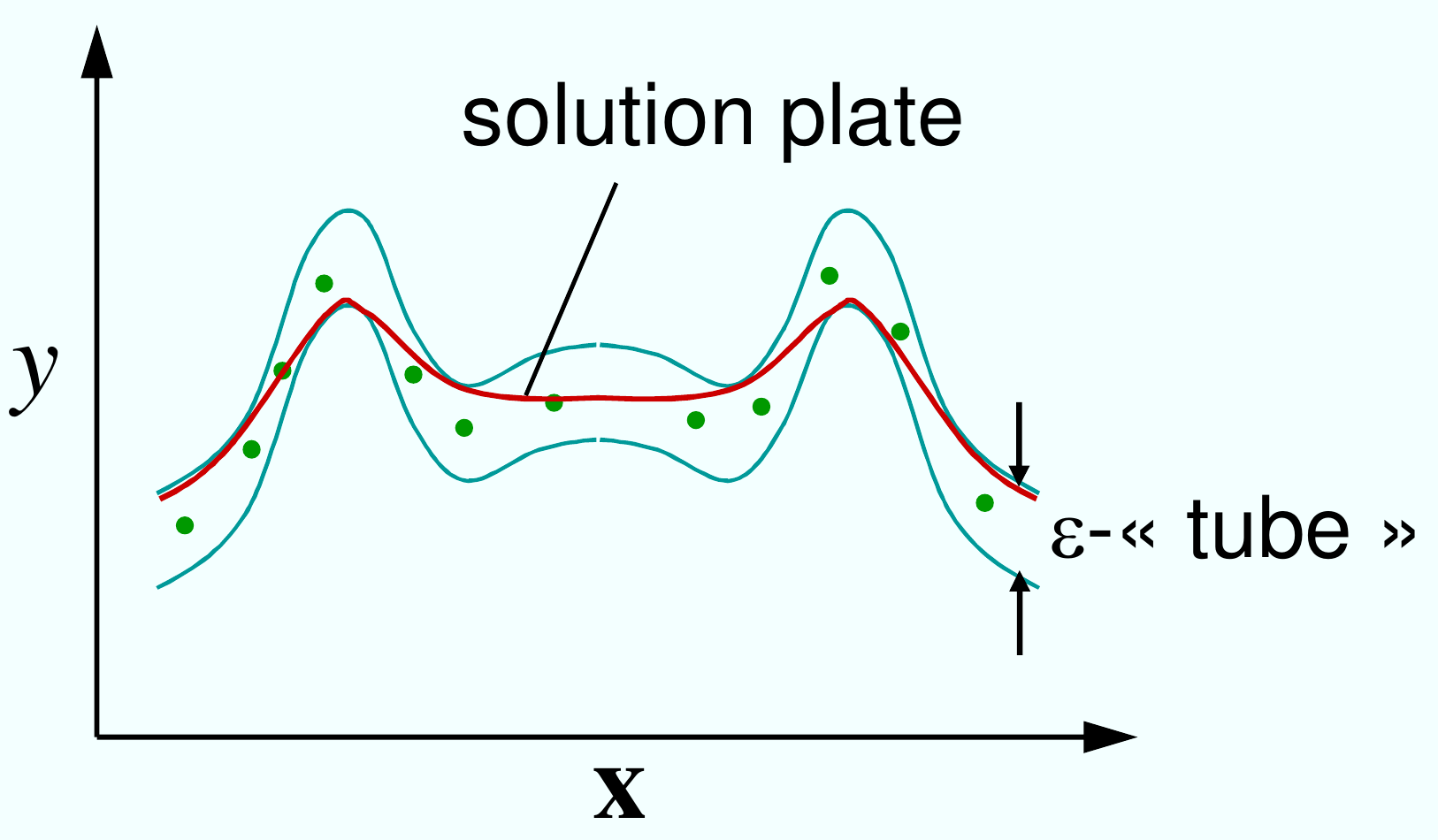
Fig. 69 SVM pour la régression : on cherche une solution aussi « plate » que possible sans s’éloigner trop des points d’apprentissage (en vert).

En régression \(\epsilon\)-SV on cherche donc une fonction \(f:\mathcal{X} \rightarrow R\) aussi « plate » que possible tel que \(|f(x_i) - y_i| < \epsilon\) pour tous les \(i\). Pour cela on considère les projections des points d’apprentissage dans l’espace d’arrivée \(\mathcal{H}\) et on cherche des solutions de la forme

\[f(x) = \langle w, \phi(x)\rangle + b\]

La condition d’aplatissement se traduit par la minimisation de \(||w||^2 = \langle w, w \rangle\).

La régression \(\epsilon\)-SV correspond à l’utilisation de la fonction de coût \(\epsilon\)-insensible :

\[\begin{split}|\xi|_\epsilon = \left\{ \begin{array}{ll} 0 \mathrm{\;si\;} |\xi| < \epsilon\\ |\xi| - \epsilon \mathrm{\;sinon\;}\\ \end{array} \right.\end{split}\]

Comme en discrimination, on accepte quelques erreurs au-delà de \(\epsilon\) et on introduit les « variables d’assouplissement » \(\xi_t\) et \(\xi_t^*\) :

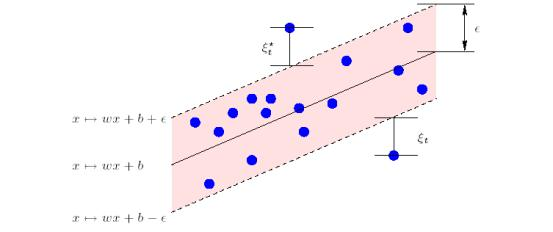
Le problème d’optimisation sera :

\[\begin{split}\left\{ \begin{array}{llll} \underset{w, b}{\min}\; \frac{1}{2} ||w||^2 + C \sum_{i=1}^n(\xi_i + \xi_i^*)\\ \textrm{avec :}\\ y_i - \langle w, \phi(x_i)\rangle - b \leq \epsilon + \xi_i, i = 1, \dots, n\\ \langle w, \phi(x_i)\rangle +b - y_i \leq \epsilon + \xi_i^*, i = 1, \dots, n\\ \xi_i, \xi_i^* \geq 0, i = 1, \dots, n \end{array} \right.\end{split}\]

La constante \(C > 0\) permet de choisir le point d’équilibre entre l’aplatissement de la solution et l’acceptation d’erreurs au-delà de \(\epsilon\)-SVM pour la régression. Avec les multiplicateurs de Lagrange on obtient le problème dual :

\[\begin{split}\left\{ \begin{array}{llll} \underset{\alpha, \alpha^*}{\min}\; \frac{1}{2}\sum_{i,j=1}^{n} (\alpha_i - \alpha_i^*)(\alpha_j - \alpha_j^*)K(x_i, x_j) + \epsilon\sum_{1=1}^{n} (\alpha_i + \alpha_i^*) - \sum_{1=1}^{n} y_i (\alpha_i - \alpha_i^*) \\ \textrm{avec :}\\ 0 \leq \alpha_i, \alpha_j \leq C,\; i,j = 1, \dots, n\\ \sum_{1=1}^n (\alpha_i - \alpha_i^*) = 0 \end{array} \right.\end{split}\]

Tous les points d’apprentissage à l’intérieur du \(\epsilon\)-tube ont \(\alpha_i = \alpha_i^* = 0\). Les points qui ont \(\alpha_i, \alpha_i^* \neq 0\) sont appelés vecteurs de support. Comme \(w = \sum_{1=1}^n (\alpha_i - \alpha_i^*)\phi(x_i)\), la fonction recherchée sera :

\[f(x) = \sum_{1=1}^n (\alpha_i - \alpha_i^*)K(x_i, x) + b\]

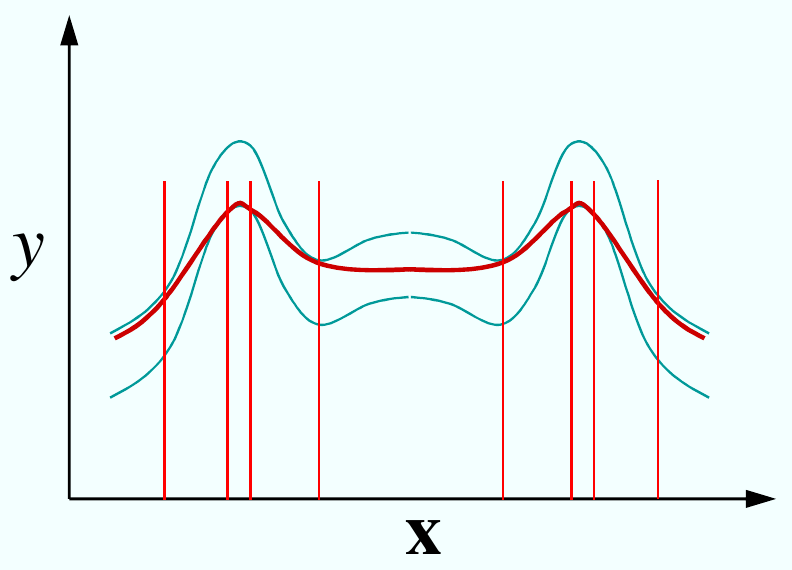
Fig. 70 Le choix du paramètre \(\epsilon\) est d’une grande importance pour éviter les phénomènes de sur- et sous-apprentissage.

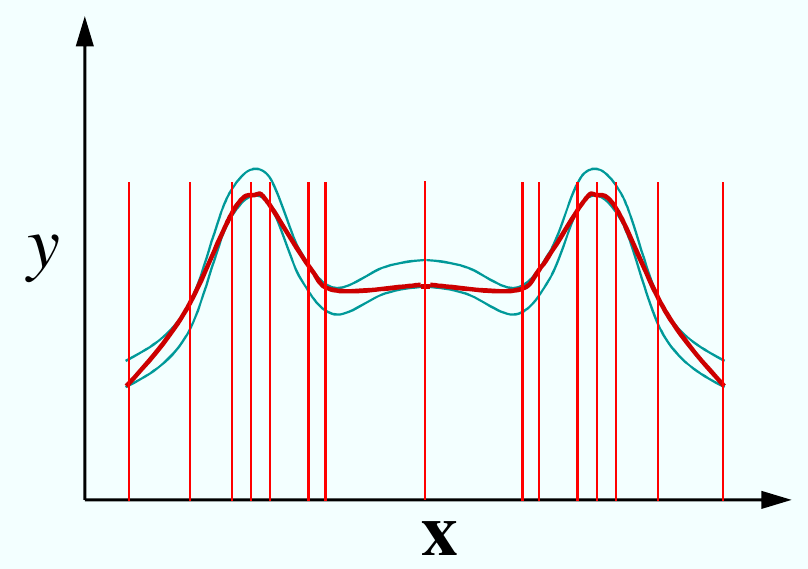
Fig. 71 Des valeurs trop petites du paramètre \(\epsilon\) forcent la fonction approximée de suivre les détails (bruit) de l’échantillon. Ceci conduit au problème de sur-apprentissage.

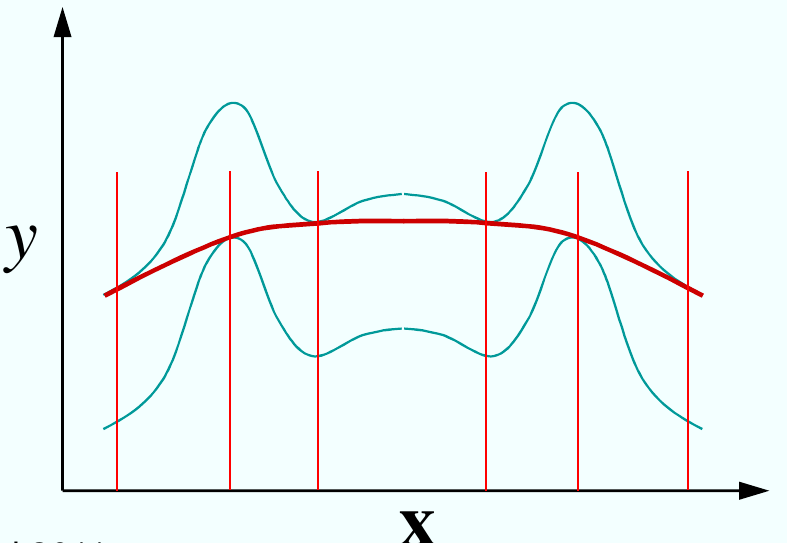
Fig. 72 Des valeurs trop grandes du paramètre \(\epsilon\) mènent à une fonction trop lissée (problème de sous-apprentissage).

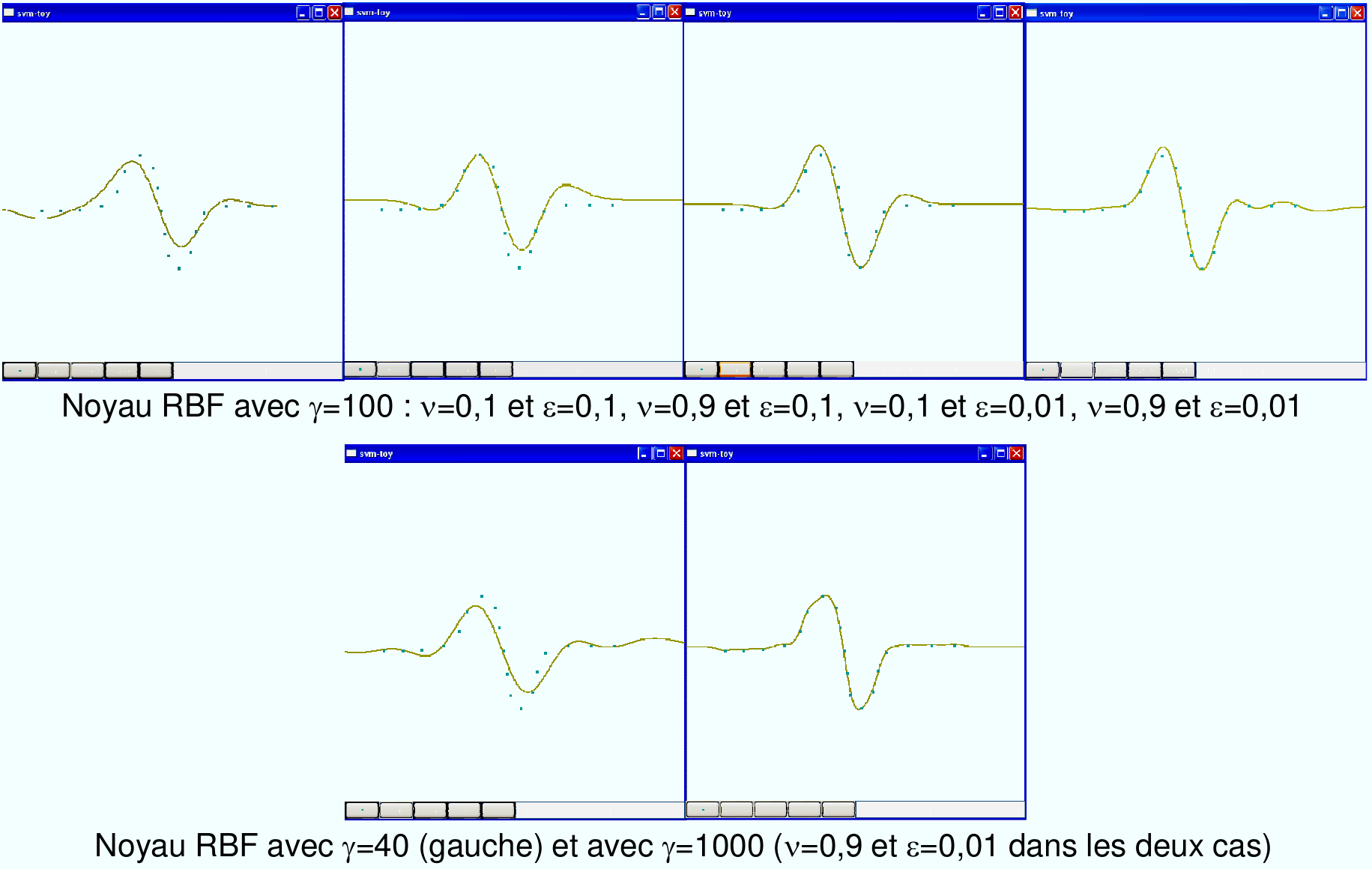
Fig. 73 L’impact des paramètres \(\nu\) et \(\epsilon\) sur un problème de régression (exemple produit avec l’outil SVM-Toy).

Autres algorithmes à noyaux

Pratiquement, tout algorithme qui utilise des produits scalaires entre les échantillons peut être « non-linéarisé » par le « truc des noyaux ». Quelques exemples notables :

• Kernel PCA (Principal Component Analysis), voir [SS01] ;

• Kernel CCA (Canonical Correlation Analysis), voir [HSS03] ;

• Kernel FDA (Factorial Discriminant Analysis), voir [RS00].

Applications des SVM

Les machines à vecteurs de supports ont l’avantage de ne pas nécessiter le réglage de beaucoup de paramètres et ont été appliquées avec grand succès dans de nombreux domaines :

• Finance (évolution des prix, valeurs en bourse, etc.)

• Structure des protéines (protein folding)

• Génomique (microarray gene expression data)

• Reconnaissance de visages

• Détections des catastrophes, forecasting

• Images satellite et surveillance

• Diagnostic médical (cancer du sein)

• En physique, par ex. Particle and Quark-Flavour Identification, High Energy Physics (Classifying LEP Data with Support Vector Algorithms by Schölkopf et al. AIHENP’99).

Références : livres, articles, web

SC08

Steinwart, Christmann, Support Vector Machines, Springer 2008.

SS01(1,2,3)

Scholkopf, Smola, Learning with Kernels, The MIT Press, 2001.

HTF06

Hastie, Tibshirani, Friedman, The elements of statistical learning: data mining, inference, and prediction, New York, Springer Verlag, 2006.

WikiStat

Machines à vecteurs supports (WikiStat), http://wikistat.fr

TD04(1,2)

Tax and Duin, Support Vector Data Description, Machine Learning, 54(1), 2004.

HSS03

Hardoon, Szedmak, Shawe-Taylor, Canonical correlation analysis; an overview with application to learning methods, Technical Report, University of London, 2003.

RS00

Roth, Steinhage, Nonlinear discriminant analysis using kernel functions, Advances in Neural Information Processing Systems, 2000.