Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.

Cours - Introduction à l’apprentissage profond (deep learning)

[Diapositives du cours]

Des données non-structurées de grande dimension

La démocratisation de l’informatique a conduit à la numérisation de grands volumes de données. Une spécificité des deux dernières décennies est la nécessité de stocker et de traiter des grands volumes de données non-structurées : images, vidéos, sons, textes et, de manière générale, signaux de tous types. À titre d’exemple, les archives de la BBC représentent environ 2,4 millions de cassettes et 600 000 bobines, pour un total de plus de 600 000 heures de film. Pouvoir accéder à ces données, les indexer et les classer est donc essentiel. Cela signifie que les systèmes informatiques doivent donc être en mesure d’effectuer de la reconnaissance au sein de ces données, afin d’identifier des propriétés sémantiques (type de film, présence d’un acteur, langue du sous-titrage, etc.) d’intérêt pour les utilisateurs.

Néanmoins, la représentation numérique des données est prévue pour être aisément manipulable par une machine mais est rarement facile d’interprétation pour un humain. Par exemple, les images sont encodées sous forme de matrices de pixels. Les pixels représentent l’intensité lumineuse reçue en un point de l’image. Ces valeurs sont donc sensibles aux variations d’illumination ou de point de vue. Ces variations ne changent pourtant pas la sémantique de l’objet: un l’observateur humain identifiera un cheval, qu’il soit vu de jour comme de nuit, de face comme de profil.

La question est donc de déterminer une « bonne » représentation des données, qui permette d’encoder les informations utiles (quel objet est présent dans l’image ?) en éliminant le superflu (l’objet est légèrement de côté).

Apprentissage statistique classique

L’approche traditionnelle consiste à effectuer de l’ingénierie des caractéristiques (feature engineering) afin de transformer la donnée non-structurée en une représentation intermédiaire, plus à même d’être utilisée en entrée d’un algorithme d’apprentissage. Ces caractéristiques sont généralement qualifiées d’expertes ou hand-crafted, car elles sont conçues par l’humain à partir de connaissances spécialisées sur les données.

Il est possible de résumer le processus classique menant des données à la décision de la façon suivante :

1. Choix de la représentation/détermination de caractéristiques expertes

   • descripteurs images (SIFT, HOG)

   • coefficients spectraux pour l’audio (MFCC)

   • moyenne glissante, dérivée première, dérivée seconde pour les séries temporelles

2. Création d’un jeu de données, séparation apprentissage/validation/test

3. Entraînement d’un ou plusieurs modèles décisionnels, sélection du meilleur modèle

4. Évaluation des performances du modèle final

Il est clair que l’étape 1 est cruciale dans cette méthodologie : si les informations utiles à la modélisation décisionnelle ne sont pas représentées dans les caractéristiques choisies, alors les performances du modèle seront nécessairement dégradées. Toutefois, comme nous l’avons vu précédemment, l’inclusion d’informations redondantes, voire d’informations bruitées, peut également réduire les performances du modèle. Autrement dit, il peut-être nécessaire de répéter ce processus afin d’évaluer non seulement le choix des hyperparamètres des modèles, mais aussi l’impact de la représentation choisie pour encoder les données. On peut se demander s’il ne serait pas possible d’adapter automatiquement la représentation des données au problème de modélisation décisionnelle qui nous intéresse. En effet, la représentation idéale d’une image n’est probablement pas la même selon que la tâche : un humain n’utilise pas les mêmes informations pour reconnaître un chat d’un chien que pour estimer la distance qui sépare deux voitures. Cette co-adaptation est justement rendue possible par l’apprentissage profond [1LBH15].

Réseaux de neurones artificiels

Mathématiquement, un neurone artificiel est une fonction de plusieurs variables qui réalise la combinaison linéaire de ses entrées par des pondérations arbitraires. Considérons un vecteur \(\mathbf{x} \in \mathbb{R}^m = \{x_1, x_2, \dots, x_m\}\). Un neurone opérant sur le vecteur \(\mathbf{x}\) possède \(m\) poids notés \(w_1\) jusqu’à \(w_m\) qui représentant l’importance donnée à leur entrée respective \(x_j\). La sortie du neurone artificiel est un réel \(s \in \mathbb{R}\) obtenu par somme pondérée :

\[s = \sum_{i=1}^m w_i x_i\]

Cette équation peut également se représenter sous forme matricielle par la multiplication entre le vecteur-ligne \(\mathbf{w}\) et le vecteur-colonne \(\mathbf{x}\):

\[s = \mathbf{w}^T \mathbf{x} = \begin{bmatrix} w_1 & w_2 & \dots & w_m\end{bmatrix} \begin{bmatrix} x_1\\ x_2 \\ \vdots \\ x_m\end{bmatrix}\]

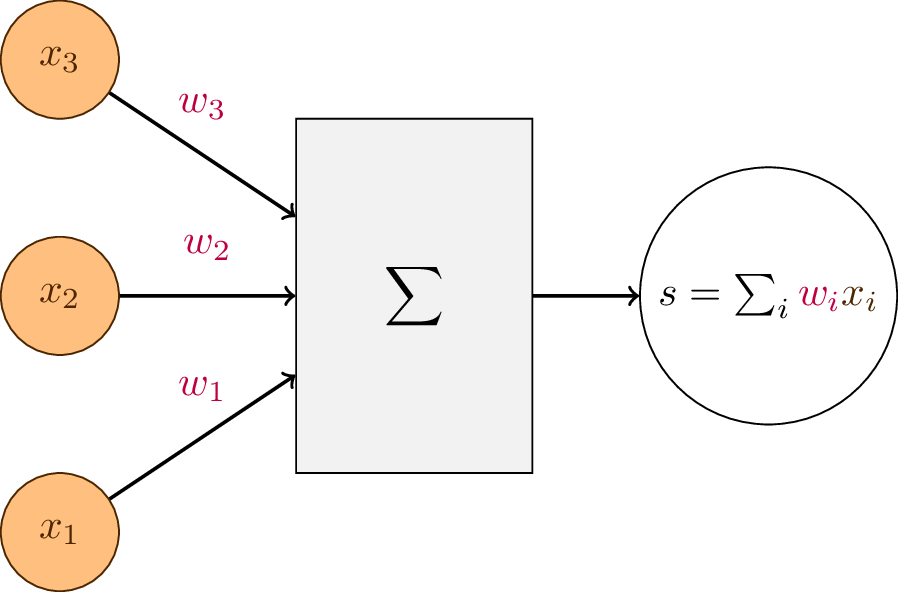
Fig. 83 Schéma d’un neurone formel simplifié. L’activation en sortie du neurone est la somme pondérée des activations en entrée.

L’analogie biologique est la suivante : \(\hat{y}\) est l’activation de sortie du neurone artificiel. Cette activation est obtenue en cumulant les activations des neurones d’entrée (\(x_i\)) multipliée par le poids de la synapse qui relie les deux neurones, c’est-à-dire \(w_i\).

En général, on munit le neurone artificiel d’un biais \(b \in \mathbb{R}\), de sorte à ce que la fonction modélisée soit une fonction affine, c’est-à-dire une fonction linéaire suivie d’une translation :

\[s = \mathbf{w}^T \mathbf{x} + b\]

Le neurone peut également être doté d’une fonction de transfert, aussi appelée fonction d’activation. On notera cette fonction \(\phi : \mathbb{R} \rightarrow \mathbb{R}\). Elle transforme la somme pondérée \(s\) en une activation \(z = \phi(s)\). L’expression du neurone artificiel « complet » est donc :

\[z = \phi\left(\mathbf{w}^T \mathbf{x} + b\right)\]

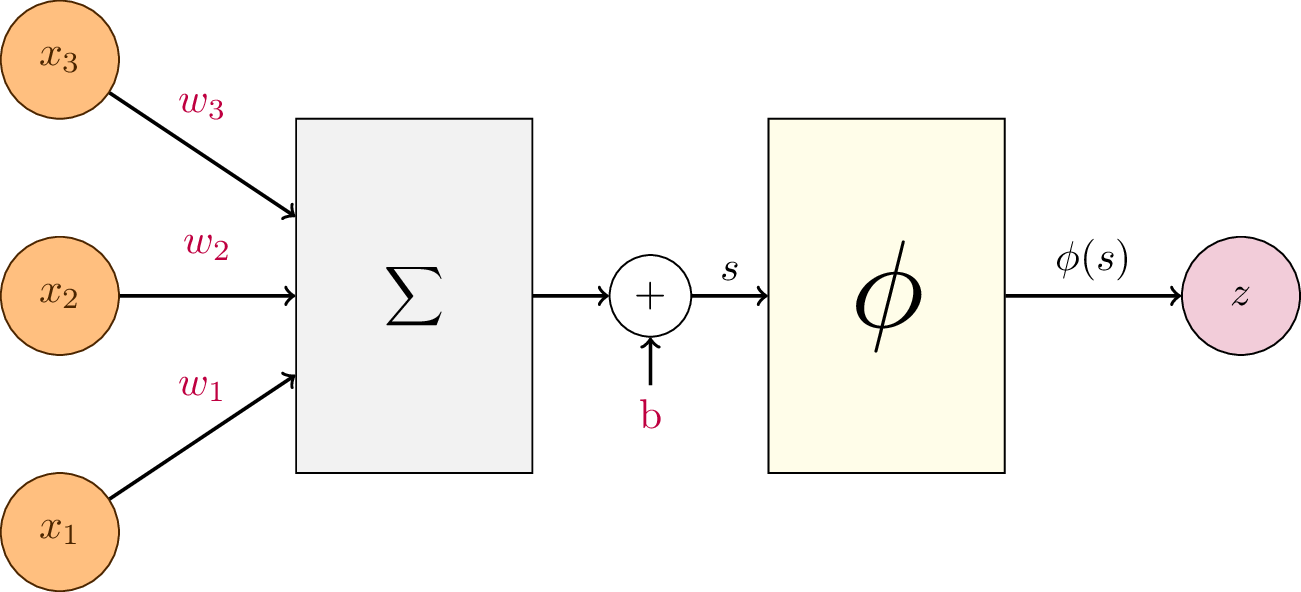
Fig. 84 Schéma d’un neurone formel. Le neurone réalise la somme pondérée des activations en entrée, plus un biais. Cette quantité passe ensuite dans une fonction de transfert \(\phi\), dite fonction d’activation.

Dans ce formalisme, les poids des connexions synaptiques \(\mathbf{w}\) et le biais \(b\) sont des paramètres du neurone artificiel, qu’il nous faudra déterminer par la suite.

Note

Dans de rares cas, le biais est directement compris dans les poids des connexions synaptiques en ajoutant une dimension additionnelle aux entrées, dont la valeur est constante est égale à 1 :

\[s = \mathbf{w}^T \mathbf{x} = \begin{bmatrix} w_1 & w_2 & \dots & w_m & b\end{bmatrix} \begin{bmatrix} x_1\\ x_2 \\ \vdots \\ x_m\\ 1\end{bmatrix}\]

C’est un simple changement de notation adopté par quelques auteurs. Nous conserverons notre convention précédente (poids et biais séparés) dans la suite du cours.

De nombreuses fonctions d’activation différentes peuvent être utilisées et il n’y a pas de règle concernant leur usage. Nous verrons plus tard quelles peuvent être les propriétés souhaitables pour les fonctions d’activation. En voici quelques exemples :

• Fonction identité: \(\operatorname{Id}(x) = x\)

• Échelon de Heaviside: \(H(x) = \begin{cases} 1 & \text{si}~x \geq 0\\ 0 & \text{sinon}\end{cases}\)

• Sigmoïde: \(\sigma(x) = \frac{1}{1 + e^{-x}}\)

• Tangente hyperbolique: \(\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\)

• Fonction linéaire rectifiée: \(\operatorname{ReLU}(x) = \begin{cases} x & \text{si}~x \geq 0\\ 0 & \text{sinon}\end{cases}\)

Le choix de la fonction d’activation est un hyperparamètre. Cette fonction d’activation est décidée au départ et ne changera pas lors de l’apprentissage.

Perceptron

Un tel neurone artificiel permet d’ores et déjà de modéliser différentes fonctions. Par exemple, il est possible d’effectuer de la régression. Si \(\phi\) est la fonction identité, alors chercher les paramètres du neurone formel qui minimisent l’erreur quadratique moyenne entre la sortie \(z\) et des valeurs de vérité terrain \(y\) est un problème classique de régression linéaire. Pour la classification, il faut se doter d’une fonction d’activation permettant de transformer la sortie continue \(z\) en une prédiction catégorielle. Un neurone formel permet de réaliser une classification binaire à l’aide de l’échelon de Heaviside, par exemple. En effet, l’échelon renvoie 0 ou 1 selon que l’activation \(z\) est positive ou négative. Cela permet donc de définir une frontière de classification, obtenue par l’équation

\[\mathbf{w}^T \mathbf{x} + b = 0\]

c’est-à-dire un hyperplan séparateur qui coupe l’espace d’entrée en deux. Ce modèle, introduit par , est appelé Perceptron. Par exemple, en dimension 2:

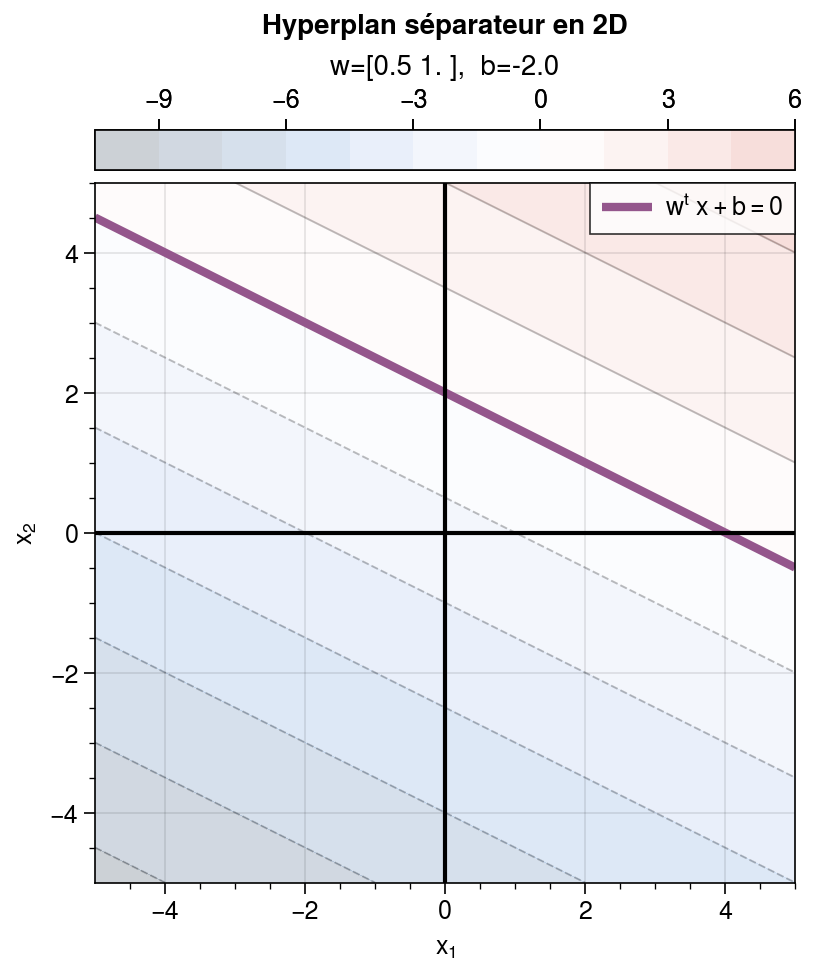
Représentation de l’activation du perceptron pour une entrée \(\mathbf{x} = (x_1, x_2)\) en deux dimensions. En seuillant à 0, le contour obtenu est la droite (en violet) d’équation \(\mathbf{w}^T \mathbf{x} + b = 0\) qui sépare le plan en deux. Remarquons que changer le biais \(b\) en sortie permet de déplacer la droite dans le plan, en choisissant l’une de ses parallèles, d’équation \(\mathbf{w}^T \mathbf{x} + b = \alpha\). Autrement dit, le biais permet de contrôler le seuil d’activation à partir duquel l’échelon de Heaviside change de valeur.

Le neurone formel réalise une classification binaire linéaire, équivalente à celle d’un machine à vecteur de support. La frontière de séparation est un hyperplan (une droite en 2D, un plan en 3D, etc.):

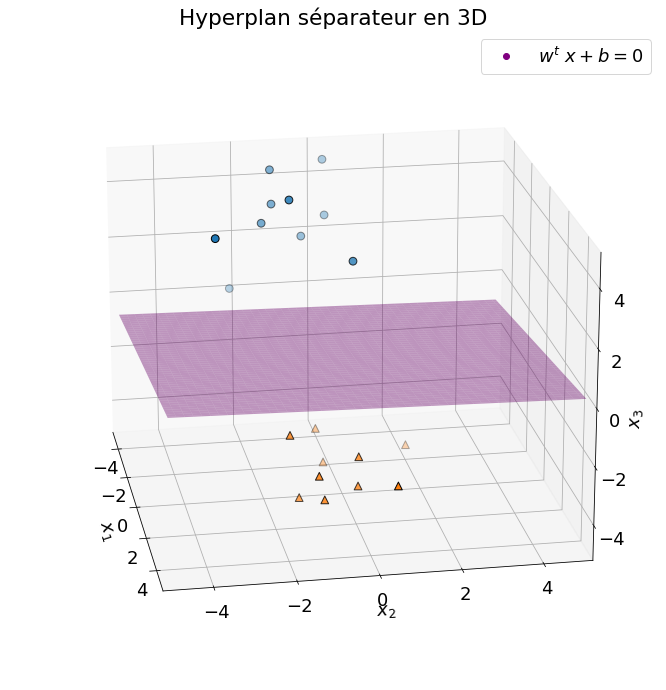
Représentation du plan obtenu à partir de l’équation \(\mathbf{w}^T \mathbf{x} + b = 0\) pour une entrée \(\mathbf{x} = (x_1, x_2, x_3)\) à trois dimensions.

En pratique, on seuille plutôt non pas l’échelon de Heaviside mais la sigmoïde. Les valeurs prises par la sigmoïde étant entre 0 et 1 (\(\sigma(z) \in [0,1]\)), cela permet d’interpréter la sortie du neurone comme une probabilité. Le seuil est alors habituellement fixé à \(0.5\). Par exemple, pour un problème de classification binaire, on interprètera la sortie de la sigmoïde comme étant la probabilité \(p(\operatorname{classe}(\mathbf{x}) = 1\), ce qui donne pour règle de décision :

\[\operatorname{classe}(\mathbf{x}) = \begin{cases} 1 & \text{si}~\sigma(\mathbf{w}^T \mathbf{x} + b) \geq 0.5\\ 0 & \text{sinon}\end{cases}\]

La sigmoïde est une approximation « lisse » de l’échelon de Heaviside. Il est notamment possible d’ajouter un facteur multiplicateur \(a\) dans l’exposant pour contrôler la pente du régime linéaire autour de zéro :

\[\sigma(x) = \frac{1}{1 + e^{-ax}}\]

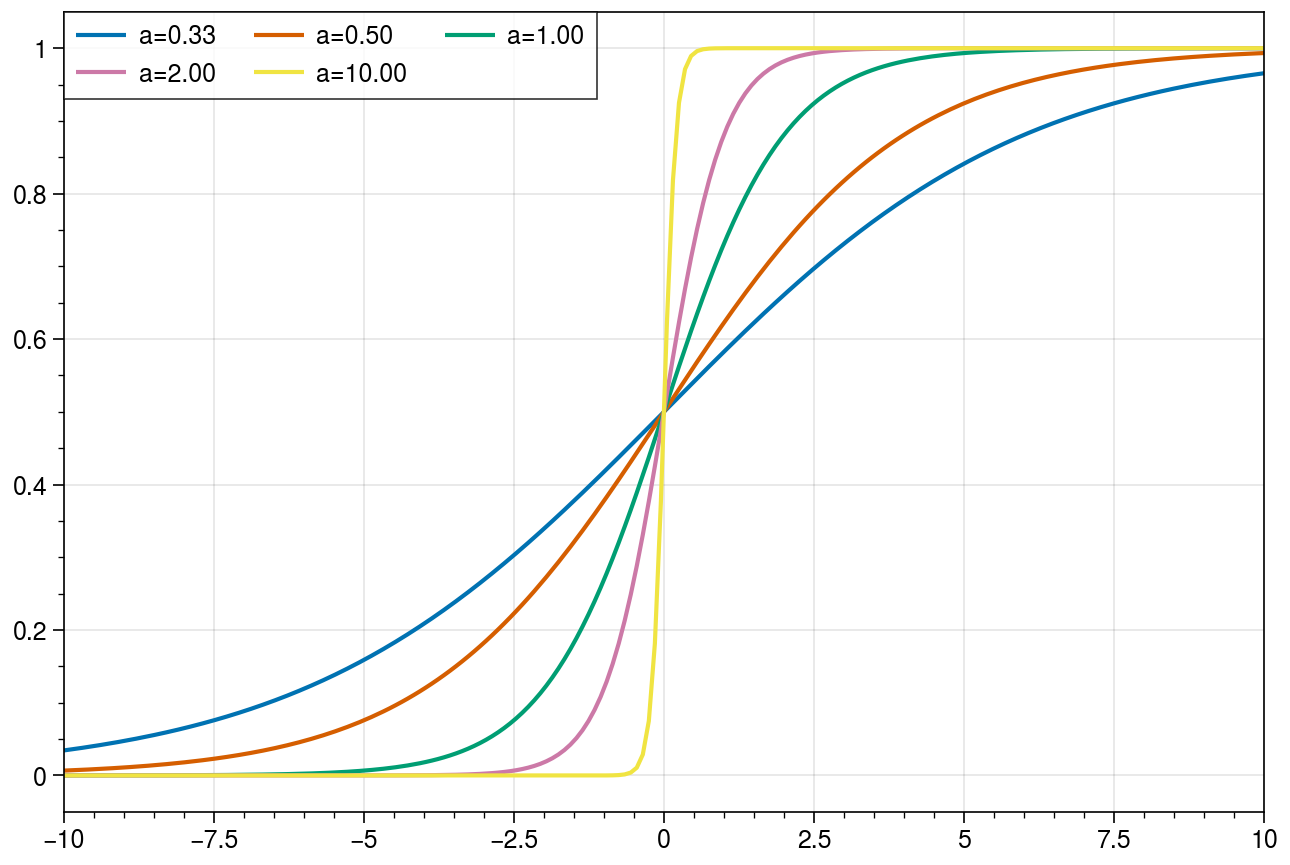
Évolution de l’activation sigmoïde pour différentes valeurs de \(a\) dans l’équation \(\sigma(x) = \frac{1}{1 + e^{-ax}}\)

La capacité de discrimination du neurone formel est pour l’instant limitée à la classification binaire. Qui plus est, les frontières obtenues sont des hyperplans, il s’agit donc d’un classifieur linéaire. Nous allons voir par la suite comment étendre les neurones artificiels à plusieurs classes, et surtout comment étendre cette famille de modèles aux problèmes non-linéaires.

Pour l’instant, notre ensemble de neurones artificiels est limité à sa plus simple expression : un nombre arbitraire de neurones d’entrés sont connectés à un unique neurone de sortie. Comment gérer le cas où la fonction \(f\) que l’on cherche à modéliser renvoie plusieurs variables ? La solution consiste à utiliser plusieurs neurones de sortie. Chaque neurone de sortie sera alors connecté à tous les neurones d’entrée. Cela revient en réalité à avoir plusieurs neurones en parallèle, chacun avec ses propres connexions synaptiques.

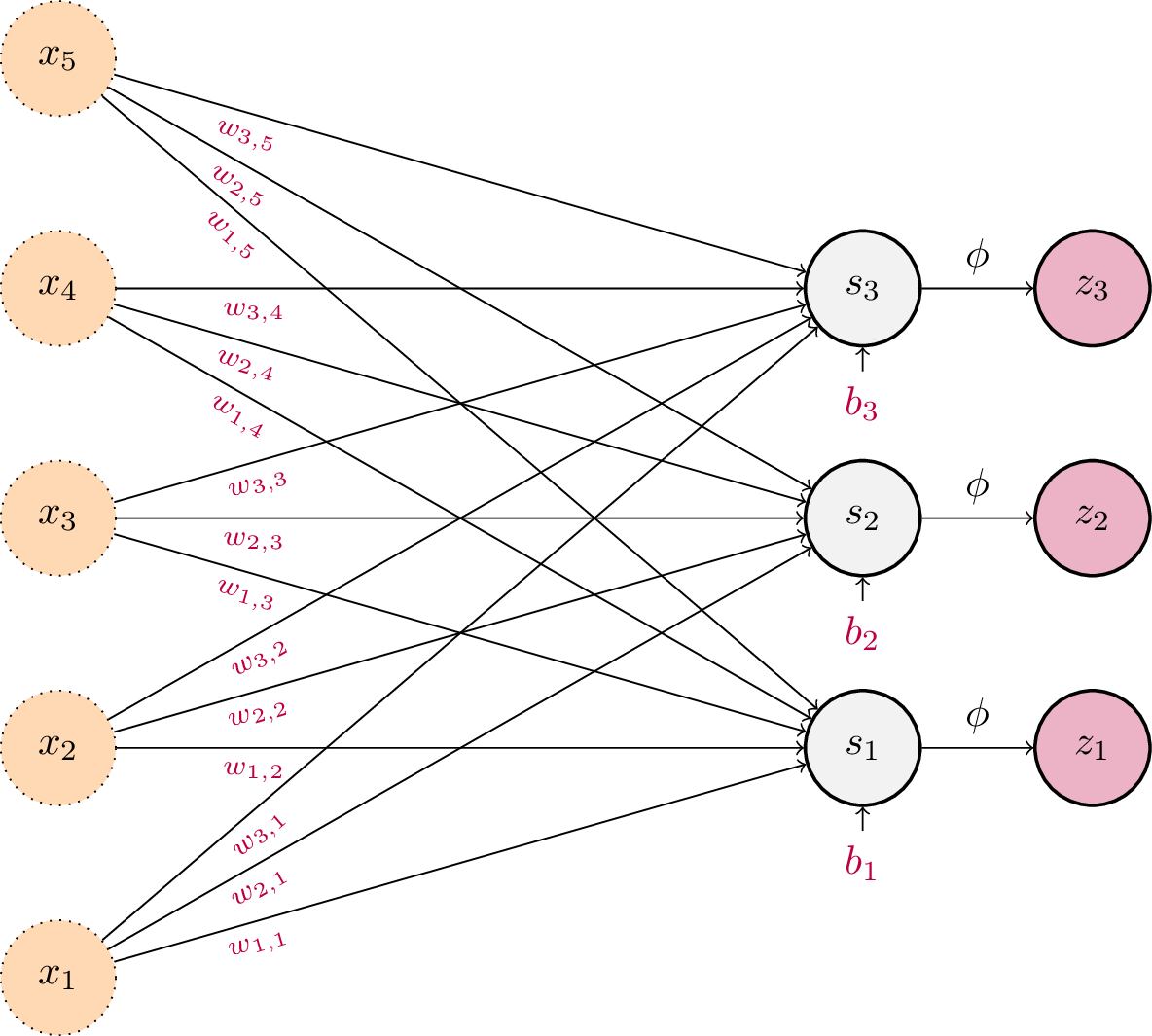
Schéma d’un Perceptron. Les entrées sont de dimension 5 et les sorties de dimension 3. Chaque neurone de sortie dispose de son propre vecteur de poids \(\mathbf{w_j}\) et de son biais scalaire \(b_j\).

Chaque sortie \(\mathbf{z}_j\) du perceptron s’obtient à l’aide de l’équation habituelle d’un neurone formel, à l’exception que les poids \(\mathbf{w_j}\) et le biais \(b_j\) dépendent désormais de l’indice \(j\) de la sortie considérée :

\[z_j = \phi\left(\mathbf{w_j}^T \mathbf{x} + b_j\right)\]

Cette équation peut se réécrire matriciellement pour englober toutes les sorties dans un unique vecteur \(\mathbf{z}\) :

\[\mathbf{z} = \phi\left(\mathbf{W} \mathbf{x} + \mathbf{b}\right)\]

avec, en notant \(m\) la dimension des entrées et \(k\) la dimension des sorties :

\[\mathbf{W} = \begin{bmatrix} \mathbf{w_1}^T \\ \mathbf{w_2}^T \\ \vdots \\ \mathbf{w_k} \end{bmatrix} = \begin{pmatrix} w_{1,1} & w_{1,2} & \dots & w_{1,m} \\ w_{2,1} & w_{2,2} & \dots & w_{2,m} \\ \vdots & \cdots & \cdots & \vdots \\ w_{k,1} & w_{k,2} & \dots & w_{k,m} \\\end{pmatrix} ~~~\text{et}~~~ \mathbf{b} = [b_1, b_2, \dots, b_k]\]

Régression logistique

Pour étendre la classification à trois classes et plus, il faut généraliser la sigmoïde vue précédemment dans le cas binaire. Pour ce faire, nous pouvons utiliser la fonction d’activation dite softmax :

\[\mathbf{z}_i = \frac{e^{s_i}}{\sum_{j=1}^k e^{s_j}}\]

Cette fonction d’activation est un peu particulière puisque, contrairement à celles vues précédemment, sa valeur pour l’élément \(i\) dépend également des valeurs pour les éléments \(j \neq i\). L’intérêt du softmax est d’obtenir une fonction \(f: \mathbb{R}^k \rightarrow \mathbb{R}^k\) qui permet d’interpréter \(f(s)_i\) comme une probabilité conditionnelle \(P(i|\mathbf{x})\) pour une observation \(\mathbf{x}\) d’appartenir à la classe \(i\). La seule contrainte est que la somme des probabilités valent 1, ce qui est obtenu par la normalisation au dénominateur.

Preuve

\[\sum_{i=1}^k \mathbf{z}_i = \sum_{i=1}^k \frac{e^{s_i}}{\sum_{j=1}^k e^{s_j}} = \frac{\sum_{i=1}^k e^{s_i}}{\sum_{j=1}^k e^{s_j}} = 1.\]

La combinaison d’un perceptron et de l’activation softmax est un modèle de classification multi-classes appelé la régression logistique. Bien qu’il s’agisse toujours d’un modèle linéaire, les frontières de décision pour les classes prises deux à deux étant à nouveau des hyperplans, il s’agit cette fois d’un classifieur multi-classes. La linéarité reste problématique dans la mesure où peu de problèmes réels admettent une solution linéaire. Un exemple frappant est le problème du XOR (OU exclusif) [1MP69], présenté ci-dessous :

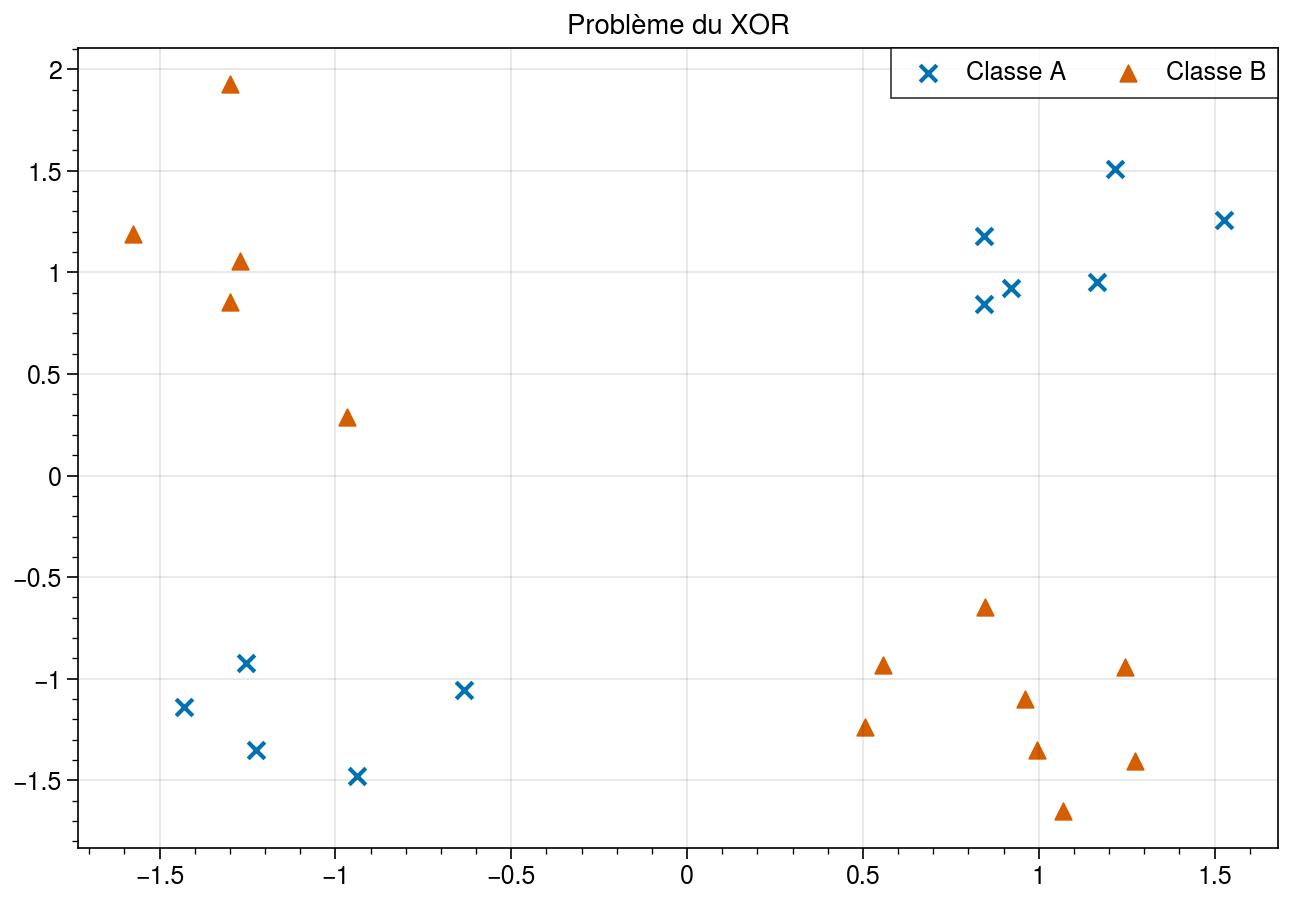
Problème du XOR en dimension 2. Les deux classes A et B ne sont pas linéairement séparables: il n’existe pas de frontière de séparation (une droite) qui permette de délimiter d’un côté tous les points de la classe A et de l’autre otus les points de la classe B.

En dépit de sa simplicité, le problème du XOR ne peut pas se résoudre à l’aide d’un classifieur linéaire. Il n’existe donc pas de perceptron qui soit en mesure de le résoudre ! Nous avons donc besoin d’introduire de la non-linéarité dans nos neurones artificiels si nous voulons résoudre des problèmes décisionnels qui ne soient pas triviaux.

Perceptron multi-couche

Pour aller plus loin, il est nécessaire de construire un réseau de neurones plus complexe. Pour ce faire, posons-nous la question suivante : pourrait-on ajouter un neurone formel dont l’entrée ne soit pas les observations, mais la sortie d’un autre neurone ? Autrement dit, cela reviendrait à ajouter une nouvelle « couche » de neurones en sortie du perceptron. Cette couche intermédiaire sera dite couche cachée, car elle n’est pas « visible » de l’extérieur. Elle s’intercale seulement entre les données d’entrée et les prédictions de sortie. Cela nous permet de définir le perceptron multi-couche (PMC).

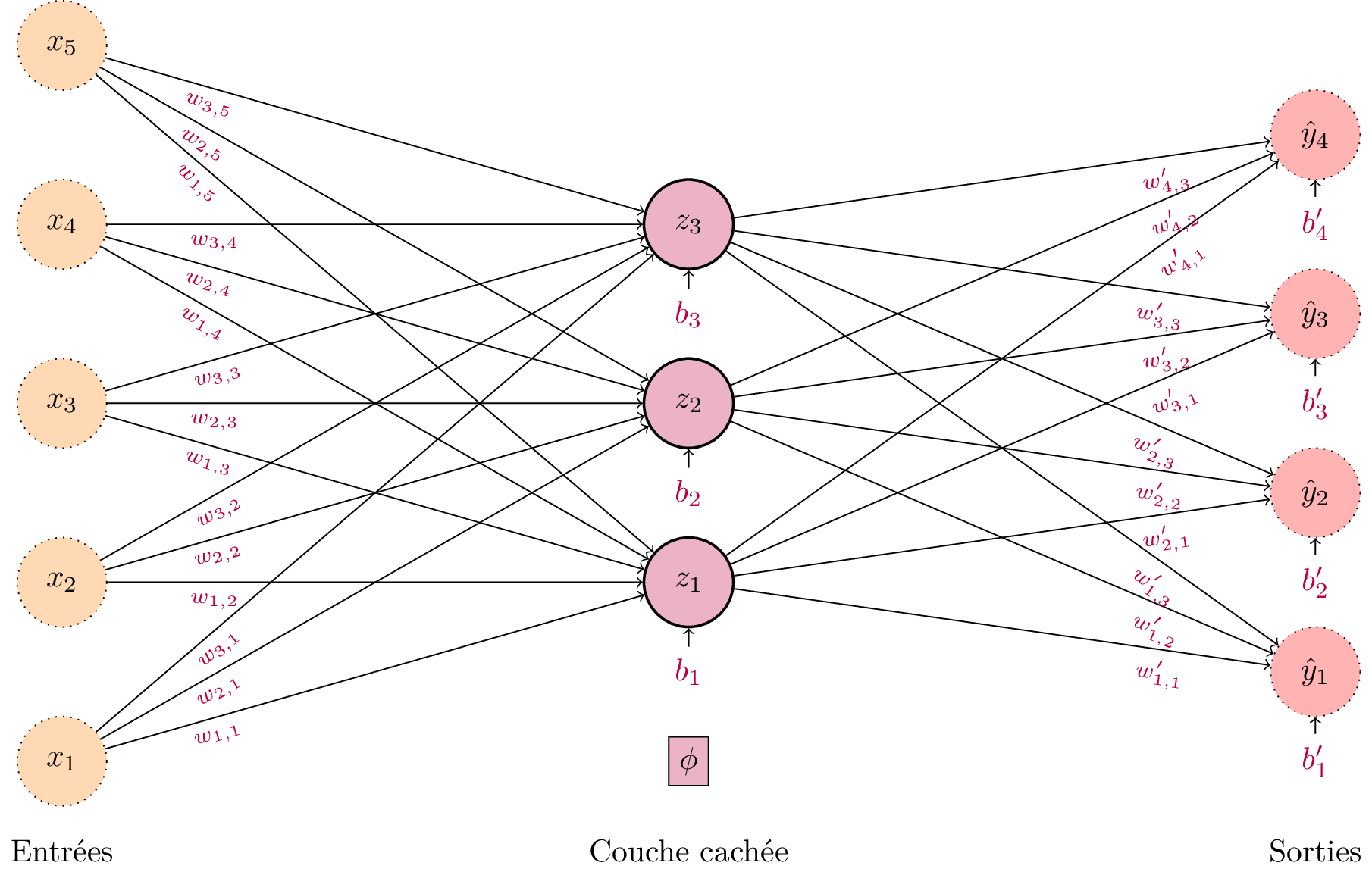
Schéma d’un perceptron multi-couche. Les entrées sont de dimension 5 et les sorties de dimension 3. Chaque neurone de sortie dispose de son propre vecteur de poids \(\mathbf{w_j}\) et de son biais scalaire \(b_j\). Remarquons que la couche intermédiaire, dite couche cachée, applique une fonction d’activation non-linéaire \(\phi\).

Il devient nécessaire de formaliser les notations. À partir du maintenant, nous noterons l’entrée \(\mathbf{x} \in \mathbb{R}^m\), la sortie du PMC \(\hat{\mathbf{y}} \in \mathbb{R}^k\) et la couche cachée \(\mathbf{h} \in \mathbb{R}^d\). On notera \(\mathbf{W}_e, \mathbf{b}_e\) la matrice de poids \((m, d)\) et le vecteur de biais reliant les entrées à la couche cachée, et \(\mathbf{W}_s, \mathbf{b}_s\) la matrice de poids \((d, k)\) et le vecteur de biais reliant la couche cachée aux sorties. Chaque couche s’obtient de la précédente par l’équation du perceptron

\[\mathbf{h} = \phi\left(\mathbf{W}_e \mathbf{x} + \mathbf{b}_e\right)~~,\]

et

\[\hat{\mathbf{y}} = \mathbf{W}_s \mathbf{h} + \mathbf{b}_s~~.\]

Il est possible d’appliquer une fonction d’activation sur la sortie \(\hat{\mathbf{y}}\), par exemple un softmax pour la classification.

Il est bien entendu possible de construire un perceptron multi-couche avec plus d’une couche cachée. Dans ce cas, on passe des activations cachée \(\mathbf{h}^{(l)}\) à la suivante \(\mathbf{h}^{(l)}\) par l’équation habituelle :

\[\mathbf{h}^{(l+1)} = \phi\left(\mathbf{W}^{(l)} \mathbf{h}^{(l)} + \mathbf{b}^{(l)}\right) ~~.\]

Non-linéarité

Il est important de noter que la non-linéarité de la fonction d’activation est essentielle à la construction des perceptrons multi-couche. En effet, considérons que la fonction d’activation choisie soit une fonction affine définie par \(\phi(x) = \alpha x + \beta\). En reprenant les équations d’un perceptron multi-couche à une couche cachée :

\[\mathbf{\hat{y}} = \phi(\mathbf{W}_s \mathbf{h} + \mathbf{b}_s) ~~~\text{et}~~~\mathbf{h} = \phi(\mathbf{W}_e \mathbf{x} + \mathbf{b}_e)\]

En composant les deux équations :

\[\mathbf{\hat{y}} = \phi\left(\mathbf{W}_s \phi(\mathbf{W}_e \mathbf{x} + \mathbf{b}_e) + \mathbf{b}_s \right)\]

En remplaçant par la définition de \(\phi\), il vient:

\[\mathbf{\hat{y}} = \phi\left(\mathbf{W}_s (\alpha \mathbf{W}_e \mathbf{x} + \alpha \mathbf{b}_e + \beta) + \mathbf{b}_s \right)\]

\[\mathbf{\hat{y}} = \alpha \mathbf{W}_s (\alpha \mathbf{W}_e \mathbf{x} + \alpha \mathbf{b}_e + \beta) + \mathbf{b}_s + \beta\]

\[\mathbf{\hat{y}} = \alpha^2 \mathbf{W}_s \mathbf{W}_e \mathbf{x} + \alpha^2 \mathbf{W}_s \mathbf{b}_e + \alpha \beta \mathbf{W}_s + \mathbf{b}_s + \beta\]

Ce qui est équivalent à un perceptron à une seule couche de matrice de poids \(\mathbf{W} = \alpha^2 \mathbf{W}_s \mathbf{W}_e\) et de biais \(\alpha^2 \mathbf{W}_s \mathbf{b}_e + \alpha \beta \mathbf{W}_s + \mathbf{b}_s + \beta\). Autrement dit, ajouter des couches au perceptron n’augmente pas l’expressivité du modèle si les fonctions d’activation ne sont pas non-linéaires.

Théorème d’approximation universelle

Une propriété intéressante des réseaux de neurones artificiels est leur capacité à approcher n’importe quelle fonction qui ne soit pas excessivement irrégulière. En effet, il existe un théorème dit d’approximation universelle portant sur les perceptrons multi-couche dont la fonction d’activation \(\phi\) est continue et non polynomiale.

Théorème [1Cyb89]

Soit \(f\) une fonction continue (sur des compacts) de \(\mathbb{R}^m\) vers \(\mathbb{R}^d\). Alors, pour tout réel \(\varepsilon > 0\), il existe un perceptron multi-couche à une seule couche cachée de nombre de neurones fini \(\hat{f} : x \in \mathbb{R}^m \rightarrow \mathbf{W}_s \phi(\mathbf{W}_e \cdot x + \mathbf{b}_e) + \mathbf{b}_s\) qui est une approximation de \(f\) à \(\varepsilon\) près, c’est-à-dire :

\[\max_{x \in \mathbb{R}^m} \left\lVert f(x) - \hat{f}(x)\right\rVert < \varepsilon\]

si la fonction d’activation \(\phi\) est non-polynomiale.

Autrement dit, quel que soit le problème de modélisation décisionnel auquel nous faisons face, du moment que la fonction mathématique sous-jacente est continue, alors il existe un réseau de neurones qui sera en mesure de l’approcher, quel que soit le degré de précision que l’on s’impose. Ce résultat a été démontré initialement par Cybenko en 1989 (pour les sigmoïdes) puis étendu à l’ensemble des percetrons multi-couche par Hornik en 1991. Il existe de nombreuses variantes de ce théorème. La version présentée ici est dite de largeur arbitraire (et de profondeur 1), mais il en existe d’autres pour la profondeur arbitraire, de largeur bornée, etc. Il faut toutefois noter deux limites à ce théorème:

• Un perceptron multi-couche à une seule couche cachée suffit à approcher n’importe quelle fonction continue. Cependant, le théorème ne donne aucune indication sur la dimensionalité de la couche cachée. Autrement dit, le nombre de neurones (et donc de paramètres) dans le modèle n’est pas borné ! Peut-être que le PMC idéal nécessite des centaines de milliards de paramètres.

• La démonstration du théorème d’approximation universelle prouve l”existence d’un PMC approchant la fonction désirée à une précisoin arbitraire. Toutefois, elle ne donne aucune méthode pour déterminer les paramètres \(\mathbf{W}\) et \(\mathbf{b}\) de ce modèle. Il n’y a aucune garantie que les algorithmes d’optimisation que nous allons utiliser par la suite permettent de trouver ce modèle idéal.

Ce théorème est donc un résultat théorique. Il garantit, en principe, que les perceptrons multi-couches peuvent être utilisés pour approcher de nombreuses fonctions. Pour autant, il ne donne aucune indication sur comment les mettre en œuvre en pratique.

Rétropropagation

Descente de gradient

La descente de gradient est un algorithme d’optimisation permettant de déterminer un minimum d’une fonction différentiable. Cet algorithme va nous être particulièrement utile pour l’apprentissage des réseaux de neurones. En effet, jusqu’à présent nous avons vu la construction des perceptrons multi-couches mais nous n’avons pas encore de méthode nous permettant de déterminer leurs paramètres, c’est-à-dire les poids (et biais) des différentes couches. Nous allons utiliser pour cela l’algorithme du gradient.

Cas univarié

Commençons par rappeler le fonctionnement de la descente de gradient. Considérons le cas en dimension 1, c’est-à-dire pour une fonction \(f: \mathbb{R} \rightarrow \mathbb{R}\) univariée. On cherche à déterminer le point \(x \in \mathbb{R}\) tel que \(f(x)\) soit minimal, c’est-à-dire que \(x\) est un minimum pour la fonction \(f\). Prenons un exemple avec la fonction \(f(x) = x^2\). Pour initialiser l’algorithme, nous devons d’abord choisir un point de départ. Prenons, arbitrairement, \(x_0 = 2.8\). Dans quelle direction peut se trouver le minimum de la fonction \(f\) ? En observant la dérivée de \(f\) (ici, \(f'(x) = 2x\)), on s’aperçoit qu’autour du point \(x_0\), la fonction est croissante \(x\) quand et donc décroît lorsque \(x\) diminue. Nous devons donc déplacer \(x\) vers la gauche et répéter l’opération avec le nouveau point. Pour savoir quand s’arrêter, il suffit d’observer la valeur de la dérivée : la dérivée s’annule sur extremum local. Si \(f'(x) = 0\), alors nous sommes sur un minimum (ou un maximum) local.

L’algorithme est donc le suivant.

1. Définir un point de départ \(x_0\).

2. Calculer \(f'(x_k)\). Si \(f'(x_k) < \varepsilon\), alors s’arrêter.

3. Mettre à jour en se déplaçant dans la direction opposée à la dérivée (descendre la pente): \(x_{k+1} = x_k - \alpha f'(x_k)\)

4. Répéter tant que le critère d’arrêt n’est pas atteint.

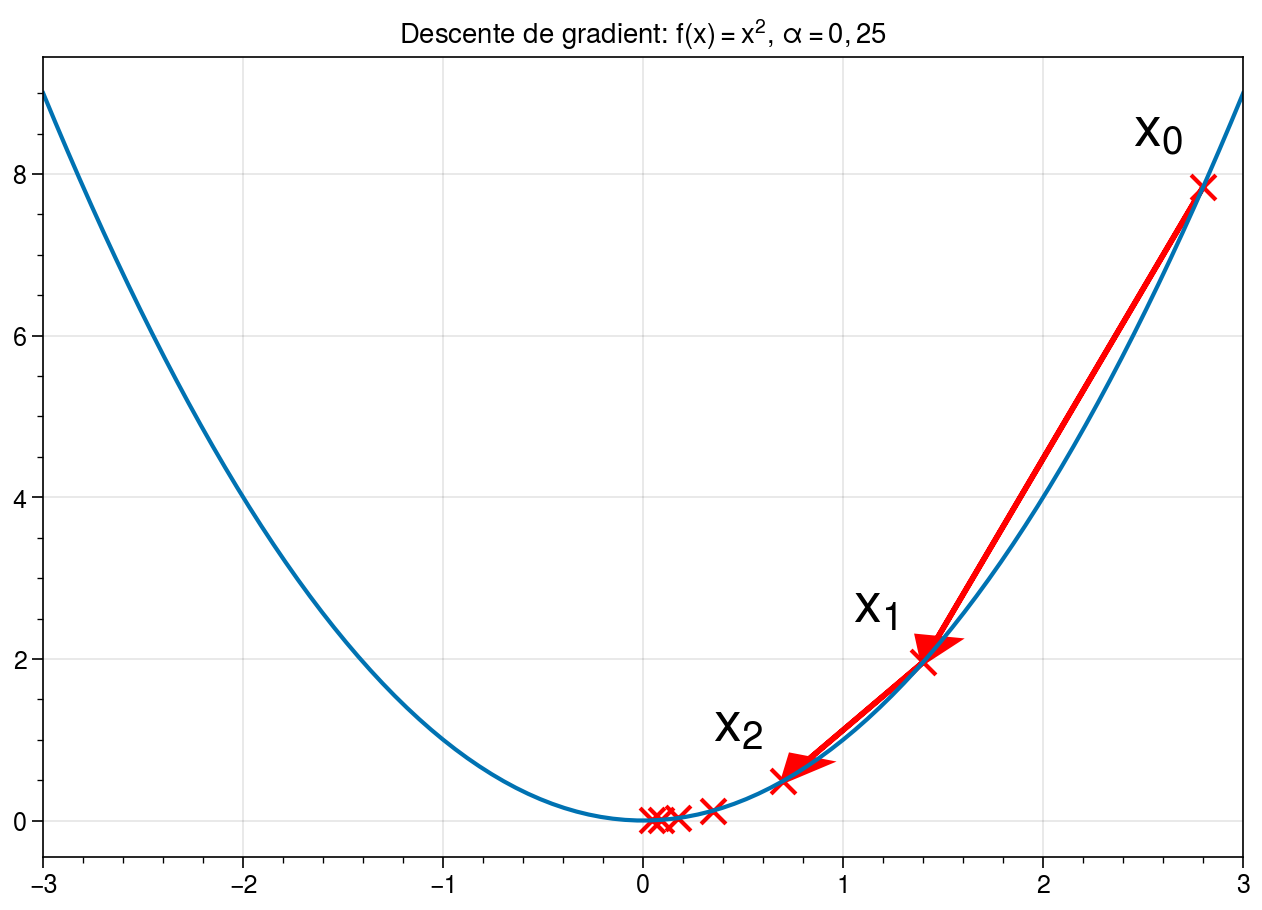
En partant du point \(x_0 = 2.8\), nous pouvons nous déplacer vers \(x_1\), puis \(x_2\) et ainsi de suite. La descente de gradient converge vers le minimum en zéro de la fonction quadratique. Chaque déplacement est plus faible que le précédent puisque la dérivée diminue à mesure que l’on s’approche de zéro.

L’algorithme nécessite donc de définir deux paramètres: \(\varepsilon > 0\) qui représente la tolérence de l’algorithme (en-dessous de quel seuil considère-t-on que la dérivée est nulle ?) et \(\alpha\) qui représente l’amplitude du déplacement selon la pente de la dérivée. Plus \(\alpha\) est faible, plus les déplacements sont petits. La convergence peut donc prendre de nombreuses itérations. Mais si \(\alpha\) est trop élevé, il est aussi possible que le déplacement nous fasse « sauter » le minimum, provoquant des oscillations!

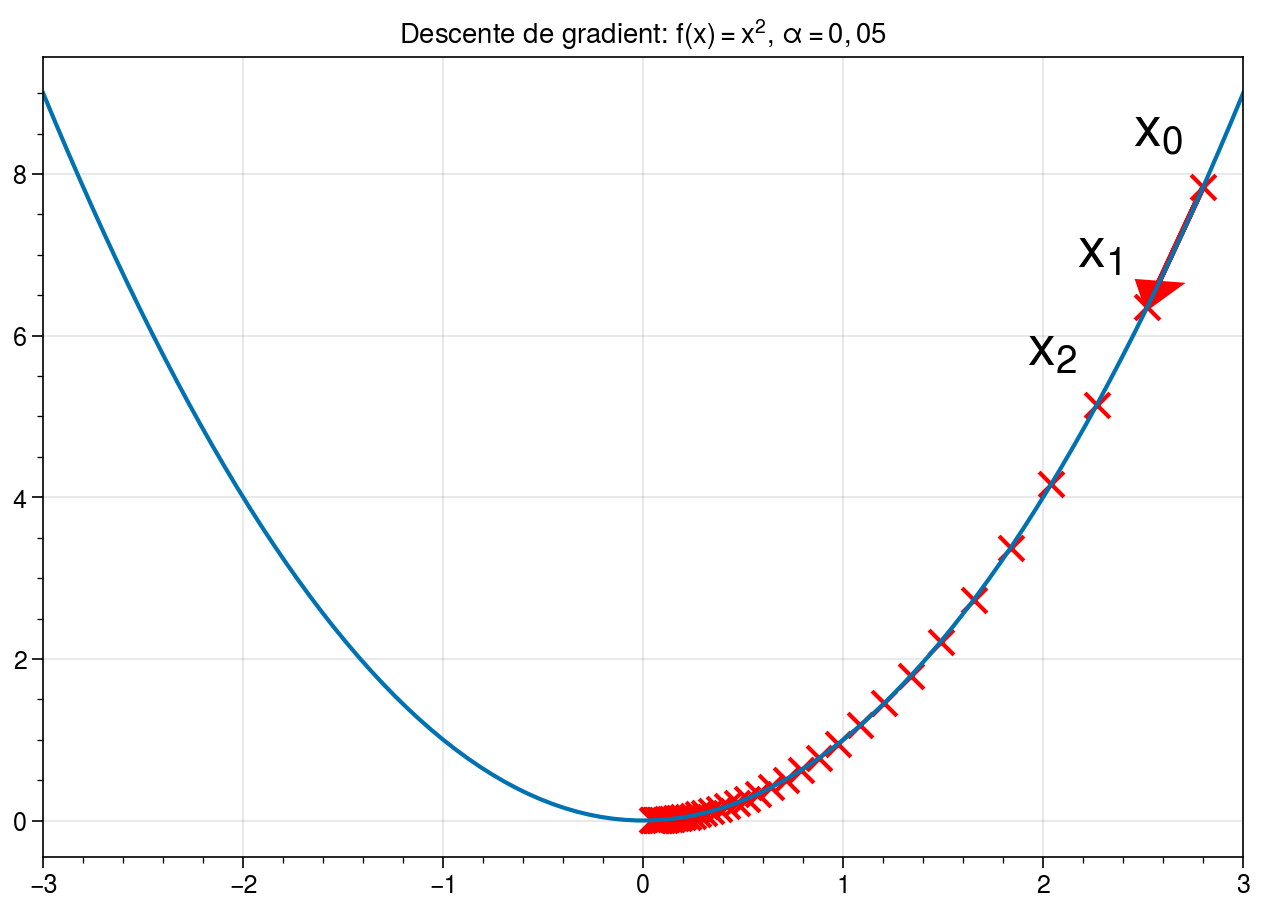
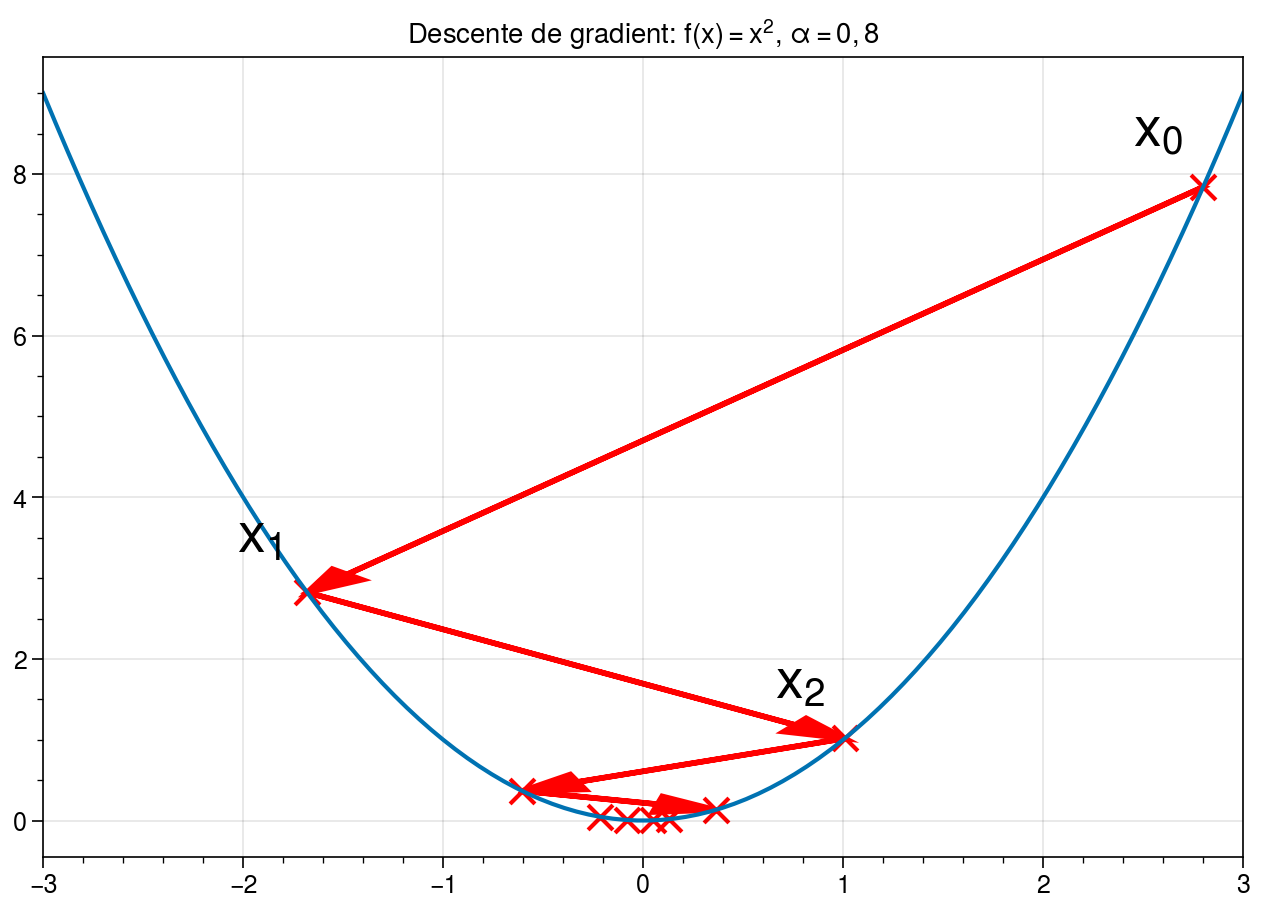
Par ailleurs, il est important de remarquer que la convergence de l’algorithme n’est pas garantie. En effet, l’exemple précédent est un cas particulièrement favorable pour la descente de gradient car la fonction \(f: x \rightarrow x^2\) est une fonction convexe. Dans ce cas, l’algorithme du gradient est garanti de converger et le minimum obtenu est un minimum global. En pratique, nous ne manipulerons pas des fonctions convexes. La convergence ne pourra donc se faire qu’au mieux sur des minima locaux.

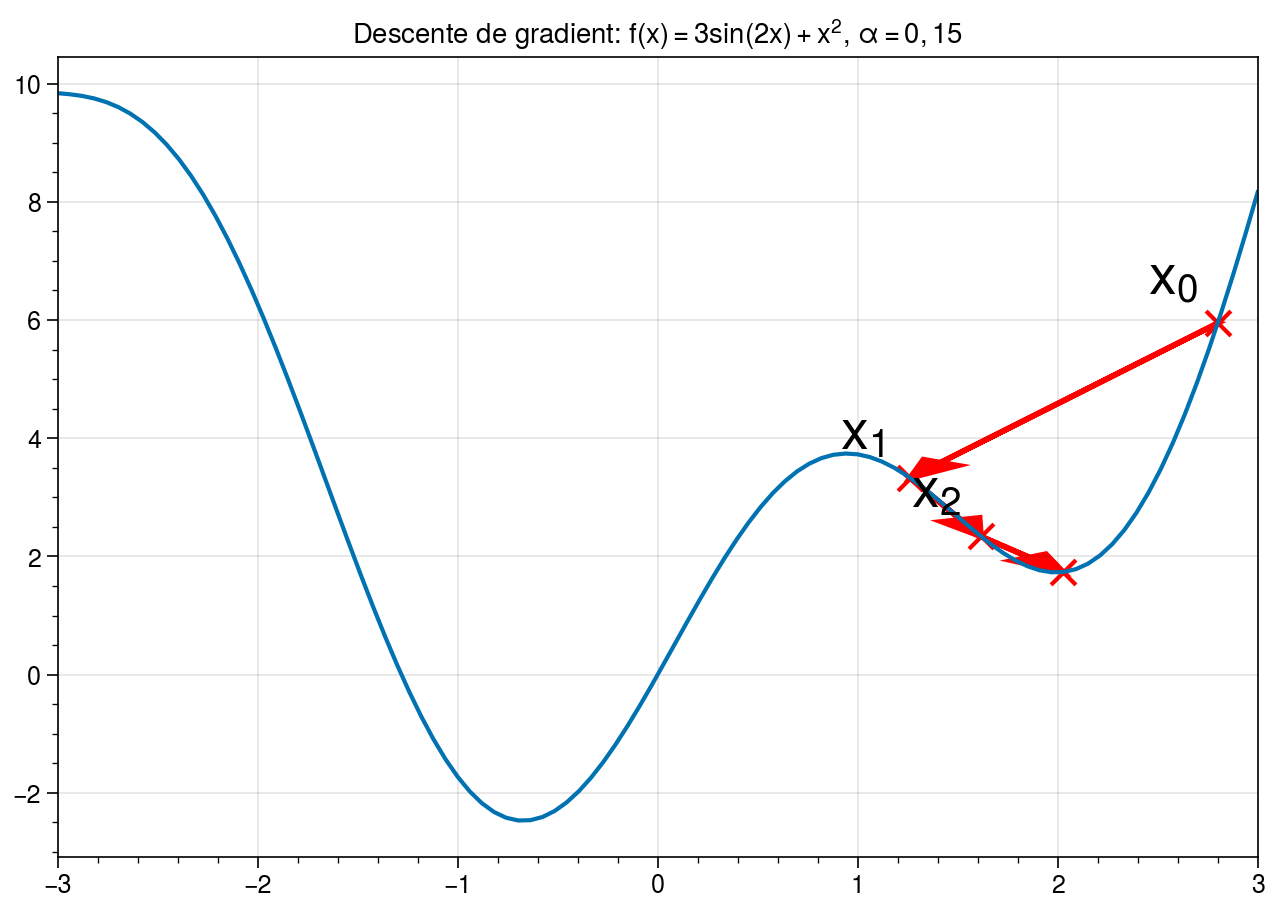
Lorsque la fonction à optimiser n’est pas convexe, la convergence de l’algorithme vers un minimum global n’est pas garantie. En fonction de l’optimisation, il est possible d’atteindre un minimum local moins bon que le minimum global.

Cas multivarié

Dans le cas général, les fonctions que nous manipulons sont multivariées, c’est-à-dire à plusieurs variables: \(f: (x_1, x_2, \dots, x_n) \in \mathbb{R}^n \rightarrow \mathbb{R}\). L’algorithme du gradient s’applique encore à condition que la fonction \(f\) soit différentiable. La plus forte pente est alors définie par la direction du gradient de \(f\), noté \(\overrightarrow{\nabla} f\). En un point \(a \in \mathbb{R}^n\), le gradient de \(f\) est égal au vecteur des dérivées partielles selon chaque composante:

\[\overrightarrow{\nabla} f(a) = \begin{pmatrix} \frac{\partial f}{\partial x_1}(a) \\ \frac{\partial f}{\partial x_2}(a) \\ \vdots \\ \frac{\partial f}{\partial x_n}(a) \end{pmatrix}\]

Le gradient est donc un vecteur même si la flèche sera omise par la suite pour simplifier la lecture. L’algorithme du gradient précédent vu se réécrit donc de la façon suivante :

1. Définir un point de départ \(x_0\).

2. Calculer \(f'(x_k)\). Si la norme du gradient est inférieure au seuil \(\lVert f'(x_k) \rVert < \varepsilon\), alors s’arrêter.

3. Mettre à jour en se déplaçant dans la direction opposée à la dérivée (descendre la pente): \(x_{k+1} = x_k - \alpha f'(x_k)\)

4. Répéter tant que le critère d’arrêt n’est pas atteint.

Comme nous n’avons pas de garantie de convergence dans le cas général, le critère d’arrêt pourra également consister en un nombre d’itérations maximal à ne pas dépasser.

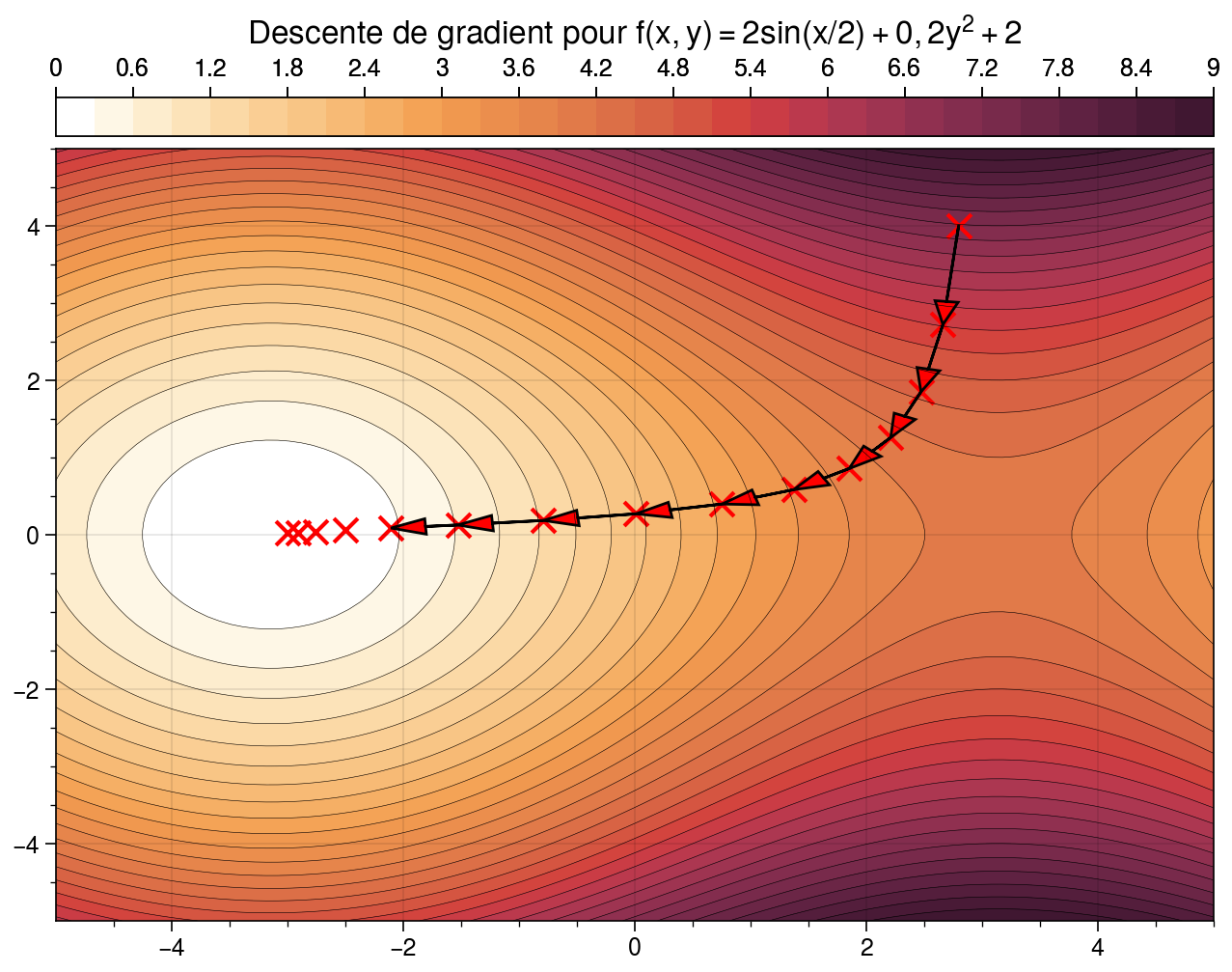
En partant du point \(x_0 = (2.8; 4)\), la descente de gradient calcule la direction de plus forte pente (indiquée ici par les flèches) et applique l’algorithme d’optimisation iérative. La surface présente ici un minimum local bien identifié autour de \((0; -3.14)\) vers lequel l’optimisation converge.

Dans le cas multivarié, la descente de gradient permet de déterminer des points stationnaires, c’est-à-dire des points auxquels le gradient s’annule. Ces points ne sont pas nécessairement des minima locaux, il peut également s’agir de points selles. Toutefois, nous verrons que cela ne pose pas de problème en pratique pour l’entraînement des réseaux de neurones.

Optimisation du perceptron multi-couche

Revenons aux perceptrons multi-couches. Dans notre cas, nous disposons d’un modèle dont les paramètres \(\mathbf{W}\) sont à déterminer. Pour ce faire, nous allons minimiser une fonction de coût. Cette fonction de coût mesure l’erreur commise en effectuant une prédiction \(\hat{y}\) plutôt que la variable à prédire réelle \(y^*\). Dans le cas de la régression, il peut par exemple s’agir de l’erreur quadratique moyenne (distance \(L_2\)) \(\mathcal{L} = \lVert \hat{y} - y^* \rVert^2\). Toutefois, nous allons pour l’instant nous concentrer sur la classification. La variable à prédire \(y^*\) est une variable catégorielle discrète sous forme d’encodage one-hot: \(y^* = (0, 0, \dots, 1 \dots, 0)\). En sortie du perceptron multi-couche, nous obtenons un vecteur \(\hat{y}\) comprenant autant de composantes que de classes à prédire. Ce vecteur est passé dans une activation softmax. Si la classe à prédire est la classe \(j\), l’objectif est donc que la composante \(\hat{y}_i\) soit nulle si \(i \neq j\) et soit égale à 1 si \(i = j\). La fonction de coût utilisée sera l’entropie croisée:

\[\mathcal{L}(\hat{y}, y^*) = - \sum_{i=1}^k y^*_i \log \hat{y}_i\]

L’entropie croisée est un cas particulier de la divergence de Kullback-Leibler. Cette dernière est une mesure de dissimilarité entre deux distributions de probabilités. Ce n’est pas une distance au sens strict, car elle ne vérifie pas l’ingéalité triangulaire et qu’elle n’est pas symétrique. La divergence de Kullback-Leibler, ou divergence KL, de la distributions de probabilité discrète \(P\) par rapport à \(Q\) sur un ensemble \(X\) s’écrit :

\[\mathcal{D}_\text{KL}(P | Q) = \sum_{x \in X} P(x) \log \frac{P(x)}{Q(x)}\]

Dans notre cas, \(P\) et \(Q\) sont des histogrammes avec \(P(i)\) la probabilité de la i-ème classe de sortie, c’est-à-dire \(\hat{y}_i\), et \(Q(i)\) la probabilité que la classe \(i\) soit la bonne selon la vérité terrain, c’est-à-dire \(y^*_i\) (qui vaut 0 pour toutes les classes, sauf pour la classe qui est correcte). Une proprieté intéressante de la divergence de Kullback-Leibler est que, si \(\mathcal{D}_\text{KL}(P|Q) = 0\), alors les distributions \(P\) et \(Q\) sont égales (cf. par exemple cette preuve utilisant l’inégalité de Jensen). En minimisant la divergence KL, on peut alors rapprocher la distribution \(P\) de la distribution \(Q\). Dans notre cas, nous allons donc chercher à modifier les paramètres \(\mathbf{W}\) du modèle, de sorte à minimiser la divergence de Kullback-Leibler entre \(\hat{y}\) et \(y^*\), c’est-à-dire leur entropie croisée.

À noter que pour d’autres problèmes, il est possible d’utiliser d’autres fonctions de coût. Les seuls critères sont :

• que minimiser la fonction de coût fasse tendre les prédictions du modèle vers la vérité terrain,

• que la fonction de coût soit différentiable par rapport aux paramètres du modèle.

Pour des problèmes de régression, on utilisera par exemple l’erreur quadratique moyenne \(\lVert \hat{y} - y^* \rVert\) ou l’erreur absolue \(| \hat{y} - y^* |\), qui respectent ces deux propriétés.

Quelque soit la fonction de coût choisie, nous allons la minimiser en appliquant l’algorithme de descente de gradient sur \(\mathcal{L}\) et les poids \(\mathbf{W}\) du modèle. En effet, puisque les prédictions \(\hat{y}_i\) dépendent du modèle, en réalité la fonction \(\mathcal{L}\) est une fonction des entrées \(\mathbf{x}\), de la vérité terrain \(\mathbf{y}^*\) et des paramètres \(\mathbf{W}\) du perceptron. Il nous faut donc calculer les gradients \(\nabla \mathbf{W}\) afin de savoir comment réaliser l’étape de mise à jour de l’algorithme de descente de gradient.

Descente de gradient stochastique

Les fonctions de coût que l’on utilise permettent de calculer l’erreur commise par le modèle sur une observation. Pour un jeu de données \(\mathcal{D} = \{(\mathbf{x}^1, y^1), (\mathbf{x}^2, y^2), \dots, (\mathbf{x}^N, y^N\}\), on s’intéressera alors à l’erreur empirique sur l’intégralité du jeu d’apprentissage :

\[\mathcal{L}(\mathcal{D}; \mathbf{W}) = \frac{1}{N} \sum_{i=1}^N \mathcal{L}(\hat{y}^i, y^{*,i};\mathbf{W})\]

Le calcul de l’erreur empirique requiert néanmoins de calculer la prédiction \(\hat{y}^i\) pour tous les exemples du jeu d’apprentissage, avant même de pouvoir considérer calculer son gradient par rapport aux paramètres du modèle \(\mathbf{W}\). Une itération de la descente de gradient nécessite donc une passe complète sur le jeu de données d’apprentissage, ce qui est en général coûteux lorsque le nombre d’exemples \(N\) est grand. À la place, il est courant d’utiliser l’algorithme de descente de gradient stochastique. Cet algorithme consiste à remplacer l’erreur empirique réelle par l’erreur sur un seul exemple \(\mathcal{L}^i = \mathcal{L}(\hat{y}^i, y^{*,i}; \mathbf{W})\). Toutefois, cette approximation a tendance à ralentir la convergence de la descente de gradient, car deux observations \(\mathbf{x}^i\) et \(\mathbf{x}^j\) différentes peuvent avoir des erreurs différentes et donc des gradients pointant dans des directions différentes, introduisant des oscillations. Afin de lisser cette estimation du gradient, l’algorithme utilisé est une descente de gradient par mini-batch (en français par « lot », plus communément simplement par batch). À chaque itération de la descente de gradient, on tire aléatoirement un batch de \(k\) exemples \(\{\mathbf{x}^{i_1}, \dots, \mathbf{x}^{i_k}\}\) uniformément parmi l’ensemble d’apprentissage \(\mathcal{D}\). L’erreur d’apprentissage est alors calculée sur les exemples du batch :

\[\mathcal{L}(\text{batch}; \mathbf{W}) = \frac{1}{k} \sum_{j = i_1}^{i_k} \mathcal{L}(\hat{y}^{j}, y^{*,j};\mathbf{W})\]

Plus \(k\) est grand, plus une itération nécessite de calculs, mais plus l’estimation de l’erreur se rapproche de l’erreur totale sur le jeu d’entraînement. En pratique, l’utilisation de processeurs de calculs parallèles permet de calculer plusieurs prédictions \(\hat{y}^i\) en parallèle, ce qui permet d’utiliser la descente de gradient stochastique par batch avec une augmentation négligeable des temps de calcul.

Calcul des gradients

Pour réaliser l’optimisation à proprement parler, nous devons maintenant calculer le terme de mise à jour des paramètres dans l’algorithme de descente de gradient. Il s’agit des gradients \(\nabla_\mathbf{W} \mathcal{L}(\hat{y}, y^* ; \mathbf{W})\) de la fonction de coût par rapport aux paramètres du modèle. Pour obtenir ces gradients, nous utiliser l’algorithme de rétropropagation (ou backpropagation), introduit par Linnainmaa et popularisé par Werbos et Rumelhart et al. dans les années 80 pour les réseaux de neurones. Cet algorithme consiste à utiliser le théorème de dérivation des fonctions composées, ou chain rule (dérivées en chaîne), de sorte à calculer les gradients des poids des couches intermédiaires à partir des gradients de leur sortie. Schématiquement, il s’agit ainsi d’effectuer la décomposition suivante :

\[\frac{\partial \mathcal{L}}{\partial \mathbf{W}} = \underbrace{\frac{\partial \mathcal{L}}{\partial \hat{y}}}_\text{étape 1} \underbrace{\frac{\partial \hat{y}}{\partial \mathbf{h}}}_\text{étape 2} \underbrace{\frac{\partial \mathbf{h}}{\partial \mathbf{W}}}_\text{étape 3}\]

Considérons une entrée \(\mathbf{x_i} \in \mathbb{R}^d\). On note \(\hat{\mathbf{y_i}} = (y_{1,i}, y_{2,i}, \dots, y_{K, i})\) le vecteur des prédictions (\(K\) classes) et \(\mathbf{y_i^*}\) le vecteur de la vérité terrain pour l’example \(\mathbf{x_i}\).

Dans le cas d’un problème de classification optimisé par l’entropie croisée, on rappelle que :

\[l_\text{CE}(\hat{\mathbf{y_i}}, \mathbf{y_i}^*) = - \sum_{c'=1}^K y^*_{c',i} \log(\hat{y}_{c',i})\]

\[\hat{y}_{c,i} = \operatorname{softmax}(s_{c,i}) = \frac{\exp(s_{c,i})}{\sum_{c'=1}^K \exp(s_{c',i})}\]

\[\mathbf{s_i} = \mathbf{W} \mathbf{h} + \mathbf{b}\]

• Dans le cas de la régression logistique : \(\mathbf{h} = \mathbf{x_i}\) (pas de couche cachée).

• Dans le cas du perceptron multi-couche : \(\mathbf {h} = \sigma(\mathbf{W^h} \mathbf{x_i} + \mathbf{b^h})\) (une couche cachée).

Étape 1 : \(\nabla_\mathbf{\hat{y_i}} l_\text{CE}\)

Pour commencer, nous allons calculer la dérivée partielle de l’entropie croisée, c’est-à-dire du coût \(l_\text{CE}\), par rapport à la \(c\)-ième composant \(\hat{y}_{c,i}\) du vecteur de prédictions :

\[\begin{align} \frac{\partial l_\text{CE}}{\partial \hat{y_{c,i}}} &= \frac{\partial}{\partial \hat{y_{c,i}}}\left( - \sum_{c'=1}^K y^{*}_{c',i} \log (\hat{y_{c',i}}) \right)\\ &= -\sum_{c'=1}^K \frac{\partial}{\partial \hat{y_\text{c,i}}} \left(y^{*}_{c',i} \log (\hat{y_{c',i}})\right)\\ \end{align}\]

Soit \(c^*\) la classe de la vérité terrain (c’est-à-dire la vraie classe de \(\mathbf{x_i}\). Alors \(y^*_\text{c*, i} = 1\) et \(y^*_\text{c', i} = 0\) pour \(c' \neq c^*\). Les termes de la somme de l’équation précédente sont tous nuls à l’exception du cas \(c' = c^*\) :

\[\begin{align} \frac{\partial l_\text{CE}}{\partial \hat{y_{c,i}}} &= - \frac{\partial}{\partial \hat{y_{c,i}}} (y_{c^*,i} \log (\hat{y}_{c^*,i})) &= - \frac{\partial}{\partial \hat{y_{c,i}}} \log (\hat{y}_{c^*,i}) ~~~~\text{car}~~~~ y_{c^*,i} = 1\\ \end{align}\]

Donc pour tout \(c \neq c^*, \frac{\partial l_\text{CE}}{\partial \hat{y_{c,i}}} = 0\). Dans le cas \(c = c^*\), alors :

\[\frac{\partial l_\text{CE}}{\partial \hat{y_{c^*,i}}} = - \frac{\partial \log{\hat{y}_{c^*,i }}}{\partial \hat{y_{c^*,i}}} = - \frac{1}{\hat{y}_{c^*,i }}\]

Autrement dit, le gradient s’écrit :

\[\nabla_{\mathbf{\hat{y}_i}} l_\text{CE} = (0, \dots, \underbrace{\frac{-1}{\hat{y}_{c^*, i}}}_{\text{composante}~ c^*} , \dots, 0)^T\]

ce qui peut se réécrire comme la multiplication élément par élément (\(\odot\)) entre \(\frac{1}{\hat{y}_{c^*,i}}\) et un vecteur binaire \(\delta_{c, c^*}\):

\[\nabla_{\mathbf{\hat{y}_i}} l_\text{CE} = \frac{-1}{\hat{y}_{c^*, i}} \odot (0, \dots, \underbrace{1}_{\text{composante}~ c^*} , \dots, 0)^T = \frac{-1}{\hat{y}_{c^*, i}} \odot \mathbf{\delta_{c,c^*}}\]

Étape 2 : \(\nabla_\mathbf{s_i} l_\text{CE}\)

Par chain rule (théorème de dérivation des fonctions composées), on a l’égalité :

\[\frac{\partial l_\text{CE}}{\mathbf{s_i}} = \frac{\partial l_\text{CE}}{\partial \mathbf{\hat{y_i}}} \frac{\partial \mathbf{\hat{y_i}}}{\partial \mathbf{s_i}}\]

Pour calculer les gradients de l’entropie croisée par rapport aux activations avant softmax (logits), on doit donc calculer tous les coefficients \(\frac{\partial {\hat{y_{p,i}}}}{\partial {s_{q,i}}}\) de la matrice Jacobienne :

\[\frac{\partial \hat{y_{p,i}}}{\partial s_{q,i}} = \frac{\partial~\text{softmax}(s_{p,i})}{\partial s_{q,i}} = \frac{\partial \left(\frac{\exp(s_{p,i})}{\sum_{p'=1}^K \exp(s_{p',i})}\right)}{\partial s_{q,i}}\]

Par le théorème de dérivation du quotient de deux fonctions (\((\frac{u}{v})' = \frac{uv' - u'v}{v^2}\)):

\[\begin{align} \frac{\partial \hat{y_{p,i}}}{\partial s_{q,i}} &= \frac{\frac{\partial}{\partial s_{q,i}} \left(\exp(s_{p,i})\right)\sum_{p'=1}^K \exp(s_{p',i}) - \exp(s_{p,i}) \frac{\partial}{\partial s_{q,i} } \left(\sum_{p'=1}^K \exp(s_{p',i})\right)}{\left(\sum_{p'=1}^K \exp(s_{p',i})\right)^2}\\ \end{align}\]

Il faut distinguer deux cas :

\[\frac{\partial}{\partial s_{q,i}} \exp(s_{p,i}) = \begin{cases} 0 & \text{si} & p\neq q\\ \exp(s_{p,i}) & \text{si} & p = q\\ \end{cases}\]

Pour cette raison, la dérivation de la somme au numérateur donne dans tous les cas :

\[\frac{\partial}{\partial s_{q,i} } \left(\sum_{p'=1}^K \exp(s_{p',i})\right) = \sum_{p'=1}^K \frac{\partial}{\partial s_{q,i} } \exp(s_{p',i}) = \exp(s_{q,i})\]

donc la dérivée partielle se réécrit :

\[\begin{align} \frac{\partial \hat{y_{p,i}}}{\partial s_{q,i}} &= \frac{\frac{\partial}{\partial s_{q,i}} \left(\exp(s_{p,i})\right)\sum_{p'=1}^K \exp(s_{p',i}) - \exp(s_{p,i}) \exp(s_{q,i})}{\left(\sum_{p'=1}^K \exp(s_{p',i})\right)^2}\\ \end{align}\]

Cas \(p = q\) :

On remplace \(q\) par \(p\) dans l’équation précédente, partout au numérateur :

\[\def\S{\sum_{p'=1}^K \exp(s_{p',i})} \begin{align} \frac{\partial \hat{y_{p,i}}}{\partial s_{p,i}} &= \frac{\underbrace{\frac{\partial}{\partial s_{p,i}} \left(\exp(s_{p,i})\right)}_\text{dérivée de $\exp$}\sum_{p'=1}^K \exp(s_{p',i}) - \exp(s_{p,i}) \exp(s_{p,i})}{\left(\sum_{p'=1}^K \exp(s_{p',i})\right)^2}\\ &= \frac{\exp(s_{p,i}) \S - \exp(s_{p,i}) \exp(s_{p,i})}{(\sum_{p'=1}^K \exp(s_{p',i}))^2}\\ &= \frac{\exp(s_{p,i})\left(\S - \exp(s_{p,i})\right)}{(\sum_{p'=1}^K \exp(s_{p',i}))^2}\\ &= \underbrace{\frac{\exp(s_{p,i})}{\S}}_\text{softmax de $s_{p,i}$} \cdot \frac{\sum_{p'=1}^K \exp(s_{p',i}) - \exp(s_{p,i})}{\S}\\ &= \hat{y}_{p,i} \cdot (1 - \underbrace{\frac{\exp(s_{p,i})}{\sum_{p'=1}^K \exp(s_{p',i})}}_{\text{softmax de } s_{p,i}})\\ &= \hat{y}_{p,i} \cdot (1 - \hat{y}_{p,i}) \end{align}\]

Cas \(p \neq q\) :

\[\def\S{\sum_{p'=1}^K \exp(s_{p',i})} \begin{align} \frac{\partial \hat{y_{p,i}}}{\partial s_{q,i}} &= \frac{\underbrace{\frac{\partial}{\partial s_{q,i}} \left(\exp(s_{p,i})\right)}_{0 \text{ car } p \neq q} \sum_{p'=1}^K \exp(s_{p',i}) - \exp(s_{p,i}) \exp(s_{q,i})}{\left(\sum_{p'=1}^K \exp(s_{p',i})\right)^2}\\ &= \frac{0 - \exp{s_{p,i} \exp{s_{q,i}}}}{(\sum_{p'=1}^K \exp(s_{p',i}))^2}\\ &= -\underbrace{\frac{\exp(s_{p,i})}{\sum_{p'=1}^K \exp(s_{p',i})}}_\text{softmax de $s_{p,i}$} \cdot \underbrace{\frac{\exp(s_{q,i})}{\S}}_\text{softmax de $s_{q,i}$}\\ &= - \hat{y_{p, i}} \; \hat{y_{q, i}} \end{align}\]

Cas général

Notons \(\delta_{p,q}\) le delta de Kroneker qui vaut 1 si \(p=q\) et 0 sinon :

\[\delta_{p,q} = \begin{cases} 1 ~~~p = q \\ 0 ~~~p \neq q \end{cases}\]

En combinant les deux cas précédents, il vient finalement :

\[\frac{\partial \hat{y_{p,i}}}{\partial s_{q,i}} = \hat{y}_{p,i} (\delta_{p,q} - \hat{y}_{q,i})\]

Le gradient qui nous intéresse \(\nabla_\mathbf{s_i} l_\text{CE}\) s’obtient finalement par le produit du gradient \(\nabla_\mathbf{\hat{y}_i} l_\text{CE}\) calculé à l’étape 1 et de la matrice jacobienne calculé à l’étape 2.

On rappelle que le gradient vaut :

\[\nabla_\mathbf{\hat{y}_i} l_\text{CE} = \left(0, 0, \dots, \underbrace{\frac{-1}{\hat{y}_{c^*, i}}}_{c^*}, \dots, 0 \right)^T\]

et que la matrice jacobienne calculée précédemment s’écrit :

\[J_\mathbf{\hat{y}_i}(\mathbf{s}_i) = \begin{pmatrix}{ \dfrac {\partial \hat{y}_{1,i}}{\partial s_{1, i}}} & \cdots &{\dfrac {\partial \hat{y}_{1, i}}{\partial s_{k, i}}}\\ \vdots & \ddots & \vdots \\ {\dfrac {\partial \hat{y}_{k, i}}{\partial s_{1, i}}} & \cdots & {\dfrac {\partial y_{k, i}}{\partial s_{k, i}}} \end{pmatrix} = \begin{pmatrix}{ \hat{y}_{1,i} (1 - \hat{y}_{1,i})} & \cdots & {- \hat{y}_{1,i} \hat{y}_{k,i}}\\ \vdots & \ddots & \vdots \\ {- \hat{y}_{k,i} \hat{y}_{1,i}} & \cdots & {\hat{y}_{k,i} (1 - \hat{y}_{k,i})} \end{pmatrix}\]

Le gradient par rapport aux activations \(\mathbf{s_i}\) s’écrit donc :

\[\nabla_\mathbf{s_i} l_\text{CE} = J_\mathbf{\hat{y}_i}(\mathbf{s}_i) \nabla_\mathbf{\hat{y}_i} l_\text{CE} = \begin{pmatrix}{ \hat{y}_{1,i} (1 - \hat{y}_{1,i})} & \cdots & {- \hat{y}_{1,i} \hat{y}_{k,i}}\\ \vdots & \ddots & \vdots \\ {- \hat{y}_{k,i} \hat{y}_{1,i}} & \cdots & {\hat{y}_{k,i} (1 - \hat{y}_{k,i})} \end{pmatrix} \begin{pmatrix} 0\\ \vdots\\ \frac{-1}{\hat{y}_{c^*, i}}\\ \vdots\\ 0 \end{pmatrix}\]

Comme toutes les composantes du vecteur sont nulles, sauf la \(c^*\)-ième, cela revient à sélectionner la colonne d’indice \(c^*\) de la matrice jacobienne :

\[\nabla_\mathbf{s_i} l_\text{CE} = \frac{-1}{\hat{y}_{c^*, i}} \begin{pmatrix} - \hat{y}_{1, i} \hat{y}_{c^*, i}\\ \vdots\\ \hat{y}_{c^*, i} (1 - \hat{y}_{c^*, i})\\ \vdots\\ - \hat{y}_{k, i} \hat{y}_{c^*, i} \end{pmatrix} = - \begin{pmatrix} - \hat{y}_{1, i}\\ \vdots\\ 1 - \hat{y}_{c^*, i}\\ \vdots\\ - \hat{y}_{k, i} \end{pmatrix} = - \underbrace{\begin{pmatrix} \hat{y}_{1, i}\\ \vdots\\ \hat{y}_{c^*, i}\\ \vdots\\ \hat{y}_{k, i} \end{pmatrix}}_{\mathbf{\hat{y}_i}} - \underbrace{ \begin{pmatrix} 0\\ \vdots\\ 1\\ \vdots\\ 0 \end{pmatrix}}_{\mathbf{y_i}^*} = \mathbf{\hat{y}_i} - \mathbf{y_i}^*\]

On note cette quantité \(\delta_i = \mathbf{\hat{y}_i} - \mathbf{y_i}^*\).

Étape 3 : \(\frac{\partial \mathbf{s_i}}{\partial \mathbf{W}}\)

Par chain rule toujours, il nous suffit d’avoir la matrice jacobienne de dimension \((K, LK)\) où \(L \times K\) est le nombre de paramètres de la matrice \(W\) de la couche cachée :

\[\frac{\partial \mathbf{s_i}}{\partial W} = \begin{pmatrix} \frac{\partial s_{i,1}}{\partial W_{1,1}} & \cdots & \frac{\partial s_{i,1}}{\partial W_{L,K}}\\ \vdots & \ddots & \vdots\\ \frac{\partial s_{i,K}}{\partial W_{1,1}} & \cdots & \frac{\partial s_{i,K}}{\partial W_{L,K}}\\ \end{pmatrix}\]

\[\frac{\partial s_{i,m}}{\partial W_{n,o}} = \frac{\partial}{\partial W_{n,o}} \left( h_i \underbrace{W_{.,m}}_{\text{colonne}~m} + b_{m}\right) = \frac{\partial}{\partial W_{n,o}} \left(\sum_{p=1}^L h_{i,p} W_{p,m} + b_{m}\right) = \begin{cases} h_{i,n} & \text{si}~o = m\\ 0 & \text{sinon}\\ \end{cases}\]

Étape 4 : tout ensemble

\[\frac{\partial l_i}{\partial W} = \begin{pmatrix} \frac{\partial l_i}{\partial W_{1, 1}} & \cdots & \frac{\partial l_i}{\partial W_{1, K}}\\ \vdots & \ddots & \vdots\\ \frac{\partial l_i}{\partial W_{L, 1}} & \cdots & \frac{\partial l_i}{\partial W_{L, K}}\\ \end{pmatrix}\]

Par chain rule :

\[\frac{\partial l_i}{\partial W_{l,k}} = \frac{\partial{l_i}}{\partial \mathbf{s_{i}}_{,k'}} \frac{\partial \mathbf{s_{i}}_{,k'}}{\partial W_{l,k}} = (\mathbf{y_i}_{,k'} - \mathbf{y_i}_{,k'}^*) \frac{\partial \mathbf{s_i}_{,k'}}{\partial W_{l,k}} = \begin{cases} (\mathbf{y_i}_{,k} - \mathbf{y_i}_{,k}^*) h_{i,l} & \text{si } k = k'\\ 0 & \text{sinon} \end{cases}\]

Donc :

\[\frac{\partial l_i}{\partial W} = \begin{pmatrix} \delta_{i,1} h_{i,1} & \cdots & \delta_{i,K} h_{i,1}\\ \vdots & \ddots & \vdots\\ \delta_{i,1} h_{i,L} & \cdots & \delta_{i,K} h_{i,L}\\ \end{pmatrix} = \delta_i h_i^T = \begin{pmatrix} \mathbf{y_i}_{,1} - \mathbf{y_i}_{,1}^*\\ \vdots\\ \mathbf{y_i}_{,K} - \mathbf{y_i}_{,K}^*\\ \end{pmatrix} \begin{pmatrix} \delta_{i,1} h_{i,1} & \cdots & \delta_{i,K} h_{i,L}\\ \end{pmatrix}\]

Sur un batch de \(B\) examples, l’équation se réécrit :

\[\frac{\partial l}{\partial W} = \frac{1}{N} \sum_{i=1}^N \frac{\partial l_i}{\partial W} = \frac{1}{N} \sum_{i=1}^N \delta_i h_i^T \]

ou encore, matriciellement :

\[\frac{\partial l}{\partial W} = \frac{1}{N} H^T \Delta \]

Étape 5 :

Dans le cas de la régression logistique, \(x = h\) et on s’arrête là. Pour un perceptron multi-couche à une couche cachée, il faut encore calculer les gradients pour la couche d’entrée. On note \(h = \sigma(u)\) et \(u = W^h x + b^h\), où \(\sigma\) est la fonction sigmoïde \(x \rightarrow \frac{1}{1+ e^{-x}}\).

\[\frac{\partial L}{\partial W^h} = \frac{1}{N} \sum_{i=1} \underbrace{\frac{\partial l_i}{\partial y_i} \frac{\partial y_i}{\partial s_i}}_{\delta_i} \frac{\partial s_i}{\partial h_i} \frac{\partial h_i}{\partial u_i} \frac{\partial u_i}{\partial W^h} \]

En décomposant, il nous reste à calculer :

\[\frac{\partial s_i}{\partial h_i} = \frac{\partial}{\partial h_i} \left (h_i W + b \right) = W^T % TODO: à redémontrer \]

et :

\[\begin{align} \frac{\partial h_i}{\partial u_i} = \frac{\partial}{\partial u_i} \sigma(u_i) &= \begin{pmatrix} \frac{\partial \sigma(u_{i,1})}{\partial u_{i,1}} & \cdots & \frac{\partial \sigma(u_{i,1})}{\partial u_{i,L}}\\ \vdots & \ddots & \vdots\\ \frac{\partial \sigma(u_{i,L})}{\partial u_{i,1}} & \cdots & \frac{\partial \sigma(u_{i,L})}{\partial u_{i,L}} \end{pmatrix} = \begin{pmatrix} \frac{\partial \sigma(u_{i,1})}{\partial u_{i,1}} & \cdots & 0\\ \vdots & \ddots & \vdots\\ 0 & \cdots & \frac{\partial \sigma(u_{i,L})}{\partial u_{i,L}} \end{pmatrix} \\ &= \text{diag}_k \left( \frac{\partial \sigma(u_{i,k})}{\partial u_{i,k}} \right) = \text{diag}_k \left(\sigma(u_{i,k}) \cdot (1 - \sigma(u_{i,k}) \right) % TODO: à vérifier + détailler \end{align} \]

En effet, la dérivée de la fonction sigmoïde est :

\[\begin{align} \sigma'(x) &= \left(\frac{1}{1+ e^{-x}}\right)' = - \frac{(1 + e^{-x})'}{(1 + e^{-x})^2} = - \frac{- e^{-x}}{(1 + e^{-x})^2} = \underbrace{\frac{1}{1 + e^{-x}}}_\text{sigmoïde} \cdot \frac{e^{-x}}{1 + e^{-x}}\\ &= \sigma(x) \left(\frac{1 + e^{-x} - 1}{1 + e^{-x}} \right) = \sigma(x)\left(\underbrace{\frac{1 + e^{-x}}{1 + e^{-x}}}_{1} - \underbrace{\frac{1}{1 + e^{-x}}}_\text{sigmoïde}\right)\\ &= \sigma(x) \left(1 - \sigma(x)\right) \end{align} \]

Finalement, on peut calculer le gradient par rapport à \(W^h\) :

\[\frac{\partial l_i}{\partial W^h} = \frac{\partial l_i}{\partial u_i} \frac{\partial u_i}{\partial W^h} = x_i^T \delta_i W^T \odot \sigma(u_i) \odot (1 - \sigma(u_i)) % TODO: finaliser \]

---

[1Cyb89]

George Cybenko. Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals and Systems, 2(4):303–314, December 1989. doi:10.1007/BF02551274.

[1LBH15]

Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. Nature, 521(7553):436–444, May 2015. doi:10.1038/nature14539.

[1Lin70]

Seppo Linnainmaa. The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors. PhD thesis, Helsinki University, 1970.

[1MP69]

Marvin Minsky and Seymour A. Papert. Perceptrons. MIT Press, 1969.

[1RHW86]

D. E. Rumelhart, G. E. Hinton, and R. J. Williams. Learning internal representations by error propagation. In David E. Rumelhart and James L. McClelland, editors, Parallel Distributed Processing, pages 318–362. MIT Press, Cambridge, MA, USA, 1986.

[1Wer82]

Paul J. Werbos. Applications of advances in nonlinear sensitivity analysis. In R. F. Drenick and F. Kozin, editors, System Modeling and Optimization, Lecture Notes in Control and Information Sciences, 762–770. Berlin, Heidelberg, 1982. Springer. doi:10.1007/BFb0006203.