Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.
Cours - Réseaux convolutifs modernes¶
Algorithmes modernes de descente de gradient¶
Comme nous l’avons vu précédemment, les réseaux de neurones profonds sont entraînés à l’aide de l’algorithme de descente de gradient stochastique. Cet algorithme permet de déterminer un minimum d’une fonction \(f\), dans notre cas une fonction de coût, de façon itérative.
Reprenons l’équation de mise à jour des paramètres du réseau de neurones pour l’itération \(t\) :
Cette équation de mise à jour présente deux problèmes. Tout d’abord, la fonction objectif \(f\) peut exhiber des variations rapides selon certaines directions et des variations lentes selon d’autres directions. Dans ce cas, le gradient va être fortement biaisé le long de la direction de variation rapide, ce qui peut provoquer un overshoot et des oscillations autour du minimum local. Formellement, il faut considérer la matrice des dérivées secondes de \(f\), aussi appelé matrice Hessienne :
Si la matrice Hessienne \(H\) est mal conditionnée, c’est-à-dire que le rapport entre sa plus grande et sa plus petite valeur singulière est élevé, alors les variations du gradient sont concentrées selon certaines directions. Il y a ainsi une « vallée », qui est propice aux oscillations lors de la descente de gradient.
Deuxièmement, en pratique nous utilisons la descente de gradient stochastique, ce qui signifie que le gradient réel \(\nabla f\left(\mathbf{w}^{t}\right)\) est remplacé par une approximation sur un batch de \(n\) observations \(\nabla \tilde{f}\left(\mathbf{w}^{t}; \mathbf{x}^t\right) = \frac{1}{n} \sum_{k=1}^n \tilde{f}\left(\mathbf{w}^{t}; x_k^t\right)\). Plus le nombre d’observations dans le batch est faible par rapport au nombre total d’observations, moins cette approximation est fiable. Le hasard peut en effet nous sélectionner un batch constitué d’observations similaires, qui mènent le gradient estimé dans une direction différente de celle du gradient réel.
Plusieurs améliorations ont pour ces raisons été introduites à l’algorithme classique de descente de gradient afin d’améliorer sa convergence en pratique.
Méthodes d’accélération du gradient¶
Momentum¶
Une façon peu coûteuse d’accélérer la convergence de la descente de gradient en luttant contre les oscillations est l’utilisation de la méthode de l’inertie ou momentum [4RHW86]. En plus d’être simple à implémenter, cette variante s’applique à tous les algorithmes de descente de gradient. Il s’agit de conserver une mémoire de la direction du gradient passé à la précédente itération.
Habituellement, la mise à jour des paramètres du modèle s’effectue par :
où \(\Delta^{t+1}\) représente le terme de mise à jour :
La méthode du moment remplace la mise à jour par une moyenne glissante des mises à jour passées, de sorte à lisser les variations du gradient par rapport aux itérations :
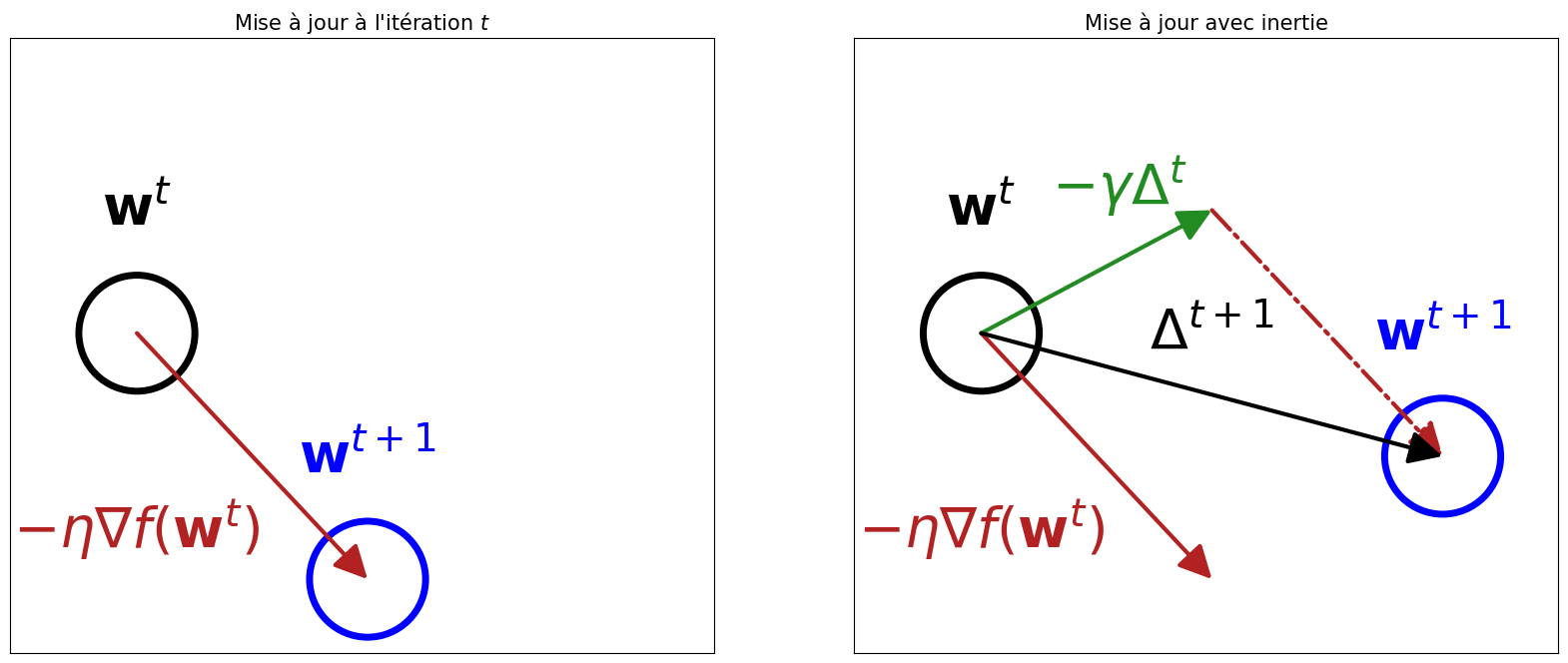
Comparaison de la mise à jour de la descente gradient avec et sans inertie.¶
Pour obtenir le terme de mise à jour total (en noir), la méthode du momentum ajoute au gradient (en rouge) une partie du déplacement précédent pondérée par \(\gamma\) (en vert), comme si la mise à jour des paramètres conservait une partie de « l’inertie » du mouvement.
Dans les directions pour lesquelles le gradient oscille, \(\Delta^{t+1}\) et \(\Delta^{t}\) se compensent : les oscillations sont amorties. Inversement, dans les directions pour lesquelles le gradient est faible mais cohérent d’une itération à l’autre, la vélocité s’accumule d’itération en itération. Ainsi, la méthode du moment permet à la fois une convergence plus robuste lors de la traversée des plateaux et des points selles, mais aussi de lisser le bruit lié à l’estimation du gradient stochastique.
Gradient accéléré de Nesterov¶
La méthode du momentum peut encore être accélérée en exploitant une simple réécriture. Dans sa formulation précédente, le déplacement dans l’espace des paramètres s’effectue d’abord à partir du gradient de \(f\) calculé à la position \(\mathbf{w}^t\), puis l’on ajoute le déplacement correspondant à l’inertie \(\gamma \Delta^t\). Pour gagner une étape, il suffit d’inverser l’ordre de ces opérations. Dans le gradient accéléré de Nesterov, on commence d’abord par se déplacer selon l’inertie \(\gamma \Delta^t\), puis on calcule le gradient de \(f\) à cette nouvelle position, avant de se déplacer selon celui-ci.
En pratique, cela correspond à réécrire la formule de mise à jour par :
En réécrivant \(\mathbf{x}^t = \mathbf{w}^t - \gamma \Delta^{t}\), il est possible de simplifier encore un peu la règle de mise à jour :
Cette mise à jour « anticipée » permet d’éviter des mises à jour de trop grande amplitude lorsque l’inertie passée et le gradient vont dans la même direction. L’optimiseur est plus réactif à la surface de la fonction objectif, ce qui réduit l”overshooting.

Pas d’apprentissage adaptatifs¶
La principale difficulté restante des algorithmes de descente de gradient réside dans le choix de l’hyperparamètre \(\eta\), c’est-à-dire le pas d’apprentissage. En réalité, on souhaiterait avoir un pas d’apprentissage grand lorsque l’on traverse des zones de faible amplitude de gradient, comme des plateaux, un pas d’apprentissage modéré lorsque le gradient est de forte amplitude pour converger rapidement sans overshoot et un pas d’apprentissage faible lorsque l’on s’approche du minimum. Il est possible de définir des politiques de modification du pas d’apprentissage durant l’entraînement, par exemple 10000 itérations avec \(\eta = 0.1\) puis 5000 itérations avec \(\eta = 0.01\). Toutefois, cela introduit de nouveaux hyperparamètres complexes à valider. Une solution attractive serait de laisser à l’algorithme d’optimisation le soin de choisir un pas d’apprentissage adapté en fonction de la surface de la fonction objectif.
Adagrad: Adaptive Gradient¶
L’idée d’Adagrad [4DHS11] consiste à adapter le pas d’apprentissage pour chaque paramètre, en fonction de la surface de la fonction de coût. Commençons par réécrire la règle de mise à jour pour chaque paramètre individuel \(w_i\):
Notons \(g_i^t = \frac{\partial f}{\partial w_i} (w_i^t)\) le gradient de la fonction de coût selon une seule composante, c’est-à-dire le paramètre \(w_i\). Nous pouvons alors définir l’historique des gradients au carré pour la i-ième composante, c’est-à-dire :
Adagrad remplace alors le terme habituel de mise à jour en divisant le pas d’apprentissage pour le i-ième paramètre par \(\sqrt{G_i^t}\) :
Intuitivement, si \(G_i^t\) est grand alors eta_i diminue et inversement. Cela signifie que les mises à jours importantes des paramètres sont atténuées et les petites modifications sont amplifiées. En général, \(\varepsilon \sim 10^{-8}\) et \(\eta \sim 10^{-2}\).
Toutefois, Adagrad a un inconvénient. Comme \((g_i^t)^2 \geq 0\), la somme des gradients passés au carré \(\frac{1}{G_i^t}\) décroît de façon monotone lorsque \(t\) augmente. Autrement dit, au fur et à mesure des itérations, le pas d’apprentissage devient de plus en plus faible, ce qui peut stopper prématurement la convergence de l’algorithme en stoppant les mises à jours.
RMSProp (Root Mean Square Propagation) [4TH12] est une variante d’Adagrad qui consiste calculer l’historique des carrés des gradients non pas depuis le début de l’apprentissage \(t=0\), mais seulement sur une fenêtre à l’aide d’une moyenne glissante. Il s’agit donc du même algorithme que Adagrad, avec pour seule différence que \(G_i^t\) est remplacé par :
et la règle de mise à jour de Adagrad est inchangée :
\(\tilde{G}_i^t\) n’est plus une fonction croissante monotone, ce qui supprime en conséquence la décroissance agressive du pas d’apprentissage qui existait dans Adagrad. L’optimiseur RMSProp demeure assez populaire, notamment pour les réseaux de neurones récurrents.
Adam: Adaptive Moment Estimation¶
Adam [4KB15] est l’algorithme de descente de gradient à pas adaptatif le plus courant à l’heure actuelle. En schématisant, il s’agit d’une combinaison de RMSProp et de la méthode du momentum. Adam nécessite deux hyperparamètres \(\beta_1, \beta_2\) contrôlant le calcul des moments statistiques de 1er et 2ème ordre du gradient (moyenne et variance) de façon glissante.
L’estimation de la moyenne empirique du gradient sur les dernières itérations aura un effet similaire au momentum :
Tandis que la normalisation par la variance empirique aura un effet semblable à Adagrad/RMSProp :
Le terme de mise à jour est ainsi remplacé par :
Construire des réseaux plus profonds¶
Architectures profondes et gradients évanescents¶
Comme nous l’avons vu précédemment, les architectures de réseaux convolutifs développées depuis 2012 tendent à comprendre de plus en plus de couches. Ainsi, l’architecture AlexNet (2012) ne comporte que 8 couches. À titre de comparaison, nous pouvons regarder les architectures arrivées en tête de la compétition de reconnaissance d’objet ILSVRC les années suivantes. En 2014, les modèles vainqueurs sont VGG-19 (19 couches) et GoogLeNet (22 couches). En 2015, il s’agit de ResNet avec 152 couches ! L’augmentation du nombre de couches s’accompagne d’une complexité croissante. Non seulement le nombre de paramètres dans les modèles explose, mais les hyperparamètres deviennent également beaucoup plus nombreux. En outre, le problème des gradients évanescents va rapidement se poser.
Une première tentative de standardisation de la construction des modèles convolutifs est l’approche VGG. En observant qu’empiler plusieurs couches convolutives de noyaux \(3\times3\) est équivalent à une seule couche de noyau plus grand (par exemple, \(7\times7\)), VGG adopte la notion de « blocs » convolutifs. Un bloc est ainsi constitué de :
Deux ou trois couches convolutives de noyaux \(3\times3\), avec un pas de 1 et un padding de 1.
Toutes les convolutions au sein du bloc ont le même nombre de filtres (c’est-à-dire la même « largeur »).
Le nombre de canaux en sortie du bloc est égal au double du nombre de canaux d’entrée, ou identique au nombre de canaux d’entrée si la taille désirée est atteinte.
Une non-linéarité ReLU est appliquée après chaque couche.
La sortie du bloc passe dans un maxpooling \(2\times2\).
Cette standardisation permet de réduire le nombre d’hyperparamètres à chercher. Ainsi, un bloc convolutif divise par 2 les dimensions de l’entrée en hauteur et en largeur, et multiplie par 2 le nombre de canaux. Pour réduire encore plus les dimensions spatiales, il suffit d’empiler plus de blocs. Une fois la dimension souhaitée atteinte, on ajoute à la fin du modèle un perceptron multi-couches avec deux couches cachées pour réaliser la classification finale.
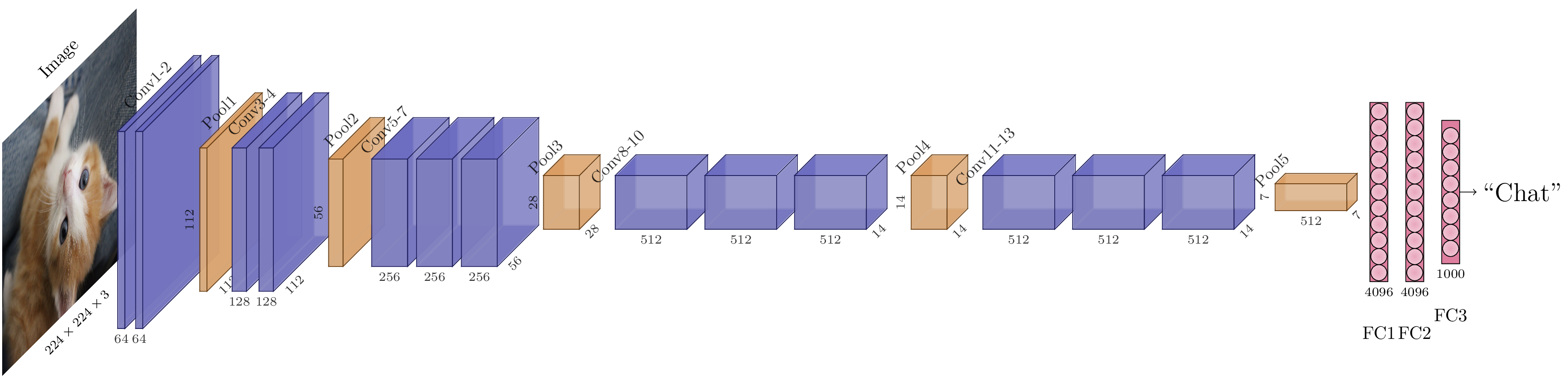
Architecture VGG-16. Elle peut se décrire plus simplement avec des blocs : un bloc de 2 convolutions (largeur 64), un bloc de 2 convolutions (largeur 128), un bloc de 3 convolutions (largeur 256), un bloc de 3 convolutions (largeur 512), un bloc de 3 convolutions (largeur 512), un classifieur à deux couches cachées. Pour obtenir VGG-19, il suffit d’ajouter un bloc de 3 convolutions de largeur 512 au milieu du modèle.¶
Pour contourner le problème des gradients évanescents, les CNN profonds utilisent la fonction d’activation ReLU, qui est non-saturante. Néanmoins, ce n’est pas suffisant pour les modèles très profonds (au-delà d’environ vingt de couches), qui souffrent encore de gradient évanescent. Trois solutions sont possibles : forcer la rétropropagation d’un gradient à l’aide d’un classifieur auxiliaire (solution GoogLeNet), normaliser les activations (BatchNorm) ou introduire des connexions court-circuit (solution ResNet). Nous allons voir les deux premières solutions et nous aboderons la troisième plus tard.
Normalisations¶
Batch Normalization¶
La normalisation par lot ou batch normalization est une méthode permettant d’accélérer la convergence des réseaux profonds et de réduire l’influence de l’initialisation. La batch normalization est une opération appliquée sur les activations en sortie d’une couche par centrage et réduction. Considérons un batch (lot) de \(K\) activations \(\{\mathbf{z}^{(1)}, \mathbf{z}^{(2)}, \dots, \mathbf{z}^{(K)}\}\), chaque activation étant de dimension \(d\), c’est-à-dire \(\mathbf{z}^{(k)} = \left(z_1^{(k)}, z_2^{(k)}, \dots, z_d^{(k)}\right)\). Notons \(\tilde{\mu}\) et \(\tilde{\sigma}\) respectivement le vecteur des moyennes et le vecteur des variances empiriques composante par composantes des activations sur le batch:
Alors, la batch normalization applique la transformation définie par :
où \(\epsilon\) est une constante arbitraire positive petite ajoutée pour la stabilité numérique (afin de garantir que le dénominateur soit non-nul).
Durant l’apprentissage, les moments statistiques \(\tilde{\mu}\) et \(\tilde{\sigma}\) sont calculés directement sur le batch. Leurs valeurs sont accumulées par moyenne glissante pendant l’entraînement, puis sont stockées avec les paramètres du modèle pour être réutilisées telles quelles durant l’inférence. Ainsi, durant la phase de test, les valeurs des activations pour une observation ne sont plus dépendantes de la taille du batch.
L’activation ainsi normalisée est donc de moyenne nulle et de variance unitaire, ce qui annule l’effet des biais. En pratique, pour permettre au modèle de retrouver son expressivité complète, la batch normalization est suivie par une fonction affine de paramètres \(\gamma_i\) et \(\beta_i\) appris durant l’entraînement :
Augmentation de données¶
Comme vu en introduction, augmenter le nombre d’observations dans le jeu d’apprentissage permet d’améliorer la borne de généralisation, c’est-à-dire de réduire l’écart entre l’erreur d’apprentissage et l’erreur de généralisation. S’il n’est généralement pas possible de facilement collecter de nouvelles données annotées, il est parfois facile de générer des observations additionnelles. En effet, pour de nombreux problèmes, l’étiquette de supervision est inchangée même après un certain nombre de transformations appliquées sur l’observation initiale. Par exemple, dans le cas des images, des déformations géométriques (translations, rotations) ou perceptuelles (changements de couleur ou floutages) ne changent pas la catégorie des objets qui sont représentés. Ces invariances vont nous permettre de générer de nouveaux exemples d’apprentissage en altérant les images existantes. Ce procédé est appelé augmentation de données.

Quelques exemples d’augmentations d’image classiques, appliquées sur une photographie de l’astronaute Eileen Collins (1956-). Les paramètres des transformations sont aléatoires : intensité du flou, angle de la rotation, amplitude du rognage, etc. Il est possible de combiner plusieurs augmentations pour augmenter encore le nombre d’exemples.¶
Les approches classiques d’augmentation de données sont généralement d’ajouter du bruit aux données (par exemple, un bruit gaussien) ou tout autre type de dégradation volontaire. En plus d’améliorer la généralisation du modèle en augmentant le nombre d’exemples, ces augmentations permettent aussi d’améliorer la robustesse du modèle aux transformations utilisées pour augmenter les données.
Apprentissage par transfert¶
Transfer learning¶
Fine-tuning¶
John Duchi, Elad Hazan, and Yoram Singer. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. Journal of Machine Learning Research, 12(Jul):2121–2159, 2011.
Diederik Kingma and Jimmy Ba. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR). 2015. arXiv:1412.6980.
D. E. Rumelhart, G. E. Hinton, and R. J. Williams. Learning internal representations by error propagation. In David E. Rumelhart and James L. McClelland, editors, Parallel Distributed Processing, pages 318–362. MIT Press, Cambridge, MA, USA, 1986.
Tijmen Tielman and Geoffrey Hinton. Lecture 6.5—RmsProp: Divide the gradient by a running average of its recent magnitude. 2012.
