Cours - Réduction de l’ordre de complexité

[Diapositives du cours]

Une seconde famille de méthodes permettant de réduire le volume de calculs travaille sur toutes les données (et variables) mais en exploitant leurs caractéristiques de similarité afin de diminuer l’ordre de complexité des calculs à faire. En effet, les modèles décisionnels sont souvent « locaux ». La décision pour une nouvelle donnée dépend principalement (et parfois exclusivement) des données étiquetées proches.

Par exemple, pour une décision sur la base des k plus proches voisins, seules comptent les k données étiquetées les plus proches de la nouvelle donnée \(q\) à laquelle il faut affecter une étiquette de classe :

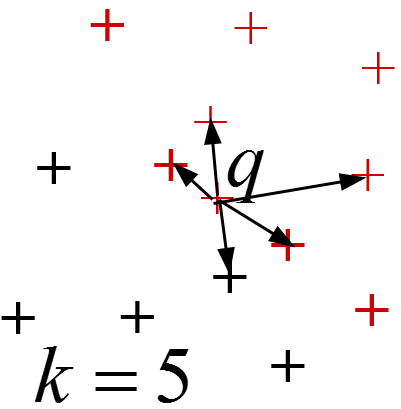
Dans la suite de ce chapitre, après une présentation rapide du principe de la réduction de l’ordre de complexité et un passage en revue des problèmes ciblés, nous examinerons de plus près le hachage sensible à la similarité (Locality Sensitive Hashing, LSH).

Principe des méthodes et typologie des besoins

Grâce à la construction préalable d’un index multidimensionnel ou métrique il est parfois possible de réduire l’ordre de complexité des calculs à faire, par exemple \(O(N) \rightarrow O(\log(N))\) ou \(O(1)\), \(O(N^2) \rightarrow O(N\log(N))\), \(N\) étant le nombre total de données. Ces méthodes peuvent être exactes (fournir les mêmes résultats qu’un calcul exhaustif) ou, plus souvent, approximatives. En revanche, ces méthodes deviennent peu efficaces (réduction insuffisante de la complexité et même augmentation du coût) lorsque le nombre de variables décrivant les données est élevé. Aussi, leur mise en œuvre efficace sur une plate-forme distribuée peut poser quelques difficultés, ce qui explique certaines réserves dans leur implémentation.

Des combinaisons de méthodes de réduction de complexité peuvent également être intéressantes. Par exemple, appliquer une réduction de dimension avant la réduction de l’ordre de complexité permet de diminuer l’impact de la malédiction de la dimension sur la structure d’index employée ; nous y reviendrons ultérieurement.

Examinons d’abord brièvement les principaux types de problèmes pour lesquels une réduction de l’ordre de complexité est envisageable :

1. Recherche par similarité.

2. Décision : k plus proches voisins, machine à noyaux.

3. Estimation de densité (pour la description ou la décision).

4. Classification automatique, quantification.

5. Jointure par similarité.

6. Apprentissage supervisé, apprentissage semi-supervisé, apprentissage actif.

Ce bref examen a pour seul objectif de montrer la large applicabilité des méthodes de réduction de l’ordre de complexité et non d’expliquer dans le détail les solutions aux problèmes considérés (dont certains feront l’objet de chapitres suivants).

La recherche par similarité a plusieurs applications dans la fouille de données ou dans la prise de décision (par ex. sur la base des k plus proches voisins), ainsi que des applications directes comme la recherche de plagiat, l’authentification biométrique, les systèmes de recommandation, les systèmes d’information géographiques.

Plusieurs types de recherche sont habituellement mis en œuvre (\(\mathbf{q}\) est la requête, c’est à dire la donnée à laquelle il faut trouver, dans une base \(\mathcal{D}\), d’autres données similaires):

1. La recherche par intervalle (range query) : \(Range_r(\mathbf{q}) = \{\mathbf{x} \in \mathcal{D} | \forall i, \left|x_i - q_i\right| \leq r_i\}\)

2. La recherche dans un rayon (sphere query) : \(Sphere_{\epsilon}(\mathbf{q}) = \{\mathbf{x} \in \mathcal{D} | d(\mathbf{x},\mathbf{q}) \leq \epsilon\}\)

3. La recherche des k plus proches voisins (kppv, kNN) : \(kNN(\mathbf{q}) = \{\mathbf{x} \in \mathcal{D} | \left|kNN(\mathbf{q})\right| = k \wedge \forall \mathbf{y} \in \mathcal{D}-kNN(\mathbf{q}), d(\mathbf{y},\mathbf{q}) > d(\mathbf{x},\mathbf{q})\}\)

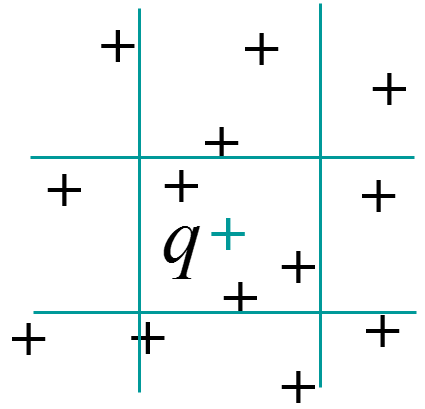
Fig. 22 Recherche dans un intervalle

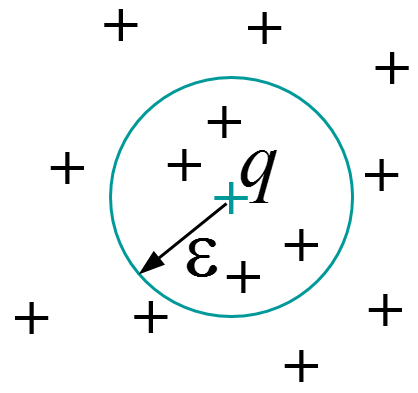
Fig. 23 Recherche dans un rayon

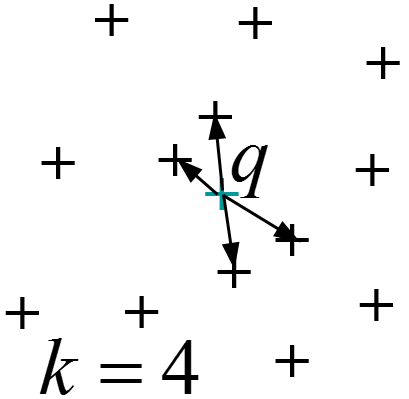
Fig. 24 Recherche des kppv (kNN)

Si \(N\) est le nombre de données de \(\mathcal{D}\), on souhaite disposer d’une méthode de recherche de complexité inférieure à la complexité \(O(N)\) (linéaire en \(N\)) d’une recherche exhaustive.

La prise de décision sans modèle (par ex. sur la base des k plus proches voisins) ou avec un modèle peut avoir une complexité élevée si une méthode naive d’évaluation est adoptée. Considérons deux cas pour illustrer :

1. Pour la décision sur la base des k plus proches voisins il est d’abord nécessaire de trouver les kppv de la nouvelle donnée \(\mathbf{x}\) à affecter à une classe, ensuite de faire voter ces kppv (vote à la majorité simple ou qualifiée, avec ou sans rejet d’ambiguïté). La recherche exhaustive des kppv a une complexité \(O(N)\) (\(N\) étant le nombre de données).

2. La fonction de décision d’une machine à noyaux (par ex. machine à vecteurs support ou analyse discriminante à noyaux) est : \(f^*(\mathbf{x}) = \sum_{i=1}^N \alpha_i^* y_i K(\mathbf{x},\mathbf{x}_i) + b^*\). Pour un problème de discrimination à deux classes, la nouvelle donnée \(\mathbf{x}\) sera affectée à une des classes suivant le signe de \(f^*(\mathbf{x})\). Si \(N\) est le nombre de données \(\mathbf{x}_i\) (nombre de vecteurs support pour une SVM, ou nombre total de données étiquetées pour l’analyse discriminante à noyaux) alors un calcul exhaustif est de complexité \(O(N)\). Or, si des noyaux locaux sont employés (\(K(\mathbf{x},\mathbf{x}_i) \approx 0\) pour \(d(\mathbf{x},\mathbf{x}_i) > \epsilon\), par ex. pour la loi normale multidimensionnelle), alors seuls comptent les \(\mathbf{x}_i\) dans un rayon \(\epsilon\) autour de \(\mathbf{x}\), il est donc possible de réduire l’ordre de complexité par rapport au calcul exhaustif.

Fig. 25 \(k\) plus proches voisins

Fig. 26 Machine à noyaux

L’estimation de densité non paramétrique (par ex. par noyaux de Parzen) ou paramétrique (par ex. par mélange additif gaussien) peut être employée aussi bien dans l’analyse exploratoire que dans la modélisation décisionnelle. Pour examiner la complexité de l’estimation de densité, prenons deux exemples :

1. Noyaux de Parzen : noyaux \(K\) identiques centrés sur les \(N\) observations initiales, la densité en \(\mathbf{x}\) est \(f(\mathbf{x}) \propto \sum_{i=1}^N K(\mathbf{x},\mathbf{x}_i)\).

2. Mélange additif gaussien : la densité en \(\mathbf{x}\) est une somme pondérée de lois normales multidimensionnelles (les lois du mélange), on note par \(N\) le nombre de lois dans le mélange. Pour des données massives la valeur de \(N\) peut être élevée.

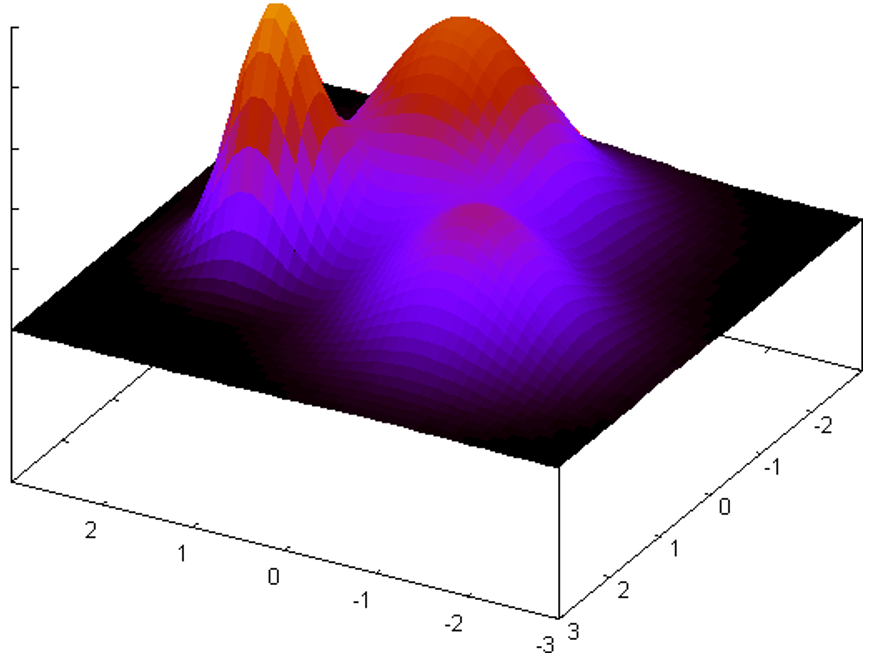
Fig. 27 Estimation de densité par un mélange additif de lois normales bidimensionnelles

Dans les deux cas, un calcul exhaustif de la densité en \(\mathbf{x}\) est de complexité \(O(N)\). Ici encore, si des noyaux locaux (ou lois à décroissance rapide, comme la loi normale) sont employés (\(K(\mathbf{x},\mathbf{x}_i) \approx 0\) pour \(d(\mathbf{x},\mathbf{x}_i) > \epsilon\)), alors seuls comptent les \(\mathbf{x}_i\) dans un rayon \(\epsilon\) autour du point \(\mathbf{x}\) dans lequel on cherche à estimer la densité, il est donc possible de réduire l’ordre de complexité par rapport au calcul exhaustif.

La classification automatique est très utile pour mettre en évidence une structure simple (partitionnement ou hiérarchie de partitionnements) dans les données. Une méthode simple de classification automatique, qui peut néanmoins donner de bons résultats avec une initialisation convenable, est la méthode k-means (voir le chapitre sur la classification automatique). Chaque groupe est représenté par son centre de gravité. Pour \(N\) données on considère en général qu’il faut utiliser \(O(N^{1/3})\) centres, la complexité de la classification sera donc \(O(N^{4/3})\).

Si les données sont représentées dans un espace métrique non vectoriel, il est possible d’employer la méthode des k-medoids (un centre de gravité ne peut pas être calculé sur des données non vectorielles, un medoid est simplement l’élément le plus « central » d’un groupe). Dans ce cas, la complexité de la classification est plutôt \(O(N^2)\) car l’identification d’un medoid est plus coûteuse que le calcul d’un centre de gravité.

Nous remarquerons aussi qu’en l’absence de groupes « naturels » dans les données, l’application d’une méthode comme k-means produit plutôt une quantification des données qui peut être également le but recherché dans certaines applications.

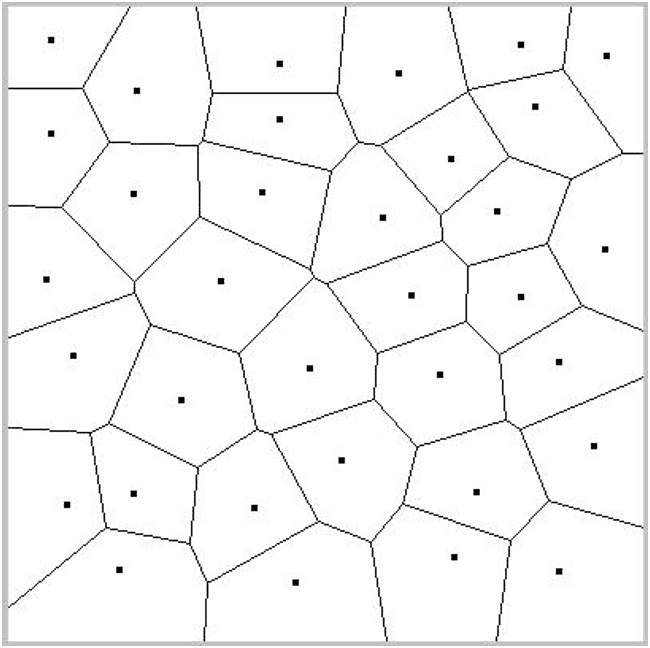
Fig. 28 Quantification vectorielle

Si les calculs de distance entre une donnée et les centres (ou medoids) trop éloignés ont un faible impact sur les résultats, il est envisageable de gagner un facteur de \(N^{1/3}\) dans la complexité de k-means.

Une jointure par similarité entre deux ensembles \(\mathcal{D}_1\) (à \(N_1\) éléments) et \(\mathcal{D}_2\) (à \(N_2\) éléments), avec un seuil de distance \(\theta\), permet de trouver les paires d’éléments des deux ensembles qui sont à une distance inférieure au seuil, c’est à dire \(K_{\theta} = \{(\mathbf{x},\mathbf{y}) | \mathbf{x} \in \mathcal{D}_1, \mathbf{y} \in \mathcal{D}_2, d(\mathbf{x},\mathbf{y}) \leq \theta\}\). On parle d’auto-jointure lorsque \(\mathcal{D}_1 \equiv \mathcal{D}_2\) (\(N_1 = N_2 = N\)). Cette opération est utilisée pour identifier des quasi-copies de documents, pour exclure des analyses ultérieurs les données qui n’ont pas de voisins proches, etc.

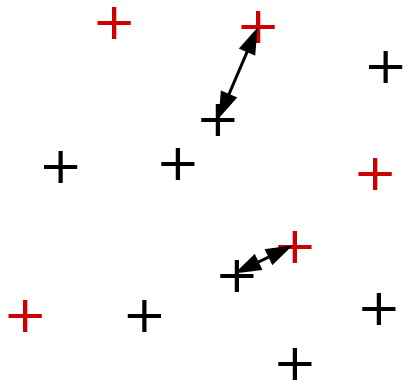
Fig. 29 Jointure par similarité

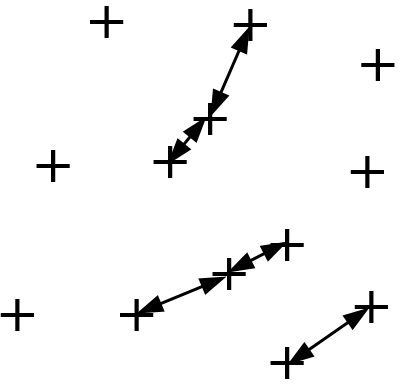
Fig. 30 Auto-jointure par similarité

Si des comparaisons exhaustives sont employées, la complexité de la jointure par similarité est de \(O(N_1 \times N_2)\) et celle de l’auto-jointure de \(O(N^2)\). Une réduction de la complexité à \(O(N \log N)\) ou même \(O(N)\) est envisageable si les comparaisons entre données trop éloignées peuvent être évitées.

L’apprentissage supervisé consiste à construire un modèle décisionnel à partir de données étiquetées \(\{\mathbf{x}_i, y_i\}_{1 \leq i \leq N}\). Par exemple, pour un \(\nu\)-SVM, la détermination des vecteurs de support et de leurs coefficients revient à résoudre le problème d’optimisation sous contraintes suivant :

\[\begin{split}\begin{array}{l} \min_{\alpha} \sum_{i,j=1}^N \alpha_i \alpha_j y_i y_j K(\mathbf{x}_i,\mathbf{x}_j)\\ 1/N \geq \alpha_i \geq 0, 1 \leq i \leq N\\ \sum_{i=1}^N \alpha_i y_i = 0\\ \sum_{i=1}^N \alpha_i \geq \nu \end{array}\end{split}\]

Fig. 31 Modèle de discrimination à 2 classes appris à partir des données étiquetées (représentées par les points) ; la frontière de décision est représentées par les courbes blanches et l’intérieur des classes par la couleur verte et respectivement rouge

Avec \(N\) données d’apprentissage \(\{\mathbf{x}_i, y_i\}\) la complexité est de \(O(N^2)\). En revanche, si le noyau est local (\(K(\mathbf{x}_i,\mathbf{x}_j) \approx 0\) pour \(d(\mathbf{x}_i,\mathbf{x}_j) > \epsilon\)) alors il n’est pas nécessaire de calculer \(K(\mathbf{x}_i,\mathbf{x}_j)\) pour des données \(\mathbf{x}_i\), \(\mathbf{x}_j\) trop éloignées, la complexité peut éventuellement être réduite à \(O(N \log N)\) ou \(O(N)\).

L’apprentissage semi-supervisé vise à utiliser, pour la construction d’un modèle décisionnel, non seulement les données étiquetées, en général relativement peu nombreuses, mais aussi les données non étiquetées disponibles, souvent bien plus nombreuses (\(N\) désignera ici le nombre de données non étiquetées). Par exemple, pour l’apprentissage transductif avec SVM on cherche à maximiser la marge non seulement par rapport aux données étiquetées mais aussi par rapport aux données non étiquetées en considérant, parmi tous leurs étiquetages possibles, le plus « favorable » (voir la figure de gauche ci-dessous). Il faudra s’intéresser pour cela aux seules données non étiquetées qui sont proches de la frontière de décision définie à partir des données étiquetées. Afin d’identifier ces données, une approche naïve consiste à évaluer la fonction de décision (obtenue sur les données étiquetées) pour chacune des \(N\) données non étiquetées. Si on dispose d’une méthode simple pour exclure les données non étiquetées trop éloignées de la frontière, alors la complexité peut être réduite à un ordre inférieur à \(O(N)\).

Dans l’apprentissage actif on considère que l’utilisateur peut donner des étiquettes à des données non encore étiquetées afin d’améliorer le modèle décisionnel existant. Il est nécessaire de faire le meilleur usage possible de ces interactions (coûteuses) entre le système et l’utilisateur. Une des solutions proposées consiste à demander à l’utilisateur d’étiqueter les données non encore étiquetées qui sont les plus « ambiguës » (et non redondantes, donc éloignées entre elles), c’est à dire les plus proches de la frontière de décision courante (voir la figure de droite ci-dessous pour un apprentissage actif avec SVM). Comme pour l’apprentissage transductif, la complexité de la recherche des données les plus proches de la frontière est de \(O(N)\) mais cette complexité peut éventuellement être réduite si on dispose d’une méthode simple pour exclure les données non étiquetées trop éloignées.

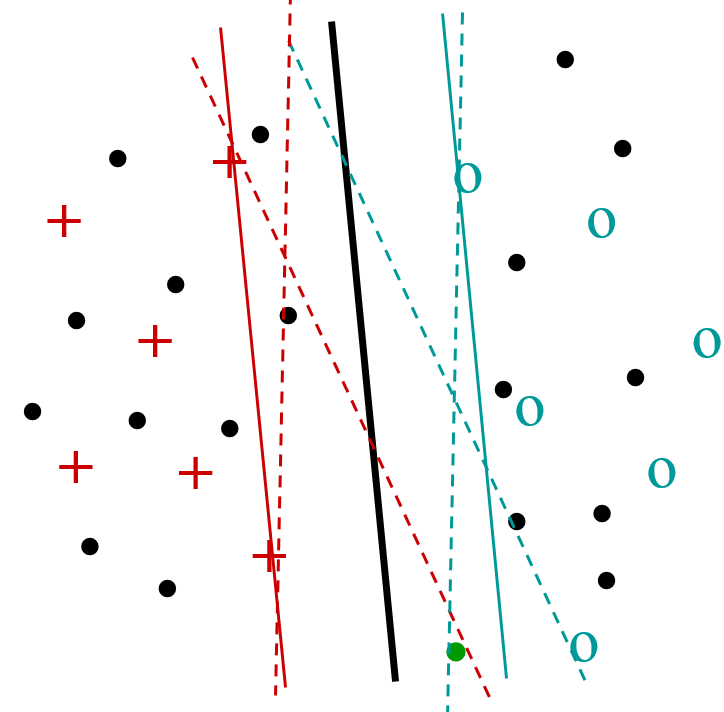
Fig. 32 Transduction avec SVM

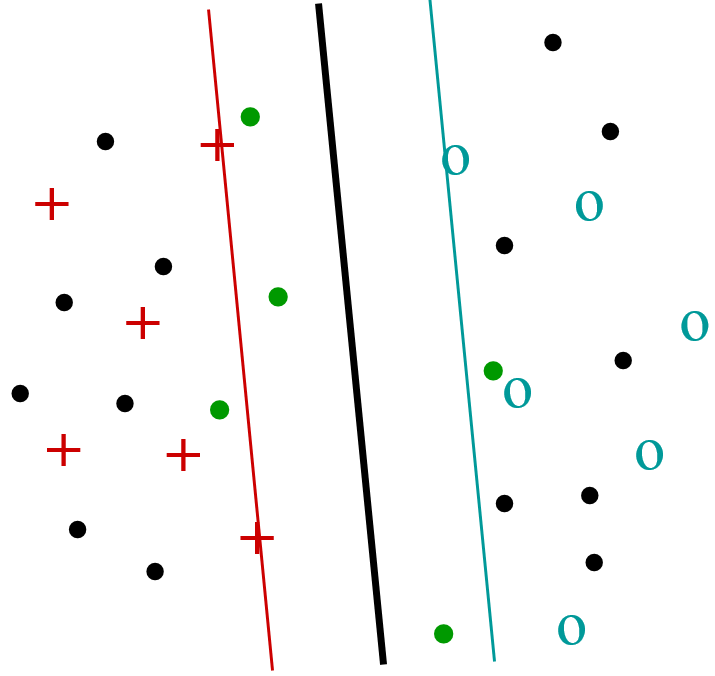
Fig. 33 Apprentissage actif

Pour résumer, les objectifs de réduction de l’ordre de complexité sont :

1. Recherche par l’exemple, décision, estimation de densité (la requête est de même nature que les données) : \(O(N)\) \(\longrightarrow\) \(O(log N)\) ou \(O(1)\).

2. Apprentissage semi-supervisé, apprentissage actif, « recherche par détecteur » (trouver les données les plus proches d’une frontière de décision) : \(O(N)\) \(\longrightarrow\) \(O(log N)\) ou \(O(1)\).

3. Jointure par similarité, apprentissage supervisé à noyaux, N-body problems, certaines méthodes de classification automatique ou de quantification : \(O(N^2)\) \(\longrightarrow\) \(O(N log N)\) ou \(O(N)\).

Il est important de noter ici que la complexité ne peut être inférieure à la taille du résultat obtenu ! Ainsi, une recherche dans un rayon \(\epsilon\) très large, qui couvre la totalité des \(N\) données, ne peut être de complexité inférieure à \(O(N)\) car toutes les données doivent être retournées.

Réduction de l’ordre de complexité : méthodes

Le principe général de la réduction de l’ordre de complexité grâce à la similarité est de regrouper les données par similarité et d’éviter les opérations impliquant des données issues de groupes éloignés. Des structures de données particulières (index multidimensionnels ou métriques) permettent de mettre en œuvre ces regroupements et de sélectionner efficacement, pour chaque donnée (déjà présente dans la base ou nouvelle) vue comme « requête », les données suffisamment proches pour intervenir dans les calculs.

Pour que cette approche générale soit valide, trois hypothèses importantes doivent être satisfaites :

1. Seules les données proches de (ou similaires à) la « requête » sont utiles. Naturellement, si la similarité n’est pas un bon critère de sélection, cette approche est sans intérêt.

2. Très peu de données sont proches de la requête. Comme nous l’avons noté plus haut, la complexité ne peut être inférieure à la taille du résultat obtenu. Si une partie importante des données doit se retrouver dans le résultat, la complexité ne peut pas être réduite.

3. Les données proches de la requêtes sont bien plus proches que les autres. L’approche est basée sur l’élimination, à un coût aussi faible que possible, d’un maximum de données éloignées de la requête. Cela sera d’autant plus facile que les différences de proximité entre les données sont fortes. Cette hypothèse conditionne donc l’efficacité de la méthode de réduction de complexité.

Les figures suivantes illustrent la construction et l’utilisation d’un type d’index particulier, un arbre de recherche. La figure de gauche montre un partitionnement hiérarchique des données. Au niveau le plus grossier nous trouvons trois grandes partitions, A, B et C (A et C ne sont pas représentées en entier). A l’intérieur de B nous trouvons trois partitions plus fines, D, E et F. Cela peut se poursuivre (par ex. G est une sous-partition de D). Une recherche par similarité avec la requête q, dans un rayon (cercle vert dans la figure), se déroule de façon hiérarchique, comme indiqué dans la figure de droite. Un calcul de distance entre q et le centre de A permet de constater que la sphère de recherche (cercle vert ici) ne peut pas intersecter la partition A, toutes les données de A sont donc exclues de la suite de la recherche. Idem pour la partition C. La recherche se poursuit alors dans B par des calculs de distance entre q et les centres des partitions D, E et F. Les données de F sont exclues car il ne peut y avoir d’intersection entre la sphère de recherche et F. La recherche se poursuivra donc dans D et E. Idéalement, l’arbre est traversé du nœud racine (correspondant aux partitions les plus larges) vers les feuilles, sans exploration de branches alternatives. Avec \(N\) données nous avons \(O(N)\) feuilles, donc la longueur d’un chemin descendant (la hauteur de l’arbre) est \(O(log N)\). La complexité de la recherche est alors réduite de \(N\) (avec comparaisons exhaustives) à \(O(log N)\) avec cet arbre de recherche. La complexité de la construction de l’arbre est de \(O(N log N)\), l’utilisation de l’arbre reste intéressante si l’arbre est construit une fois (hors ligne, sans contraintes de temps) et employé ensuite de très nombreuses fois pour répondre à des requêtes sous contraintes de temps.

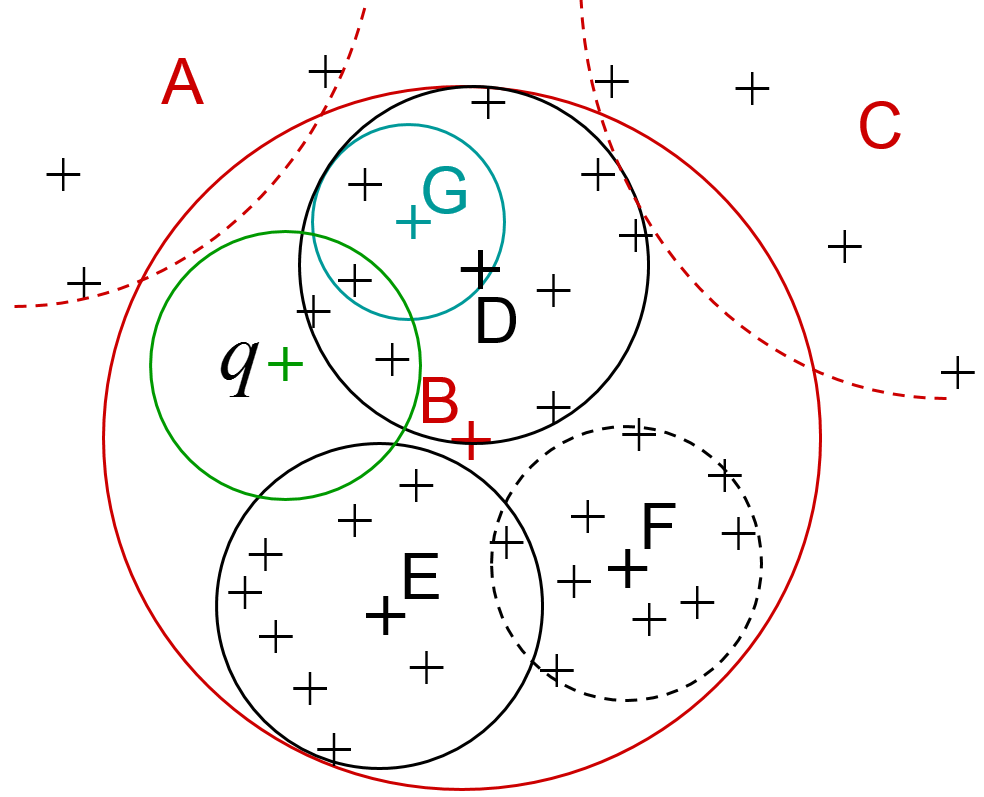
Fig. 34 Partitionnement hiérarchique des données

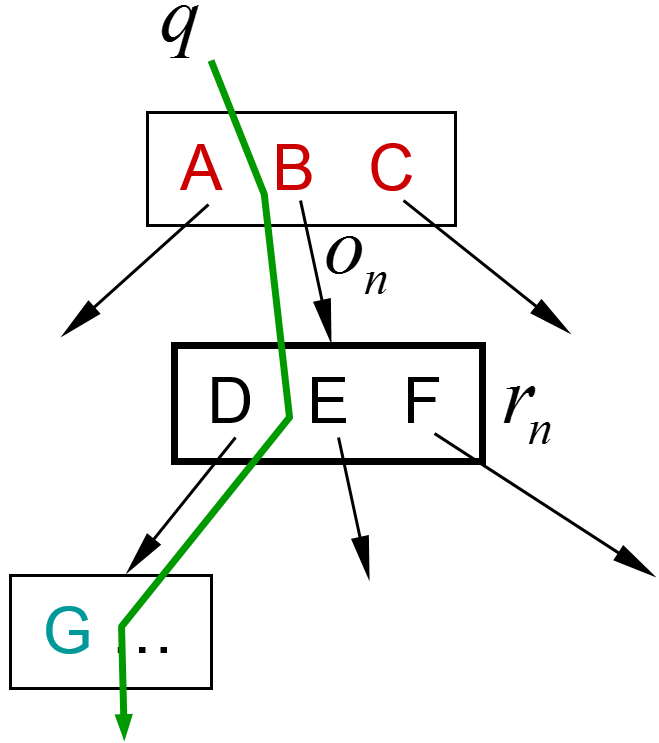
Fig. 35 Recherche dans une hiérarchie de partitions

Question : Supposons que nous avons \(N\) observations situées toutes dans l’hypercube \([0; 1]^{10}\) et souhaitons trouver les données qui sont à une distance euclidienne inférieure à \(3,5\) d’une requête qui coincide avec l’origine des axes. Quelle peut être la complexité algorithmique de cette recherche ?

1. la complexité peut être \(O(log N)\) avec un arbre de recherche

2. la complexité dépend de la méthode de recherche utilisée

3. la complexité est \(N\) car toutes les observations sont dans le rayon de recherche

De nombreuses structures d’index ont été proposées pour réduire la complexité de la recherche par similarité, qui à son tour peut servir à diminuer la complexité des autres familles de méthodes listées plus haut (décision, estimation de densité, apprentissage, etc.). Pour faire une typologie sommaire de ces propositions on s’intéresse d’abord à la méthode de réduction de l’espace de recherche et on trouve notamment :

1. Partitionnement de l’espace de description (utile lorsque les données « couvrent » bien cet espace) : k-d-B-tree, LSD-tree, etc.

2. Partitionnement des données (utile lorsque les données sont présentes seulement dans certaines parties de l’espace) : R-tree, SR-tree, M-tree, etc.

3. Filtrage des données (utile lorsque la malédiction de la dimension, que nous examinerons dans le prochain chapitre, rend inefficaces les deux approches précédentes) : VA-file, LPC-file, etc.

La plupart de ces structures d’index ont été conçues pour la recherche « exacte » : toutes les données qui satisfont la condition de similarité sont retournées dans les résultats et tous les résultats satisfont la condition de similarité. Certaines méthodes peuvent être modifiées pour faire plutôt une recherche « approximative », plus efficace que la recherche exacte et satisfaisante dans de nombreux cas. D’autres méthodes ont été conçues dès le départ pour la recherche approximative et n’ont pas de variante « exacte ». Nous étudierons de plus près, dans la suite, une de ces méthodes approximatives, la hachage sensible à la similarité (Locality Sensitive Hashing, LSH). Une présentation détaillée de bon nombre d’index multidimensionnels et métriques peut être trouvée dans la monographie [Sam05].

Il faut noter ici que la façon dont les données sont stockées peut avoir un impact majeur sur l’intérêt de l’utilisation d’un index par rapport à une recherche exhaustive. En effet, si les données se trouvent sur un stockage de masse (disque classique ou flash) alors une lecture séquentielle est de plusieurs ordres de grandeur plus rapide qu’une lecture « aléatoire » (voir cette figure), or l’utilisation d’un index multidimensionnel ou métrique implique le plus souvent une lecture aléatoire. Par exemple, si l’emploi d’un index permet une division par 100 du nombre d’opérations à réaliser (et de données à lire) mais la lecture aléatoire est 1000 fois plus lente que la lecture séquentielle, la recherche exhaustive (impliquant une lecture séquentielle) sera env. 10 fois plus rapide que celle utilisant l’index.

Enfin, suivant l’utilisation faite de l’index, il est important de tenir compte de la complexité de la construction de cet index. Par exemple, pour un problème de recherche par similarité, si des recherches doivent être faites à faible coût pour de très nombreuses nouvelles requêtes, il sera utile d’employer un index pour réduire la complexité de chaque recherche de \(O(N)\) à \(O(\log N)\) même si la construction de l’index (réalisée une fois, en amont, hors ligne) est \(O(N \log N)\). En revanche, construire un tel index pour réduire la complexité d’une seule classification automatique de \(O(N^{4/3})\) à \(O(N)\) ne sera pas intéressant.

Le hachage

Supposons que nous souhaitons associer à chaque donnée d’un ensemble \(\mathcal{D}\) (appelé en général ensemble des clés) une donnée d’un autre ensemble \(\mathcal{C}\). Si les données de \(\mathcal{D}\) sont simples (par exemple, chaque donnée est un entier) il est possible de s’en servir comme indice dans un tableau qui stocke les valeurs correspondantes de \(\mathcal{C}\).

En revanche, si chaque donnée de \(\mathcal{D}\) est relativement complexe (par exemple, chaîne de caractères de longueur variable, etc.) on peut employer une table d’association avec une colonne pour \(\mathcal{D}\) et une autre pour \(\mathcal{C}\) ; afin de trouver la donnée de \(\mathcal{C}\) correspondant à \(v \in \mathcal{D}\) il suffit de comparer \(v\) successivement aux différentes entrées de la colonne pour \(\mathcal{D}\) et, lorsqu’il y a identité, de lire la donnée associée dans la colonne pour \(\mathcal{C}\). La complexité de cette opération est \(O(N)\) (avec \(N\) la cardinalité de \(\mathcal{D}\)), ce qui est coûteux si \(N\) est élevé. Ce serait intéressant de pouvoir calculer directement (complexité \(O(1)\)), à partir de \(v \in \mathcal{D}\), l’indice dans le tableau où la valeur correspondante de \(\mathcal{C}\) se trouve. C’est ce que font les fonctions de hachage.

Une fonction de hachage \(h\) associe à chaque donnée \(v\) d’un domaine \(\mathcal{D}\) une valeur, souvent de \(\mathbb{Z}^+\) (ensemble des entiers positifs). Cette valeur, appelée hash (ou empreinte, ou condensé) permet d’identifir une case (ou un bloc) mémoire où est stockée la donnée de \(\mathcal{C}\) à associer à \(v\). On parle de collision lorsque la fonction de hachage associe une même valeur de hash à deux valeurs différentes \(v_1,v_2 \in \mathcal{D}\).

Dans les bases de données relationnelles, le hachage est une solution intéressante pour réduire la complexité de la recherche par identité illustrée par l’exemple suivant.

Exemple :

Considérons la table (la relation) Film(titre, realisateur, annee), dans laquelle les valeurs de l’attribut titre sont des chaînes de caractères de longueur variable. Nous souhaitons pouvoir retrouver rapidement le nom du réalisateur et l’année de production à partir du titre d’un film. Supposons que \(p\) pages disque sont nécessaires pour stocker les \(O(N)\) lignes (ou n-uplets, ou enregistrements) de la table Film. Pour cela, un hachage sur l’attribut titre (qui est la clé de hachage) avec la fonction de hachage \(h : \mathcal{D} \rightarrow \{0,1,2,\ldots,p-1\}\) suivante est employé (où \(p\) est un nombre premier) :

\(h (\texttt{titre}) = \left(\sum_{c_i\texttt{ caractère}} ascii(c_i(\texttt{titre}))\right) \mod p\)

A chaque insertion d’un n-uplet dans la table Film, la clé (la valeur de l’attribut titre) est hachée avec \(h\) et le n-uplet est stocké sur la page ainsi identifiée. Si cette page est pleine, des pages de débordement sont utilisées, comme illustré dans la figure suivante (gauche).

Lors d’une recherche, le titre du film est haché avec \(h\), la page identifiée par le hash obtenu est lue, ainsi que ses éventuelles pages de débordement, l’information recherchée doit s’y trouver (si elle est présente dans la table). La complexité de la recherche est donc \(O(1)\) si une seule page disque est lue.

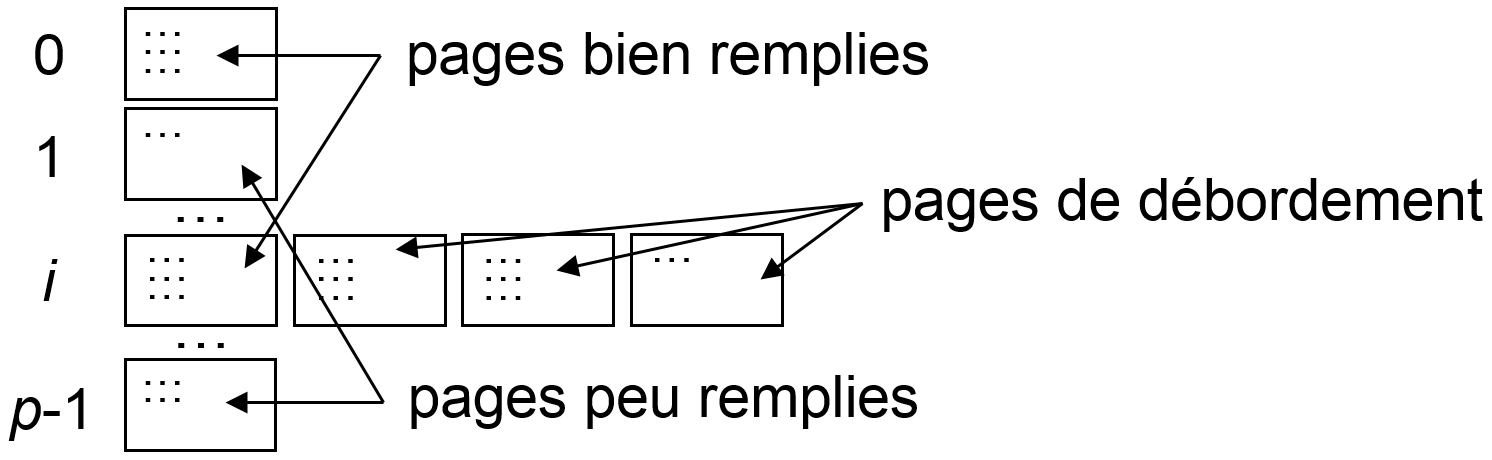
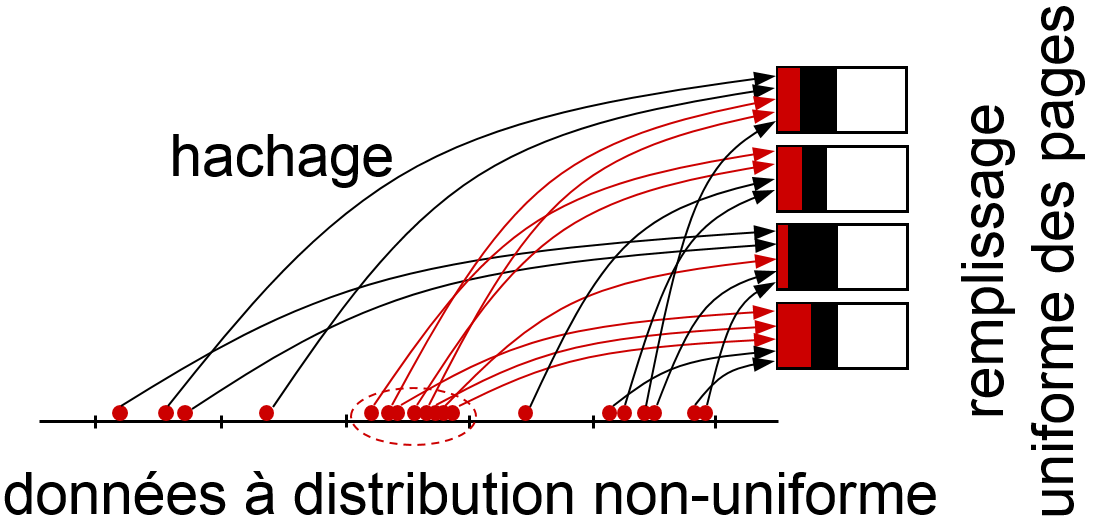
Les données de \(\mathcal {D}\) ont en général une distribution très peu uniforme. Comme le montre cet exemple, les fonctions de hachage utilisées pour ce type de recherche doivent « disperser » le plus uniformément possible les hash associées afin d’optimiser le remplissage des pages : les pages trop peu remplies gaspillent l’espace de stockage, les pages de débordement allongent le temps de recherche. Pour cette raison, la similarité entre les clés (données de \(\mathcal{D}\)) n’est généralement pas conservée entre leurs valeurs de hash (figure précédente, à droite). Ces fonctions de hachage sont donc en général inadaptées à la recherche par intervalle ou par similarité.

Hachage sensible à la similarité (LSH)

Le hachage sensible à la similarité (Locality-Sensitive Hashing, LSH) est une adaptation du hachage à la recherche par similarité. Considérons les données d’un domaine \(\mathcal{D}\) doté d’une métrique \(d_\mathcal{H}:\mathcal{D} \times \mathcal{D} \rightarrow \mathbb{R}^+\), ainsi qu’un ensemble de hash \(\mathcal{Q}\).

Définition :

\(\mathcal{H}=\{h:\mathcal{D} \rightarrow \mathcal{Q}\}\) est un ensemble de fonctions de hachage \((r_1, r_2, p_1, p_2)\)-sensibles (avec \(r_2 > r_1 > 0\), \(p_1 > p_2 > 0\)) si (voir [GIM99]) :

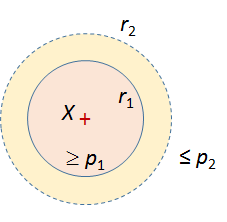
(1)\[\begin{split} \forall x,y \in \mathcal{D}, \begin{array}{l} d_\mathcal{H}(x,y) \leq r_1 \ \Rightarrow \ P_{h \in \mathcal{H}}(h(x) = h(y)) \geq p_1\\ d_\mathcal{H}(x,y) > r_2 \ \Rightarrow \ P_{h \in \mathcal{H}}(h(x) = h(y)) \leq p_2 \end{array}\end{split}\]

La définition exige que la probabilité de collision soit plus forte (\(\geq p_1\), avec \(p_1 > p_2\)) entre données proches (\(d_\mathcal{H}(x,y) \leq r_1\)) qu’entre données plus éloignées (\(\leq p_2\) si \(d_\mathcal{H}(x,y) > r_2\), avec \(r_2 > r_1\)). Cela est illustré dans la figure suivante pour des données de \(\mathcal{D} \subset \mathbb{R}^2\) et la distance euclidienne classique.

LSH peut être employé pour la recherche par similarité de la façon suivante :

1. En amont (avant toute requête) il est nécessaire de :

   1. Calculer la valeur de hash pour chacune des données de la base.

   2. Stocker les données de même valeur de hash dans une même page (appelée aussi bucket) ; utiliser des pages de débordement si nécessaire.

2. Ensuite, pour chaque donnée-requête :

   1. Hachage de la donnée-requête pour obtenir son hash.

   2. Lecture de la page (avec les éventuelles pages de débordement) associée à ce hash.

   3. Retour de toutes les données de cette page, éventuellement après filtrage de ces données par calcul des distances entre la requête et chacune de ces données.

La complexité de la recherche est \(O(1)\) pour chaque requête.

La figure suivante illustre cette méthode. Les points représentés constituent l’ensemble \(\mathcal{D} \subset \mathbb{R}^2\). La grille oblique (en bleu) correspond au partitionnement de \(\mathcal{D}\) en pages (ou buckets) par une fonction de hachage adaptée à la distance euclidienne classique dans \(\mathbb{R}^2\). Les points situés dans un même parallélogramme sont dans une même page (ont une même valeur de hash). Lors de la recherche, les données de même hash que la requête (représentée par le point rouge) sont retournées.

On peut constater que, pour une recherche dans un rayon (cercle de recherche en rouge), certaines données retournées ne sont pas dans le rayon de recherche (constituent les « faux positifs » si le filtrage par calcul de distances n’est pas réalisé) alors que certaines données qui sont dans le rayon de recherche ne se trouvent pas sur la même page et ne sont donc pas retournées (ce sont les « faux négatifs »). Les résultats de la recherche sont donc une approximation de l’ensemble correspondant à la recherche exacte dans le rayon indiqué.

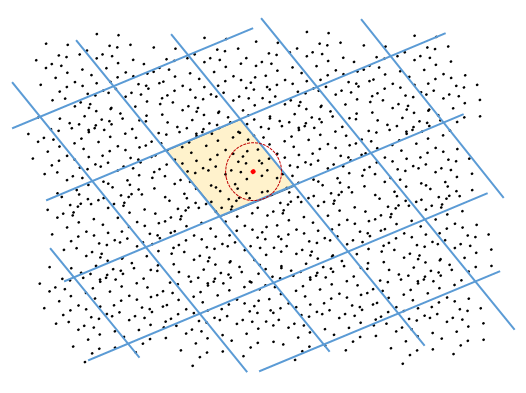
Fig. 36 Données bidimensionnelles, fonction de hachage et requête

LSH pour métriques courantes

Nous passons en revue dans la suite quelques familles de fonctions LSH adaptées à différents types de données et métriques associées.

LSH pour la métrique euclidienne. Considérons des données décrites par \(m\) variables quantitatives, pour lesquelles on emploie la métrique euclidienne classique : \(\mathcal{D} \subset \mathbb{R}^m\), \(d_\mathcal{H}\) est la métrique \(L_2\). Une famille de fonctions LSH \((r_1, r_2, p_1, p_2)\)-sensibles est \(\mathcal{H} = \{h_{\mathbf{a},b,w}:\mathbb{R}^m \rightarrow \mathbb{Z}\}\), \(h_{\mathbf{a},b,w}(\mathbf{x}) = \left\lfloor \frac{\mathbf{a}^T \cdot \mathbf{x} + b}{w} \right\rfloor\) avec \(\mathbf{a} \in \mathbb{R}^m\) de composantes tirées indépendamment suivant \(\mathcal{N}(0,1)\) et \(b \in \mathbb{R}\) tiré suivant la loi uniforme dans \([0, 1)\), \(w \in \mathbb{R}\).

Dans \(\mathbb{R}^2\), une telle fonction de hachage élémentaire correspond à une famille de droites parallèles, comme le montre la figure suivante (gauche). Chaque page de hachage correspond à un domaine borné dans une seule dimension ; sur une même page de hachage que la requête on peut trouver des données éloignées de la requête (« faux positifs »). Aussi, des données similaires à la requête peuvent se trouver sur des pages voisines (et sont donc des « faux négatifs »), surtout lorsque la requête est proche de la droite qui sépare deux pages.

On construit une table de hachage (ou une fonction de hachage composée) en faisant l’intersection entre les pages (buckets) de \(n\) fonctions élémentaires indépendantes ; le hash résultant est un n-uplet d’entiers. La figure suivante (droite) illustre cela dans \(\mathbb{R}^2\), avec 3 fonctions élémentaires. Par rapport à l’utilisation d’une seule fonction élémentaire, l’emploi d’une table de hachage permet de réduire le nombre de faux positifs sans augmenter trop fortement le nombre de faux négatifs.

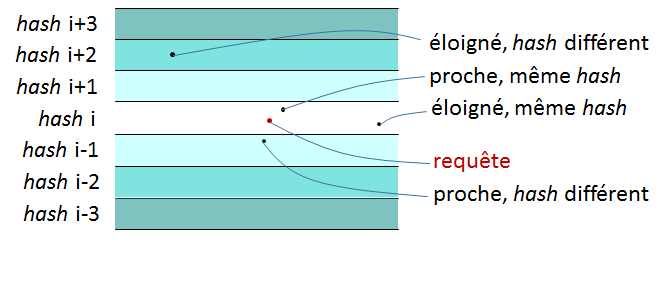
Fig. 37 Fonction LSH élémentaire dans \(\mathbb{R}^2\)

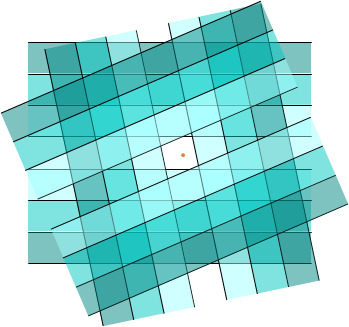
Fig. 38 Composition de 3 fonctions élémentaires

En effet, une fonction élémentaire n’est pas assez sélective car le domaine correspondant à une page est borné dans une seule direction. Pour retenir seulement les données correspondant à la requête (situées à l’intérieur du cercle en rouge sur la figure suivante à gauche) il faut calculer la distance entre la requête et chacune des données de la même page que la requête, ce qui est coûteux. Si ce calcul n’est pas fait, nous obtenons de nombreux « faux positifs » et donc la précision des résultats (le rapport entre le nombre de bons résultats retournés et le nombre total de résultats retournés) sera faible.

Employer une grille plus fine (augmenter \(w\) dans la définition de la fonction, figure suivante au centre) réduira le nombre de « faux positifs » mais augmentera fortement celui de « faux négatifs » car plus de données situées à l’intérieur du cercle ne seront pas retournées. La précision augmentera mais le rappel (le rapport entre le nombre de bons résultats retournés et le nombre total de données de la base satisfaisant la condition de similarité à la requête) diminuera sensiblement.

Construire une table de hachage en composant plusieurs fonctions élémentaires indépendantes permettra d’exclure de nombreux « faux positifs », car les domaines correspondant aux pages de la table seront bornés dans plusieurs directions différentes, tout en augmentant un peu le nombre de « faux négatifs » (figure suivante à droite).

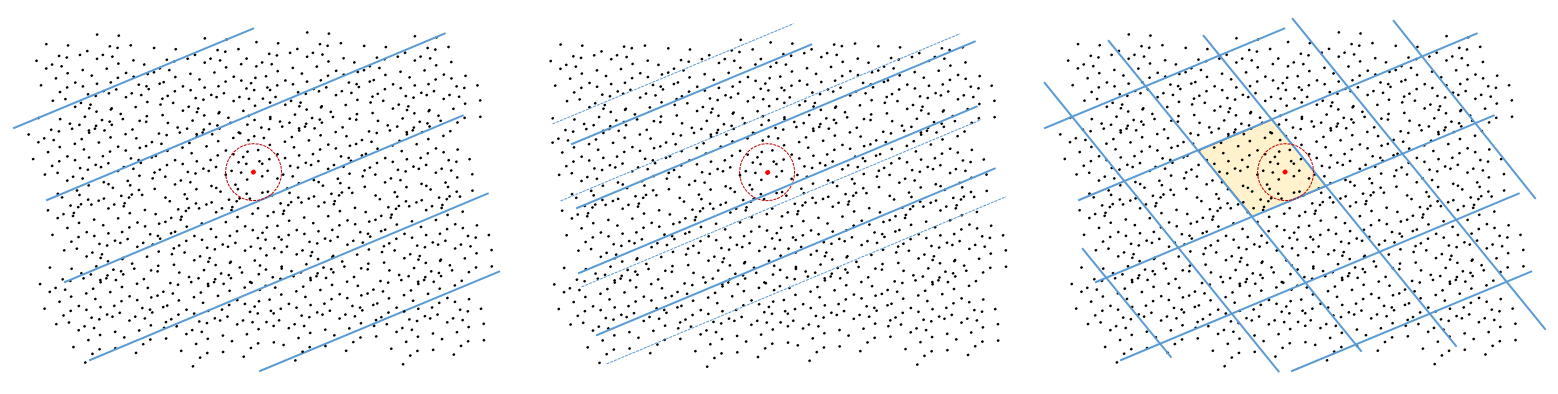
Fig. 39 Composer des fonctions de hachage pour augmenter la précision

Il est important de noter que, dans la pratique, la dimension \(m\) de l’espace est très élevée et le nombre de fonctions de hachage composées dans une même table de hachage est \(n \ll m\). En conséquence, contrairement au cas illustré dans les figures précédentes, les domaines correspondant aux pages de la table ne seront généralement pas bornés dans toutes les directions. Sans filtrage des résultats par calcul des distances, la précision sera en général inférieure à 1 (des données en collision avec la requête sont loin de la requête, donc de « faux positifs »).

Si la requête est proche d’une frontière entre pages, des données proches de la requête sont exclues des résultats car situées sur une page différente de celle de la requête. Dans une table de hachage constituée par la composition de \(n\) fonctions élémentaires, les « faux négatifs » sont d’autant plus nombreux que la requête est proche de l’intersection entre plusieurs frontières.

Une solution pour réduire le nombre de « faux négatifs » (et augmenter donc le rappel) est d’utiliser \(t > 1\) tables de hachage indépendantes (constituées de fonctions élémentaires indépendantes), de retourner à partir de chaque table l’ensemble des données de même hash que la requête et ensuite de faire la réunion de ces \(t\) ensembles. Les tables étant indépendantes, il est probable que les données proches de la requête et qui exclues par une des tables soient retournées grâce à une autre.

La figure suivante illustre l’emploi de 4 tables, chacune constituées de 3 fonctions de hachage élémentaires indépendantes. La requête est le point rouge, proche de certaines frontières dans une table et d’autres frontières dans les autres tables. La réunion des pages couvre relativement bien le voisinage de la requête.

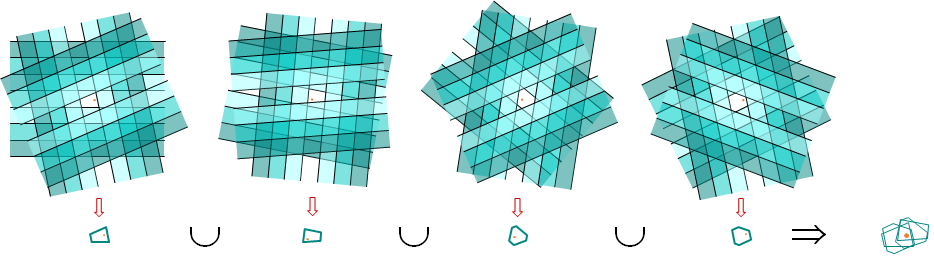
Fig. 40 Composer des tables de hachage pour augmenter le rappel

La composition de plusieurs fonctions de hachage dans une même table de hachage afin d’augmenter la précision et l’utilisation conjointe de plusieurs tables de hachage pour augmenter le rappel seront examinés de façon plus précise dans la section Amplification de fonctions de hachage plus loin.

Multiplier les tables multiplie d’autant le temps nécessaire pour traiter la requête et l’espace nécessaire, car chaque table doit être stockée séparément. Afin de réduire le nombre de tables, Multi-probe LSH (voir [LJW07]) propose de retourner, pour chaque table, non seulement les données de la même page que la requête mais aussi un échantillon des données des pages voisines. Le taux d’échantillonnage est plus élevé pour les pages les plus proches. La figure suivante montre quelles pages sont considérées pour une des tables de la figure précédente. A rappel constant, le nombre de tables peut ainsi être réduit d’un ordre de grandeur.

Fig. 41 Multi-probe LSH

Question : Supposons que les données sur lesquelles le hachage est appliqué sont des vecteurs de grande dimension. Parmi les observations suivantes, lesquelles vous semblent correctes ?

1. multi-probe LSH augmente fortement (par rapport au hachage simple) le temps nécessaire pour retourner les données de chaque table car chaque page a de nombreux voisins directs

2. multi-probe LSH permet d’augmenter la précision des requêtes car seules les données des pages voisines sont retournées

3. pour une même valeur de rappel, multi-probe LSH permet d’économiser l’espace de stockage par rapport au hachage simple

LSH pour la distance de Hamming. Dans de nombreux cas, les données (observations) sont décrites par un nombre \(m\) très élevé de variables binaires (vrai/faux, achat/non achat, consultation/non consultation, etc.). Chaque observation est ainsi représentée par un motif binaire de longueur \(m\). Le domaine est alors \(\mathcal{D} \subset \{0,1\}^m\) et la distance entre deux motifs binaires \(\mathbf{x},\mathbf{y} \in \mathcal{D}\) est la distance de Hamming \(d_H(\mathbf{x},\mathbf{y})\), c’est à dire le nombre de positions sur lesquelles \(\mathbf{x}\) et \(\mathbf{y}\) diffèrent.

Les fonctions de hachage élémentaires \(h_i : \mathcal{D} \rightarrow \{0,1\}\), \(h_i(\mathbf{x}) = x_i\) (\(i\)-ème bit de \(\mathbf{x}\), voir la figure suivante) forment une famille de fonctions \((r_1, r_2, p_1, p_2)\)-sensibles. Ces fonctions sont employées pour \(m\) très élevé et un nombre de fonctions de hachage \(n\) comparativement faible dans chaque table de hachage.

\[\begin{split}\begin{array}{l} \phantom{1 1 0 \ldots}\,\,\,\, \downarrow \textrm{position } i\\ 1 1 0 \ldots 0 \,1\, 1 \ldots 0 1 0\\ \underbrace{1 0 0 \ldots 0 \,1\, 0 \ldots 1 0 0}_{m \textrm{ bits}} \end{array}\end{split}\]

Question : Quelle est la distance de Hamming entre 01001100011100001111 et 10110011100011110000 ?

Réponse :

Similarité entre ensembles finis. Dans de nombreux cas, les données (observations) sont des sous-ensembles d’un grand ensemble fini. Par exemple, un texte est un sous-ensemble de l’ensemble des mots d’une langue. Le profil d’achat d’un client est un sous-ensemble de l’ensemble des articles disponibles (dans le présent et le passé). Parfois, les ensembles sont représentés à travers leurs fonctions caractéristiques et comparés grâce à la distance de Hamming (voir ci-dessus). Dans d’autres cas, les occurrences des éléments sont pondérées et les comparaisons font appel à la distance cosinus (nous y reviendrons dans le chapitre suivant). Souvent, les (sous-)ensembles sont comparés directement grâce à l’indice (ou la similarité) de Jaccard.

Considérons un ensemble total \(\mathcal{E}\), le domaine qui nous intéresse est \(\mathcal{D} = \mathcal{P}(\mathcal{E})\), l’ensemble des parties de \(\mathcal{E}\). L’indice de Jaccard entre deux sous-ensembles quelconques \(\mathcal{A},\mathcal{B} \in \mathcal{P}(\mathcal{E})\) est

\[s_J(\mathcal{A},\mathcal{B}) = \frac{|\mathcal{A} \cap \mathcal{B}|}{|\mathcal{A} \cup \mathcal{B}|}\]

c’est à dire le rapport entre le nombre d’éléments communs entre \(\mathcal{A}\) et \(\mathcal{B}\) et le nombre d’éléments de leur réunion. Cet indice varie entre 0 (aucun élément commun) et 1 (\(\mathcal{A} = \mathcal{B}\)). On note que \(d_J(\mathcal{A},\mathcal{B}) = 1 - s_J(\mathcal{A},\mathcal{B})\) est une métrique sur \(\mathcal{P}(\mathcal{E})\).

Question : Quelle est la similarité de Jaccard entre les ensembles \(\{a, b, c, d, e\}\) et \(\{a, c, e, g, i\}\) ?

Réponse :

Des fonctions LSH adaptées aux ensembles peuvent être définies sur la base de cet indice de Jaccard. On fixe un ordre des éléments de \(\mathcal{E}\) et on note par \(\pi\) une permutation des éléments de \(\mathcal{E}\). La figure suivante montre un exemple de permutation pour un ensemble dont les éléments sont notés par \(a, b, c, d\ldots\) :

\[\begin{split}\pi = \Big(\begin{array}{ccccc}a & b & c & d & \ldots\\c & d & a & b & \ldots\end{array}\Big)\end{split}\]

Les fonctions de hachage élémentaires \(h_{\pi} : \mathcal{P}(\mathcal{E}) \rightarrow \mathcal{E}\), \(h_{\pi}(\mathcal{A}) = \min \pi(\mathcal{A})\), forment une famille de fonctions \((r_1, r_2, p_1, p_2)\)-sensibles. Nous avons noté par \(\min \pi(\mathcal{A})\) l’élément de \(\mathcal{A}\) qui se retrouve premier après cette permutation.

Le tableau suivant montre le résultat de la permutation considérée ci-dessus sur trois ensembles \(\mathcal{A}, \mathcal{B}, \mathcal{C}\). Ainsi, \(\min \pi(\mathcal{A}) = c\), \(\min \pi(\mathcal{B}) = c\) et \(\min \pi(\mathcal{C}) = b\).

\[\begin{split}\begin{array}{c|c|c|c||c|c|c|c} \mathcal{E} & \mathcal{A} & \mathcal{B} & \mathcal{C} & \pi(\mathcal{E}) & \pi(\mathcal{A}) & \pi(\mathcal{B}) & \pi(\mathcal{C})\\ \hline a & 1 & 0 & 0 & c & 1 & 1 & 0\\ b & 0 & 0 & 1 & d & 0 & 0 & 0\\ c & 1 & 1 & 0 & a & 1 & 0 & 0\\ d & 0 & 0 & 0 & b & 0 & 0 & 1\\ \ldots & & & & \ldots & & & & \end{array}\end{split}\]

Examinons de plus près la probabilité de collision. Soit \(x\) le nombre d’éléments communs entre \(\mathcal{A}\) et \(\mathcal{B}\), c’est à dire \(|\mathcal{A} \cap \mathcal{B}|\). Soit \(y\) le nombre d’éléments spécifiques à \(\mathcal{A}\) ou à \(\mathcal{B}\), c’est à dire \(|(\mathcal{A}-\mathcal{B}) \cup (\mathcal{B}-\mathcal{A})|\). Alors, l’indice de Jaccard entre \(\mathcal{A}\) et \(\mathcal{B}\) est \(s_J(\mathcal{A},\mathcal{B}) = \frac{x}{x+y}\). Aussi, pour toute fonction \(h_{\pi}\), la probabilité de trouver en premier après la permutation \(\pi\) un élément commun plutôt qu’un élément spécifique est \(\frac{x}{x+y}\). Donc, \(p(h_{\pi}(\mathcal{A}) = h_{\pi}(\mathcal{B})) = \frac{x}{x+y}\). Ainsi, pour toute fonction \(h_{\pi}\) et quels que soient les ensembles \(\mathcal{A},\mathcal{B} \in \mathcal{P}(\mathcal{E})\), la probabilité de collision est égale à l’indice de Jaccard entre les deux ensembles.

Amplification de fonctions LSH

Pour la comparaison des ensembles, examinons l’impact du regroupement de \(n\) fonctions de hachage choisies aléatoirement de façon indépendante ; le hash résultant est la concaténation des hash des fonctions regroupées. Considérons deux ensembles quelconques \(\mathcal{A},\mathcal{B}\), on note par \(s\) l’indice de Jaccard entre les deux ensembles, \(s = s_J(\mathcal{A},\mathcal{B})\). Deux ensembles sont en collision dans la table (ont un même hash résultant) s’ils sont en collision par rapport la première fonction ET par rapport à la deuxième ET … ET par rapport à la dernière, donc par rapport à chacune des \(n\) fonctions indépendantes. La probabilité de collision dans la table est donc \(s^n\) ; comme \(0 \leq s \leq 1\), \(s^n \leq s\).

Intéressons-nous maintenant à l’utilisation de \(t\) tables, obtenues à partir de fonctions élémentaires indépendantes (chaque table à partir de \(n\) fonctions). Deux ensembles \(\mathcal{A},\mathcal{B}\) (d’indice de Jaccard \(s\)) sont en collision par rapport à cet ensemble de tables s’ils sont en collision dans la première OU dans la deuxième OU … OU dans la dernière table, donc dans au moins une des \(t\) tables. Dans chaque table, la probabilité de collision est \(s^n\) (comme montré plus haut). La probabilité de non collision dans une table est alors \(1 - s^n\). Les tables étant indépendantes, la probabilité de non collision dans aucune des \(t\) tables est \((1 - s^n)^t\). En conséquence, la probabilité de collision dans au moins une table est \(1 - (1 - s^n)^t\).

Le graphique suivant montre la probabilité de collision (\(\in (0, 1)\)) en fonction de \(s_J(\mathcal{A},\mathcal{B})\) (\(\in (0, 1)\)) pour l’utilisation de :

1. Une seule fonction élémentaire : \(P_c = s\).

2. Une table constituée de 10 fonctions élémentaires indépendantes : \(P_c = s^{10}\).

3. Cinq tables, chacune constituée de 3 fonctions élémentaires indépendantes : \(P_c = 1 - (1 - s^3)^5\).

4. Cent tables, chacune constituée de 10 fonctions élémentaires indépendantes : \(P_c = 1 - (1 - s^{10})^{100}\).

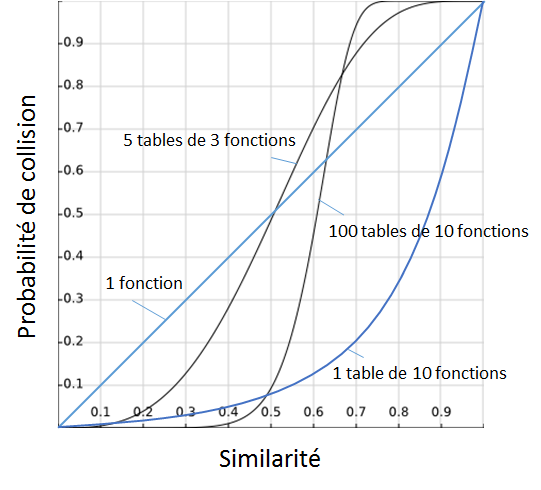
Toutes ces solutions sont \((r_1, r_2, p_1, p_2)\)-sensibles, pour le voir il suffit de fixer \(r_1 < r_2\) et de lire \(p_1 > p_2\) sur la courbe correspondante (noter que \(r\) désigne ici une distance, or si \(s\) est l’indice de Jaccard alors \(r = 1-s\)). En revanche, plus le nombre de fonctions par table (\(n\)) et le nombre de tables (\(t\)) augmente, plus la courbe s’applatit pour \(s\) faible et pour \(s\) élevé, c’est à dire plus la probabilité de collision approche 0 pour les ensembles dissimilaires et 1 pour les ensembles similaires. On tend vers un effet de seuil sur la similarité. Cela a un impact positif à la fois sur

1. la précision des résultats : la probabilité de collision entre données dissimilaires étant proche de 0, les résultats contiendront peu de « faux positifs » (données non similaires à la requête mais retournées) et

2. le rappel : la probabilité de collision entre données similaires étant proche de 1, il y a peu de « faux négatifs » (données similaires à la requête mais non retournées).

Question : Comment procéder pour augmenter le rappel (ou augmenter le pourcentage de données retournées parmi celles similaires à la requête) ?

1. augmenter le nombre de fonctions de hachage (\(n\)) par table de hachage

2. augmenter le nombre de tables de hachage (\(t\))

3. employer une approche multi-probe

4. employer une recherche exhaustive plutôt que LSH

Cette méthode d”« amplification » de fonctions LSH est générale. Considérons une famille de fonctions de hachage \((r_1, r_2, p_1, p_2)\)-sensibles (avec \(r_2 > r_1 > 0\), \(p_1 > p_2 > 0\)), voir la définition dans les équations (1). L’objectif de l’amplification est de rapprocher \(p_2\) (la probabilité de collision entre données dissimilaires) de 0 et \(p_1\) (la probabilité de collision entre données similaires) de 1.

Le regroupement de \(n\) fonctions dans de nouvelles fonctions \(h_{\texttt{AND}}\) (appelées jusqu’ici tables de hachage) revient à faire un ET logique entre les collisions par rapport aux \(n\) fonctions : \(h_{\texttt{AND}}(x) = h_{\texttt{AND}}(y)\) si et seulement si \(h_i(x) = h_i(y)\) pour tout \(i\), \(1 \leq i \leq n\). On constate que ces nouvelles fonctions \(h_{\texttt{AND}}\) sont \((r_1, r_2, p^n_1, p^n_2)\)-sensibles.

Faire la réunion des résultats de \(t\) fonctions revient à un OU logique entre les \(t\) fonctions : \(h_{\texttt{OR}}(x) = h_{\texttt{OR}}(y)\) si et seulement si \(h_i(x) = h_i(y)\) pour au moins une valeur de \(i\), \(1 \leq i \leq n\). Les nouvelles fonctions \(h_{\texttt{OR}}\) sont \((r_1, r_2, 1 - (1 - p_1)^t, 1 - (1 - p_2)^t)\)-sensibles.

Enfin, faire la réunion des résultats de \(t\) fonctions \(h_{\texttt{AND}}\) (c’est à dire la réunion des résultats de plusieurs tables de hachage) engendre de nouvelles fonctions \(h_{\texttt{OR,AND}}\) qui sont \((r_1, r_2, 1 - (1 - p^n_1)^t, 1 - (1 - p^n_2)^t)\)-sensibles.

Comme nous pouvons le constater en examinant la figure précédente, l’amplification de fonctions LSH permet de s’approcher d’une fonction à seuil : les données dont la similarité avec la requête est supérieure au seuil sont presque toujours retournées (car en collision avec la requête) alors que les données dont la similarité avec la requête est inférieure au seuil ne le sont presque jamais. De plus, le « seuil » peut être réglé en modifiant \(n\) (le nombre de fonctions de hachage par table) et \(t\) (le nombre de tables de hachage).

Bien entendu, cela a un coût : l’augmentation de \(n\) mène à une augmentation du temps de recherche (linéaire avec \(n\)), alors que l’augmentation de \(t\) engendre une augmentation (linéaire avec \(t\)) à la fois du temps de recherche et de la place mémoire nécessaire pour le stockage des tables de hachage. Dans la pratique il faut trouver le bon compromis entre la qualité (et la position exacte) du « seuil » obtenu et le coût temporel et spatial (mémoire occupée) de la recherche.

---

[GIM99]

Gionis, A., P. Indyk, R. Motwani. Similarity search in high dimensions via hashing. Dans Proceedings of the 25th International Conference on Very Large Data Bases, VLDB’99, pages 518–529, San Francisco, CA, USA, 1999. Morgan Kaufmann Publishers Inc.

[LJW07]

Lv, Q., W. Josephson, Z. Wang, M. Charikar, K. Li. Multi-probe LSH: Efficient indexing for high-dimensional similarity search. Dans Proceedings of the 33rd International Conference on Very Large Data Bases, VLDB’07, pages 950–961. VLDB Endowment, 2007.

[Sam05]

Samet, H. Foundations of Multidimensional and Metric Data Structures. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 2005.