Travaux pratiques - Analyse d’un grand graphe (Medline)

Cahier Jupyter

Références externes utiles :

• Documentation Spark

• Démarrage avec les DataFrames Spark en Python

• Documentation API Spark en Python

• Tutoriel Spark avec exemples

• Site langage Python

Objectif du TP

Nous allons travailler sur des articles scientifiques, décrits par des mots-clefs (ou tags) et étudier le graphe de ces tags (qui seront reliés si un ou plusieurs articles les possèdent en commun). Notre but sera de comprendre la structure et les propriétés du graphe. Dans cette première partie, nous allons commencer par une analyse simple des sujets principaux des articles et de leurs co-occurrences, ce qui ne nécessitera pas le recours à GraphFrames. On recherchera ensuite les composantes connexes, pour voir si les citations forment des petits groupes ou si, au contraire, elles sont toutes reliées. Nous aborderons ensuite la question de la distribution des degrés dans le graphe.

Description des données

Nous allons récupérer des données textuelles issues d’une base de données de publications scientifiques spécialisées en médecine et sciences du vivant, MEDLINE. Celle-ci est gérée par l’équivalent américain de l’INSERM, la NIH. La base disponible en ligne depuis 1996 et contient plus de 20 millions d’articles. En raison du volume important et de la fréquence élevée des mises à jour, la communauté scientifique a développé un ensemble de tags sémantiques appelé MeSH (Medical Subject Headings), appliqué à toutes les citations de l’index. Ils permettent donc d’étudier les relations entre les documents, afin de faciliter le processus de revue par les pairs et la recherche d’information.

Nous utilisons dans la suite un sous-ensemble des données de citations de MEDLINE et allons étudier le réseau des tags MeSH (restreints à ceux considérés comme « principaux »). Plus précisément, le graphe que nous allons construire aura pour sommets les tags MeSH principaux. On placera une arête entre deux sommets lorsqu’ils seront apparus simultanément comme des tags MeSH principaux dans un même article (on parle de « co-occurence »).

La Fig. 107 illustre la construction de ce graphe. Les mots-clefs en rouge sont les tags MeSH principaux. La présence de « AAA », « BBB » et « CCC » comme tags dans l’article 1 induit la présence de 3 arêtes : (AAA - BBB), (BBB - CCC), (AAA - CCC). Dans cette première partie du TP, on ne tiendra pas compte de la présence de l’arête (BBB - CCC) dans l’article 2 (mais on reviendra sur ce phénomène dans la deuxième partie).

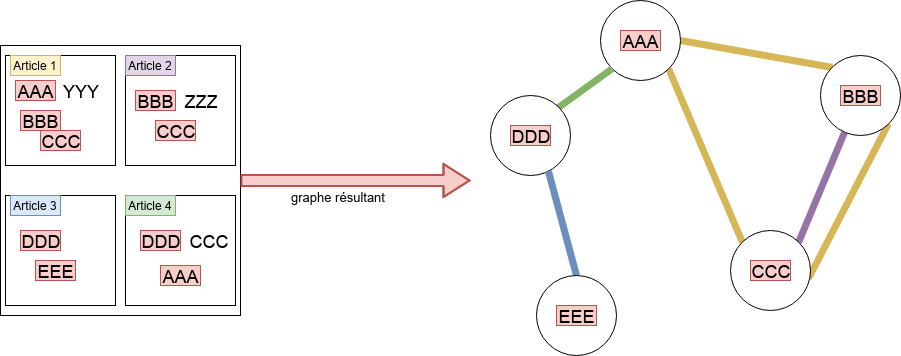
Le graphe support du TP

Démarche générale du TP

Voici les grandes étapes :

• récupération des données (archives, contenant des fichiers XML)

• chargement des données, comme chaînes de caractères, puis XML

• filtrage, extraction des séquences de tags MeSH

• création du RDD de sommets, création du RDD d’arêtes, obtention du graphe

La Fig. 109 illustre les séquences de RDD utilisés dans ces chaînes de traitements (cliquer dessus pour mieux lire les légendes, au besoin).

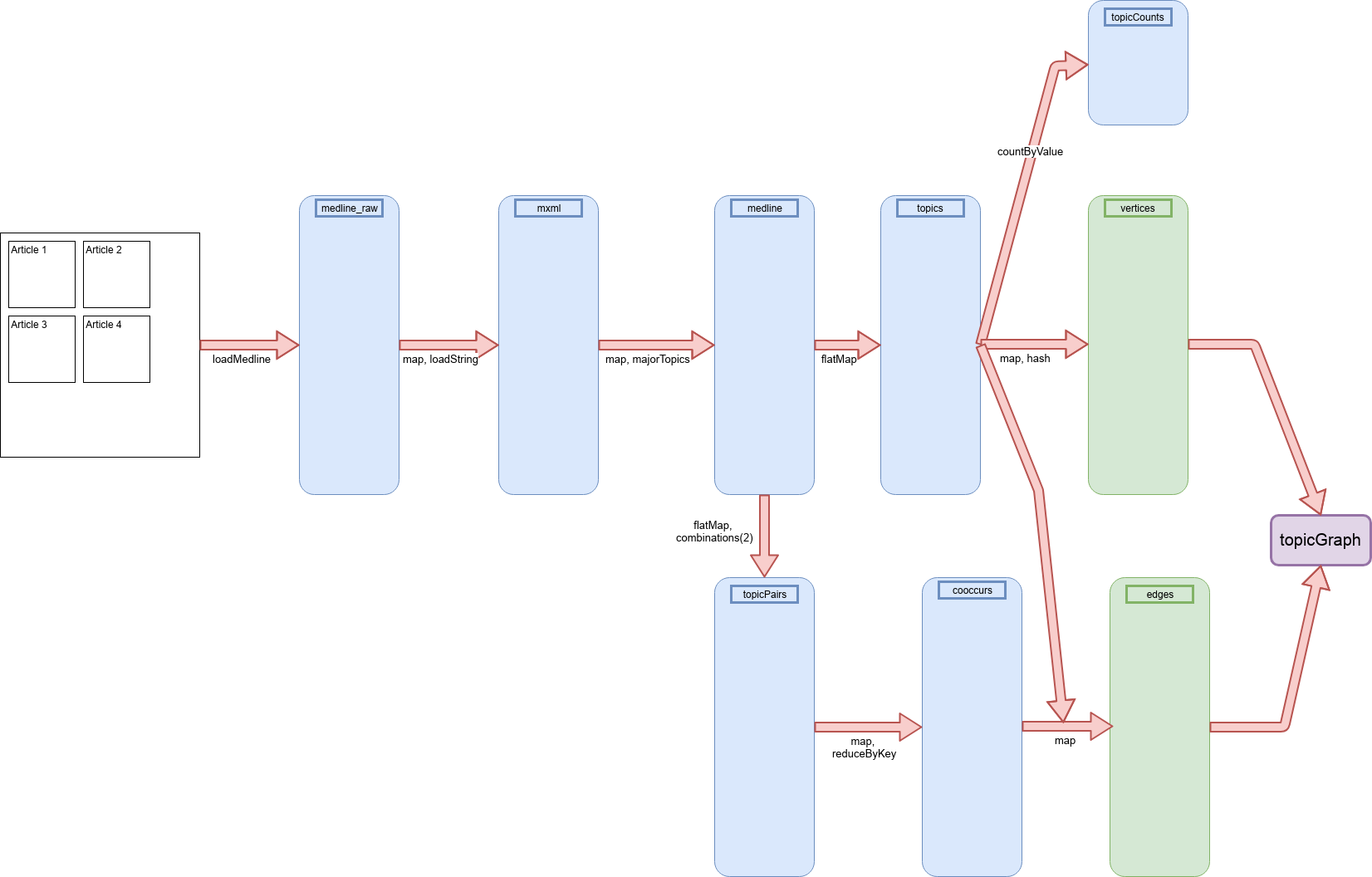
Séquence des RDD utilisés dans le TP

Récupération des données

On va récupérer quelques fichiers contenant des échantillons de l’index des citations sur le serveur FTP du NIH.

# bash
mkdir -p tpgraphes/medline_data
cd tpgraphes/medline_data
wget ftp://ftp.nlm.nih.gov/nlmdata/sample/medline/*.gz

Décompressons les fichiers et regardons leur taille.

# bash
cd tpgraphes/medline_data
gunzip *.gz
ls -ltr

Après décompression, il y a en tout près de 900 Mo de données au format XML. Regardez les données, avec un éditeur de texte (comme kwrite ou gedit par exemple). Chaque entrée est une notice, appelée MedlineCitation, qui contient les informations relatives à la publication de l’article, telles que : le nom du journal, le numéro, la date, les noms des auteurs, et un ensemble de mots-clefs MeSH. Chacun de ces mots a un attribut pour dire s’il s’agit d’un sujet principal (MajorTopic, en anglais) de l’article, ou d’une thématique secondaire. Dans l’exemple ci-dessous, Intelligence n’est pas un majorTopic, à l’inverse de Maternal-Fetal Exchange. Remarquez au passage que nous parlons de « mots-clefs MESH », mais qu’un mot-clef peut être en fait composé de plusieurs termes.

<MedlineCitation Owner="PIP" Status="MEDLINE">
  <PMID Version="1">12255379</PMID>
  <DateCreated>
    <Year>1980</Year>
    <Month>01</Month>
    <Day>03</Day>
  </DateCreated>
  ...
  <MeshHeadingList>
    ...
    <MeshHeading>
      <DescriptorName MajorTopicYN="N">Intelligence</DescriptorName>
    </MeshHeading>
    <MeshHeading>
      <DescriptorName MajorTopicYN="Y">Maternal-Fetal Exchange</DescriptorName>
    </MeshHeading>
    ...
  </MeshHeadingList>
  ...
</MedlineCitation>

Lors du TP sur la fouille de texte, nous étions intéressés à l’étude du texte non structuré. Ici, nous allons examiner les valeurs contenues dans le champ DescriptorName en parsant le XML directement. Scala fournit un très bon support d’XML, nous allons en profiter.

Téléchargez le fichier lsa.jar (créé par mes collègues pour un TP sur la fouille de texte), copiez-le dans le dossier tpgraphes :

# bash
wget http://cedric.cnam.fr/~ferecatu/RCP216/tp/tptexte/lsa.jar -P tpgraphes/jars
wget -nv -nc http://cedric.cnam.fr/vertigo/Cours/RCP216/docs/spark-xml_2.11-0.9.0.jar -P tpgraphes/jars

Avec Spark, on commence par importer les paquetages nécessaires :

import sys
os.environ['PYSPARK_PYTHON'] = sys.executable
os.environ['PYSPARK_DRIVER_PYTHON'] = sys.executable
os.environ['PYSPARK_SUBMIT_ARGS'] = '--jars /home/jovyan/MonDossier/tpgraphes/jars/spark-xml_2.11-0.9.0.jar --packages graphframes:graphframes:0.8.1-spark3.0-s_2.12 pyspark-shell'

from pyspark.conf import SparkConf
from pyspark.sql.session import SparkSession
from pyspark.context import SparkContext
conf = SparkConf().set("spark.jars", "tpgraphes/jars/lsa.jar, tpgraphes/jars/spark-xml_2.11-0.9.0.jar")
sc = SparkContext.getOrCreate(conf=conf)
spark = SparkSession.builder.getOrCreate()

Puis, on crée une fonction chargée d’extraire les entrées dans les fichiers XML contenus dans le dossier medline_data.

Vous devez pour cela utiliser le chemin absolu de ce dossier sur votre machine, que vous pouvez récupérer avec la commande suivante :

# bash
echo ~/tpgraphes/medline_data

Vous devriez pouvoir copier-coller (avec le clic-molette) le chemin obtenu dans l’appel final à loadMedline.

def loadMedline(path):
  temp = sc.newAPIHadoopFile(
      path,
      'com.databricks.spark.xml.XmlInputFormat',
      'org.apache.hadoop.io.LongWritable',
      'org.apache.hadoop.io.Text',
  conf={
      'xmlinput.start':'<MedlineCitation ',
      'xmlinput.end':'</MedlineCitation>',
      'xmlinput.encoding': 'utf-8'})
  #temp.map(lambda l: str(l[1]))
  return temp

rdds = {}
for letter in "abcdefgh":
    rdds[letter] = loadMedline("tpgraphes/medline_data/medsamp2016"+letter+".xml")

medline_raw = rdds["a"].union(rdds["b"]).union(rdds["c"]).union(rdds["d"]).union(rdds["e"]).union(rdds["f"]).union(rdds["g"]).union(rdds["h"])

Regardez ensuite ce que vous avez récupéré dans medline_raw.

# attention, sortie un peu longue
for cit in medline_raw.take(2):
   print(cit[1])
   print('--------------')

Vous pouvez bien sûr utiliser les différentes structures de données pour visualiser certains éléments de ce qui a été récupéré :

medline_raw.take(3)[2][1]

Pour manipuler l’arbre XML, on utilise la bibliothèque ElementTree.

import xml.etree.ElementTree as ET

root = ET.fromstring(medline_raw.take(1)[0][1])
for element in root.iter('DescriptorName'):
   if element.attrib['MajorTopicYN'] == 'Y':
      print(element.text)

def majorTopics(string):
    mtlist = []
    elem = ET.fromstring(string) # devient du XML
    for descriptor in elem.iter('DescriptorName'):
        if descriptor.attrib['MajorTopicYN'] == 'Y':
            mtlist.append(descriptor.text)
    return mtlist

majorTopics(medline_raw.take(3)[2][1])

Créons maintenant le RDD avec tous les sujets.

medline = medline_raw.map(lambda t: majorTopics(t[1]))
medline.take(1)

Comptons le nombre de sujets obtenus. Attention, la cellule peut être longue à exécuter, en raison de l’évaluation paresseuse de Spark.

medline.count()

topics = medline.flatMap(lambda l: l)
topics.take(4)

Co-occurrences des sujets principaux de MeSH

Nous avons maintenant extrait les tags MeSH des données MEDLINE, nous allons commencer par calculer quelques statistiques simples, comme le nombre d’enregistrements et un histogramme des fréquences des sujets principaux.

topicCounts = topics.countByValue()
nbTopics = len(topicCounts)
print("Taille de topicCounts: {taille}".format(taille=nbTopics))

list(sorted(topicCounts.items(), key=lambda item: item[1], reverse=True))[:10]

Nous cherchons ici les co-occurrences des sujets principaux. Chaque entrée de medline est une liste de (chaînes de caractères qui sont les) sujets attribués à chaque article. Il nous faut donc générer tous les sous-ensembles de deux éléments de ces listes. Pour cela, Python nous fournit heureusement une méthode appelée combinations, qui permet d’obtenir le résultat escompté. Voici, sur un exemple simple, comment utiliser cette méthode :

from itertools import combinations

A = [1,2,3]
temp = combinations(A, 2)

for i in list(temp):
    print (i)

print('---')

B = reversed(A)
tempB = combinations(B, 2)

for i in list(tempB):
    print (i)

On doit cependant se méfier : les listes retournées par combinations tiennent compte de l’ordre des éléments, et deux listes comportant les mêmes éléments dans le désordre ne sont pas égales :

list([3, 2]) == list([2, 3])

donne comme résultat False.

Regardons une sortie triée (sorted) de nos données :

a = sorted(medline.take(6)[5])
print(a)

Il faudra donc que l’on s’assure que les listes de sujets sont triées (alphabétiquement) avant d’appeler combinations, d’où le sorted ci-dessous :

topicPairs = medline.flatMap(lambda l: combinations(sorted(l),2))
topicPairs.take(5)

from operator import add
cooccurs = topicPairs.map(lambda p: (p, 1)).reduceByKey(add)
cooccurs.take(10)

cooccurs.cache()
cooccurs.count()

Question :

Quel est le nombre total de co-occurrences possible ? Combien en obtenez-vous ?

Correction :

Le nombre maximal possible de co-occurrences est égal aux combinaisons du nombre total de topic différents (14548, voir len(topicCounts) plus haut) par deux, donc 14547 * 14548/2. On en obtient seulement 213745 (distinctes, voir cooccurs.count()).

Regardons quelles sont les paires les plus fréquentes :

cooccurs.sortBy(lambda x: x[1], ascending=False).collect()[:10]

Construction d’un graphe de co-occurrences avec GraphFrames

Les outils standard d’analyse nous fournissent donc pour l’instant assez peu d’informations sur les relations entre les mots-clefs. Les paires qui apparaissent le plus (ou le moins) fréquemment sont souvent celles qui nous importent le moins. Nous changeons donc maintenant de paradigme et regardons les différents sujets comme les sommets d’un graphe. L’existence d’un article comportant deux sujets nous permettra d’établir une arête entre ces deux sujets. On pourra ainsi calculer des indicateurs reposant sur la structure du graphe et mieux comprendre le réseau de mots-clefs.

On utilise pour cela la bibliothèque GraphFrames.

Un dataframe d’arêtes doit contenir 2 colonnes spéciales, src et dst, pour stocker les identifiants des deux extrémités de chaque arête. Ici les arêtes sont obtenues à partir des co-occurrences de sommets trouvées plus haut (cooccurs) :

from pyspark.sql.types import StructType,StructField, StringType, IntegerType
edges_schema = StructType([
    StructField('src', StringType(), True),
    StructField('dst', StringType(), True),
    StructField('freq', IntegerType(), True)
])
edges = spark.createDataFrame(data = cooccurs.map(lambda l: (l[0][0],l[0][1],l[1])), schema = edges_schema)
edges.printSchema()
edges.show(8,truncate=False) # tout afficher

# vous pouvez n'afficher que les paires
edges.select("src","dst").show(8,truncate=False)

Créons le dataframe de sommets :

tmp_vert = topics.distinct().map(lambda t: (t,(hash(t)) ))
vertices_schema = StructType([
    StructField('id', StringType(), True),
    StructField('hash', StringType(), True),
        ])
vertices = spark.createDataFrame(data = tmp_vert, schema = vertices_schema)
vertices.printSchema()
vertices.show(8,truncate=False) # shows all columns"

Noter que dans topics chaque MajorTopic apparaît autant de fois que dans la collection d’articles, or dans le graphe que nous souhaitons construire un MajorTopic doit correspondre à un seul sommet, d’où l’emploi de .distinct() pour éviter les doublons (cela est par ailleurs cohérent avec les arêtes définies plus haut).

Nous pouvons maintenant créer l’objet GraphFrame que nous préparons depuis le début de la séance :

from graphframes import *
topicGraph = GraphFrame(vertices, edges)

Vérifions que cela fonctionne, en utilisant une méthode affichant les degrés des nœuds.

topicGraph.inDegrees.show()

Nous pouvons aussi vérifier le nombre de sommets :

topicGraph.vertices.count()

Comprendre la structure du graphe

Composantes connexes

Une des choses élémentaires à regarder sur un graphe pour commencer d’en comprendre la structure est sa connexité. Dans un graphe connexe, il est possible d’atteindre un sommet depuis n’importe quel autre en suivant un chemin (une séquence de sommets). Si le graphe n’est pas connexe, il est divisé en plusieurs composantes connexes, des sous-parties du graphes qui sont connexes, que l’on peut examiner individuellement. La connexité étant une propriété importante, GraphFrames fournit une méthode directement.

!mkdir checkpoints
spark.sparkContext.setCheckpointDir('checkpoints')

# calcul des composantes connexes du graphe
topicCC = topicGraph.connectedComponents()

Le dataframe topicCC contient les identifiants des sommets du graphe, un hash et la composante connexe à laquelle ils appartiennent.

La méthode suivante permet de les trier par taille, mais elle peut échouer, compte tenu de sa complexité et de la taille des structures manipulées.

from pyspark.sql import functions as F

(topicCC.sort("component")
       .groupby("component")
       .agg(F.collect_list("id").alias("libraries"))
       .show(8,truncate=False))

Pour compter le nombre de composantes connexes puis afficher la taille des 10 composantes connexes les plus grandes, on peut repasser aux RDD :

topicCCrdd = topicCC.select('component').rdd
from pyspark.sql import Row
temp = topicCCrdd.map(lambda row: row['component'])
cc = temp.countByValue()

cc_sorted = sorted(cc.items(), key=lambda item: item[1], reverse=True)
for k,v in enumerate(cc_sorted[:60]):
    print("Rang", k+1, ": composante connexe", v[0], "nb noeuds:", v[1])

Question :

Qu’observez-vous ?

Correction :

On observe une composante connexe géante, suivie par d’autres composantes connexes bien plus petites et enfin des nœuds isolés.

Question :

Affichez les sommets (nœuds) des composantes connexes des rangs 2 à 10 (la composante de rang 1 est trop grande pour l’afficher en entier).

Correction :

for k,v in enumerate(cc_sorted[1:10]):
    print("Rang", k+1, ": composante connexe", v[0], "nb noeuds:", v[1])
    print(topicCC.filter(topicCC.component==v[0]).select(topicCC.id).show(5,False))

Distribution de degrés

Un graphe connecté peut prendre des formes multiples (étoile, boucle géante). On essaie d’aller plus loin sur la compréhension du réseau de MajorTopic en examinant la distribution de degrés, c’est-à-dire le nombre de sommets qui sont de degré \(n\).

degrees = topicGraph.degrees
degrees.describe('degree').show()

Question :

Commentez les résultats.

Correction :

La moyenne des degrés est très faible par rapport au degré maximal et deux fois inférieure à l’écart-type de la distribution des degrés.

Question :

Il y a une différence entre le count obtenu ici dans summary et le nombre de sommets calculé auparavant, pourquoi ?

Correction :

Certains nœuds ne sont pas connectés à d’autres, ils n’ont qu’un seul sujet majeur, donc pas de co-occurrence avec d’autres.

# quels MajorTopic apparaissent seuls ?
sing = medline.filter(lambda x: len(x) == 1)
sing_topic = sing.flatMap(lambda x: x).distinct()
# combien de MajorTopic apparaissent seuls dans au moins un article ?
print(sing_topic.count())
# quels MajorTopic sont liés à un autre ?
topic2 = topicPairs.flatMap(lambda x: x)
# combien des MajorTopic apparaissant seuls dans au moins un article
#  ne sont pas liés à d'autres MajorTopic dans d'autres articles ?
sing_topic.subtract(topic2).count()

On retrouve bien 13721 + 827 = 14548 nœuds dans le graphe.

Nœuds de fort degré

Il y a des nœuds de fort degré, on se donne la méthode suivante pour trouver leurs noms :

d = degrees.select("degree").rdd.flatMap(lambda x:x)
freqDegres = d.countByValue()
# on obtient le nombre de sommets de degrés n
distribDegres = sorted(freqDegres.items(), key=lambda item: item[0], reverse=True)

print("degré","nb_sommets")
for k,v in enumerate(distribDegres[:10]):
    print(v[0],v[1])

Et l’on peut afficher les 10 sommets de plus fort degré ainsi :

from pyspark.sql.functions import *
topicGraph.degrees.orderBy('degree', ascending=False).show(10)

Vous devriez constater qu’on retrouve les termes les plus fréquents, qui sont donc aussi les plus connectés. On pourrait ensuite filtrer ces nœuds de très fort degré (connectés à tout le monde, ils n’apportent que peu d’information), et observer si la structure du graphe reste la même, si la composante connexe géante se désagrège petit à petit, ou s’il y a un moment où l’on a enlevé suffisamment de nœuds et la structure actuelle disparaît.

Bibliographie

Karau, H., A. Konwinski, P. Wendell et M. Zaharia, Learning Spark, O’Reilly, 2015.

Ryza, S., U. Laserson, S. Owen and J. Wills, Advanced Analytics with Spark, O’Reilly, 2010.

Large-Scale Structure of a Network of Co-Occurring MeSH Terms: Statistical Analysis of Macroscopic Properties, by Kastrin et al. (2014),