Travaux pratiques - Deep Learning avec Keras

Cahier Jupyter

L’objectif de cette seconde séance de travaux pratiques est de prendre en main la librairie Keras https://keras.io/ pour utiliser et entraîner des réseaux de neurones profonds.

Avec Keras, les réseaux de neurones avec une structure de chaîne (réseaux feedforward), s’utilisent de la manière suivante:

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import Sequential
model = Sequential()

On crée ainsi un réseau de neurones vide. On peut alors ajouter des couches avec la fonction add.

Exercice 1 : Régression Logistique avec Keras

Par exemple, l’ajout d’une couche de projection linéaire (couche complètement connectée) de taille 10, suivi de l’ajout d’une couche d’activation de type softmax, peuvent s’effectuer de la manière suivante :

from tensorflow.keras.layers import Dense, Activation
model.add(Dense(10,  input_dim=784, name='fc1'))
model.add(Activation('softmax'))

On peut ensuite visualiser l’architecture du réseau avec la méthode summary() du modèle.

model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
fc1 (Dense)                  (None, 10)                7850
_________________________________________________________________
activation (Activation)      (None, 10)                0
=================================================================
Total params: 7,850
Trainable params: 7,850
Non-trainable params: 0
_________________________________________________________________

Question :

Quel modèle de prédiction reconnaissez-vous ? Vérifier le nombre de paramètres du réseau à apprendre dans la méthode summary().

Avec Keras, on va compiler le modèle en lui passant un loss (ici l’entropie croisée), une méthode d’optimisation (ici une descente de gradient stochastique, stochastic gradient descent, sgd), et une métrique d’évaluation (ici le taux de bonne prédiction des catégories, accuracy):

optimizer = keras.optimizers.SGD(learning_rate=0.5)
model.compile(loss='categorical_crossentropy',optimizer=optimizer,metrics=['accuracy'])

Enfin, l’apprentissage du modèle sur des données d’apprentissage est mis en place avec la méthode fit :

batch_size = 300
nb_epoch = 10
# convert class vectors to binary class matrices
(X_train, y_train), (X_test, y_test) = keras.datasets.mnist.load_data()
# One-hot encoding
Y_train = keras.utils.to_categorical(y_train, 10)
Y_test = keras.utils.to_categorical(y_test, 10)
#  Reshape each 28x28 image -> 784 dim. vector
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
# Normalization
X_train /= 255
X_test /= 255

model.fit(X_train, Y_train,batch_size=batch_size, epochs=nb_epoch,verbose=1)

• batch_size correspond au nombre d’exemples utilisé pour estimer le gradient de la fonction de coût.

• epochs est le nombre d’époques (i.e. passages sur l’ensemble des exemples de la base d’apprentissage) lors de la descente de gradient.

N.B : on rappelle que comme dans les TME précédents, les étiquettes (labels) données par la supervision doivent être au format one-hot encoding.

On peut ensuite évaluer les performances du modèle sur l’ensemble de test avec la fonction evaluate :

scores = model.evaluate(X_test, Y_test, verbose=0)
print("%s: %.2f%%" % (model.metrics_names[0], scores[0]*100))
print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))

Le premier élément de scores renvoie la fonction de coût sur la base de test, le second élément renvoie le taux de bonne détection (accuracy).

• Implémenter l’apprentissage du modèle sur la base de train de la base MNIST.

• Évaluer les performances du réseau sur la base de test et les comparer à celles obtenues lors du TME 1. Conclure.

Exercice 2 : Perceptron avec Keras

On va maintenant enrichir le modèle de régression logistique en insérant une couche de neurones cachés complètement connectée (suivie d’une fonction d’activation non linéaire de type sigmoïde) entre la couche d’entrée et la couche de sortie. On va ainsi obtenir un réseau de neurones à une couche cachée, le Perceptron (cf. TP2).

• Écrire un script exo2.py pour mettre en place le Perceptron.

La première couche de ce réseau peut être obtenue de la manière suivante en Keras :

• Sur un réseau séquentiel vide, on va ajouter la méthode add pour insérer une couche cachée (de taille 100):

model.add(layers.Dense(100, name='fc2'))

• La non-linéarité de type sigmoïde sera obtenue de la manière suivante :

model.add(Activation('sigmoid'))

• Créer un nouveau modèle en ajoutant la couche de sortie à 10 classes suivie de la fonction d’activation soft-max. On retrouve ainsi le Multi-Layer Perceptron du TP précédent.

• Quel est maintenant le nombre de paramètres du modèle MLP ? Justifier le calcul et le vérifier avec la méthode summary().

model = ... # À compléter
model.add(...) # À compléter
#...

model.summary()

Model: "sequential_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
fc1 (Dense)                  (None, 10)                7850
_________________________________________________________________
activation_1 (Activation)    (None, 10)                0
_________________________________________________________________
fc2 (Dense)                  (None, 100)               1100
_________________________________________________________________
activation_2 (Activation)    (None, 100)               0
=================================================================
Total params: 8,950
Trainable params: 8,950
Non-trainable params: 0
_________________________________________________________________

Une fois le modèle MLP créé, la façon de l’entraîner est strictement identique à ce qui a été écrit dans l’exercice précédent, l’algorithme de rétro-propagation du gradient de l’erreur permettant de mettre à jour l’ensemble des paramètres du réseau.

• Effectuer l’entraînement du réseau MLP.

• Évaluer les performances du réseau sur la base de test et les comparer à celles obtenues lors du TME 2. Conclure.

• Observer la documentation Keras pour voir la façon dont les paramètres du modèles sont initialisés dans les différentes couches.

#Compiler le modèle avec .compile()

#Effecturer l'entraînement avec .fit()

• On pourra utiliser la méthode suivante pour sauvegarder le modèle appris :

model.save('MLP.h5')

Pour charger votre modèle sauvegardé :

# from tensorflow.keras.models import load_model
# model = load_model('MLP.h5')

Exercice 3 : Réseaux de neurones convolutifs avec Keras

On va maintenant étendre le perceptron de l’exercice précédent pour mettre en place un réseau de neurones convolutif profond, Convolutional Neural Networks, ConvNets.

Mise en place d’un ConvNet.

Les réseaux convolutifs manipulent des images multi-dimensionnelles en entrée (tenseurs). On va donc commencer par reformater les données d’entrée afin que chaque exemple soit de taille \(28\times 28\times 1\).

X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
input_shape = (28, 28, 1)

Par rapport aux réseaux complètement connectés, les réseaux convolutifs utilisent les briques élémentaires suivantes :

1. Des couches de convolution, qui transforment un tenseur d’entrée de taille \(n_x \times n_y \times p\) en un tenseur de sortie \(n_{x'} \times n_{y'} \times n_H\), où \(n_H\) est le nombre de filtres choisi.

Par exemple, une couche de convolution pour traiter les images d’entrée de MNIST peut être créée de la manière suivante :

from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Conv2D, MaxPooling2D
Conv2D(32,kernel_size=(5, 5),activation='sigmoid',input_shape=(28, 28, 1),padding='same')

• 32 est le nombre de filtres.

• (5, 5) est la taille spatiale de chaque filtre (masque de convolution).

• padding='same' correspond à garder la même taille spatiale en sortie de la convolution.

• N.B. : on peut directement inclure dans la couche de convolution la non-linéarité en sortie de la convolution, comme illustré ici dans l’exemple avec une fonction d’activation de type sigmoid.

1. Des couches d’agrégation spatiale (pooling), afin de permettre une invariance aux translations locales. Voici par exemple la manière de déclarer une couche de max-pooling:

pool = MaxPooling2D(pool_size=(2, 2))

• (2, 2) est la taille spatiale sur laquelle l’opération d’agrégation est effectuée.

• N.B. : par défaut, le pooling est effectué avec un décalage de 2 neurones, dans l’exemple précédent on obtient donc des cartes de sorties avec des tailles spatiales divisées par deux par rapport à la taille d’entrée.

Mettre en place un ConvNet à l’architecture suivante, proche du modèle historique LeNet5 [LBD+89] et montré ci-dessous:

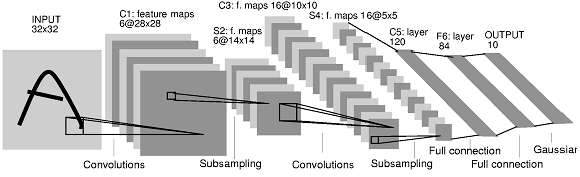
• Une couche de convolution avec 32 filtres de taille \(5 \times 5\), suivie d’une non linéarité de type sigmoïde puis d’une couche de max pooling de taille \(2 \times 2\).

• Une seconde couche de convolution avec 64 filtres de taille \(5 \times 5\), suivie d’une non linéarité de type sigmoïde puis d’une couche de max pooling de taille \(2 \times 2\).

• Comme dans le réseau LeNet, on considérera la sortie du second bloc convolutif comme un vecteur, ce que revient à « mettre à plat » les couches convolutives précédentes (model.add(Flatten())).

• Une couche complètement connectée de taille 100, suivie d’une non linéarité de type sigmoïde.

• Une couche complètement connectée de taille 10, suivie d’une non linéarité de type softmax.

• Apprendre le modèle et évaluer les performances du réseau sur la base de test. Vous devez obtenir un score de l’ordre de 99% pour ce modèle ConvNet.

Apprentissage sur GPU

• Quelle est le temps d’une époque avec ce modèle convolutif ?

• Vous pourrez tester l’apprentissage sur carte graphique du modèle, et comparer le temps d’entraînement

[LBD+89] Yann LeCun, Bernhard Boser, John S Denker, Donnie Henderson, Richard E Howard, Wayne Hubbard, and Lawrence D Jackel. Backpropagation applied to handwritten zip code recognition. Neural computation, 1(4):541–551, 1989.

nb_classes = 10
model = Sequential()
model.add(...) # À compléter
# ...

model.save('LeNet.h5')