Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.

Cours - Méthodes à noyaux

« Statistics is the grammar of science. »

(Karl Pearson)

[Diapositives du cours]

Objectifs et contenu de cette séance de cours

Dans cette séance nous présentons les méthodes à noyaux, une classe de méthodes qui permettent à partir d’un algorithme linéaire d’obtenir une version non linéaire. Le principe est d’appliquer l’algorithme linéaire sur une projection des données dans un espace de dimension (en général) plus grande. Dans certaines conditions, précisées dans la suite, l’existence de cette projection est garantie sans pour autant avoir besoin de l’expliciter. Les résultats de l’analyse linéaire effectuée sur les données projetées peuvent être « rapatriés » dans l’espace initial (dit « espace de départ ») grâce à des entités appelées « fonctions noyaux », obtenant ainsi une version non-linéaire de l’algorithme initial. Les noyaux garantissent le bon fonctionnent d’un ensemble de caractéristiques mathématiques, appellées « le truc à noyaux » (kernel trick en anglais) qui permet de calculer le produit scalaire entre les projections de deux vecteurs via une fonction noyau, sans connaître la forme spécifique de la projection.

Qu’est-ce qu’un noyau ?

Avant de donner une définition formelle on se pose la question : à quoi devrait ressembler une fonction noyau ? Intuitivement, elle est proche d’une mesure de similarité. Plus précisément, si \(x\) et \(y\) sont deux vecteurs, alors un noyau défini pour ces vecteurs doit avoir des valeurs élevées si \(x \approx y\) et des valeurs faibles si \(x\) et \(y\) sont très différents.

Définition. Une fonction \(s:\mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}\) est une mesure de similarité si les conditions suivantes sont satisfaites :

• \(x, y \in \mathcal{X}\;\;\; s(x, y) \geq 0\) (positivité),

• \(x, y \in \mathcal{X}\;\;\; s(x, y) = s(y, x)\) (symétrie),

• \(\forall y \in \mathcal{X}, y\neq x\;\;\;\; s(x, y) < s(x, x)\) (uniformité),

• \(s(x, y) = s(x, x) \Leftrightarrow x = y\) (identité).

A comparer avec la distance \(d(x, y\), qui a des valeurs élevées si \(x\) et \(y\) sont très différents et des valeurs faibles si \(x\) et \(y\) sont proches. Cette intuition concernant la notion de similarité correspond à ce qu’on connaît du produit scalaire : deux vecteurs proches (directions presque parallèles) ont une valeur élevée pour le produit scalaire. Par contre, pour deux vecteurs très différents (orthogonaux) le produit scalaire est proche de zéro.

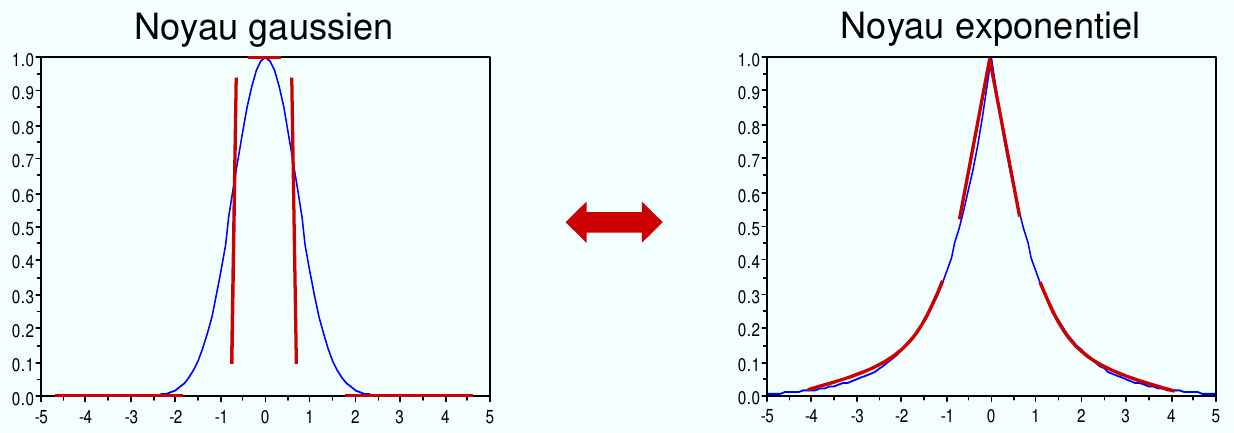
Fig. 50 Exemples de noyaux de forme \(k(x, y) = k(||x-y||)\). Sur l’axe horizontal on représente \(||x-y||\).

Maintenant on présente le résultat fondamental qui permet la définition formelle des fonctions noyau.

Noyau positif défini

Théorème de Mercer

Soit \(\mathcal{X}\) un compact dans \(R^d\) (compact = fermé et borné) et \(K:\mathcal{X}\times \mathcal{X} \rightarrow R\) une fonction symétrique (c.t.d. \(k(x,y) = k(y,x)\)). On suppose aussi que \(\forall f\in L_2(\mathcal{X})\) :

\[\int_{\mathcal{X}}K(x, y)f(x)f(y)dx dy \geq 0 \;\;\; \mathrm{(condition\; de\; Mercer)} \]

Alors il existe un espace de Hilbert \(\mathcal{H}\) et \(\phi:\mathcal{X}\rightarrow \mathcal{H}\) tel que \(\forall x, y \in \mathcal{X}\) :

\[K(x,y) = \langle\phi(x), \phi(y)\rangle\; \mathrm{(produit\; scalaire)} \]

La fonction \(K(x,y)\) s’appelle noyau positif défini.

Une condition équivalente pour que la fonction \(K:\mathcal{X}\times \mathcal{X} \rightarrow R\) soit un noyau positif défini est la suivante :

• \(\forall n \in N\) et \(\{x_i\}_{i=1,\dots, n} \subset \mathcal{X}\) la matrice de Gramm

  \[K = [K_{i,j}]_{i=1,\dots, n} = [K(x_i, x_j)]_{i=1,\dots, n} \]

est définie positive, c’est à dire :

\[\forall c \in R^n, c\neq 0, \mathrm{\;on\;a\;} c^TKc > 0 \]

Un noyau valide garantit donc l’existence de \(\mathcal{H}\) et peut s’exprimer alors comme un produit scalaire dans \(\mathcal{H}\). Un noyau valide garantit aussi la convexité du problème d’optimisation quadratique sous contraintes d’inégalités rencontré pour les SVM, comme nous le verrons plus tard.

Noyau conditionnellement positif défini

Un noyau est conditionnellement défini positif (CDP) si \(\forall n \in N\) et \(\{x_i\}_{i=1,\dots, n} \subset \mathcal{X}\) la matrice de Gramm

\[K = [K_{i,j}]_{i=1,\dots, n} = [K(x_i, x_j)]_{i=1,\dots, n} \]

est conditionnellement définie positive, c’est à dire

\[\forall c \in R^n, c\neq 0 \mathrm{\;tel\;que\;} \sum_{i=1}^{n}c_i = 0 , \mathrm{\;on\;a\;} c^TKc > 0 \]

Cette définition permet d’étendre la classe des fonctions noyaux pour lesquelles le problème d’optimisation SVM (qui sera présenté plus tard) est garanti convexe.

Étant donné un noyau symétrique conditionnellement défini positif, il existe

• un espace vectoriel \(\mathcal{V}\) ;

• une transformation \(\phi: \mathcal{X} \rightarrow \mathcal{V}\) ;

• une forme bilinéaire \(Q:\mathcal{V}\times\mathcal{V}\rightarrow R\)

Tel que :

\[K(x, y) = Q(\phi(x), \phi(y)) \]

• Si \(K\) n’est pas défini positif alors \(Q\) n’est pas un produit scalaire ;

• Un noyau CDP peut être utilisé pour les SVM en discrimination car les contraintes du problème d’optimisation quadratique incluent la condition \(\sum_{i=1}^{n}\alpha_i y_i = 0\) (\(c_i = \alpha_i y_i\)), voir plus loin la présentation des SVM à noyaux.

Construction des noyaux définis positifs

Maintenant on se pose la question comment obtenir des fonctions noyau. Il existe plusieurs approches :

• construction directe (en utilisant la projection \(\phi\) ),

• transformation des noyaux existants,

• combinaison des noyaux existants.

Construction directe

Définition directe de \(\mathcal{H}, \phi:\mathcal{X}\rightarrow\mathcal{H}\) et ensuite construction du noyau

\[K:\mathcal{X}\times\mathcal{X}\rightarrow R \mathrm{\;par\;} K(x,y) = \langle\phi(x), \phi(y)\rangle\; \mathrm{(produit\; scalaire)} \]

Exemple :

• Soit \(\mathcal{X}\) un compact dans \(R\). On prend \(\phi:\mathcal{X}\rightarrow R\), alors \(K:\mathcal{X}\times \mathcal{X}\rightarrow R\) donné par :

\[K(x,y) = \phi(x)\cdot \phi(y)\]

est un noyaux défini positif (appelé « noyau conforme »).

Attention, ces noyaux conformes ne peuvent pas être interprétés comme des similarités.

Cas particuliers :

• \(f:R\rightarrow R, \phi(x) = x : K(x, y) = x\cdot y\) (dit « noyau linéaire »),

• \(f:R\rightarrow R, \phi(x) = e^x, K(x, y) = e^{x+y}\).

Transformation des noyaux

1. Si \(K:\mathcal{X}\times\mathcal{X}\rightarrow R\) est défini positif alors \(exp(K)\) est défini positif aussi.

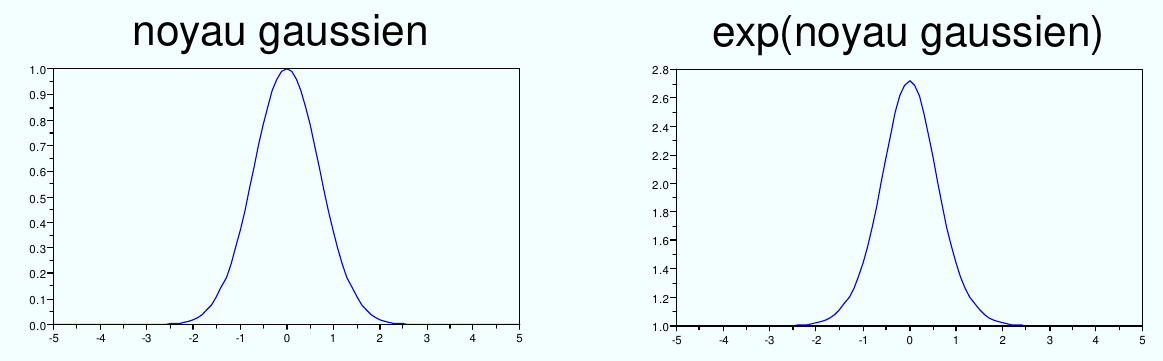
Fig. 51 L’exponentielle d’un noyau est un noyau.

2. Si \(K:\mathcal{X}\times\mathcal{X}\rightarrow [-1, 1]\) est défini positif alors \(\cosh(K)\) est défini positif aussi.

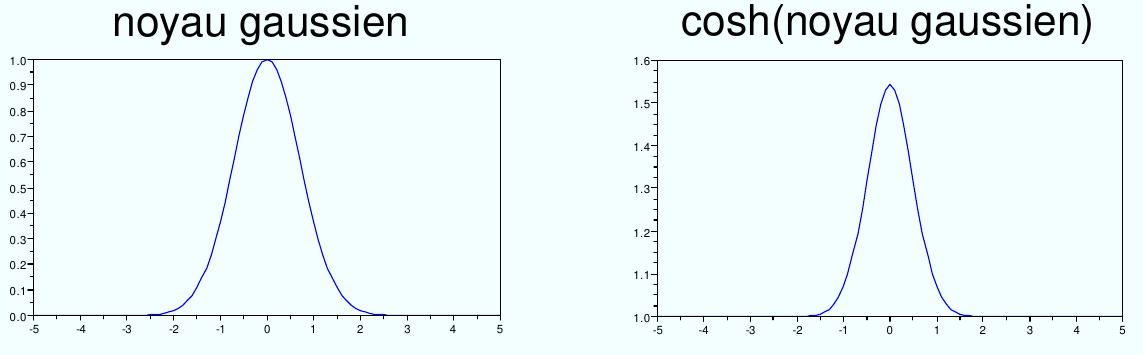
Fig. 52 Le \(\cosh\) d’un noyau est un noyau.

Combiner des noyaux définis positifs

Si \(K_1, K_2:\mathcal{X}\times\mathcal{X}\rightarrow R\) sont définis positifs et \(\alpha_1, \alpha_2 > 0\) alors sont également définis positifs les noyaux suivants :

• la combinaison linéaire : \(K(x, y) = \alpha_1 K_1(x,y) + \alpha_2 K_2(x,y)\),

• le produit simple : \(K(x, y) = \alpha_1 K_1(x,y) \cdot \alpha_2 K_2(x,y)\).

Évidemment, \(K\) est défini sur \(\mathcal{X}\times\mathcal{X}\) à valeurs dans \(\mathbb{R}\).

Si \(K_1:\mathcal{X}_1\times\mathcal{X}_1\rightarrow \mathbb{R}\) et \(K_2:\mathcal{X}_2\times\mathcal{X}_2\rightarrow \mathbb{R}\) sont définis positifs alors sont également défini positifs :

• la somme directe : \(K_1\oplus K_2 = K_1 + K_2\),

• le produit tensoriel : \(K_1\otimes K_2 = K_1 \cdot K_2\).

Noyaux hybrides

Souvent, dans les applications, l’espace \(\mathcal{X}\) n’est pas une partie partie de \(\mathbb{R}^d\). Les éléments de l’espace sont plus complexes, par exemple ils représentent une partie du web, des graphes, des réseaux moléculaires, ADN, protéines, une hiérarchie issue d’un ensemble de motifs (patterns) identifiés par une caméra vidéo. Dans ces cas, une partie importante du travail est de construire un noyau valide pour ce type de données et démontrer qu’il est défini positif, faute de quoi nous n’avons pas la garantie que les algorithmes fonctionnent correctement.

Comme un exemple, on présente dans cette partie les noyaux d’appariement intermédiaire (issus de [Bou05]). Les données sont des ensembles de descripteurs locaux d’images (dans ce cas de points d’intérêt SIFT ). Le détecteur SIFT est appliqué sur chaque image et il détecte un nombre variable de points, qui dépend du contenu de l’image et des conditions de prise de vue. Un point SIFT représente un site « intéressant » d’une image, situé à un endroit où il y a beaucoup de variabilité. Ils sont détectés en général dans les coins et sur les contours (très peu sur des régions uniformes).

Fig. 53 Points SIFT détectés sur une image (source: Wikipedia).

Chaque élément \(\mathcal{E} \in \mathcal{X}\) est donné par l’ensemble de points détectés dans une image (le nombre de points est différent pour chaque image). Pour chaque point, le détecteur SIFT calcule un descripteur de forme de dimension \(d=128\) dans le voisinage du point.

Donc l’espace \(\mathcal{X}\) est ensemble des parties finies mais de cardinalité variable de \(\mathbb{R}^d\) :

\[\mathcal{X} = \mathcal{P}_f(\mathbb{R}^d)\]

L’objectif est évaluer la similarité entre ensembles de vecteurs \(\mathcal{E},\mathcal{E'} \in \mathcal{P}_f(\mathbb{R}^d)\) à travers les proximités entre vecteurs similaires de \(\mathcal{E},\mathcal{E'}\) (noyaux d’appariement intermédiaire).

Le problème est que le noyau d’appariement direct :

\[K(\mathcal{E},\mathcal{E'}) = \frac{1}{2}\left[ \sum_{x_i\in\mathcal{E}}\max_{x'_j\in\mathcal{E'}}K(x_i, x'_j) + \sum_{x'_j\in\mathcal{E'}}\max_{x_i\in\mathcal{E}}K(x'_j, x_i)\right]\]

où \(K(x_i, x'_j)\) est un noyau classique entre les vecteurs \(x_i\) et \(x'_j\), n’est pas défini positif !

Principe du noyau d’appariement intermédiaire : faire l’appariement par rapport à des vecteurs pivots, fixés pour un ensemble d’apprentissage donné (ne dépendant donc pas de \(\mathcal{E}\) et \(\mathcal{E'}\).

Soit \(m\) vecteurs pivot \(p_1, \dots, p_m \in \mathbb{R}^d\). Pour chaque vecteur \(p_l\) on défini une fonction \(\psi_l:\mathcal{X} \rightarrow \mathbb{R}^d, \psi_l(\mathcal{E}) = x^*_l = \operatorname*{arg\,min}_{x\in \mathcal{E}}||x-p_l||\).

Le noyau d’appariement intermédiaire construit à partir des pivots \(p_1, \dots, p_m\) est défini par :

\[K_M(\mathcal{E},\mathcal{E'}) = \sum_{l=1}^{m} K(x_l, x'_l)\]

On peut montrer que ce noyaux est positif défini (voir [Bou05]).

Un choix possible des vecteurs pivots est les prototypes des groupes de vecteurs obtenus par classification automatique des données d’apprentissage.

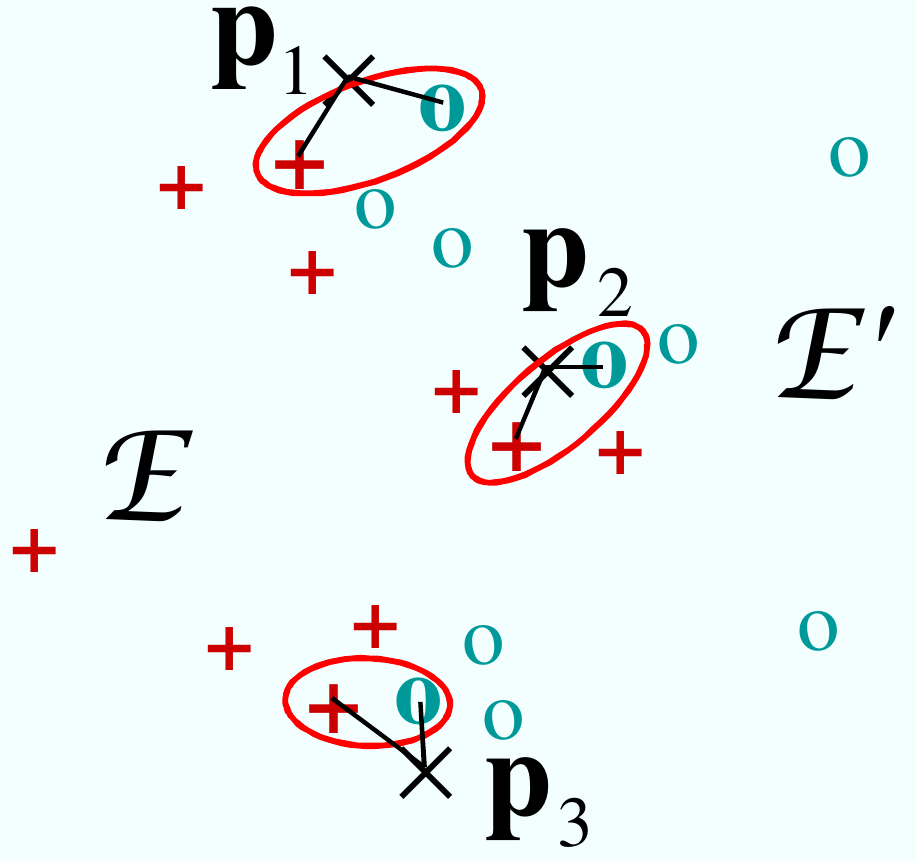
Fig. 54 Calcul du noyau d’appariement intermédiaire : c’est la somme des noyaux élémentaires calculés sur les éléments les plus proches de chaque vecteur pivot.

L’astuce à noyaux

Les SVM (linéaires) sont des séparateurs linéaires qui ont été beaucoup étudiés. Parmi leurs avantages on compte : problème d’optimisation convexe (donc optimum global garanti), il existe des implémentations très efficaces, etc. On se pose donc la question d’étendre ces résultats à des séparateurs non linéaires.

Principe : transposer les données dans un autre espace (en général de plus grande dimension) dans lequel elles sont linéairement séparables (ou presque) et ensuite appliquer l’algorithme SVM sur les données transposées.

Par la théorème de Mercer, si \(K\) est un noyau défini positif (\(K:\mathbb{R}^d \times \mathbb{R}^d \rightarrow \mathbb{R}\)), alors il existe une transformation \(\phi:\mathbb{R}^d\rightarrow \mathcal{H}, x\rightarrow \phi(x)\), vers \(\mathcal{H}\) espace de Hilbert, et :

\[K(x,y) = \langle\phi(x), \phi(y)\rangle \]

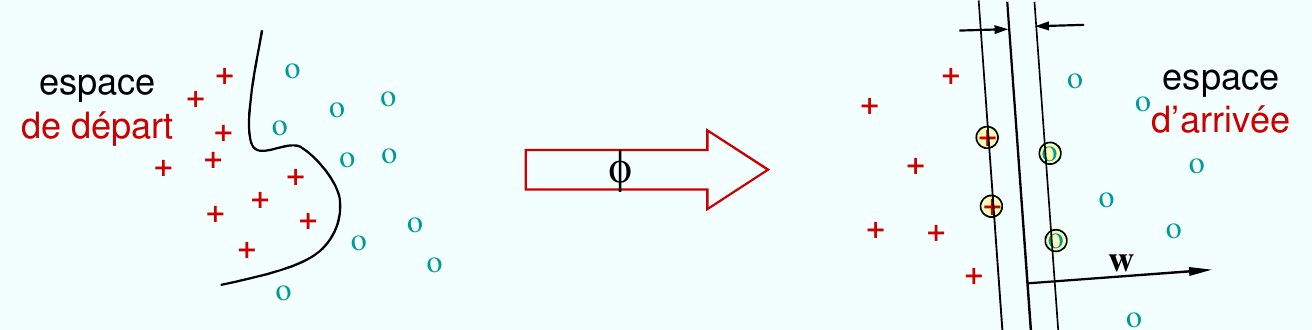
Fig. 55 Astuce à noyaux : projeter les données dans un espace de dimension beaucoup plus grande, où elles deviennent séparables linéairement.

Caractéristiques de l’astuce des noyaux :

• Nous n’avons pas besoin de trouver la fonction \(\phi\).

• Tout algorithme qui utilise seulement des produits scalaires entres les échantillons de données peut tout de suite être appliqué dans l’espace \(\mathcal{H}\), car le produit scalaire dans cet espace se calcule directement via le noyau \(K(x,y) = \langle\phi(x), \phi(y)\rangle\), sans avoir besoin d’expliciter la projection.

Exemples de noyaux

Voici quelques exemples de noyaux, beaucoup utilisés dans les applications. Dans la suite \(x_i, x_j\) sont des vecteurs en \(\mathbb{R}^d\).

• Noyaux linéaire : \(K(x_i, x_j) = x_i^T x_j = \langle x_i, x_j \rangle\)

• Noyau exponentiel : \(K(x_i, x_j) = \exp(-\gamma ||x_i-x_j||)\)

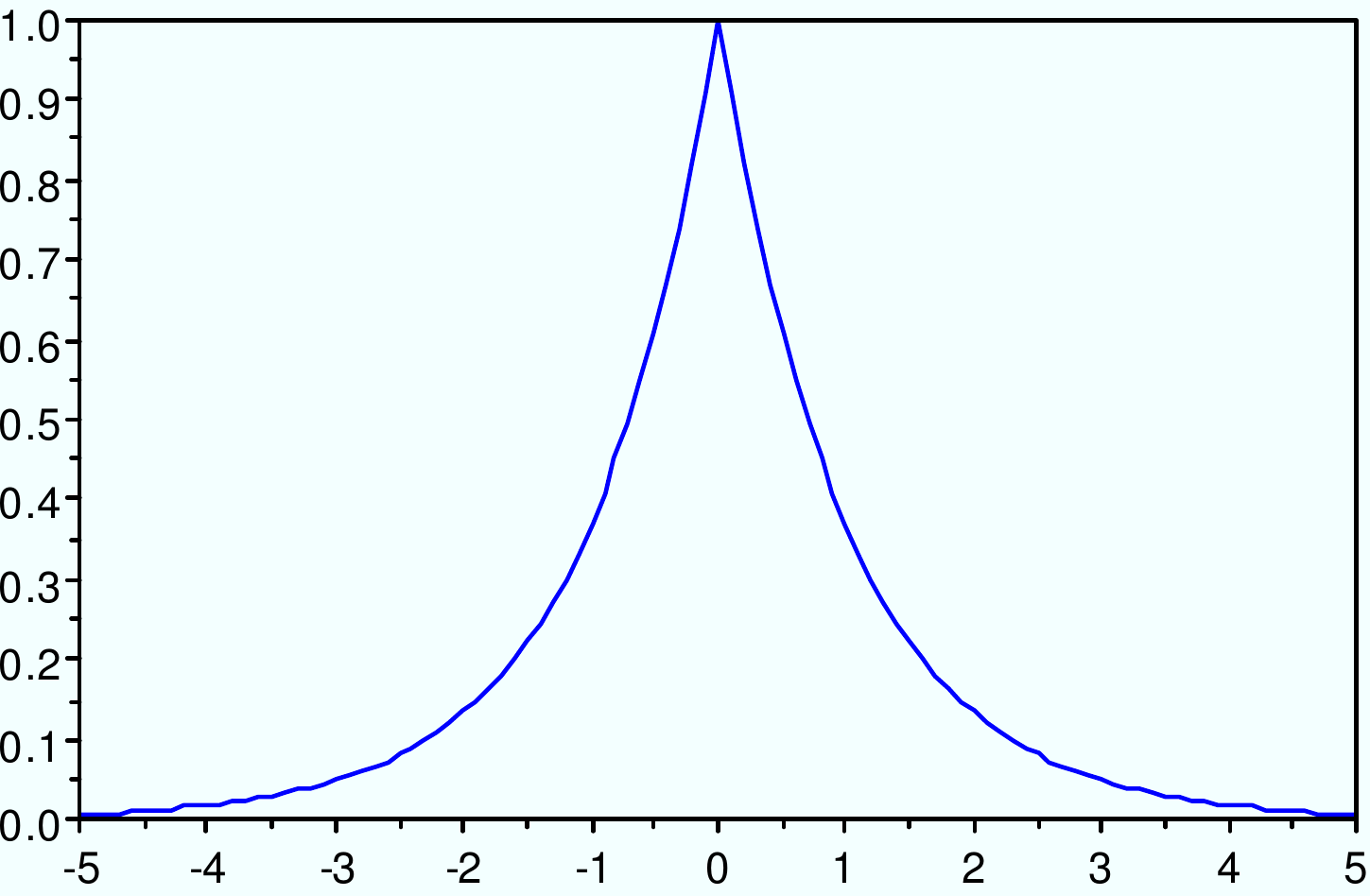
Fig. 56 Noyau exponentiel : \(K(x_i, x_j) = \exp(-\gamma ||x_i-x_j||)\)

• Noyau gaussien : \(K(x_i, x_j) = exp(-\gamma ||x_i-x_j||^2)\)

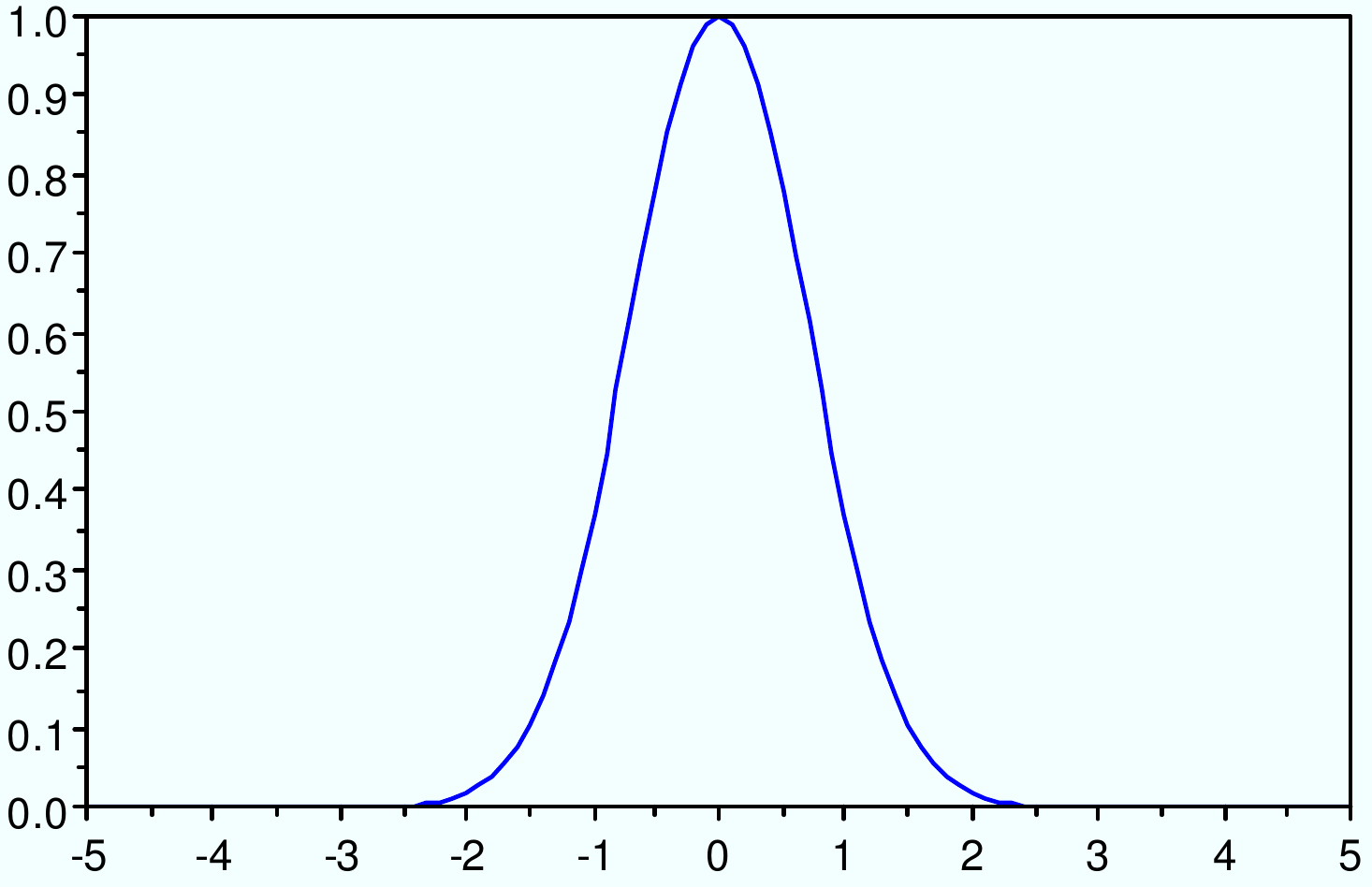
Fig. 57 Noyau gaussien : \(K(x_i, x_j) = exp(-\gamma ||x_i-x_j||^2)\)

• Noyau hyperbolique : \(K(x_i, x_j) = \frac{1}{\epsilon + \gamma||x_i-x_j||}\)

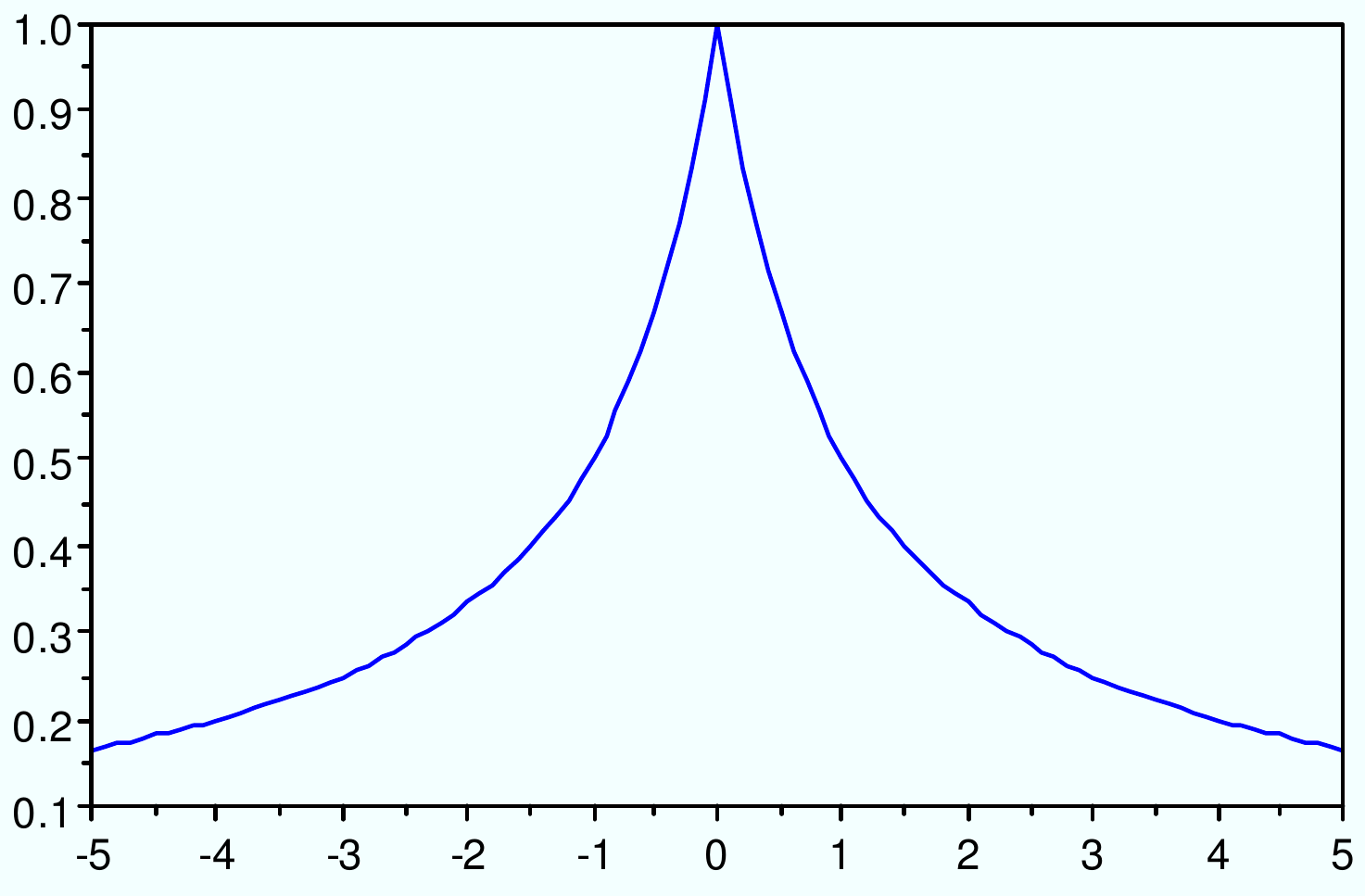
Fig. 58 Noyau hyperbolique : \(K(x_i, x_j) = \frac{1}{\epsilon + \gamma||x_i-x_j||}\)

• Noyau angulaire : \(K(x_i, x_j) = -||x_i-x_j||\)

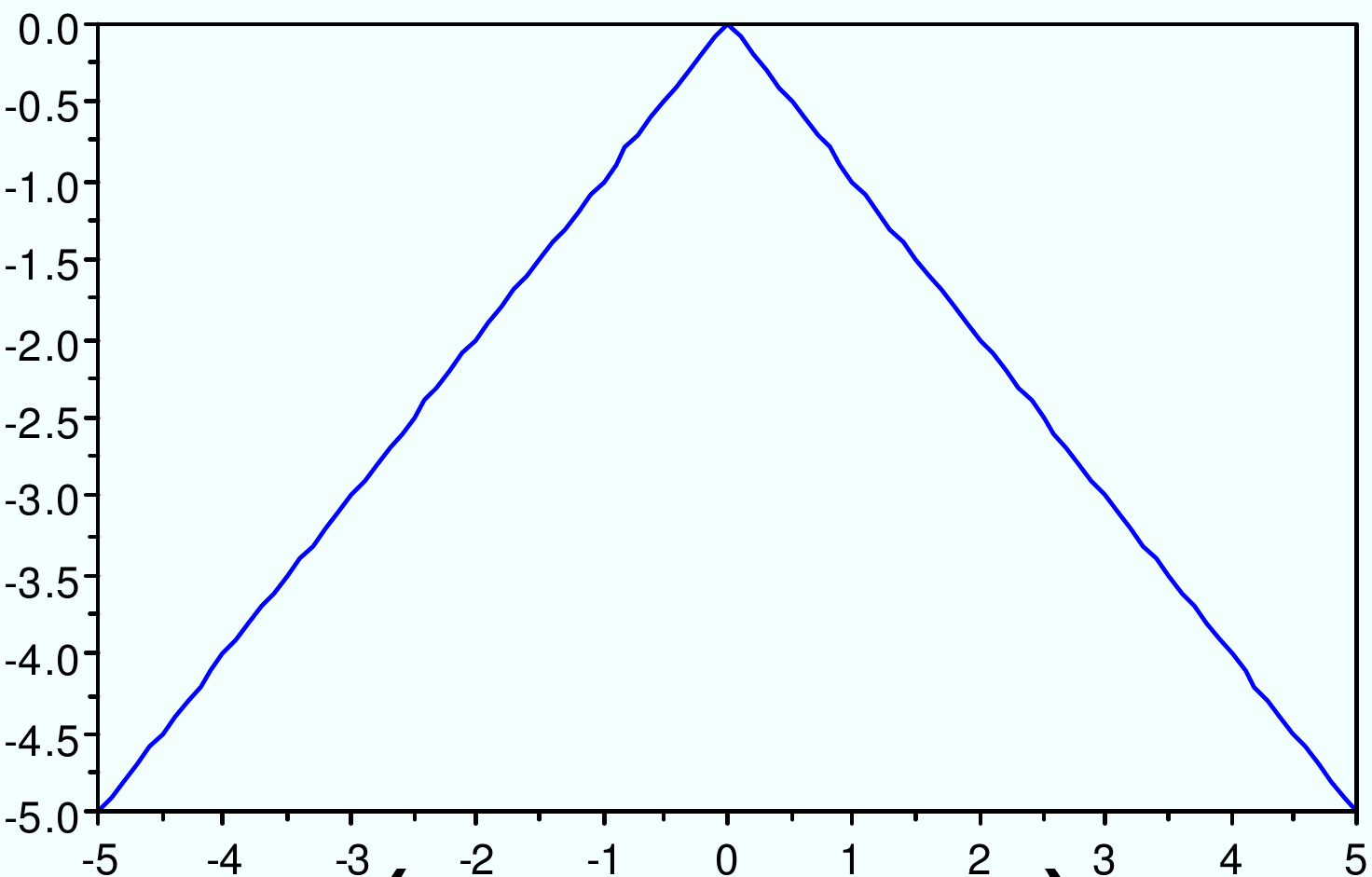
Fig. 59 Noyau angulaire : \(K(x_i, x_j) = -||x_i-x_j||\)

• Noyau puissance : \(K(x_i, x_j) = -||x_i-x_j||^\beta, 0< \beta < 2\)

Même si souvent ce n’est pas possible, parfois on peut écrire analytiquement l’expression de la transformation \(\phi\), ce qui permet d’avoir une vision géométrique directe de la projection des données.

Exemple : noyau polynomial de degré 2, \(K(\mathbf{x_i}, \mathbf{x_j}) = (1 + \mathbf{x_i}^T \mathbf{x_j})^2\).

Dans ce cas \(\mathcal{X} = \mathbb{R}^2, \textrm{ et } \mathbf{x_i} = (x_i, y_i), \mathbf{x_j} = (x_j, y_j)\).

En développant, \(K(\mathbf{x_i}, \mathbf{x_j})\) s’écrit :

\[K(\mathbf{x_i}, \mathbf{x_j}) = \begin{bmatrix} 1 \\ \sqrt{2}x_i\\ \sqrt{2}y_i\\ x_i^2\\ \sqrt{2}x_i y_i\\ y_i^2\\ \end{bmatrix}^T \begin{bmatrix} 1 \\ \sqrt{2}x_j\\ \sqrt{2}y_j\\ x_j^2\\ \sqrt{2}x_j y_j\\ y_j^2\\ \end{bmatrix}\]

On obtient un produit scalaire en dimension 6 (et l’expression analytique de la fonction \(\phi\)).

SVM non-linéaire

On reprend maintenant les machines à vecteurs de support (SVM) pour un problème non-linéaire de classement. Le problème d’optimisation dans le cas des données non-séparable est (voir le cours précédent) :

\[\left\{ \begin{array}{lll} \underset{w,b}{\min} \frac{1}{2}||w||^2 + C \sum_{i=1}^n\xi_i\\ \textrm{t.q.}\\ y_i(w\cdot x_i + b) \geq 1 - \xi_i, i = 1, \dots, n\\ \xi_i \geq 0, i = 1, \dots, n \end{array} \right.\]

La séparation entre les classes étant non linéaire, un séparateur linéaire n’est pas adapté (produira beaucoup d’erreurs de classification). Les données \(x_i\) sont projetées dans l’espace \(\mathcal{H}\) de très grande dimension, \(x_i\rightarrow\phi(x_i)\). Dans \(\mathcal{H}\) les projections \(\phi(x_i)\) ont plus de chances d’être séparables linéairement.

Le problème d’optimisation dans l’espace \(\mathcal{H}\) est:

\[\left\{ \begin{array}{lll} \underset{w,b}{\min} \frac{1}{2}||w||^2 + C \sum_{i=1}^n\xi_i\\ \textrm{t.q.}\\ y_i(\langle w, \phi(x_i)\rangle + b) \geq 1 - \xi_i, i = 1, \dots, n\\ \xi_i \geq 0, i = 1, \dots, n \end{array} \right.\]

SVM non-linéaire : le problème dual est donc

\[\left\{ \begin{array}{llll} \underset{\alpha}{\max} \sum_{i=1}^n \alpha_i - \frac{1}{2}\sum_{i,j=1}^n \alpha_i \alpha_j y_i y_j \langle \phi(x_i), \phi(x_j)\rangle \\ \textrm{t.q.}\\ C \geq \alpha_i \geq 0, i = 1, \dots, n\\ \sum_{i=1}^n \alpha_i y_i = 0 \end{array} \right.\]

Mais par l’astuce des noyaux \(\langle \phi(x_i), \phi(x_j)\rangle = K(x_i, x_j)\) et le problème peut être résolu sans expliciter la projection \(\phi\) (ce qui est souvent très difficile).

\[\left\{ \begin{array}{llll} \underset{\alpha}{\max} \sum_{i=1}^n \alpha_i - \frac{1}{2}\sum_{i,j=1}^n \alpha_i \alpha_j y_i y_j K(x_i, x_j)\\ \textrm{t.q.}\\ C \geq \alpha_i \geq 0, i = 1, \dots, n\\ \sum_{i=1}^n \alpha_i y_i = 0 \end{array} \right.\]

La fonction de décision est donnée par :

\[f(x) = \sum_{i=1}^n \alpha_i y_i K(x_i, x) + b \]

Observations :

• Les \(\alpha\) sont issus du problème dual.

• Pour une meilleure stabilité numérique, \(b\) est obtenu à partir de la moyenne sur l’ensemble \(I\) des vecteurs pour lesquels \(0 < \alpha_i < C\) :

  \[b = \frac{1}{|I|}\sum_{x_j\in I}\left( y_j - \sum_{i=1}^{n} \alpha_i y_i K(x_i, x_j)\right) \]

L’effet des paramètres

Les paramètres sont la constante de régularisation \(C\) et les paramètres du noyau (souvent le paramètre d’échelle \(\gamma\)). Le choix des bonnes valeurs pour ces paramètres et importante et se fait souvent par validation croisée. Un mauvais choix des paramètres conduit à un modèle qui ne généralise pas bien.

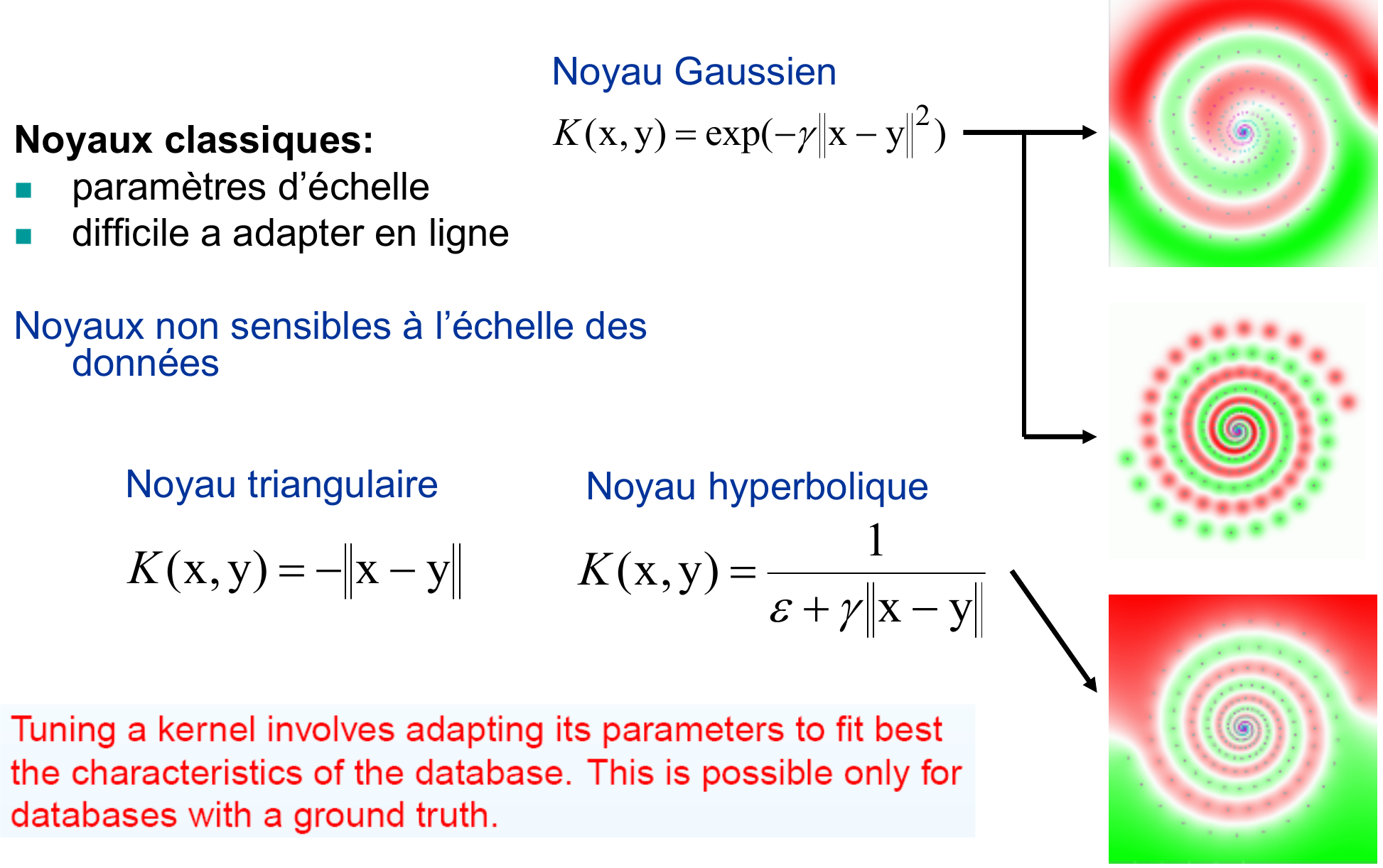
Fig. 60 Paramètre d’échelle : si le paramètre a une valeur trop petite (sigma grand pour un noyau gaussien) on est en situation de sous-apprentissage (image d’en haut), si le paramètre a une valeur trop trop grande (sigma petit) on est en situation de sur-apprentissage (image au milieu). Dans les cas où le séparateur doit fonctionner à plusieurs échelles, comme pour le problème de la spirale dans la figure, il est conseillé d’utiliser un noyau de type angulaire ou hyperbolique, qui a la propriété de bien séparer les données quelle que soit l’échelle (image d’en bas).

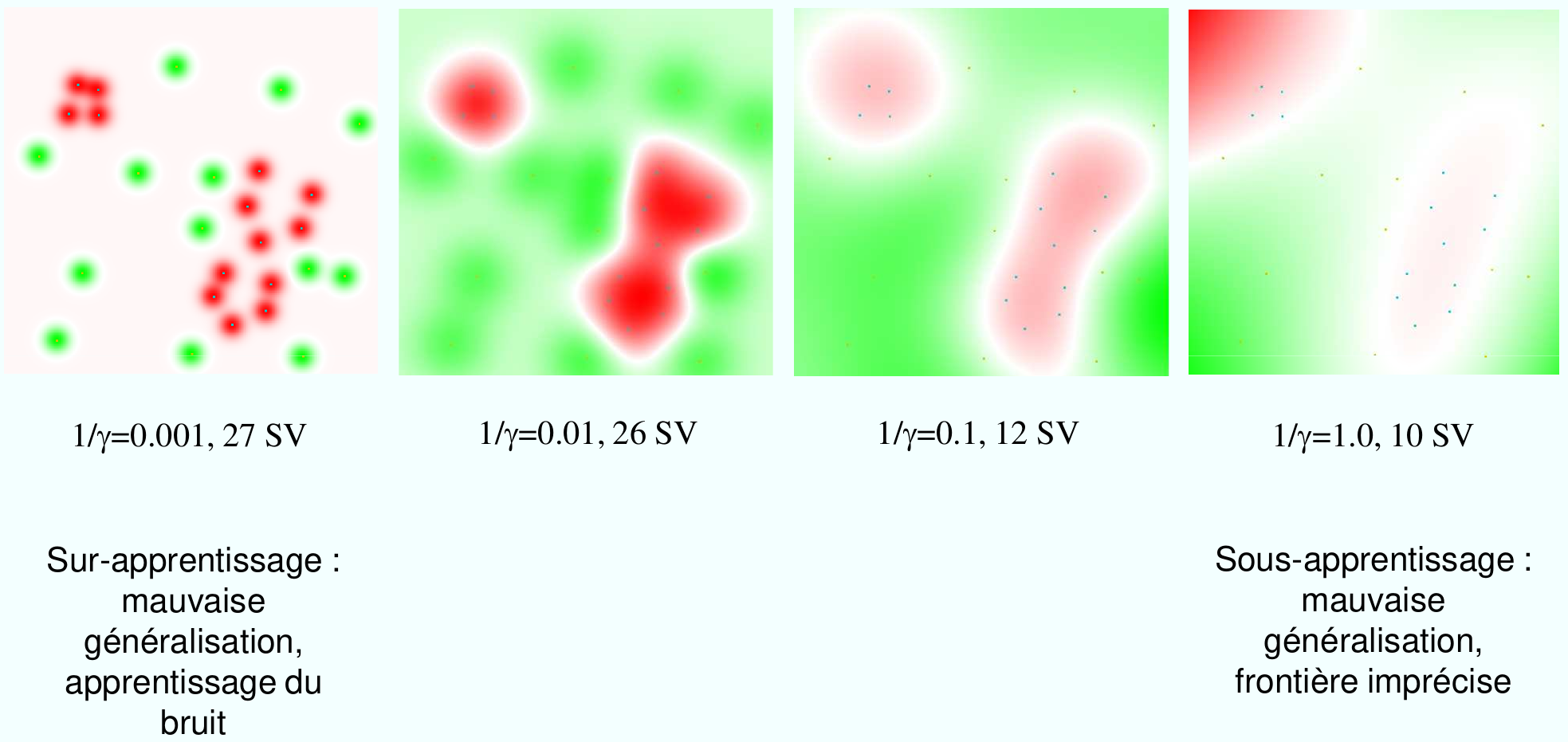
Fig. 61 L’effet du paramètre \(\gamma\) dans un problème d’apprentissage avec un noyau gaussien.

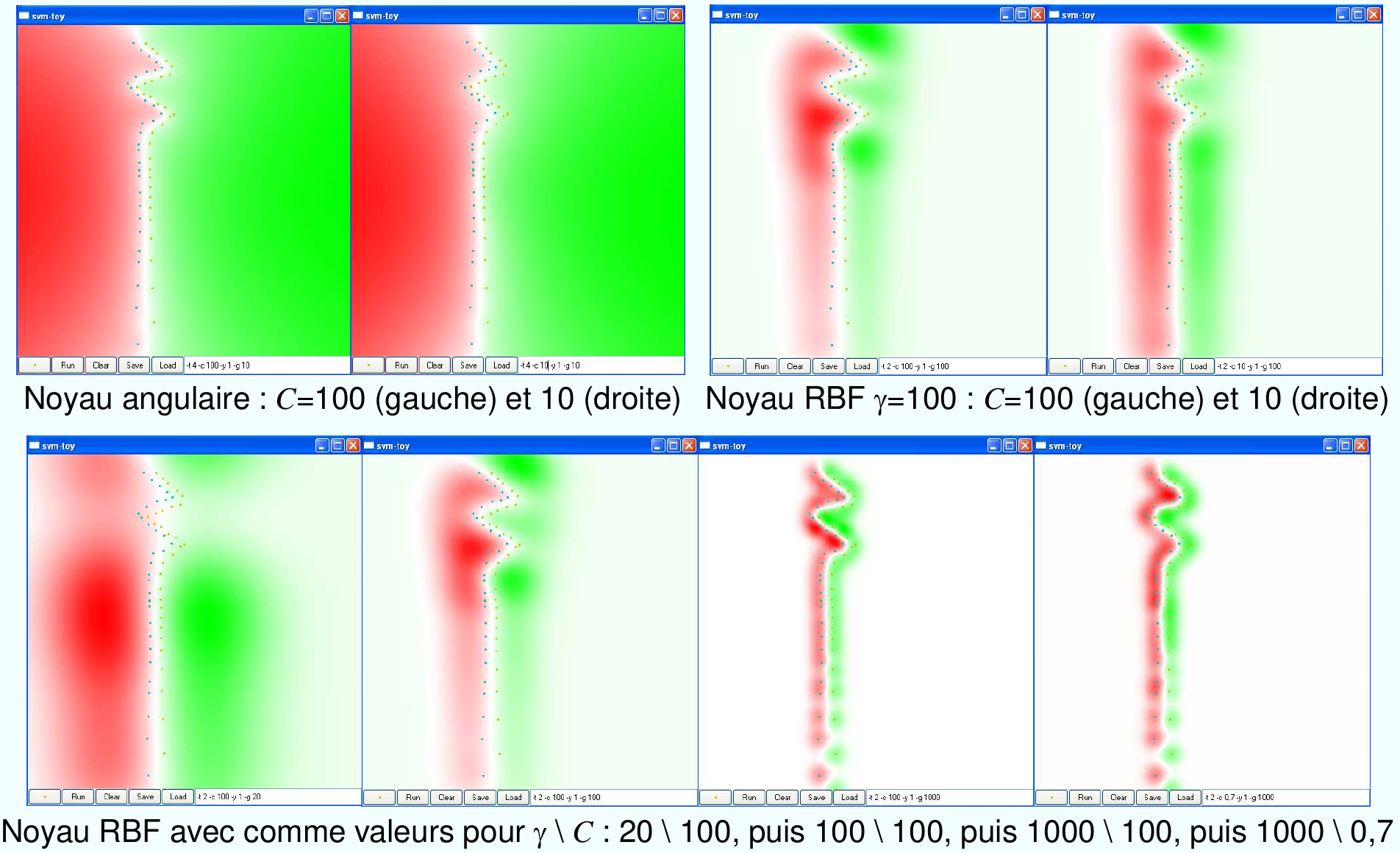
Fig. 62 L’effet des paramètres \(C\) et \(\gamma\) dans un problème d’apprentissage avec un noyau gaussien.

Références : livres, articles, web

[CM12]

Cornuéjols, Miclet, Apprentissage artificiel : concepts et algorithmes, Eyrolles, 2012.

[SC08]

Steinwart, Christmann, Support Vector Machines, Springer, 2008.

[SS01]

Scholkopf, Smola, Learning with Kernels, The MIT Press, 2001.

[HTF06]

Hastie, Tibshirani, Friedman, The elements of statistical learning: data mining, inference, and prediction, New York, Springer Verlag, 2006.

[WikiStat]

Machines à vecteurs supports (WikiStat), http://wikistat.fr

[Bou05] (1,2)

Boughorbel, S., Noyaux pour la classification d’images par les Machines à Vecteurs de Support. Thèse de doctorat, Université d’Orsay, 2005.