Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.
Cours - Réseaux de neurones convolutifs¶
Bien que le théorème d’approximation universel donne des garanties théoriques intéressantes sur les perceptrons multi-couches, ces modèles ont pourtant des limitations pratiques considérables. En effet, l’utilisation de couches entièrement connectées n’est pas adapté à tous les types d’observation.
Considérons par exemple un problème de classification d’images, comme la classification de chiffres manuscrits à partir d’images en noir et blanc comme celles du jeu de données MNIST. Si l’on utilise un perceptron multi-couche avec une seule couche cachée de \(n\) neurones, alors le nombre de paramètres pour la première couche est en \(O(wh\times n)\) avec \(w\) et \(h\) respectivement la largeur et la hauteur des images.
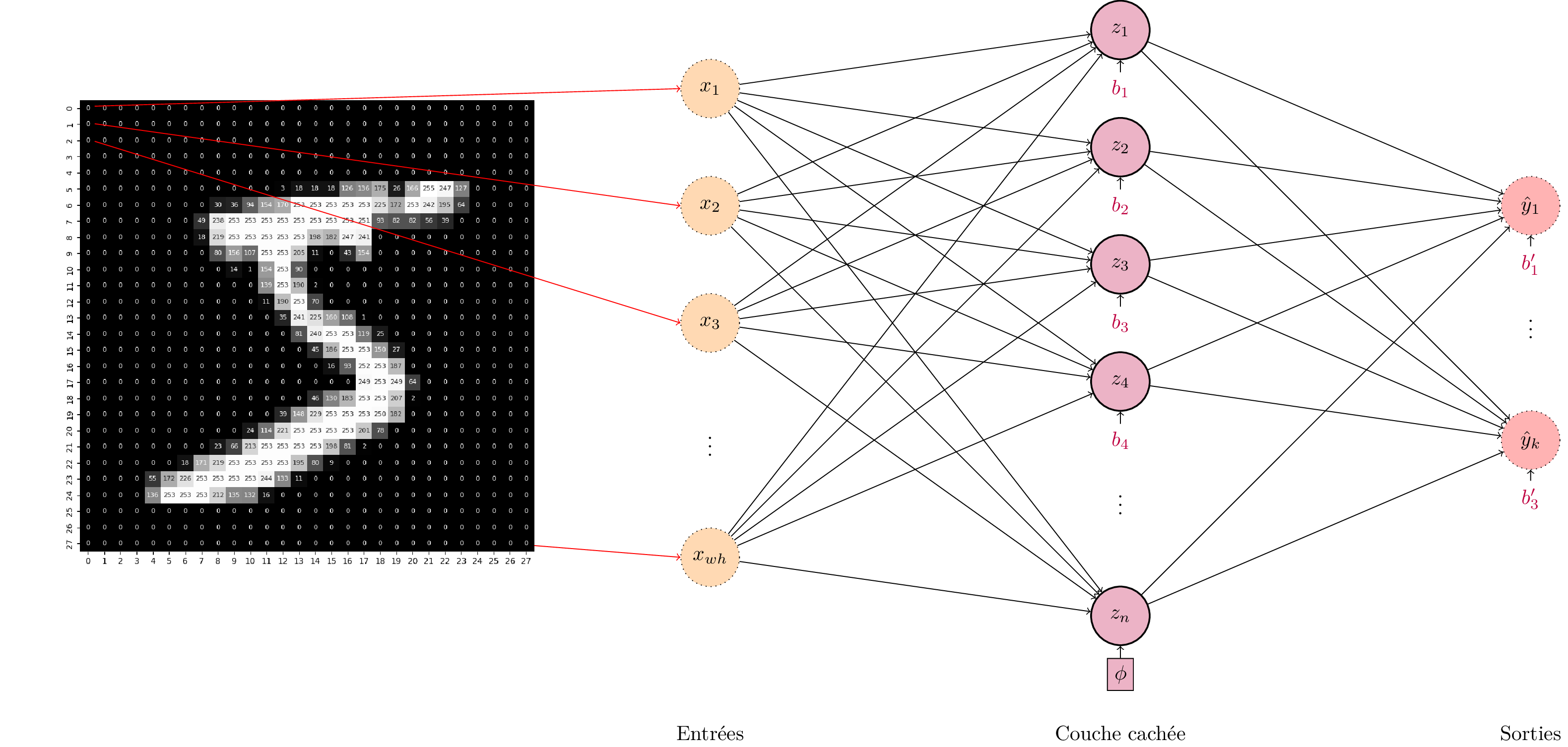
Le nombre de paramètres du perceptron multi-couche croit rapidement avec la dimension de l’entrée et la dimension de la couche cachée. Pour des images au-delà de quelques dizaines de pixels de côté, le nombre de paramètres devient de l’ordre du million.¶
Pour des petites images comme celles de MNIST, cela représente \(28\times 28 = 784\) pixels d’entrée. Pour une couche cachée d’environ 100 neurones, le nombre de paramètres est donc approximativement 80000. Mais la plupart des images de la vie courante sont nettement mieux résolues. Pour une image \(1000\times1000\), nous aurions un million de pixels, soit un milliard de paramètres pour une couche cachée de seulement 1000 neurones!
Cette explosion du nombre de paramètres pose deux problèmes. Premièrement, les coûts calculatoires augmentent, aussi bien le temps de calcul que la mémoire nécessaire au stockage des poids du modèle. Deuxièmement, l’augmentation massive du nombre de paramètres favorise le surapprentrissage et complique donc la modélisation décisionnelle.
Qui plus est, il est assez intuitif de voir qu’il n’est pas probablement pas nécessaire de connecter tous les pixels de l’image d’entrée à tous les pixels de l’image. La sémantique des images peut se déduire en observant les structures locales et en les combinant. Par exemple, en considérant les déformations ci-dessous, on remarque assez rapidement que le catégorie de l’image (la lettre « A ») ne change pas lorsque l’on modifie localement les valeurs des pixels.
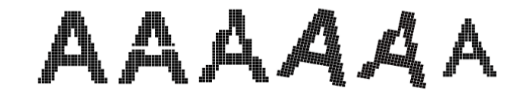
De légères déformations géométriques (translation, rotation, warping) ne changent pas la sémantique de l’image. La classe de l’image est invariante à ces déformations. Cette invariance est difficile à modéliser pour des perceptrons, qui n’ont aucune notion de structure locale.¶
On dit alors que la classe des images est invariantes à certaines transformations. Notamment, la classe d’un objet est invariante à la translation: un chat est un chat, peu importe sa position dans l’image. Pourtant, ces invariances sont difficiles à modéliser pour des perceptrons. En effet, les perceptrons connectent tous les pixels à tous les autres pixels. En représentant une image sous sa forme vectorielle, on ne considère plus sa structure spatiale 2D mais seulement un « sac de pixel » dont on peut réarranger l’ordre comme on le souhaite sans modifier les performances de classification du perceptron.

Apprendre un perceptron multi-couche les images originales de MNIST ou sur les images dont on a permuté l’ordre des pixels ne change pas les performances du modèle. En effet, le perceptron considère les valeurs de chaque indépendamment de toutes les autres. Intuitivement, on comprend ainsi pourquoi les invariances sont difficiles à modéliser par ce type de modèle.¶
Il semble donc y avoir un intérêt à ajouter un a priori dans notre modèle. Puisque la structure locale est importante, il est probablement pertinent de ne connecter un pixel qu’à son voisinage proche. Et comme nos prédictions devraient être invariantes à la translation, il faut donc appliquer les mêmes transformations sur chaque région de l’image.
Ces constats ont amené à l’idée du partage de poids dans les réseaux de neurones. Le Neocognitron de Fukushima (1980) est le premier modèle à avoir appliqué ce principe. Plutôt que d’appliquer un perceptron multi-couche sur toute l’image, on applique un ensemble de perceptrons sur chaque région de l’image. Pour économiser le nombre de paramètres, tous les perceptrons partagent les mêmes poids. C’est l’ancêtre des réseaux de neurones convolutifs.
Convolution¶
La convolution est un opérateur mathématique particulièrement courant en traitement du signal. Le produit de convolution entre deux fonctions \(f: \mathbb{R} \rightarrow \mathbb{R}\) et \(g: \mathbb{R} \rightarrow \mathbb{R}\), habituellement noté \(f * g\), est défini par:
Pour rappel, l’opérateur de convolution a quelques propriétés qui facilitent sa manipulation. Il est notamment :
Commutatif : \(f * g = g * f\).
Associatif : \((f * g) * h = f * (g * h)\).
Bilinéaire : \((\lambda f) * g = \lambda (f * g)\) et \((f + f') * g = f * g + f' * g\)).
Même si la définition ci-dessus vaut pour les fonctions univariées, elle s’étend sans difficulté aux fonctions de plusieurs variables. Dans ce cas, l’intégrale porte alors sur l’ensemble des variables (intégrale multiple).
Lien avec la transformée de Fourier
L’ubiquité des convolutions en traitement du signal s’explique de par leur relation avec la transformée de Fourier, qui est un outil central en analyse harmonique. En effet, la transformée de Fourier \(\mathcal{F}\) transporte les convolutions dans l’espace réel en multiplications dans l’espace spectral, et inversement:
Convolution discrète¶
En pratique, les signaux manipulés sont représentés numériquement sur un support discret, c’est-à-dire que l’on manipule une fonction \(f: \mathbb{Z} \rightarrow \mathbb{R}\). Dans ce cas, le produit de convolution se réécrit:
Dans cette formulation, \(f\) et \(g\) sont des fonctions (des « signaux ») unidimensionnels. Pour des images, qui sont des signaux 2D, on peut sans difficulté étendre cette définition. En deux dimensions, si l’on note \(I : \llbracket 1;w \rrbracket \times \llbracket 1;h \rrbracket \rightarrow \mathbb{R}\) une image \(I\) de taille \(w\times{}h\) et \(Kg \llbracket 1;k_w \rrbracket \times \llbracket 1;k_h \rrbracket \rightarrow \mathbb{R}\) le noyau de convolution de dimension \(k_w \times k_h\), alors on définit le filtre \(\mathcal{K}\) tel que,:
avec \(p = \frac{k_w-1}{2}\) et \(q = \frac{k_h-1}{2}\).
En traitement des images, les filtres convolutifs sont des briques de base pour de nombreuses opérations : débruitage, détection de contours, amélioration de la netteté, etc.

Exemple d’un filtre convolutif calculant les gradients verticaux d’une image à l’aide d’un filtre de Prewitt.¶
Concrètement, la convolution consiste à faire passer une fenêtre glissante de dimensions \(k_w \times k_h\) le long d’une image à filtrer, en se déplaçant d’un pixel à la fois.

Illustration d’une convolution valide. Le noyau de convolution passe en fenêtre glissante pixel à pixel. La valeur du pixel \((i,j)\) est la somme des produits des pixels dans le voisinage \((i,j)\) de l’image initial et du noyau de convolution.¶
Un des inconvénients de ce produit est que le noyau de convolution \(K\) et l’image \(I\) sont parcourus en sens inverse, les indices de l’un augmentant tandis que les indices de l’autre décroissent. En pratique, la plupart des bibliothèques implémentent l’opérateur \(\star\) de corrélation croisée:
Cet opérateur perd la commutativité mais est plus simple à programmer. Dans notre cas, cela ne fera aucune différence car les valeurs de la matrice \(K\) seront des paramètres appris. Il est équivalent d’utiliser une corrélation croisée ou une convolution, les matrices étant identiques à symétrie près. Comme nous le verrons plus tard, les autres opérations intervenant dans les réseaux de neurones convolutifs ne sont de toute façon pas commutatives. La perte de cette propriété est donc sans importance. Dans la suite, on utilisera indifféremment la convolution ou la corrélation croisée.
La corrélation croisée et la convolution souffrent toutes deux d’une inconnue lorsque l’opérateur agit sur les bords, puisque les valeurs de \(I\) hors de l’image sont indéfinies. En règle générale, on ne calcule pas ces valeurs et les lignes et colonnes pour lesquelles le produit de convolution est indéfini sont ignorées, ce qui réduit la taille effective de l’image. On parle alors de corrélation croisée valide. Il est également possible de remplir les valeurs manquantes de \(I\) par des zéros (zero-padding), pour un nombre de lignes et de colonnes égal à la moitié de la taille du noyau de convolution dans chaque direction. On parle alors de corrélation croisée identique, car le résultat du filtrage est de même dimension que l’image d’entrée. Enfin, il est possible de remplir les valeurs manquantes par autant de zéros que nécessaire pour que chaque élément de \(I\) soit visité par chaque élément de \(K\), auquel cas on parle de corrélation croisée complète.

Illustration d’une convolution avec padding. Le noyau de convolution passe en fenêtre glissante pixel à pixel. Aux bords de l’image initial, des colonnes et des lignes de zéro sont ajoutées afin que la convolution puisse être calculée pour toutes les positions \((i,j)\).¶
Couche convolutive¶
En pratique, une couche de convolution en dimension \(n\) d’un réseau de neurones qui s’applique sur un tenseur d’entrée avec \(C_\text{in}\) canaux est paramétrée par:
Les dimensions \((k_1, \dots, k_n)\) des noyaux de convolution, généralement identique selon toutes les dimensions,
Le nombre \(C_\text{out}\) de convolutions parallèles, qui définit le nombre de cartes d’activations en sortie de couche,
Le pas \(s\) de la convolution,
Le padding \(p\).
La couche convolutive comporte un noyau de convolution pour chaque couple (canal d’entrée, canal de sortie). Ainsi, une couche de convolution possède \(k_1 \times \dots \times k_n \times C_\text{in} \times C_\text{out}\) paramètres optimisables. Dans le cas le plus courant de la dimension 2, les noyaux de convolution sont généralement carrés, c’est-à-dire qu’une couche de convolution 2D contient \(C_\text{in} \times C_\text{out} \times k^2\) paramètres.
L’intérêt de la convolution dans les réseaux de neurones profonds est triple [3GBC16]:
Les interactions convolutives sont parcimonieuses, la taille des noyaux de convolution étant très faible devant la taille des images
Les caractéristiques extraites par convolution sont équivariantes aux translations de l’image, c’est-à-dire qu’une translation de l’image d’entrée translate les cartes d’activation de la même façon,
Les paramètres de la convolution sont partagés pour l’ensemble de l’image, ce qui permet de détecter les mêmes caractéristiques peu importe leur position dans l’image avec un très faible coût de stockage en mémoire des paramètres.
Comparée à une couche entièrement connectée, la couche convolutive n’est pas invariante à la permutation des pixels car elle possède un a priori fort sur la structure spatiale des données. Cet a priori est lié à la notion d’équivariance sémantique des images par rapport à certaines transformations géométriques. Néanmoins, il faut garder à l’esprit que cette connaissance structurelle n’est pas toujours respectée. Dans une série temporelle, l’apparition d’une anomalie peut avoir un sens différent en fonction du moment auquel elle se produit. À l’inverse, la convolution 1D part du principe que l’anomalie excitera les neurones de la même façon quelle que soit sa position dans le temps. Cet a priori fort est bien adapté aux images, et tout particulièrement aux images aériennes et satellitaires, qui présentent des régularités spécifiques qui seront détaillées plus tard. La structure même des réseaux de neurones convolutifs est donc adaptée au traitement d’images, qu’ils permettent de décomposer dans un espace de représentation doté d’une équivariance forte à diverses transformations.
Conventionnellement, en 2D, on représente les cartes d’activation des neurones, ou cartes de caractéristiques, sous la forme de tenseurs de dimension 3 \((C, W, H)\) avec \(C\) le nombre de canaux, également appelé nombre de plans de convolutions, \(W\) la largeur et \(H\) la hauteur des cartes.
Une couche convolutive combine les \(n_\text{in}\) cartes d’activation d’entrée avec le \(j\)-ième noyau de convolution \(K_j\)
c’est-à-dire:
Ainsi, une convolution transforme un tenseur \((C_{in}, W_{in}, H_{in})\) en tenseur \((C_{out}, W_{out}, H_{out})\) dont les dimensions spatiales se calculent par :
Note
Les équations d’arithmétique et les illustrations des convolutions sont tirées de [3DV16].
Convolution à pas¶
Une première variante du produit de convolution consiste à sous-échantillonner virtuellement la dimension des cartes d’activation produites d’un facteur \(s\). Pour ce faire, il suffit de ne visiter les éléments de \(I\) qu’avec un pas de \(s\)
Une convolution à pas transforme donc un tenseur \((C_{in}, W_{in}, H_{in})\) en tenseur \((C_{out}, W_{out}, H_{out})\) avec les dimensions spatiales se calculant par
Convolution à trous¶

Illustration d’une convolution dilatée (ou « à trous »). Le noyau de convolution est artificiellement dilaté d’un facteur entier supérieur à 1.¶
La convolution à trous, ou convolution dilatée :footnote:`L'algorithme à trous applique un même filtre à plusieurs échelles en utilisant des convolutions dilatées. La différence entre les deux concepts est subtile mais existe néanmoins.`, consiste à réaliser une convolution en observant \(I\) à une résolution plus faible que sa résolution réelle, en sautant certaines de ses valeurs. Le noyau de convolution est ainsi virtuellement dilaté d’un facteur \(d\), les valeurs manquantes étant remplacées par des 0. En pratique, la convolution à trous se calcule par la formule
Les cartes d’activation en sortie d’une convolution à trous ont pour dimensions
Convolution transposée¶
La convolution transposée est une opération s’opposant à la convolution traditionnelle en ce qu’elle correspond à son gradient par rapport à ses entrées. Pour un noyau de convolution \(k\) donné, la convolution transposée permet de reconstruire une image \(I\) à partir des activations \(Z\), dont les dimensions s’obtiennent par

Illustration d’une convolution transposée (parfois appelée, à tort, déconvolution).¶
Plus prosaïquement, il est possible d’envisager la convolution transposée comme une convolution à pas fractionnel, c’est-à-dire une convolution de pas \(s = \frac{1}{s'}\) avec \(s' \in \mathbb{N}^*\).
Cette convolution est parfois appelée à tort « déconvolution » dans la littérature, sans toutefois correspondre à l’opérateur mathématique éponyme, défini comme l’inverse de l’opérateur de convolution. La convolution transposée est particulièrement utile pour inverser les effets d’une couche convolutive.
Échantillonnage¶
Sous-échantillonnage¶
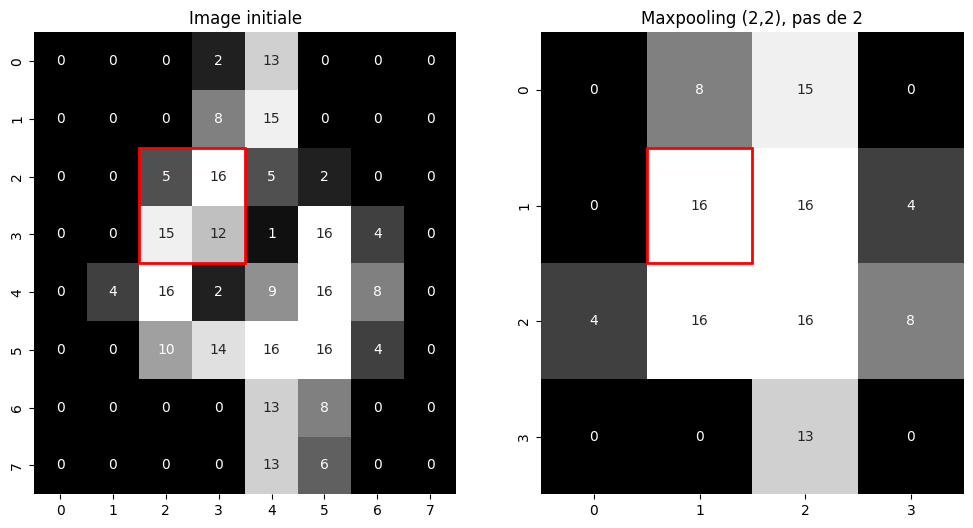
Fig. 103 Sous-échantillonnage d’une image en niveaux de gris par un maxpooling \(2 \times 2\).¶
Afin de réduire la dimension des cartes d’activation dans le réseau, il est utile d’opérer des sous-échantillonnages. Il s’agit généralement d’appliquer un filtre par fenêtre glissante non-recouvrante sur les données d’entrée. Ce filtre est en règle générale l’opérateur \(\max\) ou l’opérateur de moyenne sur une fenêtre de taille fixe. On parle alors de max pooling ou d”average pooling. Un exemple de sous-échantillonnage en 2D est illustré dans la Fig. 103. Dans certains cas, la taille de la fenêtre de sous-échantillonnage n’est pas définie à l’avance mais la dimension des cartes d’activation de sortie l’est. On parle alors de sous-échantillonnage adaptatif. Il est utilisé dans certains réseaux pour réduire brutalement la dimension des cartes d’activation lorsque la taille des images est arbitraire. Dans le cas contraire, les dimensions des couches entièrement connectées déterminent la taille des images d’entrée. Outre la réduction de dimension, l’intérêt de ces opérateurs est d’introduire une invariance aux déformations locales.
Les dimensions d’une carte d’activation en sortie d’un sous-échantillonnage sont
Le sous-échantillonnage n’a pas de paramètre optimisable, il s’agit d’une fonction complètement déterminée.
Sur-échantillonnage¶
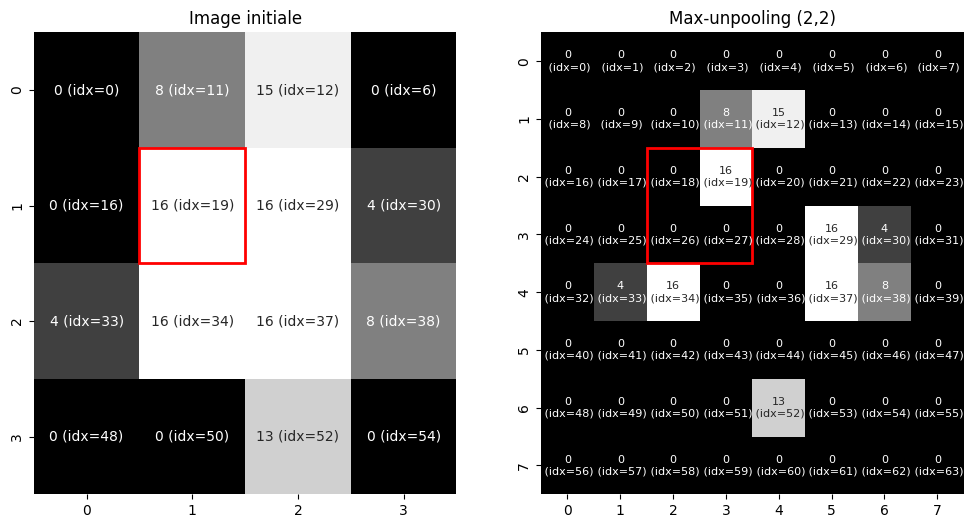
Fig. 104 Sur-échantillonnage (maxunpooling) d’une image en niveaux de gris. Pour réaliser cette opération, il est nécessaire d’avoir conservé en mémoire les indices correspondant aux positions des maxima dans l’image avant le maxpooling.¶
Le sur-échantillonnage, ou unpooling, est l’opération inverse du sous-échantillonnage et tente de reconstruire une entrée à partir de sa sortie. Le sous-échantillonnage étant une opération perdant de l’information, le sur-échantillonnage est approximatif. Dans le cas du sur-échantillonnage par valeur moyenne, la même valeur sera répliquée plusieurs fois dans l’image à résolution augmentée. Dans le cas du sur-échantillonnage par valeur maximale, le maximum sera replacé à sa position initiale et les valeurs restantes complétées par des zéros, comme illustré dans la Fig. 104.
Les dimensions d’une carte d’activation en sortie d’un sur-échantillonnage sont
Comme pour le sous-échantillonnage dont il est la transposée, le sur-échantillonnage ne comprend aucun paramètre optimisable.
Réseaux convolutifs¶
L’architecture des réseaux convolutifs de manipuler non plus des matrices, mais des tenseurs. Les tenseurs généralisent les matrices mais ont plus que deux dimensions. Par exemple, une image en couleur est un tenseur de dimensions \((W, H, C)\) avec \(H\) la hauteur en pixels, \(W\) la largeur et C le nombre de canaux (par exemple, 3 pour une image RGB). Une couche convolutive s’applique donc sur ce tenseur et produit en sortie un nouveau tenseur d’activations \((W', H', C')\), dont les dimensions dépendent des hyperparamètres de la couche (nombre de canaux de sortie, dimensions des noyaux de convolution, padding, stride).
La plupart des réseaux de neurones convolutifs (ou Convolutional Neural Networks, CNN) fonctionnent en deux blocs. Le premier bloc contient en alternance une couche convolutive, une activation non-linéaire et un sous-échantillonnage spatial (maxpooling). Cette combinaison est répétée plusieurs fois. Le sous-échantillonnage permet de réduire les dimensions spatiales du tenseur d’activation. En compensation, on augmente généralement le nombre de filtres convolutifs dans les couches ultérieures. Lorsque ces dimensions sont suffisamment réduites, on peut « aplatir » le tenseur pour obtenir un vecteur. Par exemple, le tenseur \((W, H, C)\) sera aplati en un vecteur de longueur \(W \times H \times C\). Le deuxième bloc est alors un perceptron multi-couche classique, qui va appliquer plusieurs couches entièrement connectées pour transformer le vecteur ainsi obtenu en un vecteur de prédiction. Cette prédiction pourra alors être passée dans une fonction d’activation (par exemple, softmax) puis l’on pourra calculer la valeur de la fonction de coût.
LeNet¶
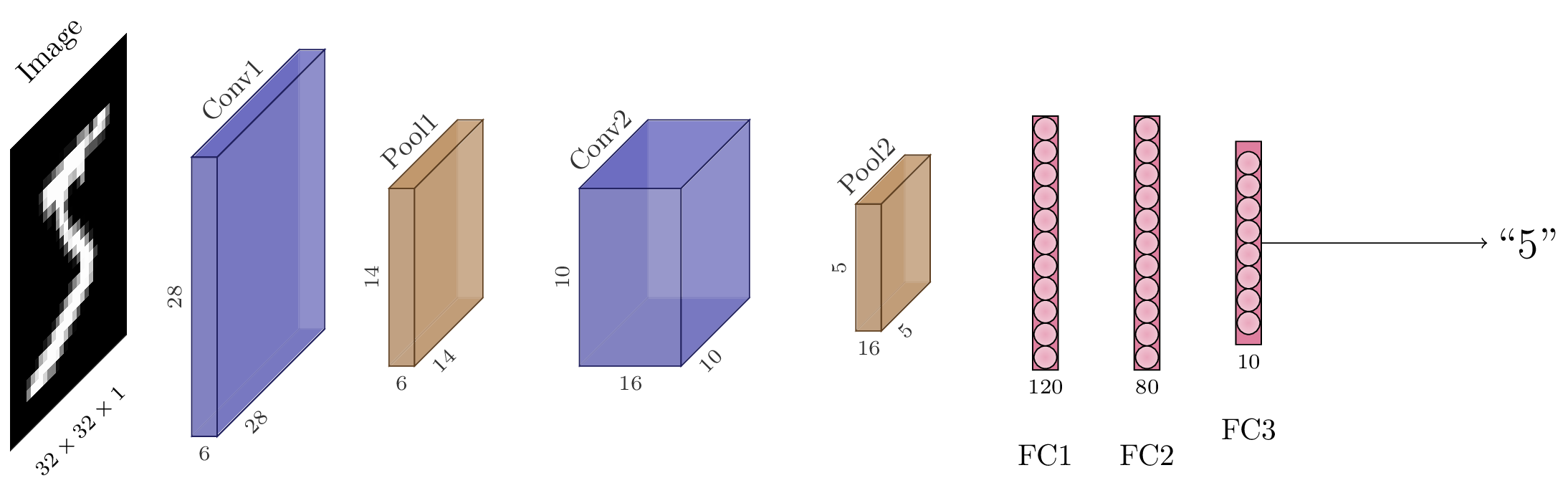
Fig. 105 Schéma de l’architecture LeNet. En couleur sont représentés les différentes cartes d’activation, c’est-à-dire les tenseurs intermédiaires après chaque couche du modèle.¶
Prenons un exemple avec l’architecture LeNet-5 de la Fig. 105. Ce modèle, introduit en 1989 [3LBBH98], utilise cinq « couches » de neurones, c’est-à-dire cinq ensembles de paramètres. Il prend en entrée une image en niveaux de gris (un seul canal) de dimensions \(28\times28\). L’objectif est de reconnaître dans l’image le chiffre manuscrit qui y est inscrit.
La première couche est une couche convolutive de noyaux \(5\times5\), un padding de 2, avec 6 canaux en sortie et une activation sigmoide. L’activation obtenue est donc un tenseur \((28, 28, 6)\).
Elle est suivie d’un maxpooling de fenêtre \(2\times 2\), résultant en un tenseur \((14, 14, 6)\).
La seconde couche est une nouvelle couche convolutive de noyaux \(5\times 5\), sans padding, avec 16 canaux en sortie et une activation sigmoide. L’activation obtenue est un tenseur \((10, 10, 16)\).
Elle est suivie d’un maxpooling de fenêtre \(2\times 2\), résultant en un tenseur \((5, 5, 6)\).
Ce tenseur est aplati (flattened) en un vecteur de longueur 150.
La troisième couche est une couche entièrement connectée, prenant les 150 activations et les projetant en un vecteur de longueur 120. Elle est suivie d’une sigmoide.
La quatrième couche est encore entièrement connectée et projette les 120 activations en 84 activations. Elle est également suivie d’une sigmoide.
La cinquième, et dernière, couche est entièrement connectée et projette les 84 activations en un vecteur de longueur 10 (une composante pour chaque chiffre). Elle est suivie d’une activation softmax.
Le modèle est entraîné par rétropropagation et descente de gradient sur une fonction de coût entropie croisée.
AlexNet¶
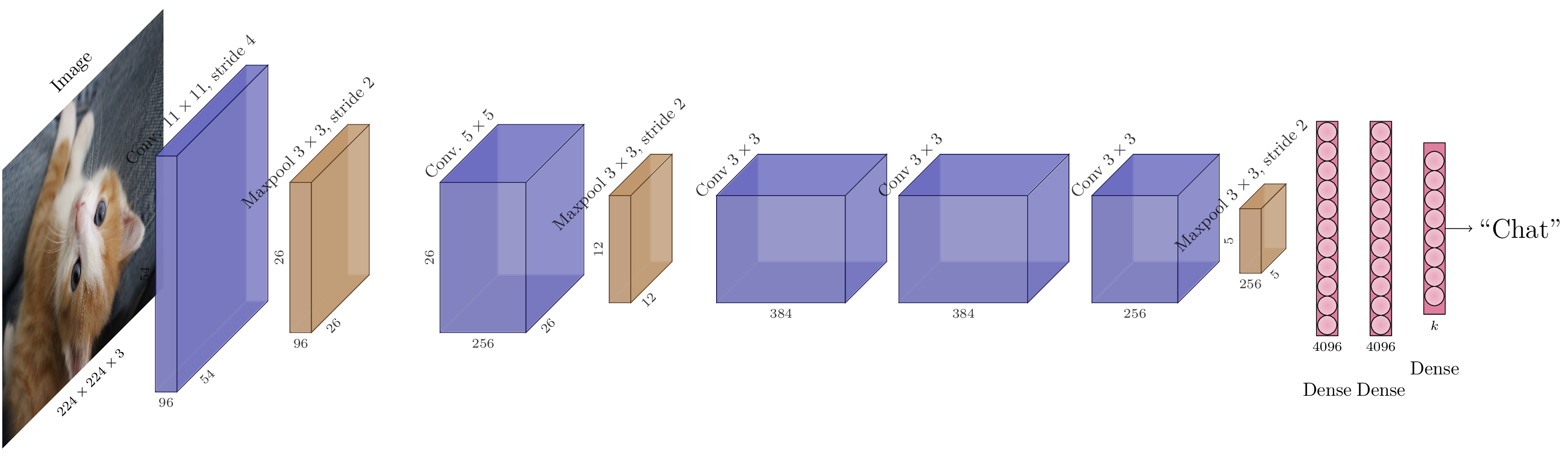
Architecture AlexNet.¶
À partir de 2012, les premiers réseaux de neurones convolutifs s’imposent pour les tâches de reconnaissance d’objet dans des images. en particulier gagne plusieurs compétitions en 2011 et 2012 : identification d’idéogrammes chinois, de lettres et de chiffres manuscrits, reconnaissance de panneaux de signalisation, etc. Ces succès sont principalement dus à l’implémentation parallèle sur GPU de la rétropropagation, accélérant considérablement les temps de calcul (par un facteur 10), et la disponibilité de nouveaux jeux de données de plusieurs dizaines, voire centaine, de milliers d’images.
L’architecture AlexNet [3KSH12] est un réseau convolutif dont la structure n’est pas particulièrement notable. Cependant, il s’agit d’un réseau particulièrement connu puisqu’il a remporté la compétition ILSVRC 2012, consistant à reconnaître automatiquement l’objet représenté dans une image parmi 1000 catégories différentes. AlexNet est le premier modèle de réseau de neurones profond à remporter cette compétition, avec une marge significative (la bonne réponse était parmi le top-5 des réponses d’AlexNet dans 84,7% des images de test, contre 73,9% des cas pour l’algorithme arrivé second). Cette victoire a marqué un tournant dans la vision par ordinateur, puisqu’elle a démontré la possibilité d’entraîner des réseaux profonds sur de vastes quantités de données (un million d’images pour le jeu de données ImageNet, utilisé dans la compétition) en un temps raisonnable à l’aide d’accélérateurs graphiques (GPU). Dans les années qui ont suivi, les recherches en apprentissage profond ont connu une croissance rapide.
L’architecture d’AlexNet est assez simple et comparable à celle de LeNet-5, excepté que le nombre de paramètres est bien plus important :
Couche convolutive de \(96\) canaux, de noyaux \(11\times11\) avec un pas de 4 + activation ReLU,
Maxpooling \(3\times3\) avec un pas de 2,
Couche convolutive de \(256\) canaux, de noyaux \(5\times5\) avec un padding de 2 + activation ReLU,
Maxpooling \(3\times3\) avec un pas de 2,
Couche convolutive de \(384\) canaux, de noyaux \(3\times3\) avec un padding de 1 + activation ReLU,
Couche convolutive de \(384\) canaux, de noyaux \(3\times3\) avec un padding de 1 + activation ReLU,
Couche convolutive de \(256\) canaux, de noyaux \(3\times3\) avec un padding de 1 + activation ReLU,
Maxpooling \(3\times3\) avec un pas de 2,
Couche dense (entièrement connectée) 4096 + activation ReLU,
Dropout (\(p=0.5\))
Couche dense (entièrement connectée) 4096 + activation ReLU,
Dropout (\(p=0.5\))
Couche dense (entièrement connectée) 1000.
L’essentiel des poids se situent dans la partie entièrement connectée du modèle. En effet, en sortie des couches convolutives, le tenseur d’activations a pour dimensions \((5, 5, 256)\), soit une longueur de 6400 une fois aplati en vecteur. La couche suivante étant entièrement connectée et de sortie de dimension 4096, elle contient donc une matrice de poids de \(4096\times6400=26214400\) soit plus de 26 millions de paramètres. Le Dropout est donc une régularisation bienvenue sur la partie perceptron multi-couche du modèle.
VGG¶
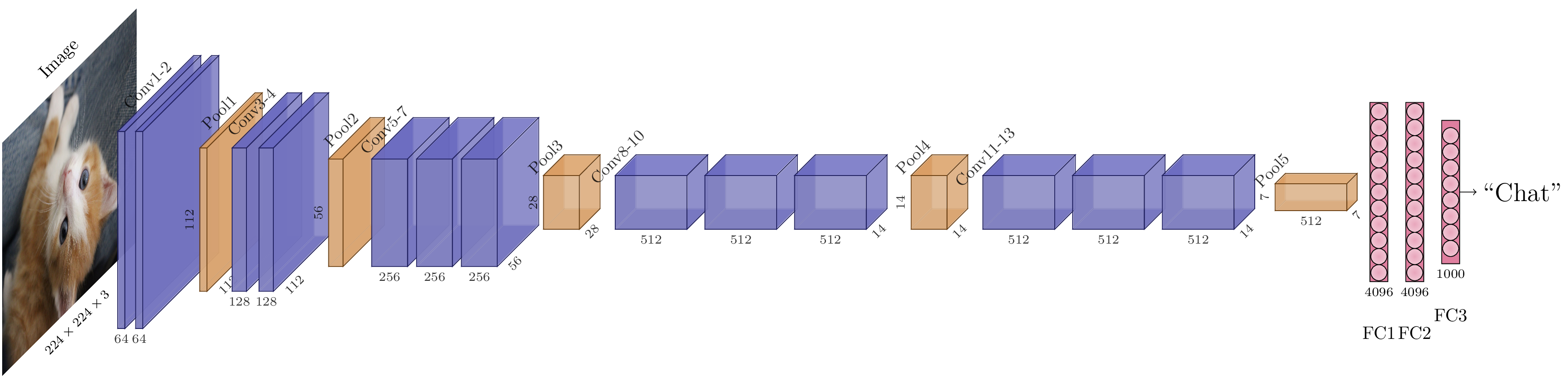
Architecture VGG-16.¶
Les architectures dites « VGG » (pour Visual Geometry Group, une unité de recherche de l’université d’Oxford) [3SZ15], ont été construites afin de proposer un formalisme « standard » pour la construction des CNN. En effet, les réseaux convolutifs ont de nombreux hyperparamètres : nombre de couches, taille des convolutions, choix du padding, etc. Les architectures VGG se fondent sur une observation : les grands noyaux de convolution peuvent être reproduits en appliquant successivement plusieurs petits noyaux de convolution. Cependant, cette deuxième solution est moins coûteuse du point de vue des calculs que la première. Il est donc avantageux dans les CNN d’éviter des filtres trop grands, et de préférer des filtres petits, par exemple \(3 \times 3\). Par ailleurs, il est peu commode qu’une convolution change les dimensions spatiales du tenseur d’activations, car cela complique les raisonnements sur les tailles des tenseurs manipulés. Il faut donc préférer un padding « à l’identique », qui conserve les dimensions spatiales des tenseurs. Pour une convolution \(3\times 3\), cela revient à ajouter un pixel de padding de chaque côté, donc padding de 1. Comme nous utilisons déjà des maxpooling pour réduire les dimensions spatiales, il est par ailleurs redondant d’utiliser un pas de convolution autre que 1.
En résumé, le bloc de base de l’architecture VGG est donc le suivant :
Une couche convolutive à \(C\) canaux, de noyaux \(3 \times 3\), padding 1 et stride 1 suivie d’une activation non-linéaire, par exemple ReLU.
Une seconde couche convolutive à \(C\) canaux, de noyaux \(3 \times 3\), padding 1 et stride 1 suivie d’une activation non-linéaire, par exemple ReLU.
Éventuellement, une troisième couche convolutive à \(C\) canaux, de noyaux \(3 \times 3\), padding 1 et stride 1 et son activation ReLU.
Un maxpooling \(2 \times 2\).
Ce bloc de base est répété autant de fois que nécessaire pour obtenir la réduction spatiale souhaitée (d’un facteur 2, 4, 8, 16, 32, 64, etc.). Une fois la partie convolutive terminée, on applique un perceptron multi-couche à deux couches cachées projetant le vecteur d’activations aplati à la dimension souhaitée pour la sortie du modèle.
Suivre ces préconisations simplifie grandement la construction de CNN, puisque les seuls hyperparamètres à déterminer sont désormais :
la « largeur » des blocs, c’est-à-dire le nombre de canaux \(C\) des couches convolutives,
la profondeur du réseau, c’est-à-dire le nombre de blocs convolutifs.
Cela permet par exemple de définir l’architecture VGG-16, qui utilise deux blocs de 2 convolutions, puis trois blocs de 3 convolutions et enfin un trois couches entièrement connectées.
Vincent Dumoulin and Francesco Visin. A guide to convolution arithmetic for deep learning. arXiv:1603.07285 [cs, stat], March 2016. arXiv:1603.07285.
Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep Learning. MIT Press, 2016.
Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Neural Information Processing Systems (NIPS), 1097–1105. 2012.
Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, November 1998. doi:10.1109/5.726791.
Karen Simonyan and Andrew Zisserman. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations (ICLR). May 2015.
