Travaux pratiques - Réseaux de neurones multicouches (3)¶
(correspond à 1 séance de TP)
Références externes utiles :
L’objectif de cette séance de TP est de comparer les représentations internes développées dans des perceptrons multicouches à des représentations obtenues par réduction de dimension linéaire. Vous pouvez également comparer ces représentations aux résultats des méthodes de réduction de dimension non linéaire examinées dans le TP sur t-SNE et dans celui sur UMAP.
Auto-encodeurs et analyse en composantes principales¶
Données digits¶
Nous nous servons des données digits, un ensemble d’images en faible résolution (8 x 8 pixels) de chiffres manuscrits, déjà disponible dans Scikit-learn. Nous pouvons le charger et en afficher un échantillon avec :
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
X, y = load_digits(return_X_y=True)
print(X.shape)
plt.figure(dpi=100)
for i in range(150):
plt.subplot(10,15,i+1)
plt.imshow(X[i,:].reshape([8,8]), cmap='gray')
plt.axis('off')
plt.show()
Avant de faire apprendre des réseaux de neurones nous séparons les données en ensembles d’apprentissage et de test :
np.random.seed(10)
from sklearn.model_selection import train_test_split
X_train1, X_test1, y_train1, y_test1 = train_test_split(X, y, test_size=0.2)
Analyse en composantes principales et approximation des données¶
Les variables explicatives sont les nuances de gris des 64 pixels des images ; ces variables sont directement comparables, nous n’appliquons donc pas d’opération de réduction (pour faire en sorte que toutes les variances soient égales à 1). Par ailleurs, les pixels périphériques ont naturellement une variance de départ 0 (ou proche de 0) et une opération de réduction serait nocive.
Pour pouvoir mieux comparer ultérieurement la projection sur les deux premières composantes principales aux représentations obtenues par les PMC, nous cherchons également les axes principaux à partir du seul ensemble d’apprentissage.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(X_train1)
print(pca.explained_variance_ratio_[0:20])
X_train1p = pca.transform(X_train1)
X_test1p = pca.transform(X_test1)
plt.figure()
plt.scatter(X_train1p[:,0], X_train1p[:,1], c=y_train1, cmap='coolwarm', s=5)
plt.scatter(X_test1p[:,0], X_test1p[:,1], c=y_test1, cmap='coolwarm', s=5)
plt.colorbar()
plt.title("Projection après ACP")
plt.show()
Le résultat de la projection devrait ressembler à la figure suivante :
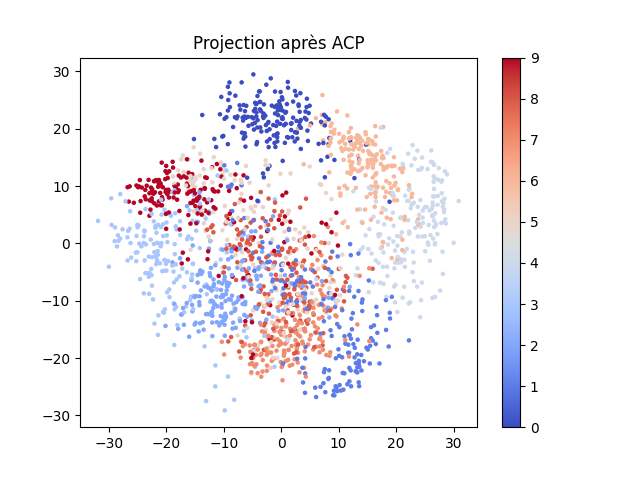
A partir des projections sur les deux premiers axes principaux il est possible de reconstruire (des approximations) des données dans leur espace d’origine. L’approximation d’une donnée est obtenue comme la somme vectorielle des projections sur les vecteurs propres correspondant aux deux plus grandes valeurs propres : np.dot(X_train1p[:,0:2],pca.components_[0:2,:]). Comme les observations de départ avaient été centrées implicitement lors de la réalisation de l’ACP (la moyenne sur chaque variable avait été soustraite de la composante correspondante de chaque observation), il est nécessaire ensuite d’ajouter cette moyenne que nous pouvons obtenir par np.average(X_train1, axis=0). En conséquence :
Xrec2cp_train1 = np.dot(X_train1p[:,0:2],pca.components_[0:2,:]) + np.average(X_train1, axis=0)
print(Xrec2cp_train1.shape)
plt.figure(figsize=(10,2), dpi=100)
for i in range(10):
plt.subplot(2,10,i+1)
# en haut les images d'origine
plt.imshow(X_train1[i,:].reshape([8,8]), cmap='gray')
plt.axis('off')
plt.subplot(2,10,i+11)
# en bas les images reconstituées
plt.imshow(Xrec2cp_train1[i,:].reshape([8,8]), cmap='gray')
plt.axis('off')
plt.show()
Pour comparer, nous avons affiché sur la ligne du haut 10 images d’origine et sur la ligne du bas les images correspondantes obtenues par reconstruction. Le résultat devrait ressembler à celui de la figure suivante :
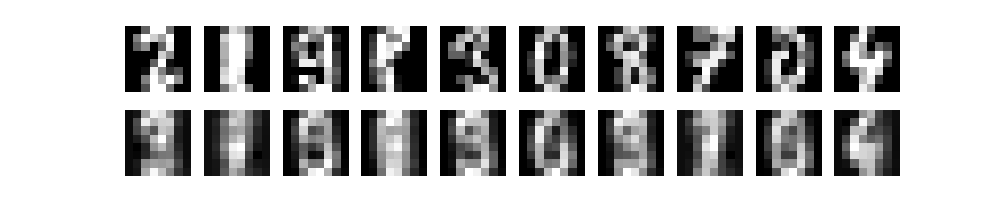
Auto-encodeur linéaire et reconstruction des données¶
Pour illustrer le cas d’un auto-encodeur linéaire, considérons un perceptron à une couche cachée linéaire (activation='identity'), composée de 2 neurones, qui doit apprendre à approximer ses entrées. La fonction de coût pour ce problème de régression est l’erreur quadratique et la classe à employer est MLPRegressor :
from sklearn.neural_network import MLPRegressor
rgs = MLPRegressor(hidden_layer_sizes=(2,), activation='identity', solver='adam', max_iter=5000, random_state=1)
rgs.fit(X_train1, X_train1)
print("Matrice de poids entrées -> couche cachée : {}".format(rgs.coefs_[0].shape))
print("Matrice de poids couche cachée -> sorties : {}".format(rgs.coefs_[1].shape))
# pour la régression le score est le coefficient de détermination
train_score = rgs.score(X_train1, X_train1)
print("Le score en train est {}".format(train_score))
test_score = rgs.score(X_test1, X_test1)
print("Le score en test est {}".format(test_score))
Afin de visualiser les représentations obtenues dans la couche cachée (et les comparer à celles issues de l’ACP) il est nécessaire de les reconstruire car Scikit-learn ne propose aucune méthode d’accès aux activations des neurones cachés. Nous devons donc refaire le calcul réalisé par la première couche du réseau :
activationsLineaires_train1 = np.dot(X_train1,rgs.coefs_[0]) + rgs.intercepts_[0]
activationsLineaires_test1 = np.dot(X_test1,rgs.coefs_[0]) + rgs.intercepts_[0]
L’affichage du résultat peut être fait avec :
plt.figure()
plt.scatter(activationsLineaires_train1[:,0], activationsLineaires_train1[:,1], c=y_train1, cmap='coolwarm', s=5)
plt.scatter(activationsLineaires_test1[:,0], activationsLineaires_test1[:,1], c=y_test1, cmap='coolwarm', s=5)
plt.colorbar()
plt.title("Représentation dans auto-encodeur linéaire")
plt.show()
Question :
Pourquoi les représentations internes issues de l’auto-encodeur linéaire ne sont pas les mêmes que celles obtenus par la projections sur les deux premiers axes principaux ?
Question :
Affichez les reconstructions de quelques exemples d’apprentissage. Vous pouvez utiliser la méthode predict de MLPRegressor.
Auto-encodeur non linéaire et reconstruction des données¶
Nous pouvons maintenant considérer le cas d’un auto-encodeur non linéaire, composé d’une partie encodeur à une couche cachée non linéaire suivie d’une partie décodeur à une couche cachée non linéaire également. Nous conservons une couche de deux neurones seulement à la sortie de l’encodeur. Le perceptron multi-couche employé a donc trois couches cachées, dont la deuxième a seulement deux neurones :
from sklearn.neural_network import MLPRegressor
rgs = MLPRegressor(hidden_layer_sizes=(20,2,20,), activation='logistic', alpha=0.01, solver='adam', max_iter=10000, random_state=10)
rgs.fit(X_train1, X_train1)
print("Matrice de poids entrées -> couche cachée : {}".format(rgs.coefs_[0].shape))
print("Matrice de poids couche cachée -> sorties : {}".format(rgs.coefs_[1].shape))
# pour la régression le score est le coefficient de détermination
train_score = rgs.score(X_train1, X_train1)
print("Le score en train est {}".format(train_score))
test_score = rgs.score(X_test1, X_test1)
print("Le score en test est {}".format(test_score))
Afin de visualiser les représentations obtenues dans la deuxième couche cachée (la sortie de la partie encodeur) il est nécessaire de refaire le calcul réalisé par les deux premières couches du réseau. Nous affichons d’abord les représentations obtenues dans la deuxième couche cachée avant application de la fonction d’activation non linéaire :
activationsNonLineairesCouche1_train1 = 1 / (1 + np.exp(-(np.dot(X_train1,rgs.coefs_[0]) + rgs.intercepts_[0])))
activationsNonLineairesCouche1_test1 = 1 / (1 + np.exp(-(np.dot(X_test1,rgs.coefs_[0]) + rgs.intercepts_[0])))
activationsNonLineaires_train1 = np.dot(activationsNonLineairesCouche1_train1,rgs.coefs_[1]) + rgs.intercepts_[1]
activationsNonLineaires_test1 = np.dot(activationsNonLineairesCouche1_test1,rgs.coefs_[1]) + rgs.intercepts_[1]
plt.figure()
plt.scatter(activationsNonLineaires_train1[:,0], activationsNonLineaires_train1[:,1], c=y_train1, cmap='coolwarm', s=5)
plt.scatter(activationsNonLineaires_test1[:,0], activationsNonLineaires_test1[:,1], c=y_test1, cmap='coolwarm', s=5)
plt.colorbar()
plt.title("Représentation dans auto-encodeur non linéaire")
plt.show()
Question :
Comparez avec le résultat obtenu après application de la fonction d’activation aux deux neurones de la deuxième couche cachée.
Question :
Comparez les reconstructions obtenues avec le dernier auto-encodeur non linéaire à celles obtenues par l’ACP ou par l’auto-encodeur linéaire.
Classification multi-classe et analyse factorielle discriminante¶
Nous nous servons des mêmes données digits pour comparer la projection des données sur les deux premiers axes discriminants aux représentations développées par apprentissage dans un PMC qui doit faire une classification multi-classes.
Analyse factorielle discriminante des données digits¶
Nous avons déjà examiné l’AFD (sur d’autres données) dans une séance de TP dédiée.
np.random.seed(10)
from sklearn.model_selection import train_test_split
X_train1, X_test1, y_train1, y_test1 = train_test_split(X, y, test_size=0.2)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis()
lda.fit(X_train1,y_train1)
X_train1t = lda.transform(X_train1)
X_test1t = lda.transform(X_test1)
plt.figure()
plt.scatter(X_train1t[:,0], X_train1t[:,1], c=y_train1, cmap='coolwarm', s=5)
plt.scatter(X_test1t[:,0], X_test1t[:,1], c=y_test1, cmap='coolwarm', s=5)
plt.colorbar()
plt.title("Projection après AFD")
plt.show()
La projection des données sur les deux premiers axes discriminants devrait ressembler à la figure suivante :
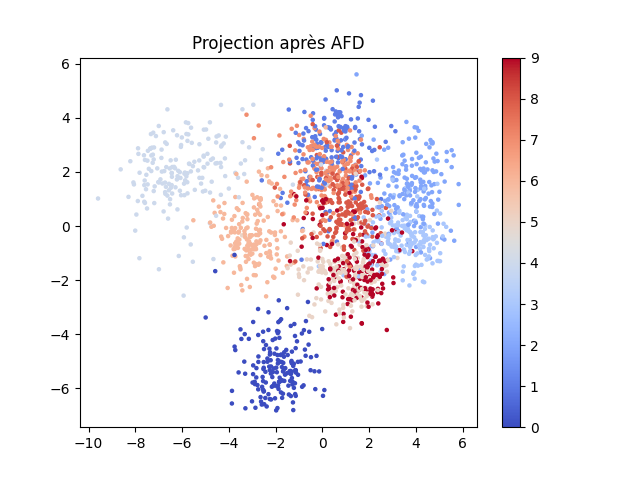
Classification par PMC linéare à une couche cachée¶
Pour comparaison, examinons d’abord les résultats obtenus avec un PMC linéaire à une couche cachée de 2 neurones :
from sklearn.neural_network import MLPClassifier
clf = MLPClassifier(hidden_layer_sizes=(2,), activation='identity', solver='adam', max_iter=5000, random_state=100)
clf.fit(X_train1, y_train1)
print("Matrice de poids entrées -> couche cachée : {}".format(clf.coefs_[0].shape))
print("Matrice de poids couche cachée -> sorties : {}".format(clf.coefs_[1].shape))
train_score = clf.score(X_train1, y_train1)
print("Le score en train est {}".format(train_score))
test_score = clf.score(X_test1, y_test1)
print("Le score en test est {}".format(test_score))
Comme dans le cas des auto-encodeurs, pour pouvoir afficher les activations des neurones de la couche cachée il faut refaire le calcul du réseau :
activationsLineaires_train1 = np.dot(X_train1,clf.coefs_[0]) + clf.intercepts_[0]
activationsLineaires_test1 = np.dot(X_test1,clf.coefs_[0]) + clf.intercepts_[0]
plt.figure()
plt.scatter(activationsLineaires_train1[:,0], activationsLineaires_train1[:,1], c=y_train1, cmap='coolwarm', s=5)
plt.scatter(activationsLineaires_test1[:,0], activationsLineaires_test1[:,1], c=y_test1, cmap='coolwarm', s=5)
plt.colorbar()
plt.title("Représentation dans MLP linéaire")
plt.show()
On constate que l’aspect des représentatins est relativement similaire à celui des projections sur les deux premiers axes discriminants (les deux sont liées par une transformation linéaire).
Classification par PMC non linéaire à plusieurs couches cachées¶
Question :
Employez un PMC à trois couches cachées de 40, 2 et respectivement 10 neurones et une fonction d’activation sigmoïde. Afin d’avoir une meilleure généralisation il peut être nécessaire d’augmenter le poids de la régularisation par weight decay. Examinez les représentations obtenues dans la couche cachée de 2 neurones, que constatez-vous?

