Cours - Réduction de dimension

Ce chapitre correspond à 2 séances de cours.

[Diapositives du cours]

Les supports écrits sont en cours de réalisation.

Réduction non-linéaire de dimension

Les jeux de données en haute dimension posent plusieurs problèmes lorsqu’il s’agit d’en faire une analyse descriptive. D’une part, lorsque le nombre de variables descriptives est grand, il est impossible de visualiser de façon satisfaisante ces données. D’autre part, le fléau de la dimension rend malaisée l’application des méthodes classiques de fouille de données à cause de l’éparsité des observations.

Une solution consiste à ne pas traiter la matrice d’observations originale mais plutôt à la remplacer par une représentation dans un espace de plus petite dimension, tout en conservant l’essentiel de l’information. Deux approches cohabitent :

• la sélection de variables, permettant d’éliminer les variables superflues et donc de réduire le nombre de colonnes de la matrice d’observations, qui est étudiée dans le chapitre sur la sélection de variables ;

• la réduction de dimension, qui remplace les variables originales par un nouveau jeu de variables plus petit, que nous allons voir ici.

En réalité, la réduction de dimension a déjà été abordée dans le chapitre concernant les méthodes factorielles. L’analyse en composantes principales (ACP) est un des exemples phares de la réduction de dimension : en projetant sur les \(k\) premières composantes principales, il est possible de réduire le nombre de variables décrivant un jeu de données \(\mathbf{X}\), tout en conservant le maximum de l’information (que l’on assimile dans ce cas à la variance).

Toutefois, les méthodes factorielles sont des techniques de réduction de dimension dites linéaires, c’est-à-dire que les variables de l’espace réduit \(\{y_1, y_2, \dots, y_q\} \in \mathcal{Y}\) sont des combinaisons linéaires des variables de l’espace de départ \(\{x_1, x_2, \dots, x_p\}\). Or, ceci limite grandement les possibilités de réduction de dimension.

Locally Linear Embedding

Considérons une matrice d’observations \(\mathbf{X}\) de dimensions \((n, p)\), c’est-à-dire à \(n\) observations (lignes) et \(p\) variables descriptives (colonnes). L’objectif de la réduction de dimension est de déterminer \(\mathbf{\hat{X}}\) de dimension \((n, q)\) avec \(q < p\) qui représente bien la structure de \(\mathbf{X}\). Par structure, on décide notamment de s’intéresser à la propriété suivante : deux observations réduites \({\mathbf{x}'}_i\) et \({\mathbf{x}'}_j\) sont voisines dans l’espace d’arrivée si et seulement si les observations associées \(\mathbf{x}_i\) et \(\mathbf{x}_j\) dans l’espace de départ sont également voisines. Autrement dit, on souhaite que notre réduction de dimension conserve la notion de voisinage entre les observations. Ce n’est pas le seul critère qui pourrait être imaginé pour conserver l’information contenue dans le jeu de données, mais c’est celui que nous allons utiliser en pratique.

L’algorithme Locally Linear Embedding ou LLE a été introduit par [RS00] en 2000. Le principe est le suivant : localement, le nuage d’observations \(\mathbf{X}\) peut être considéré comme linéaire, c’est-à-dire engendré par un sous-espace affine. En pratique, LLE considère que chaque observation \(\mathbf{x}_i \in \mathbf{X}\) peut-être reconstruite comme une moyenne pondérée de ses voisins \(\mathbf{x}_{j_1}, \mathbf{x}_{j_2}, \dots, \mathbf{x}_{j_k}\). Dans l’espace d’arrivée, l’observation réduite correspondante \(\mathbf{y}_i\) doit donc pouvoir être reconstruite par la même combinaison linéaire de ses propres voisins réduits \(\mathbf{y}_{j_1}, \mathbf{y}_{j_2}, \dots, \mathbf{y}_{j_k}\).

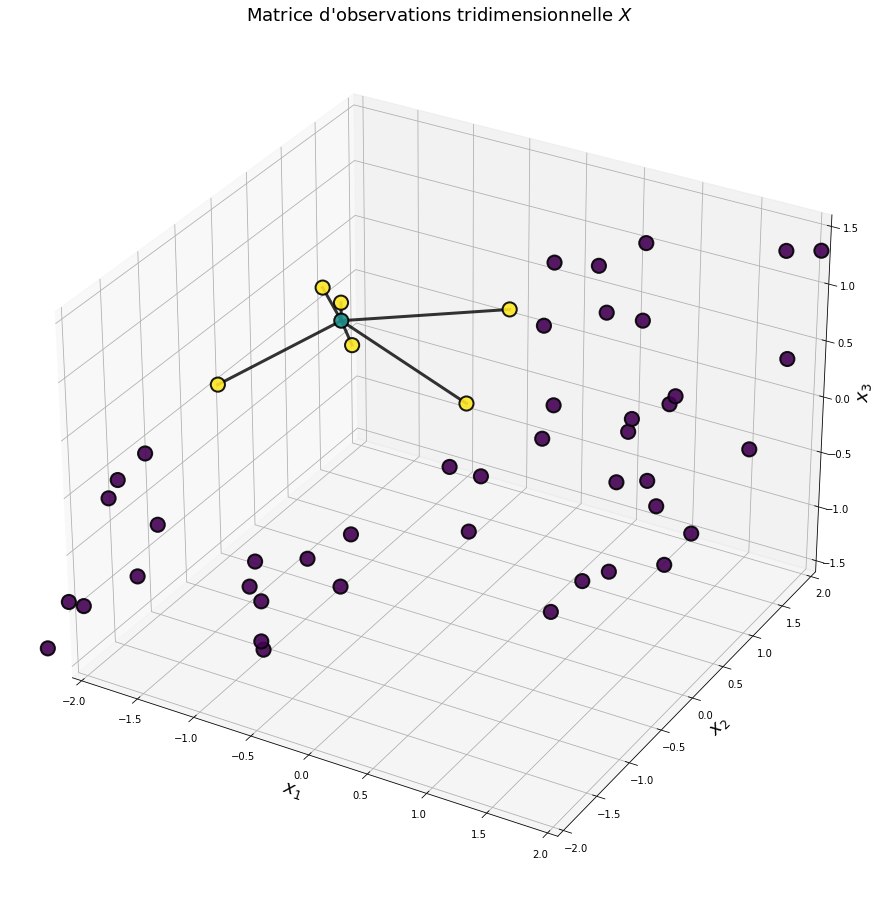
Fig. 107 Un nuage de points composé d’observations à 3 dimensions \(\mathbf{x} = (x_1, x_2, x_3)\). Considérons une observation particulière que l’on note \(\mathbf{x}^*\) (en bleu). Locally Linear Embedding suppose que cette observation peut se reconstruire comme une combinaison linéaire de ses voisins (en jaune) : \(\mathbf{x}^* = \sum_{j_l} w_{j_l} \mathbf{x}_{j_l}\). La première étape de LLE consiste à rechercher les valeurs \(w_{j_l}\) de pondération de cette combinaison linéaire.

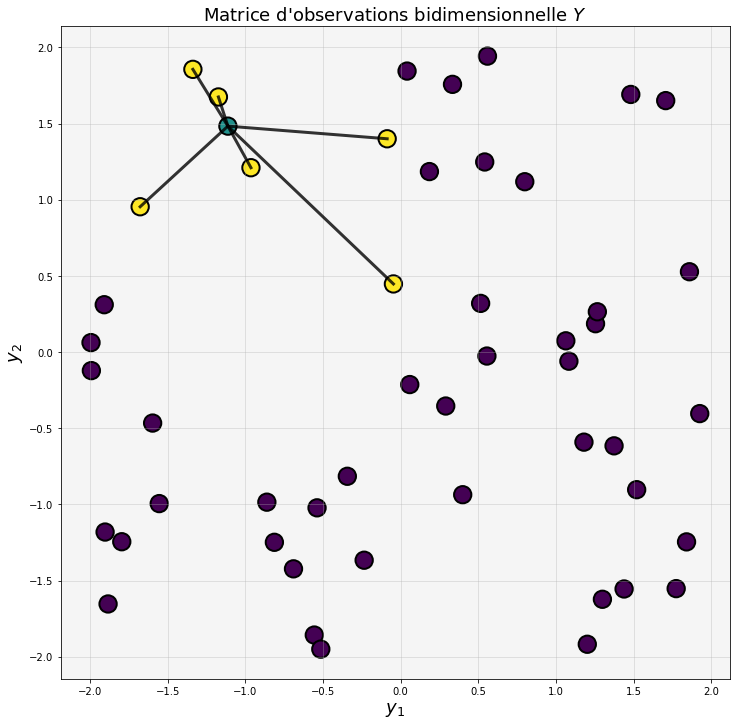
Fig. 108 Dans l’espace réduit à seulement deux dimensions, on cherche comment placer les voisins \(\mathbf{y}_{j_k}\) (en jaune) de l’observation correspondante \(\mathbf{y}^*\) (en bleu) de sorte à la reconstruire par la même combinaison linéaire. La deuxième étape de LLE consiste à déterminer les valeurs des coordonnées des observations réduites \(\mathbf{y}_i\) de sorte que \(\mathbf{y}^* \approx \sum_{j_l} w_{j_l} \mathbf{y}_{j_l}\). Les pondérations \(w_{j_l}\) sont les mêmes que celles déterminées à la première étape.

L’algorithme concret est donc le suivant :

1. Pour chaque point \(\mathbf{x}_i \in \mathbf{X} \subset \mathbb{R}^p\)

   • trouver ses \(k \geq 2\) plus proches voisins, notés \(V_i = \{\mathbf{x}_{j_1}, \mathbf{x}_{j_2}, \dots, \mathbf{x}_{j_k}\}\);

   • les plus proches voisins s’obtiennent en comparant les distances euclidiennes entre \(\mathbf{x}_i\) et chaque \(\mathbf{x}_j \in \mathbf{X}\).

2. Déterminer les coefficients permettant de reconstruire chaque observation par une combinaison linéaire de ses voisins, c’est-à-dire la matrice \(\mathbf{W}^*\) de dimensions \((n,n)\) telle que

   (46)\[\mathbf{W}^* = \arg\min_\mathbf{W} \sum_i \lVert \mathbf{x}_i - \sum_{\mathbf{x}_j \in V_i} w_{ij} \mathbf{x}_j \rVert_2^2\]

   avec la contrainte \(\sum_j w_{ij} = 1\).

3. Déterminer le nuage de points réduit représenté par la matrice \(\mathbf{Y}^* \subset \mathbb{R}^q\) qui minimise l’erreur quadratique de reconstruction, c’est-à-dire

   (47)\[\mathbf{Y}^* = \arg\min_\mathbf{Y} \sum_i \lVert \mathbf{y}_i - \sum_{\mathbf{y}_j \in V_i} w^*_{ij} \mathbf{y}_j \rVert_2^2\]

   ce qui revient déterminer les valeurs des coordonnées réduites des observations \(\mathbf{y}_i\) qui se reconstruisent par la même combinaison linéaire \(\mathbf{W}^*\) de leurs voisins.

Remarquons que dans l’équation (46), la matrice \(\mathbf{W}^*\) des pondérations qui minimise l’erreur de reconstruction est indépendante de l’échelle. En effet, multiplier toutes les coordonnées par une constante \(\lambda\) multiplie les distances par ce même facteur, mais ne change pas les relations de voisinages. Il existe donc une infinité de solutions possibles, toutes les matrices de type \(\lambda \mathbf{W}^*\). La contrainte \(\sum_j w_{ij} = 1\) permet d’assurer l’unicité de la solution.

Le problème décrit par l’équation (46) est un problème d’optimisation aux moindres carrés. Ce problème admet une solution analytique qui s’obtient directement à partir de la matrice de covariance locale calculée sur le \(k\)-voisinage de \(\mathbf{x}\).

Le problème décrit par l’équation (47) se résoud quant à lui par le calcul des vecteurs propres d’une matrice bien choisie, dépendant uniquement de \(\mathbf{W}\).

Pour plus de détails concernant ces deux étapes d’optimisation, consulter les annexes A et B de [SR00].

Illustration

Pour mieux comprendre l’effet de Locally Linear Embedding, nous pouvons prendre un exemple-jouet régulièrement utilisé en réduction de dimension. Le « Gâteau roulé » (ou Swiss Roll, roulé suisse) est un jeu de données contenant des observations en trois dimensions. Néanmoins, bien qu’en trois dimensions, ce jeu de données peut être « déroulé » sur un plan bidimensionnel. Il existe donc une représentation naturelle de ce jeu de données à trois variables dans une version à seulement deux variables.

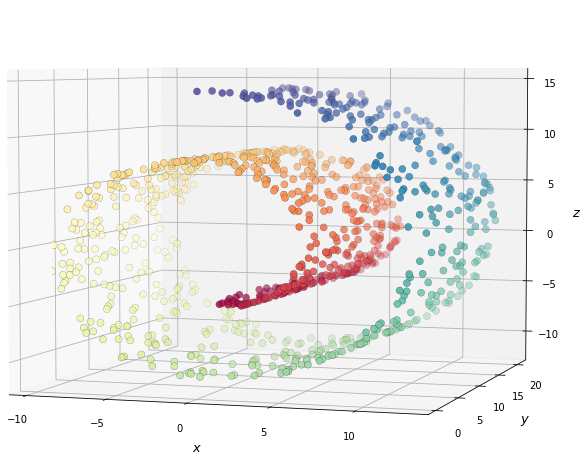
Fig. 109 Le jeu de données du « Gâteau roulé » (Swiss Roll) représente un rectangle 2D enroulé sur lui-même. Les couleurs permettent d’identifier les voisinages et ne sont présentes qu’à titre indicatif.

À titre de comparaison, nous pouvons appliquer une analyse en composantes principales (ACP) sur le Swiss Roll. Les directions qui expliquent le plus de variance sont néanmoins assez peu représentatives. En effet, la transformation qui permet de passer du gâteau roulé à trois dimensions à son alter ego déroulé n’est pas linéaire et l’ACP ne permet donc pas de construire une projection l’approchant.

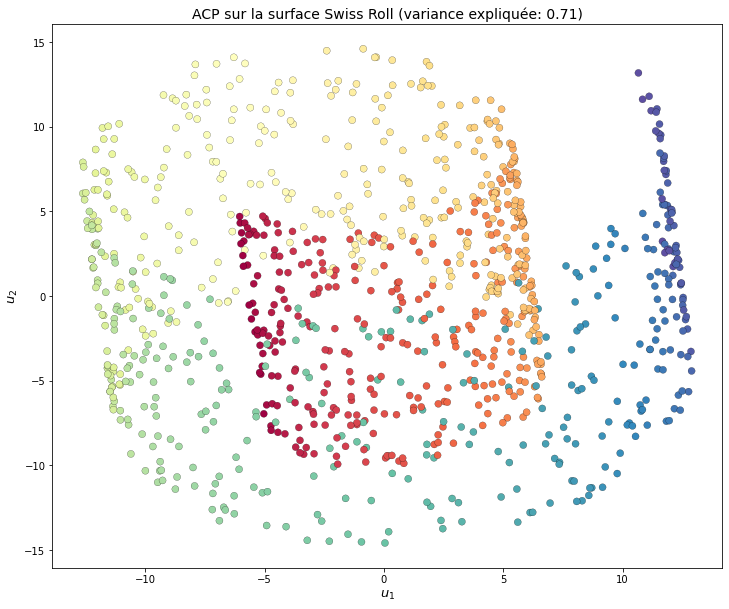
Fig. 110 L’analyse en composantes principales sur le gâteau roulé extrait les directions qui expliquent le plus la variance. La troisième dimension est masquée. Les voisins sont globalement peu préservés. La réduction de dimension « idéale » n’étant pas linéaire, l’ACP ne répond pas au besoin.

L’application de l’algorithme LLE permet toutefois d’obtenir une projection qui n’est que localement linéaire. Cet algorithme de réduction de dimension a donc une plus grande expressivité et permet de dérouler de façon satisfaisante le Swiss Roll. Par rapport à l’ACP, il est important de noter que LLE conserve les relations de voisinage : des observations voisines dans l’espace de départ demeurent voisines lorsqu’elles sont projetées dans l’espace réduit. Cette propriété est généralement celle que l’on cherche à conserver quand on s’intéresse à la réduction de dimension non-linéaire.

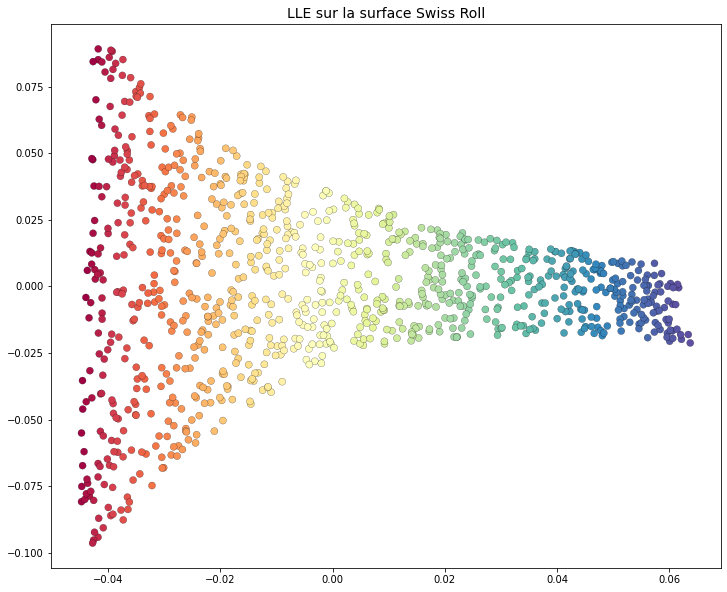
Fig. 111 L’application de Locally Linear Embedding permet de « dérouler » la surface du jeu de données. L’approche par voisinage permet de passer de proche en proche en respectant la structure locale (linéaire).

Le plongement dans l’espace à deux dimensions de la figure Fig. 111 illustre une notion particulièrement importante de la réduction non-linéaire de dimension. Notre objectif est de préserver la structure locale du jeu de données et, tout particulièrement, les relations de voisinage. LLE ne préserve donc pas les distances. C’est la raison pour laquelle nous observons cet effet « d’entonnoir ». Les points rouges sont plus éloignés les uns des autres que les points violets. Néanmoins, les voisinages sont invariants à l’échelle. Il n’y a donc aucune conclusion à en tirer. D’ailleurs, dans le roulé suisse de départ, les points rouges ne sont pas plus éloignés que les points bleus. Ce type de distorsion est fréquent dans les visualisations obtenues par LLE et ne doit pas être interprété comme représentatif de la structure des données. Seules les relations de voisinages (et donc la structure locale) est préservée par cet algorithme.

t-SNE : t-distributed Stochastic Neighbor Embedding

Représenter le voisinage d’un point par ses \(k\) plus proches voisins présente deux inconvénients. D’abord, là où les observations sont très denses les \(k\) plus proches voisins sont très proches alors que là où les observations sont peu denses les \(k\) plus proches voisins sont très éloignés, l’échelle des similarités conservées n’est pas du tout la même. Ensuite, cette séparation stricte entre voisins, pris en compte totalement, et non voisins, totalement ignorés, introduit des fragilités dans l’opération de réduction de dimension. Définir le voisinage par un rayon plutôt que par une valeur de \(k\) permet de conserver l’échelle et répond ainsi au premier inconvénient mais pas au second.

t-SNE [MH08] est un algorithme de réduction de dimension non-linéaire particulièrement populaire. Son principe général est similaire à celui de LLE : chercher un jeu de données dans un espace de dimension réduite qui présente les mêmes structures locales au voisinage de chaque point. Cependant, t-SNE généralise la notion de voisinage déterministe de LLE à une notion probabiliste. On cherchera non plus à conserver les voisins d’une observation, mais plutôt à conserver les probabilités que d’autres observations lui soient voisines. Nous présentons d’abord brièvement Stochastic Neighbor Embedding (SNE, [HR02]), qui introduit les idées principales, avant de décrire les évolutions présentes dans t-SNE.

Voisinages et probabilités : Stochastic Neighbor Embedding

Considérons une matrice d’observations \(\mathbf{X}\) de \(n\) observations de dimensions \(D\). Représentons le voisinage d’un point \(\mathbf{x}_i \in \mathbf{X}\) par une probabilité conditionnelle \(p_{j|i} = p(\mathbf{x}_j|\mathbf{x}_i)\) pour toute autre observation \(\mathbf{x}_j \in \mathbf{X}\), qu’on peut voir comme la probabilité que \(\mathbf{x}_j\) soit considéré un voisin de \(\mathbf{x}_i\). Cette valeur devra être entre 0 et 1 et décroître avec la distance entre \(\mathbf{x}_i\) et \(\mathbf{x}_j\). L’objectif de Stochastic Neighbor Embedding (SNE, [HR02]) est de déterminer le nuage de points représenté par les observations réduites \(\mathbf{y}_i\) de telle sorte que \(p(\mathbf{y}_j|\mathbf{y}_i) \simeq p(\mathbf{x}_j|\mathbf{x}_i)\) pour tous les couples \((i,j)\).

Dans SNE la valeur de \(p_{j|i}\) est définie de la façon suivante :

(48)\[p_{j|i} = p(\mathbf{x}_j|\mathbf{x}_i) = \frac{\exp(-\lVert \mathbf{x}_i - \mathbf{x}_j\rVert_2^2 / 2\sigma^2)}{\sum_{k\neq i} \exp(-\lVert \mathbf{x}_k - \mathbf{x}_i \rVert_2^2 / 2\sigma^2)}\]

avec par convention \(p_{i|i} = 0\) (\(\mathbf{x}_i\) n’est pas voisin de lui-même). Le dénominateur de l’équation (48) permet de normaliser les probabilités conditionnelles de sorte que \(\sum_j p_{j|i} = 1\) pour tout \(i\). Le numérateur correspond à la similarité entre \(\mathbf{x}_i\) et \(\mathbf{x}_j\), représentée par la valeur de la densité d’une gaussienne (ou loi normale) centrée en \(\mathbf{x}_i\). Intuitivement, cela revient donc à placer un noyau gaussien d’écart-type \(\sigma\) centré sur l’observation \(\mathbf{x}_i\). Plus \(\sigma\) est faible, plus la probabilité décroît rapidement avec la distance entre \(\mathbf{x}_i\) et \(\mathbf{x}_j\).

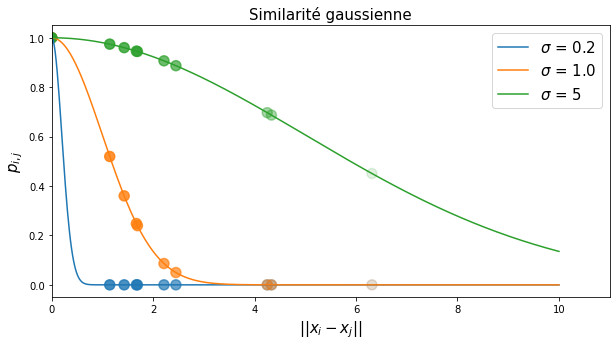
Fig. 112 Valeur de la similarité gausienne en fonction de la distance euclidienne entre \(\mathbf{x}_i\) et \(\mathbf{x}_j\).

Le choix de \(\sigma\) peut être fait en fonction du nombre approximatif de voisins qu’on souhaite considérer pour chaque observation. Une évaluation continue de ce nombre est donnée par la perplexité définie par

(49)\[Perp(P_i) = 2^{H(P_i)}\]

\(H(P_i)\) étant l’entropie de la distribution \(P_i\), qui augmente avec le rapprochement des valeurs des \(p_{j|i}\).

Nous pouvons constater que l’augmentation de \(\sigma\) mène à une augmentation de l’entropie \(H(P_i)\) (car la gaussienne s’aplatit) et donc de la perplexité. Cette proportionalité entre \(\sigma\) et \(Perp(P_i)\) fait que parfois c’est \(\sigma\) (ou \(\sigma^2\)) qui est appelé « perplexité » comme dans [HR02] p.7.

Comme pour LLE, nous cherchons donc désormais une matrice réduite \(\mathbf{Y}\), de dimension \(d < D\), de sorte que les probabilités conditionnelles \(q_{j|i} = p(\mathbf{y}_j|\mathbf{y}_i)\) soient les plus proches possible des \(p_{j|i}\). Ici les points \(\mathbf{y}_i\) sont les images des observations de départ \(\mathbf{x}_i\) dans l’espace de dimension réduite que nous appelons aussi espace d’arrivée. Dans SNE ces probabilités sont définies par

(50)\[q_{j|i} = p(\mathbf{y}_j|\mathbf{y}_i) = \frac{\exp(-\lVert \mathbf{y}_i - \mathbf{y}_j\rVert_2^2)}{\sum_{k\neq i} \exp(-\lVert \mathbf{y}_k - \mathbf{y}_i \rVert_2^2)}\]

ce qui revient à employer un noyau gaussien d’écart-type \(\sigma = \frac{1}{\sqrt{2}}\) dans l’espace d’arrivée. Une autre valeur de cet écart-type produirait simplement un changement d’échelle dans les résultats.

Une mesure usuelle de l’écart entre deux distributions de probabilité est la divergence de Kullback-Leibler. Si on note par \(P_i\) la distribution des probabilités conditionnelles dans l’espace de départ, \(p_{j|i}\), et par \(Q_i\) celle des probabilités conditionnelles dans l’espace d’arrivée, \(p_{j|i}\), la divergence de Kullback-Leibler entre les deux est

\[D_\text{KL}(P_i\|Q_i) = \sum_{j} p_{j|i} \log \frac{p_{j|i}}{q_{j|i}}\]

On peut montrer que cette mesure s’annule si et seulement si \(p_{j|i} = q_{j|i}\) pour tout \(j\).

SNE minimise la somme sur toutes les observations de ces divergences de Kullback-Leibler entre les distributions conditionnelles de l’espace de départ et celles de l’espace d’arrivée :

\[L = \sum_{i} D_\text{KL}(P_i\|Q_i) = \sum_{i} \sum_{j} p_{j|i} \log \frac{p_{j|i}}{q_{j|i}}\]

Cette minimisation est faite en utilisant la descente de gradient, une méthode itérative d’optimisation continue qui consiste à appliquer de petites modifications successives aux paramètres (ici les \(\mathbf{y}_i\)) du critère optimisé (ici \(L\)), dans le sens opposé au gradient du critère par rapport aux paramètres, jusqu’à l’atteinte d’un minimum de ce critère. Dans le chapitre Réseaux de neurones multicouches nous regardons de plus près la descente de gradient et son application aux réseaux de neurones.

De SNE à t-SNE

t-SNE a été introduit dans [MH08] pour pallier à deux insuffisances de SNE, la complexité du problème d’optimisation et l”« agglutinement ».

La première évolution est l’emploi dans t-SNE de distributions de probabilités jointes pour représenter les relations de voisinage et la minimisation d’une divergence de Kullback-Leibler unique entre ces distributions :

\[L_{t-SNE} = \sum_{i} D_\text{KL}(P\|Q) = \sum_{i} \sum_{j} p_{ij} \log \frac{p_{ij}}{q_{ij}}\]

où on considère encore que \(p_{ii} = q_{ii} = 0\). Les probabilités jointes dans l’espace d’arrivée (de dimension réduite) seraient ainsi obtenues par :

(51)\[q_{ij} = \frac{\exp(-\lVert \mathbf{y}_i - \mathbf{y}_j\rVert_2^2)}{\sum_{k\neq l} \exp(-\lVert \mathbf{y}_k - \mathbf{y}_l \rVert_2^2)}\]

On constate qu’au dénominateur la somme est faite sur toutes les paires de points distincts, afin de garantir la condition de normalisation.

Les auteurs considèrent que dans l’espace de départ l’équation equivalente engendre des difficultés pour bien contraindre la représentation des observations isolées et proposent plutôt d’employer

(52)\[p_{ij} = \frac{p_{i|j} + p_{j|i}}{2n}\]

où \(n\) est le nombre d’observations et les \(p_{i|j}, p_{j|i}\) sont obtenues par l’équation de SNE (48).

La seconde évolution introduite dans t-SNE vise à résoudre le problème de l”« agglutinement ». Examinons la signification de ce problème et la solution apportée dans t-SNE.

La gaussienne utilisée pour définir les \(p_{ij}\) et \(q_{ij}\) est à décroissance rapide. Cela permet de facilement distinguer les voisins (données proches de \(\mathbf{x}_i\)) des non-voisins, pour qui la similarité sera quasi-nulle compte-tenu de la queue « courte » de la gaussienne. Cette propriété est utile dans l’espace de départ mais moins dans l’espace d’arrivée. Afin de voir pourquoi, supposons que l’on souhaite projeter les données dans un plan, donc un espace à deux dimensions, pour la visualisation. Si l’on utilise une similarité gaussienne, alors les voisins sont agglutinés pour être dans la zone non-nulle de la gaussienne. En effet, pour un même nombre de points, il y a moins de « volume » disponible en 2D que dans un espace à \(n\) dimensions. Les points qui sont voisins se retrouvent placés très proches les uns des autres, tandis que les non-voisins peuvent être placés n’importe où ailleurs, puisque la similarité vaut de toute façon zéro. Autrement dit, en utilisant une similarité gaussienne dans l’espace d’arrivée, on risque de produire une visualisation avec de nombreux points qui se chevauchent, séparés par de grandes régions vides. On appelle ce problème « agglutinement » (ou crowding).

Pour éviter ce problème d’agglutinement, t-SNE emploie une autre définition de la probabilité conditionnelle dans l’espace réduit, qui encourage les points à se disperser dans le plan. Plutôt qu’employer une gaussienne (ou loi normale) comme dans l’équation (51), la similarité pour les observations réduites \(\mathbf{y}_i\) s’appuie alors sur une loi \(t\) (Student) à 1 degré de liberté (qui est d’ailleurs une loi de Cauchy) et s’écrit :

(53)\[q_{ij} = \frac{\left(1 + \lVert \mathbf{y}_i -\mathbf{y}_j \rVert_2^2\right)^{-1}}{\sum_{k \neq l} \left(1 + \lVert \mathbf{y}_k - \mathbf{y}_l \rVert_2 ^2\right)^{-1}}\]

avec par convention \(q_{i,i} = 0\).

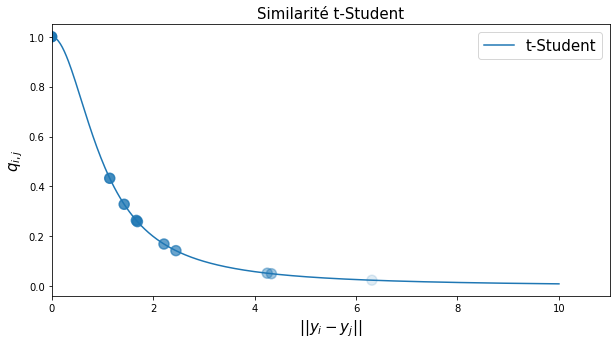
Fig. 113 Valeur de la similarité t (Student) en fonction de la distance euclidienne entre \(\mathbf{y}_i\) et \(\mathbf{y}_j\).

Cette fonction exhibe une décroissance assez rapide (mais moins rapide que la gaussienne) pour distinguer les voisins des non-voisins, mais surtout une queue longue, qui permet de mieux répartir les points dans l’espace d’arrivée, cf. Fig. 114.

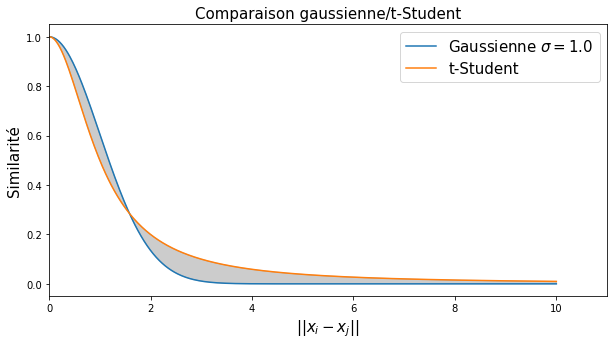
Fig. 114 Comparaison de la similarité gaussienne et la similarité Student.

Algorithme de t-SNE

Dans t-SNE, nous voulons rapprocher les distributions \(p_{i,j}\) et \(q_{i,j}\). Comme nous venons de le voir, il suffit de minimiser leur divergence de Kullback-Leibler pour atteindre cet objectif. Pour ce faire, nous pouvons utiliser un algorithme de descente de gradient sur les points \(\mathbf{y}_i\) :

1. Pour chaque paire de points \((\mathbf{x}_i, \mathbf{x}_j)\), calculer les probabilités suivant les équations (52) et (48).

2. Initialisation : Placer aléatoirement les \(n\) points réduits \(\mathbf{y}_1, \mathbf{y}_2, \dots, \mathbf{y}_n\) dans l’espace de dimension \(d\).

3. Tant que l’optimisation n’a pas convergé ou que le nombre maximal d’itérations n’est pas atteint :

   • Calculer les probabilités \(q_{i,j}\) par l’équation (51).

   • Calculer le gradient de la divergence de Kullback-Leibler par rapport à \(\mathbf{y}_i\) :

     \[\frac{\partial L_{t-SNE}}{\partial \mathbf{y}_i} = 4 \sum_j (p_{ij} - q_{ij})(\mathbf{y}_i - \mathbf{y}_j)(1 + \lVert \mathbf{y}_i - \mathbf{y}_j \rVert_2^2)^{-1}\]

   • Déplacer chaque point \(\mathbf{y}_i\) en suivant la plus forte pente dans le sens opposé au gradient (= descente de gradient) avec un pas \(\alpha > 0\) :

     \[\mathbf{y}_i := \mathbf{y}_i - \alpha \frac{\partial L_{t-SNE}}{\partial \mathbf{y}_i}\]

   • Fin tant que

Note

Le calcul permettant d’obtenir l’expression analytique du gradient de la fonction de coût, \(\frac{\partial L}{\partial \mathbf{y}_i}\), est détaillé dans l’annexe A de [MH08].

Autres fonctions de similarité

Remarquons que l’étape 1 de l’algorithme peut être ignorée s’il existe déjà une matrice de similarités \(\mathbf{S} = (p_{ij})\) pré-calculée sur le jeu de données. En pratique, il n’est donc pas indispensable d’utiliser la similarité gaussienne définie par (48). N’importe quelle métrique de similarité peut être employée pour construire la matrice des probabilités conditionnelles. Le module TSNE de Scikit-learn accepte notamment de nombreuses métriques, non nécessairement euclidiennes, et il est même possible de passer une matrice de similarité arbitraire précalculée. Cela peut être utile pour appliquer t-SNE sur des données mixtes, en utilisant une fonction ad hoc capable notamment de définir une similarité pour des variables non quantitatives.

Initialisation de t-SNE

Comme toutes les méthodes par descente de gradient, l’algorithme d’optimisation de t-SNE est sensible à son initialisation. Le placement initial des points \(\mathbf{y}_i\) étant aléatoire, les résultats obtenus par application de t-SNE peuvent fortement varier d’une exécution à une autre. Par ailleurs, t-SNE ne préserve que les voisinages. C’est donc un algorithme qui se concentre sur la structure locale, au détriment de la préservation de la structure globale.

Pour pallier ces deux limitations, une alternative consiste à appliquer d’abord une analyse en composantes principales et conserver seulement les \(d\) premières composantes. Le nuage de points projeté peut ainsi servir d’initialisation aux observations réduites \(\mathbf{y}_i^0\) avant la phase d’optimisation par descente de gradient. D’un” point de vue théorique, cette initialisation a deux avantages :

1. Une meilleure préservation de la structure globale grâce à l’ACP.

2. Une plus grande reproductibilité en supprimant la stochasticité liée à l’initialisation.

En pratique, cette initialisation est plus robuste et elle est généralement appliquée par défaut dans les bibliothèques qui implémentent t-SNE.

Choix de la valeur de perplexité

La perplexité est le principal paramètre à régler lors de l’application de t-SNE.

Une perplexité faible restreint fortement les observations qui sont définies comme voisines l’une de l’autre. Seules des observations très proches peuvent avoir une similarité non-nulle. Cela accentue la préservation de la structure locale au détriment de la structure globale. À l’inverse, une perplexité élevée inclut presque toutes les observations dans le voisinage de toutes les autres, à l’exception des plus éloignées. Cela permet ainsi de mieux capturer la structure globale du nuage de points, au détriment des détails locaux, comme illustré dans la Fig. 115.

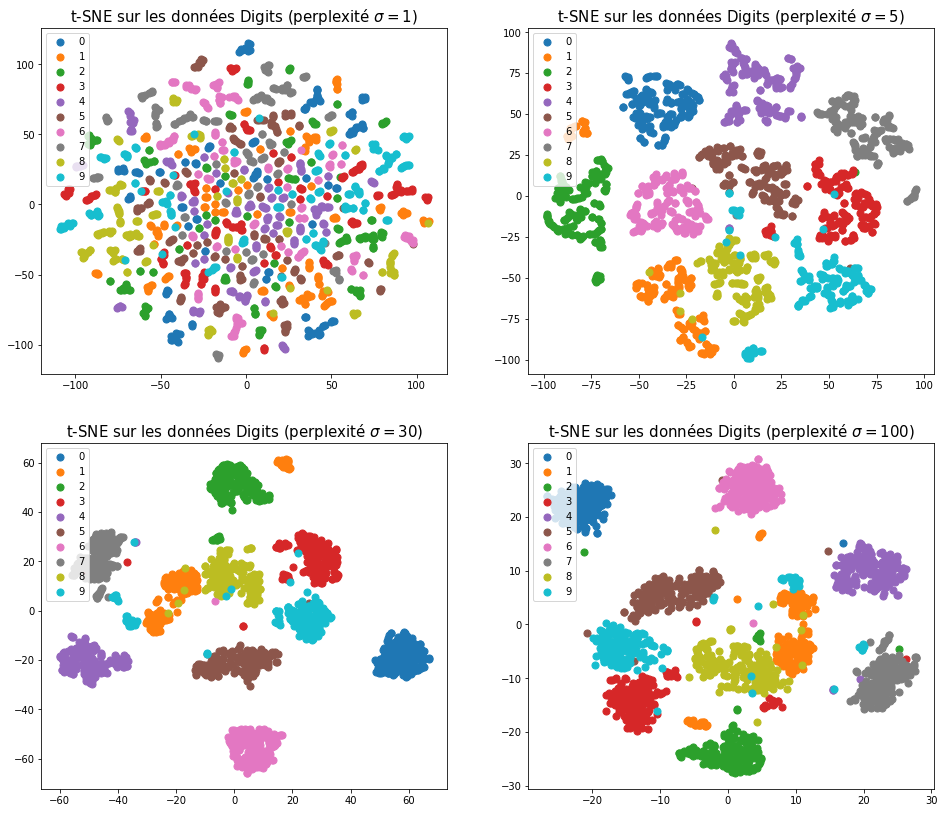
Fig. 115 Application de t-SNE sur le jeu de données Digits pour différentes valeurs de perplexité.

En pratique, il est recommandé d’expérimenter plusieurs valeurs de perplexité et de croiser les interprétations au niveau local et au niveau global.

Optimisation

L’algorithme décrit plus haut pour t-SNE passe sous silence une astuce d’implémentation qui permet d’accélérer la convergence de la descente de gradient. En pratique, t-SNE est implémenté en deux phases :

1. Une phase dite d’exagération précoce (early exaggeration), durant laquelle toutes les probabilités conditionnelles \(p_{ij}\) dans l’espace initial sont multipliées par un facteur \(\gamma\). Cela permet d’augmenter artificiellement la séparation des groupes naturellement présents dans les données et de placer plus rapidement les observations réduites \(\mathbf{y}_i\) près de leur position optimale.

2. Une phase d’optimisation finale durant laquelle les valeurs réelles des probabilités conditionnelles sont utilisées, pour affiner le placement des observations réduites localement au sein de chaque groupe.

Des heuristiques plus ou moins sophistiquées existent afin de déterminer les valeurs des paramètres d’exagération et du pas d’apprentissage, comme celles décrites dans [BCA19]. Il n’est généralement pas utile de modifier ces paramètres.

En pratique, l’exagération précoce est appliquée pendant 250 itérations de la descente de gradient, puis l’optimisation se poursuit avec les valeurs normales des probabilités conditionnelles jusqu’à atteindre le critère d’arrêt (convergence ou nombre d’itérations maximal).

Pour mieux appréhender la flexibilité mais aussi les possibles erreurs d’interprétation des visualisations obtenues vec t-SNE il est utile de regarder les expériences proposées sur ce site.

UMAP : Uniform Manifold Approximation and Projection for Dimension Reduction

UMAP (Uniform Manifold Approximation & Projection) [MHM18] est un algorithme de réduction non-linéaire de dimension dont le principe est semblable à celui de t-SNE. Comme précédemment, nous recherchons une représentation des données en plus faible dimension qui présente la même topologie que le nuage des observations dans l’espace de départ. Pour ce faire, nous construisons une matrice des similarités entre les points dans l’espace de départ, puis nous cherchons l’ensemble des points dans l’espace d’arrivée qui vérifie le même graphe de similarité. La principale différence entre t-SNE et UMAP vient de leur définition de cette notion de similarité.

Similarité dans l’espace de départ

La similarité \(p_{i,j}\) entre deux observations différentes \(\mathbf{x}_i\) et \(\mathbf{x}_j\) est définie comme étant :

(54)\[ p_{i,j} = \exp\left(-\frac{\lVert \mathbf{x}_i - \mathbf{x}_j\rVert_2 -\rho_i}{\sigma_i}\right)\]

• \(\rho_i\) est la distance entre \(\mathbf{x}_i\) et son plus proche voisin : \(\rho_i = \min_{j \neq i} \lVert \mathbf{x}_i - \mathbf{x}_j \rVert_2\)

• \(\sigma_i\) est fixé de sorte que :

(55)\[ \sum_{j=1}^k \exp\left(- \frac{\max(0, \lVert \mathbf{x}_i - \mathbf{x}_j\rVert_2 - \rho_i)}{\sigma_i}\right) = \log_2 (k)\]

• \(k\) est un paramètre réglant le nombre de plus proches voisins à considérer, c’est-à-dire la taille du voisinage envisagé.

Cette similarité s’appuye donc sur un écart-type adaptatif pour le noyau gaussien, avec deux différences par rapport à t-SNE :

• la similarité ne commence à décroître qu’au-delà du plus proche voisin (lorsque la distance \(d(\mathbf{x}_i, \mathbf{x}_j) > \rho_i\)),

• la largeur du noyau (\(\sigma\)) dépend de la densité du voisinage : pour une même valeur de \(k\), dans un voisinage dense (beaucoup de points sont très proches de \(\mathbf{x}_i\)) l’équation (55) indique que la valeur de \(\sigma_i\) doit être plus faible que si le voisinage avait été moins dense (voisins plus éloignés de \(\mathbf{x}_i\)).

Note

Nous employons ici des notations \(p\) pour des similarités afin de les mettre en relation avec les mesures correspondantes dans t-SNE. Mais pour UMAP ces similarités ne sont pas des probabilités car les conditions de normalisation ne sont pas respectées.

Pour deux points \(\mathbf{x}_i\) et \(\mathbf{x}_j\), la similarité jointe \(p_{ij}\) devrait être symétrique (\(p_{ij} = p_{ji}\)). Dans UMAP cette symétrisation est obtenue grâce à la définition suivante :

\[p_{ij} = p_{i,j} + p_{j,i} - p_{i,j} \cdot p_{j,i}\]

La symétrisation est nécessaire car \(\rho_i \neq \rho_j\). Pour rappel, t-SNE utilise une autre symétrisation : \(p_{ij} = \frac{p_{i|j} + p_{j|i}}{2n}\).

Similarité dans l’espace d’arrivée

Comme pour t-SNE, on souhaite éviter l’agglutinement des points dans l’espace d’arrivée : de faibles variations de similarité dans l’espace de départ doivent correspondre à des variations plus significatives de distance dans l’espace d’arrivée. Cela revient à s’appuyer sur une distribution à queue épaisse pour définir les similarités dans l’espace d’arrivée.

La solution adoptée par UMAP consiste à s’inspirer de la loi \(t\) de Student pour définir la similarité dans l’espace d’arrivée :

\[q_{ij} = \frac{1}{1 + a \|\mathbf{y}_i - \mathbf{y}_j\|^{2b}}\]

\(a\) et \(b\) étant des paramètres réglables. En pratique, la fonction idéale n’autoriserait jamais deux points dans l’espace d’arrivée à être plus proches qu’une certaine distance minimale min_dist. Sur le segment \([0, \text{min_dist}]\) la similarité serait considérée comme égale à 1, ensuite on tolérerait une décroissance exponentielle douce de la similarité. Cela correspond à une fonction définie par morceaux :

\[\begin{split}\begin{cases} 1 & \text{si}~ \|\mathbf{y}_i - \mathbf{y}_j\| \leq \text{min_dist}\\ e^{-\|\mathbf{y}_i - \mathbf{y}_j\|} & \text{si}~ \|\mathbf{y}_i - \mathbf{y}_j\| > \text{min_dist}\\ \end{cases}\end{split}\]

En pratique, c’est le paramètre min_dist que l’on peut régler dans UMAP. Dans la définition de la similarité, le choix des paramètres \(a\) et \(b\) est ainsi fait automatiquement de sorte que la similarité qui en résulte soit la plus proche possible de cette fonction idéale définie par morceaux.

Optimisation

L’objectif est de trouver les points \(\mathbf{y}_i\) dans l’espace d’arrivée tels que les similarités \(q_{ij}\) s’approchent le plus possibles des similarités \(p_{ij}\). Autrement dit, on souhaite faire tendre les similarités \(q\) vers les similarités \(p\).

Pour UMAP cela est réalisé en minimsant une fonction objectif d’entropie croisée floue (fuzzy cross-entropy), qui mesure l’écart entre les deux distributions de similarités \(p\) et \(p\) :

(56)\[ \operatorname{CE}(X, Y) = \sum_{i=1}^n \sum_{j=1}^n \left[ p_{ij} \log\left(\frac{p_{ij}}{q_{ij}}\right) + (1 - p_{ij}) \log\left(\frac{1 - p_{ij}}{1 - q_{ij}}\right) \right]\]

L’entropie croisée floue est une extension de l’entropie croisée (définie au départ pour mesurer l’écart entre distributions de probabilités) au cas où les valeurs considérées (les \(p_{ij}\) et \(q_{ij}\)) sont individuellement entre 0 et 1 mais ne respectent pas les conditions de normalisation.

En développant les logarithmes, cette fonction objectif peut être écrite :

(57)\[\begin{split} \operatorname{CE}(X, Y) = \sum_{i=1}^n \sum_{j=1}^n \left[ p_{ij} \log p_{ij} + (1 - p_{ij}) \log\left(1 - p_{ij}\right) \right] \\ - \sum_{i=1}^n \sum_{j=1}^n \left[ p_{ij} \log q_{ij} + (1 - p_{ij}) \log\left(1 - q_{ij}\right) \right]\end{split}\]

Le premier terme dépend uniquement des données de l’espace de départ et ne peut donc pas être modifié. Pour minimiser l’entropie croisée floue, seul le second terme est donc minimisé en modifiant les \(\mathbf{y}_i\) (les projections dans l’espace d’arrivée) et donc les \(q_{ij}\).

Contrairement à t-SNE qui minimise la fonction objectif par descente de gradient directe en calculant la fonction à optimiser sur l’ensemble des données, UMAP accélère le calcul en réalisant une descente de gradient stochastique et estime l’entropie croisée sur un échantillon de quelques dizaines ou quelques centaines de points. L’échantillon est construit de sorte à contenir un mélange de voisins (\(p_{ij} \simeq 1\)) et de non-voisins (\(p_{ij} \simeq 0\)) afin d’optimiser simultanément les composantes de l’entropie croisée.

La mise à jour des points dans l’espace d’arrivée se fait (de manière analogue à t-SNE) par :

\[\mathbf{y}_i := \mathbf{y}_i - \alpha \frac{\partial \text{CE}}{\partial \mathbf{y}_i}\]

où \(\alpha\) est le pas d’apprentissage de l’algorithme de descente de gradient. Le gradient \(\frac{\partial \text{CE}}{\partial \mathbf{y}_i}\) dispose d’une expression analytique.

Réduction de dimension semi-supervisée

Une contribution intéressante en pratique de UMAP est l’extension de la notion de similarité pour prendre en compte d’éventuelles connaissances a priori sur les données. Considérons un jeu de données contenant des {étiquettes de groupes: \(\mathcal{X} = \{(\mathbf{x}_1, l_1), \dots, (\mathbf{x}_n, l_n)\}\) avec \(\mathbf{x}_i\) les observations et \(l_i\) les étiquettes (variable catégorielle).

Pour inclure la connaissance des étiquettes dans l’algorithme, UMAP définit une distance mixte sur le couple \((\mathbf{x}_i, l_i)\) :

\[\begin{split}d^\text{classe}(\mathbf{x}_i, \mathbf{x}_j) = \begin{cases} 0 ~\text{si}~ l_i = l_j\\ 0.5 ~\text{si}~ l_i ~\text{ou}~ l_j ~\text{est inconnue}\\ 1 ~\text{si}~ l_i \neq l_j\\ \end{cases}\end{split}\]

La distance totale impliquée dans le calcul des similarités entre points dans l’espace de départ est une somme pondérée par un paramètre \(\lambda\) :

\[d(\mathbf{x}_i, \mathbf{x}_j) = (1 - \lambda) d^\text{obs}(\mathbf{x}_i, \mathbf{x}_j) + \lambda d^\text{classe}(\mathbf{x}_i, \mathbf{x}_j)\]

où \(d^\text{obs}\) représente la distance habituelle dans l’espace de départ, qui s’applique sur les données \(\mathbf{x}_i\). Typiquement, dans la définition précédente, \(d^\text{obs}(\mathbf{x}_i, \mathbf{x}_j) = \lVert \mathbf{x}_i - \mathbf{x}_j \rVert_2\) (la distance euclidienne).

Cette nouvelle distance remplace ainsi la distance euclidienne dans (54).

Le paramètre \(\lambda\) permet de contrôler l’importance donnée à la sémantique ou aux données :

• si \(\lambda = 0\) alors seule la distance entre les données \(\mathbf{x}_i\) est prise en compte

• si \(0 < \lambda < 1\) alors la distance totale est une moyenne pondérée entre la distance entre les observations et entre les étiquettes. Par défaut, \(\lambda = 0.5\) et il s’agit d’une moyenne équilibrée.

• si \(\lambda = 1\) alors seule la distance entre les étiquettes est prise en compte.

---

[BCA19]

A.C. Belkina, C. O. Ciccolella, R. Anno, R. Halpert, J. Spidlen, et J. E. Snyder-Cappione. Automated optimized parameters for T-distributed stochastic neighbor embedding improve visualization and analysis of large datasets. Nature Communications. 10(1):5415, Nov. 2019.

[HR02] (1,2,3)

G.E. Hinton et S.T. Roweis. Stochastic Neighbor Embedding. In Advances in Neural Information Processing Systems, volume 15, pages 833-840, Cambridge, MA, USA, 2002. The MIT Press.

[MH08] (1,2,3)

Laurens van der Maaten et Geoffrey Hinton. Visualizing Data using t-SNE. Journal of Machine Learning Research. 9(86):2579-2605, Nov. 2008.

[MHM18]

Lawrence McInnes, John Healy et James Melville. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv:1802.03426, 2018.

[RS00]

Sam T. Roweis et Lawrence K. Saul. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science, 290:2323-2326, Dec. 2000.

[SR00]

Lawrence K. Saul et Sam T. Roweis. An Introduction to Locally Linear Embedding, 2000.