TP 2 - Deep Learning avec Keras et Manifold Untangling

L’objectif de cette seconde séance de travaux pratiques est de prendre en main la laibrairie Keras https://keras.io/ pour utiliser et entraîner des réseaux de neurones profonds. On analysera également les espaces de représentation appris par les modèles.

Avec Keras, les réseaux de neurones avec une structure de chaîne (réseaux « feedforward »), s’utilisent de la manière suivante:

from keras.models import Sequential
model = Sequential()

On créé ainsi un réseau de neurones vide. On peut alors ajouter des couches avec la fonction add.

On utilisera les données de la base MNIST, voir l’exercice 0 de la séance précédente pour les récupérer : tpbackprop.html.

Exercice 1 : Régression Logistique avec Keras

Par exemple, l’ajout d’une couche de projection linéaire (couche complètement connectée) de taille 10, suivi de l’ajout d’une couche d’activation de type softmax, peuvent s’effectuer de la manière suivante:

from keras.layers import Dense, Activation
model.add(Dense(10,  input_dim=784, name='fc1'))
model.add(Activation('softmax'))

On peut ensuite visualiser l’architecture du réseau avec la méthode summary() du modèle.

Question :

Quel modèle de prédiction reconnaissez-vous ? Vérifier le nombre de paramètres du réseau à apprendre dans la méthode summary(). - Écrire un script exo1.py permettant de créer le réseau de neurone ci-dessus.

Avec Keras, on va compiler le modèle en lui passant un loss (ici l” entropie croisée), une méthode d’optimisation (ici uns descente de gradient stochastique, stochatic gradient descent, sgd), et une métrique d’évaluation (ici le taux de bonne prédiction des catégories, accuracy):

from keras.optimizers import SGD
learning_rate = 0.1
sgd = SGD(learning_rate)
model.compile(loss='categorical_crossentropy',optimizer=sgd,metrics=['accuracy'])

Enfin, l’apprentissage du modèle sur des données d’apprentissage est mis en place avec la méthode fit :

from keras.utils import np_utils
batch_size = 100
nb_epoch = 20
# convert class vectors to binary class matrices
Y_train = np_utils.to_categorical(y_train, 10)
Y_test = np_utils.to_categorical(y_test, 10)
model.fit(X_train, Y_train,batch_size=batch_size, epochs=nb_epoch,verbose=1)

  • batch_size correspond au nombre d’exemples utilisé pour estimer le gradient de la fonction de coût.

  • epochs est le nombre d’époques (i.e. passages sur l’ensemble des exemples de la base d’apprentissage) lors de la descente de gradient.

N.B : on rappelle que comme dans les TME précédents, les labels données par la supervision doivent être au format « one-hot encoding ».

On peut ensuite évaluer les performances du modèle dur l’ensemble de test avec la fonction evaluate

scores = model.evaluate(X_test, Y_test, verbose=0)
print("%s: %.2f%%" % (model.metrics_names[0], scores[0]*100))
print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))

Le premier élément de score renvoie la fonction de coût sur la base de test, le second élément renvoie le taux de bonne détection (accuracy).

  • Implémenter l’apprentissage du modèle sur la base de train de la base MNIST.

  • Évaluer les performances du réseau sur la base de test et les comparer à celles obtenues lors de la séance précédente (ré-implémentation manuelle de l’algorithme de rétro-propagation). Conclure.

Exercice 2 : Perceptron avec Keras

On va maintenant enrichir le modèle de régression logistique en créant une couche de neurones cachée complètement connectée supplémentaire, suivie d’une fonction d’activation non linéaire de type sigmoïde. On va ainsi obtenir un réseau de neurones à une couche cachée, le Perceptron (cf séance précédente).

Écrire un script exo2.py pour mettre en place le Perceptron.

On ajoutera à un réseau séquentiel vide une première couche cachée de la manière suivante avec Keras :

model.add(Dense(100,  input_dim=784, name='fc1'))

Puis une non-linéarité de type sigmoïde :

model.add(Activation('sigmoid'))

Compléter le script exo2.py pour obtenir la couche de sortie à 10 classes suivie de la fonction d’activation soft-max. N.B : La dimension d’entrée n’a besoin d’être fournie que pour la couche d’entrée.

Question :

Quel est maintenant le nombre de paramètres du modèle MLP ? Justifier le calcul et le vérifier avec la méthode summary().

Une fois le modèle MLP créé, la façon de l’entraîner va être strictement identique à ce qui a été écrit dans l’exercice précédent, l’algorithme de rétro-propagation du gradient de l’erreur permettant de mettre à jour l’ensemble des paramètres du réseau.

  • Compléter le script exo2.py afin d’effectuer l’entraînement du réseau MLP.

  • Évaluer les performances du réseau sur la base de test et les comparer à celles obtenues lors de la séance précédente. Conclure.

  • Observer la documentation Keras pour voir la façon dont les paramètres du modèles sont initialisés dans les différentes couches.

  • On pourra utiliser la méthode suivante pour sauvegarder le modèle appris :

from keras.models import model_from_yaml
def saveModel(model, savename):
  # serialize model to YAML
  model_yaml = model.to_yaml()
  with open(savename+".yaml", "w") as yaml_file:
    yaml_file.write(model_yaml)
    print("Yaml Model ",savename,".yaml saved to disk")
  # serialize weights to HDF5
  model.save_weights(savename+".h5")
  print("Weights ",savename,".h5 saved to disk")

Exercice 3 : Réseaux de neurones convolutifs avec Keras

On va maintenant étendre le perceptron de l’exercice précédent pour mettre en place un réseau de neurones convolutif profond, « Convolutionnal Neural Networks », ConvNets.

Écrire un script exo3.py pour mettre en place un ConvNet.

Les réseaux convolutifs manipulent des images multi-dimensionnelles en entrée (tenseurs). On va donc commencer par reformater les données d’entrée afin que chaque exemple soit de taille \(28 \times 28 \times 1\).

x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
input_shape = (28, 28, 1)

Par rapport aux réseaux complètement connectés, les réseaux convolutifs utilisent les briques élémentaires suivantes :

1. Des couches de convolution, qui transforment un tenseur d’entrée de taille \(n_x \times n_y \times p\) en un tenseur de sortie \(n_{x'} \times n_{y'} \times n_H\), où \(n_H\) est le nombre de filtres choisi. Par exemple, une couche de convolution pour traiter les images d’entrée de MNIST peut être créée de la manière suivante :

from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.layers import Conv2D, MaxPooling2D
conv1 = Conv2D(32,kernel_size=(5, 5),activation='relu',input_shape=(28, 28, 1),padding='valid')

  • 32 est le nombre de filtres.

  • (5, 5) est la taille spatiale de chaque filtre (masque de convolution).

  • padding=”valid” correspond ignorer les bords lors du calcul (et donc à diminuer la taille spatiale en sortie de la convolution).

  • N.B. : on peut directement inclure dans la couche de convolution la non-linéarité en sortie de la convolution, comme illustré ici dans l’exemple avec une fonction d’activation de type relu.

  1. Des couches d’agrégation spatiale (pooling), afin de permettre une invariance aux translations locales. Voici par exemple la manière de déclarer une couche de max-pooling:

pool1 = MaxPooling2D(pool_size=(2, 2))

  • (2, 2) est la taille spatiale sur laquelle l’opération d’agrégation est effectuée.

  • N.B. : par défaut, le pooling est effectué avec un décalage de 2 neurones, dans l’exemple précédent on obtient donc des cartes de sorties avec des tailles spatiales divisées par deux par rapport à la taille d’entrée.

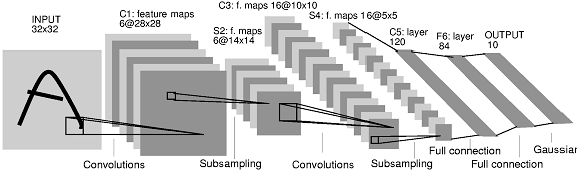
Compléter le script exo3.py pour mettre en place un ConvNet à l’architecture suivante, proche du modèle historique LeNet5 [LBD+89] et montré ci-dessous:

  • Une couche de convolution avec 16 filtres de taille \(5 \times 5\), suivie d’une non linéarité de type relu puis d’une couche de max pooling de taille \(2 \times 2\).

  • Une seconde couche de convolution avec 32 filtres de taille \(5 \times 5\), suivie d’une non linéarité de type relu puis d’une couche de max pooling de taille \(2 \times 2\).

  • Comme dans le réseau LeNet, on considérera la sortie du second bloc convolutif comme un vecteur, ce que revient à « mettre à plat » les couches convolutives précédentes (model.add(Flatten())).

  • Une couche complètement connectée de taille 100, suivie d’une non linéarité de type sigmoïde.

  • Une couche complètement connectée de taille 10, suivie d’une non linéarité de type softmax.

_images/LeNet5.png

  • Apprendre le modèle et évaluer les performances du réseau sur la base de test. Vous devez obtenir un score de l’ordre de 99% pour ce modèle ConvNet.

  • Quelle est le temps d’une époque avec ce modèle convolutif ?

  • On pourra sauvegarder le modèle appris avec la méthode saveModel précédente

Apprentissage sur GPU

  • Quelle est le temps d’une époque avec ce modèle convolutif ?

  • Vous pourrez tester l’apprentissage sur carte graphique du modèle, et comparer le temps d’entraînement

Exercice 4 : Visualisation avec t-SNE

On va maintenant illustrer la capacité des réseaux de neurones profonds à apprendre des représentations internes capables de résoudre le problème connu sous le nom de « manifold untangling » en neuroscience, c’est à dire de séparer les exemples des différentes classes dans l’espace de représentations appris.

Pour cela, on va utiliser des outils de visualisation qui vont vont permettre de représenter chaque donnée (par exemple une image de la base MNIST) par un point dans l’espace 2D. Ces même outils vont permettre de projeter en 2D les représentations internes des réseaux de neurones, ce qui va permettre d’analyser la séparabilité des points et des classes dans l’espace d’entrée et dans les espaces de représentions appris par les modèles.

On aura besoin des modules suivants qu’on pourra importer en début de script :

import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
from scipy.spatial import ConvexHull
from sklearn.mixture import GaussianMixture
from scipy import linalg
from sklearn.neighbors import NearestNeighbors
from sklearn.manifold import TSNE

La méthode t-Distributed Stochastic Neighbor Embedding (t-SNE) [vdMH08] est une réduction de dimension non linéaire, dont l’objectif est d’assurer que des points proches dans l’espace de départ présentent des positions proches dans l’espace (2D) projeté. Dit autrement, la mesure de distance entre points dans l’espace 2D doit refléter la mesure de distance dans l’espace initial.

On va appliquer la méthode t-SNE sur les données brutes de la base de test de MNIST en utilisant la classe TSNE du module sklearn.manifold : http://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html .

Créer un script exo1.py dont l’objectif va être d’effectuer une réduction de dimension en 2D des données de la base de test de MNIST en utilisant la méthode t-SNE.

  • Créer une instance de type TSNE. N.B : on choisira 2 composantes et les paramètres suivants : init='pca' (réduire la dimension préalablement avec une ACP), perplexity=30 (lié au nombre de voisins dans le calcul des distances), verbose=2 (pour l’affichage lors de l’apprentissage).

  • Appliquer la transformation pour obtenir les données projetées en 2D (fonction fit_transform). N.B : essayer tout d’abord avec un sous-ensemble de la base (e.g. 1000 exemples) pour tester l’algorithme, l’apprentissage avec l’ensemble de la base de test pouvant être long.

Métrique de séparation des classes

On va maintenant compléter le script exo4.py précédent afin de visualiser l’ensemble des points projetés en 2D, et de définir des critères pour analyser la séparabilité des classes dans l’espace projeté.

1. Calcul de l’enveloppe convexe des points projetés pour chacune des classe classe. On utilisera pour cela la la classe ConvexHull du module scipy.spatial https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.ConvexHull.html. Sur la base MNIST, on pourra donc utiliser le code suivant pour calculer les enveloppes convexes des points pour les 10 classes :

def convexHulls(points, labels):
  # computing convex hulls for a set of points with asscoiated labels
  convex_hulls = []
  for i in range(10):
    convex_hulls.append(ConvexHull(points[labels==i,:]))
  return convex_hulls
# Function Call
convex_hulls= convexHulls(x2d, labels)

où points (resp. labels) dans la méthode convexHulls(points, labels) correspond aux images projetées dans le plan 2D avec la méthode t-SNE de l’exercice 1 (resp. aux labels, i.e. classes, des images).

2. Calcul de l’ellipse de meilleure approximation des points. On utilisera pour cela la classe GaussianMixture du module sklearn.mixture http://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html#sklearn.mixture.GaussianMixture. On pourra donc utiliser le code suivant pour calculer les ellipses de meilleure approximation pour les 10 classes :

def best_ellipses(points, labels):
  # computing best fiiting ellipse for a set of points with asscoiated labels
  gaussians = []
  for i in range(10):
    gaussians.append(GaussianMixture(n_components=1, covariance_type='full').fit(points[labels==i, :]))
  return gaussians
# Function Call
ellipses = best_ellipses(x2d, labels)

3. Calcul du « Neighborhood Hit » (NH) [PNML08]. Pour chaque point, la métrique NH consiste à calculer, pour les k plus proches voisins (k-nn) de ce point, le taux des voisins qui sont de la même classe que le point considéré. La métrique NH est ensuite moyennée sur l’ensemble de la base. Le code suivant permet de calculer la métrique NH, en utilisant la classe NearestNeighbors du module sklearn.neighbors :

def neighboring_hit(points, labels):
  k = 6
  nbrs = NearestNeighbors(n_neighbors=k+1, algorithm='ball_tree').fit(points)
  distances, indices = nbrs.kneighbors(points)

  txs = 0.0
  txsc = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
  nppts = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

  for i in range(len(points)):
    tx = 0.0
    for j in range(1,k+1):
      if (labels[indices[i,j]]== labels[i]):
        tx += 1
    tx /= k
    txsc[labels[i]] += tx
    nppts[labels[i]] += 1
    txs += tx

  for i in range(10):
    txsc[i] /= nppts[i]

  return txs / len(points)

Question :

En quoi les trois métriques ci-dessus sont-elles liées au problème de la séparabilité des classes ? Qu’est-ce qui les diffère ?

Compléter le script exo4.py pour calculer les différentes métriques.

  • Vous pouvez ensuite utiliser la fonction visualization suivante pour afficher les points ainsi que leur labels, et de visualiser les trois métriques précédentes :

def visualization(points2D, labels, convex_hulls, ellipses ,projname, nh):

 points2D_c= []
  for i in range(10):
      points2D_c.append(points2D[labels==i, :])
  # Data Visualization
  cmap =cm.tab10

  plt.figure(figsize=(3.841, 7.195), dpi=100)
  plt.set_cmap(cmap)
  plt.subplots_adjust(hspace=0.4 )
  plt.subplot(311)
  plt.scatter(points2D[:,0], points2D[:,1], c=labels,  s=3,edgecolors='none', cmap=cmap, alpha=1.0)
  plt.colorbar(ticks=range(10))

  plt.title("2D "+projname+" - NH="+str(nh*100.0))

  vals = [ i/10.0 for i in range(10)]
  sp2 = plt.subplot(312)
  for i in range(10):
      ch = np.append(convex_hulls[i].vertices,convex_hulls[i].vertices[0])
      sp2.plot(points2D_c[i][ch, 0], points2D_c[i][ch, 1], '-',label='$%i$'%i, color=cmap(vals[i]))
  plt.colorbar(ticks=range(10))
  plt.title(projname+" Convex Hulls")

  def plot_results(X, Y_, means, covariances, index, title, color):
      splot = plt.subplot(3, 1, 3)
      for i, (mean, covar) in enumerate(zip(means, covariances)):
          v, w = linalg.eigh(covar)
          v = 2. * np.sqrt(2.) * np.sqrt(v)
          u = w[0] / linalg.norm(w[0])
          # as the DP will not use every component it has access to
          # unless it needs it, we shouldn't plot the redundant
          # components.
          if not np.any(Y_ == i):
              continue
          plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], .8, color=color, alpha = 0.2)

          # Plot an ellipse to show the Gaussian component
          angle = np.arctan(u[1] / u[0])
          angle = 180. * angle / np.pi  # convert to degrees
          ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
          ell.set_clip_box(splot.bbox)
          ell.set_alpha(0.6)
          splot.add_artist(ell)

      plt.title(title)
  plt.subplot(313)

  for i in range(10):
      plot_results(points2D[labels==i, :], ellipses[i].predict(points2D[labels==i, :]), ellipses[i].means_,
      ellipses[i].covariances_, 0,projname+" fitting ellipses", cmap(vals[i]))

  plt.savefig(projname+".png", dpi=100)
  plt.show()
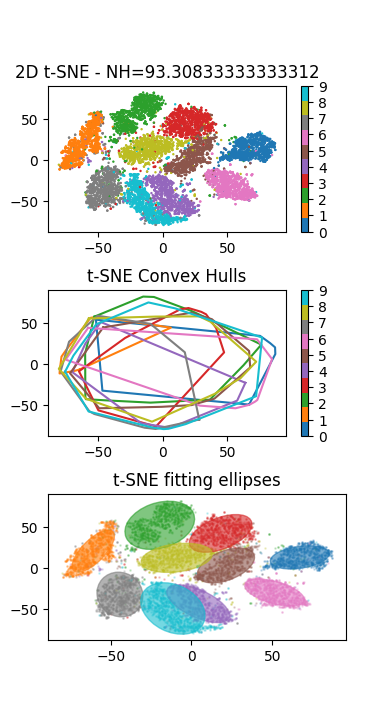
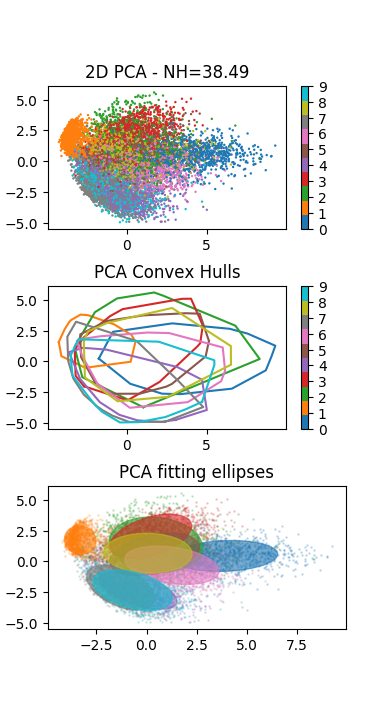
logo1 logo2

  • Analyser la distribution des points et des classes : que peut-on en conclure ?

Exercice 5 : Visualisation des représentations internes des réseaux de neurones

On va maintenant s’intéresser à visualisation de l’effet de « manifold untangling » permis par les réseaux de neurones.

Créer un script exo5.py dont l’objectif va être d’utiliser la méthode t-SNE de l’exercice 2 pour projeter les couches cachés des réseaux de neurones dans un espace de dimension 2, ce qui permettra de visualiser la distribution des représentations internes et des labels.

  • Commencer par charger le Perceptron entraîné avec Keras dans la partie précédente, en utilisant la méthode loadModel(savename) suivante:

from keras.models import model_from_yaml
def loadModel(savename):
  with open(savename+".yaml", "r") as yaml_file:
    model = model_from_yaml(yaml_file.read())
  print("Yaml Model ",savename,".yaml loaded ")
  model.load_weights(savename+".h5")
  print("Weights ",savename,".h5 loaded ")
  return model

  • On pourra vérifier l’architecture du modèle chargé avec la méthode summary().

  • On pourra également évaluer les performances du modèle chargé sur la base de test de MNIST pour vérifier son comportement. N.B : il faudra avoir compilé le modèle au préalable.

On veut maintenant extraire la couche cachée (donc un vecteur de dimension 100) pour chacune des images de la base de test.

  • Pour cela,on va utiliser la méthode model.pop() (permettant de supprimer la couche au sommet du modèle) deux fois (on supprime la couche d’activation softmax et la couche complètement connectée). Ensuite on peut appliquer la méthode model.predict(X_test) sur l’ensemble des données de test.

  • Finalement, on va utiliser la méthode t-SNE mise en place à l’exercice 2 pour visualiser les représentations internes des données.

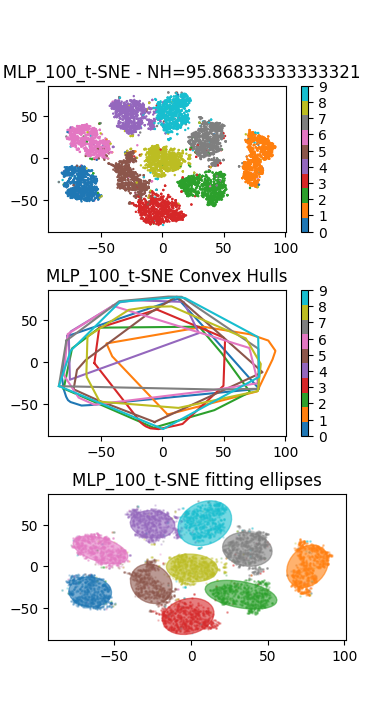
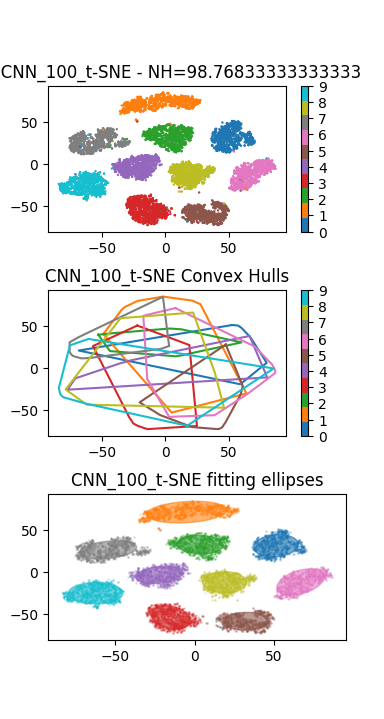
Conclure sur la capacité des réseaux de neurones à résoudre le problème du Manifold Untangling.

En plus du Perceptron précédent, on pourra visualiser les représentations internes apprises par un réseau convolutif de type LeNet de la partie précédente. Le résultat ci-dessous montre un résultat de visualisation obtenu avec un Perceptron (à gauche), et un réseau convolutif (à droite) :

logo3 logo4

Hot33

H. Hotelling. Analysis of a Complex of Statistical Variables Into Principal Components. Warwick & York, 1933. URL: https://books.google.fr/books?id=qJfXAAAAMAAJ.

LBD+89

Yann LeCun, Bernhard Boser, John S Denker, Donnie Henderson, Richard E Howard, Wayne Hubbard, and Lawrence D Jackel. Backpropagation applied to handwritten zip code recognition. Neural computation, 1(4):541–551, 1989.

PNML08

Fernando Vieira Paulovich, Luis Gustavo Nonato, Rosane Minghim, and Haim Levkowitz. Least square projection: A fast high-precision multidimensional projection technique and its application to document mapping. IEEE Trans. Vis. Comput. Graph., 14(3):564–575, 2008.

vdMH08

Laurens van der Maaten and Geoffrey E. Hinton. Visualizing high-dimensional data using t-sne. Journal of Machine Learning Research, 9:2579–2605, 2008.