TP 1 RL : Dynamic programing¶
Ce TP est disponible sur colab : ici et est téléchargeable ici
L’objectif de ce TP est de se familiariser avec la programmation dynamique pour le calcul de fonction de valeur d’état et de politique. Nous nous commencerons avec un environnement très simple : un griddworld de taille \(10\times 10\).
import numpy as np
from matplotlib import pyplot as plt
from time import sleep
from IPython.display import clear_output
import math
import numpy.matlib
import imageio
#@title Utils functions
def plot_pi(pi):
plt.xticks(np.arange(-1, N+1, 1))
plt.yticks(np.arange(-1, N+1, 1))
plt.grid( which='major')
param = {'lw':3,
'head_width':2/N}
for i in range(pi.shape[0]):
ll = pi[i,:]
x = i%N
y = N - math.ceil((i+1)/N)
args = np.argwhere(ll>0)
for n in args:
if n==0:
plt.arrow(x,y,.5,0,**param)
elif n==1:
plt.arrow(x,y,0,.5,**param)
elif n==2:
plt.arrow(x,y,-.5,0,**param)
elif n==3:
plt.arrow(x,y,0,-.5,**param)
def get_next_Vij(V_2d,i,j):
if i<0 or i>N or j<0 or j>N:
raise ValueError("indices must be between 0 and N")
if i==0:
if j==N-1:
ll = (-1e3,-1e3,V_2d[i,j-1],V_2d[i+1,j])
else:
ll = (V_2d[i,j+1],-1e3,V_2d[i,j-1],V_2d[i+1,j])
elif j==0:
if i==N-1:
ll = (V_2d[i,j+1],V_2d[i-1,j],-1e3,-1e3)
else:
ll = (V_2d[i,j+1],V_2d[i-1,j],-1e3,V_2d[i+1,j])
elif i==N-1:
ll = (V_2d[i,j+1],V_2d[i-1,j],V_2d[i,j-1],-1e3)
elif j==N-1:
ll = (-1e3,V_2d[i-1,j],V_2d[i,j-1],V_2d[i+1,j])
else:
ll = (V_2d[i,j+1],V_2d[i-1,j],V_2d[i,j-1],V_2d[i+1,j])
return ll
def get_Ppi(P,pi):
P = np.zeros([N**2,N**2])
p = 1
pi = np.array(pi)
if pi.size == 4:
pi = np.matlib.repmat(pi,N**2,1)
for i in range(N):
for j in range(N):
s = i*N+j
s_E = i*N+j+1
s_N = (i-1)*N+j
s_O = i*N+j-1
s_S = (i+1)*N+j
if j < N-1:
P[s,s_E] = p*pi[i*N+j,0]
else :
P[s,s] = p*pi[i*N+j,0]
if i > 0:
P[s,s_N] = p*pi[i*N+j,1]
else :
P[s,s] = p*pi[i*N+j,1]
if j > 0:
P[s,s_O] = p*pi[i*N+j,2]
else :
P[s,s] = p*pi[i*N+j,2]
if i < N-1:
P[s,s_S] = p*pi[i*N+j,3]
else :
P[s,s] = p*pi[i*N+j,3]
if (i,j)==(0,N-1):
P[s,s] = p*pi[i*N+j,0] + p*pi[i*N+j,1]
if (i,j)==(N-1,0):
P[s,s] = p*pi[i*N+j,2] + p*pi[i*N+j,3]
P[0,:] = 0
P[N**2-1,:]=0
return P
Partie 1 : Initialisation¶
Pour commencer nous allons définir la dynamique du modèle et en particulier la matrice de transition \(\mathcal P\) du griddworld ainsi que la matrice de récompense \(\mathcal R^\pi \in \mathbb R^{N,N}\) pour une politique de mouvement uniforme avec une probabilité \(\pi = 0.25\) constante et récompense constante poour chaque état \(r = -1\) sauf pour les états terminaux \((0,0)\) et \((N,N)\) où \(r=0\).
N = 10
R = -1*np.ones([N**2,1])
R[0] = 0
R[N**2-1] = 0
Création de la matrice de transition pour une politique de mouvements uniforme avec une probailité \(\pi\) = 0.25 et une transition déterministe \(p(s' | s, a) = 1\) pour \(s'\) situé en \(E,N,O\) ou \(S\) par rapport à \(s\).
coding task
Complétez l’mplémentation de la matrice \(\mathcal P\) associé à un
choix aléatoire parmis les 4 directions \(E,N,O\) ou \(S\).
Attention on part du principe que l’agent ne passe pas à travers les
bords et une tentative de sorti du griddworld ramène dans le même état
(d’où les if else imbriqués).
P = np.zeros([N**2,N**2])
p = 1
pi = .25
for i in range(N):
for j in range(N):
s = i*N+j
s_E = i*N+j+1
s_N = (i-1)*N+j
s_O = i*N+j-1
s_S = (i+1)*N+j
if j < N-1:
P[s,s_E] = # à compléter avec la bonne probabilité
else :
P[s,s] = # à compléter avec la bonne probabilité
if i > 0:
P[s,s_N] = # à compléter avec la bonne probabilité
else :
P[s,s] = # à compléter avec la bonne probabilité
if j > 0:
P[s,s_O] = # à compléter avec la bonne probabilité
else :
P[s,s] = # à compléter avec la bonne probabilité
if i < N-1:
P[s,s_S] = # à compléter avec la bonne probabilité
else :
P[s,s] = # à compléter avec la bonne probabilité
if (i,j)==(0,N-1) or (i,j)==(N-1,0):
P[s,s] = # à compléter avec la bonne probabilité
P[0,:] = 0
P[N**2-1,:]=0
plt.imshow(P)
<matplotlib.image.AxesImage at 0x7fd2285a7fd0>
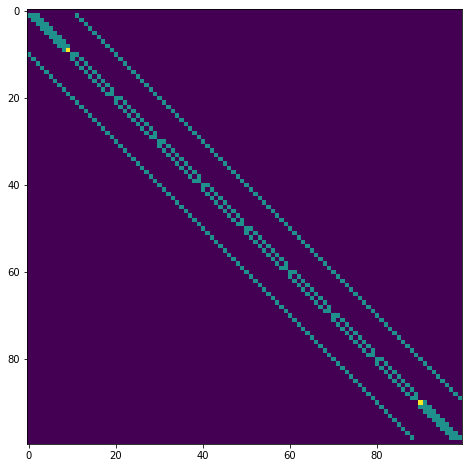
Partie 2 : Estimation de la politique et de la valeur des états associée¶
Coding Task: Compléter la fonction suivante permettant d’obtenir la fonction de valeur d’état en implémentant la récursion de Bellman.
def get_V(iter,P,R,gamma,show=1):
V = np.zeros([N**2,1])
for n in range(iter):
V = # Votre code ici
if show and n % 100 == 99:
clear_output()
plt.imshow(np.reshape(V,[N,N]))
plt.title(f'Iteration = {n+1}')
plt.show()
sleep(1)
return V
Maintenant que nous avons toutes nos fonctions, nous pouvons calculer la fonction de valeur d’état en itérant sur notre politique \(\pi\) :
V = np.zeros([N**2,1])
gamma = 1
n_iter = 500
fig = plt.figure()
V = get_V(n_iter,P,R,gamma)
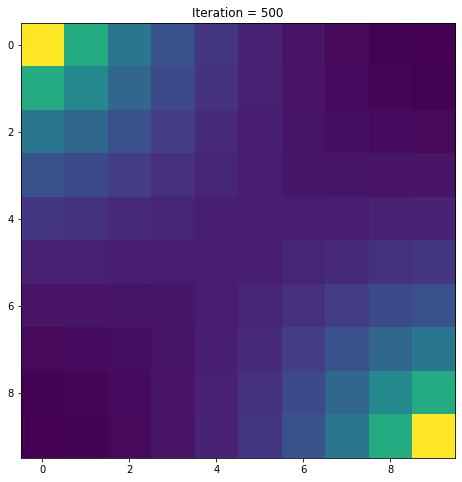
Sans surprise, plus on est proche des points à atteindre, plus la valeur des états est élevée.
Amélioration de la politique par action gloutonne : l’évaluation de la fonction de coût associée à notre politique naive nous permet de mettre en évidence une politique \(\pi' \geq \pi\). Pour cela il nous faut calculer en tout point quel est le meilleur coup à jouer, c’est à dire la poltique gloutonne ou \(greedy\).
coding task: Compléter la fonction suivante pour obtenir la greedy policy à partic de la fonction de valeur d’état. La fonction get_next_Vij() renvoie la valeur des états voisins dans un tableau de taille le nombre d’action (donc 4 dans notre cas) avec l’espérance de la valeur d’état après avoir choisi l’action correspondant à l’indice du tableau.
def greedy_policy(V):
V_2d = np.reshape(V,[N,N])
pi = np.zeros([N**2,4])
for i in range(N):
for j in range(N):
if i==0 and j==0 or i==N-1 and j==N-1:
continue
V_voisin = get_next_Vij(V_2d,i,j)
# Votre code ici
pi[i*N+j,args] = ...
return pi
Nous pouvons enfin afficher la valeur de la politique pour ce griddworld
pi = greedy_policy(V)
plot_pi(pi)
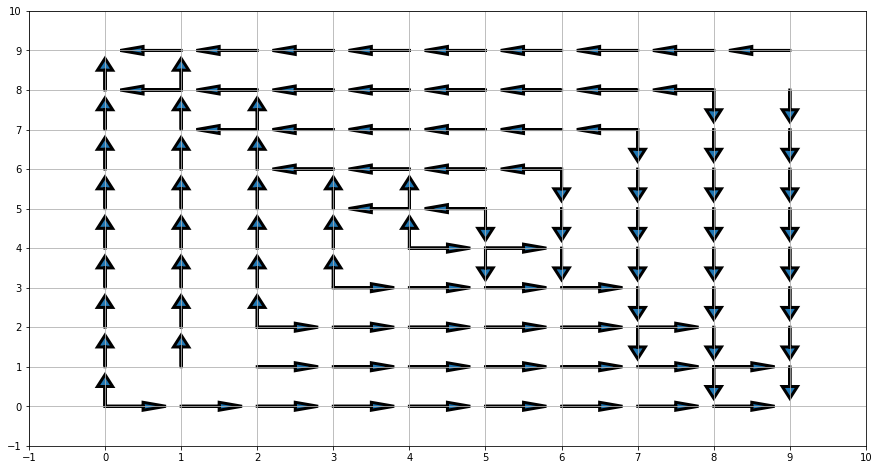
Partie 3 : Maximisation de la politique¶
Dans le cas précédent, tout l’espace était exploré, conduisant à découvrir la politique optimale après une seule itération. A présent, nous allons initialiser notre politique en faisant le choix d’aller toujours à l’est puis améliorer la politique de façon gloutonne une fois la fonction de valeur estimée.
coding task : compléter le code suivant pour permettre d’alterner entre calcul de la fonction de valeur d’état et optimisation de la politique de façon à converger vers la politique idéale.
iter_total = 10
iter_policy = 100
show = 1
show_every = 1
gamma = .5
plt.rcParams['figure.figsize'] = [15, 8]
P_pi = get_Ppi([1,0,0,0],P)
for i in range(iter_total):
# Votre code ici
V = ...
pi = ...
P_pi = ...
if show and i % show_every == 0:
clear_output()
plt.subplot(121)
plt.imshow(np.reshape(V,[N,N]), aspect="auto")
axs[0].set_title('Value Function')
plt.subplot(122)
plot_pi(pi)
axs[1].set_title('Next policy')
plt.show()
sleep(1)

Partie 4 : Labyrinthe¶
A présent évaluons la valeur des différents états ainsi que la politique optimale pour un labyrinthe. Le labyrinthe est donné par la matrice suivante :
maze = np.array([[0,0,1,1,1,1,1,1,1,1,1],
[1,0,1,0,1,0,0,0,0,0,1],
[1,0,1,0,1,1,1,0,1,0,1],
[1,0,0,0,0,0,1,0,1,0,1],
[1,0,1,1,1,0,1,0,1,1,1],
[1,0,1,0,1,0,1,0,1,0,0],
[1,1,1,0,1,0,1,0,1,0,1],
[0,0,0,0,0,0,0,0,0,0,1],
[1,1,1,1,1,0,1,1,1,1,1],
[1,0,0,0,0,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1,0,0]])
plt.imshow(maze)
<matplotlib.image.AxesImage at 0x7fd228b3c310>

À vous de jouer !
À vous de réécrire les matrices de transition et de récompense pour ce nouveau problème.
