Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.
Cours - SVM linéaires¶
« Statistics is the grammar of science. »
(Karl Pearson)
Objectif¶
Dans cette séance nous examinerons les machines à vecteurs de support dans leur version linéaire (en anglais Support Vector Machines ou SVM), et dans les séances à suivre les SVM non-linéaires et les autres algorithmes à noyaux.
On donne un ensemble d’apprentissage \(\{(x_i, y_i)\}_{i=1,...,n}\) où \(x_i\in \mathcal{X}\) (souvent \(\mathcal{X} = \mathbb{R}^d\)) et \(y_i\in\{-1, +1\}\). Dans un problème de classification à deux classes, le but est (en utilisant les données d’apprentissage \(\{(x_i, y_i)\}_{i=1,...,n}\) bien sûr) de chercher une fonction \(f:\mathcal{X} \rightarrow \mathbb{R}\) qui permet de prédire si un nouvel exemple \(x\in \mathcal{X}\) appartient à la classe −1 ou à la classe +1.
Le principe est de séparer l’espace de descripteurs \(\mathcal{X}\) en deux parties : \(\mathcal{X} = \{x \in \mathcal{X} | f(x) > 0\} \cup \{x \in \mathcal{X} | f(x) < 0\}\). Si \(f(x) > 0\) alors \(x\) est affecté à la classe +1, si \(f(x) < 0\) alors \(x\) est affecté à la classe -1, et si \(f(x) = 0\) alors \(x\) se trouve sur la « surface de séparation » entre les deux classes et le classifieurs ne peut pas l’affecter à l’une des classes.
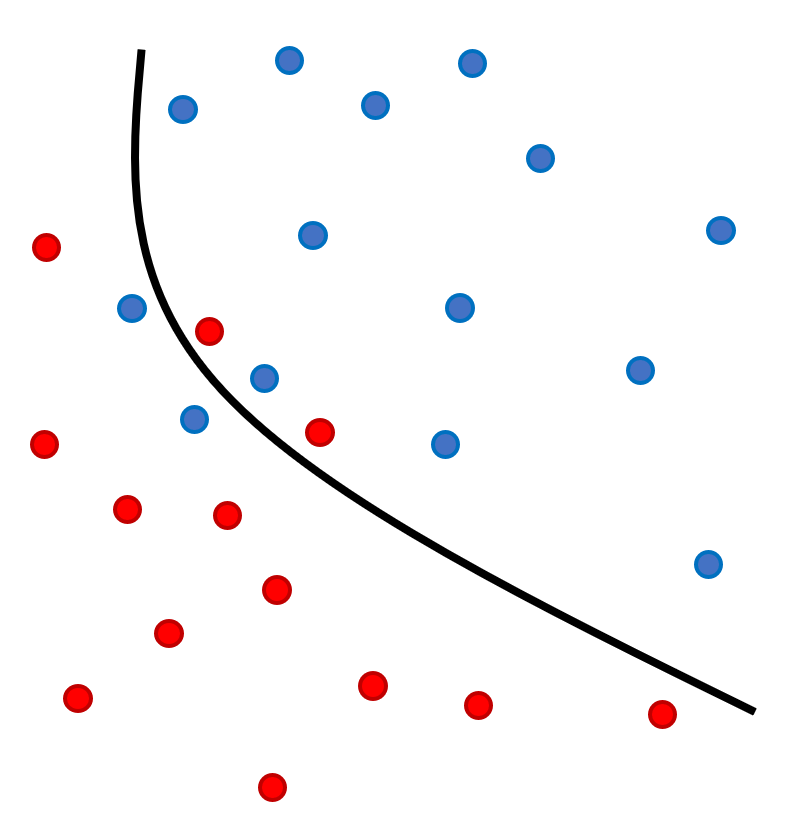
Fig. 43 Problème de séparation à deux classes : trouver la fonction \(f\) tel que \(f(x) = 0\) sépare les deux classes avec le moins d’erreurs possible.¶
Séparateurs à vaste marge¶
Pour un problème de classification linéaire on suppose que les deux classes (-1 et +1) sont séparables par un hyperplan. On considère \(\mathcal{X} = \mathbb{R}^d\) et donc un vecteur \(x\) a \(d\) composantes numériques \(x = (x_1, \dots, x_d)\). Un hyperplan \(f(x)\) a donc la forme suivante :
où \(w\) est le vecteur orthogonal à l’hyperplan et \(b\) est le déplacement par rapport à l’origine. \(\langle \cdot, \cdot \rangle\) est le produi scalaire usuel en \(\mathcal{X} = \mathbb{R}^d\) : \(\langle x, y \rangle = \sum_{i=1}^d x_i y_i\).
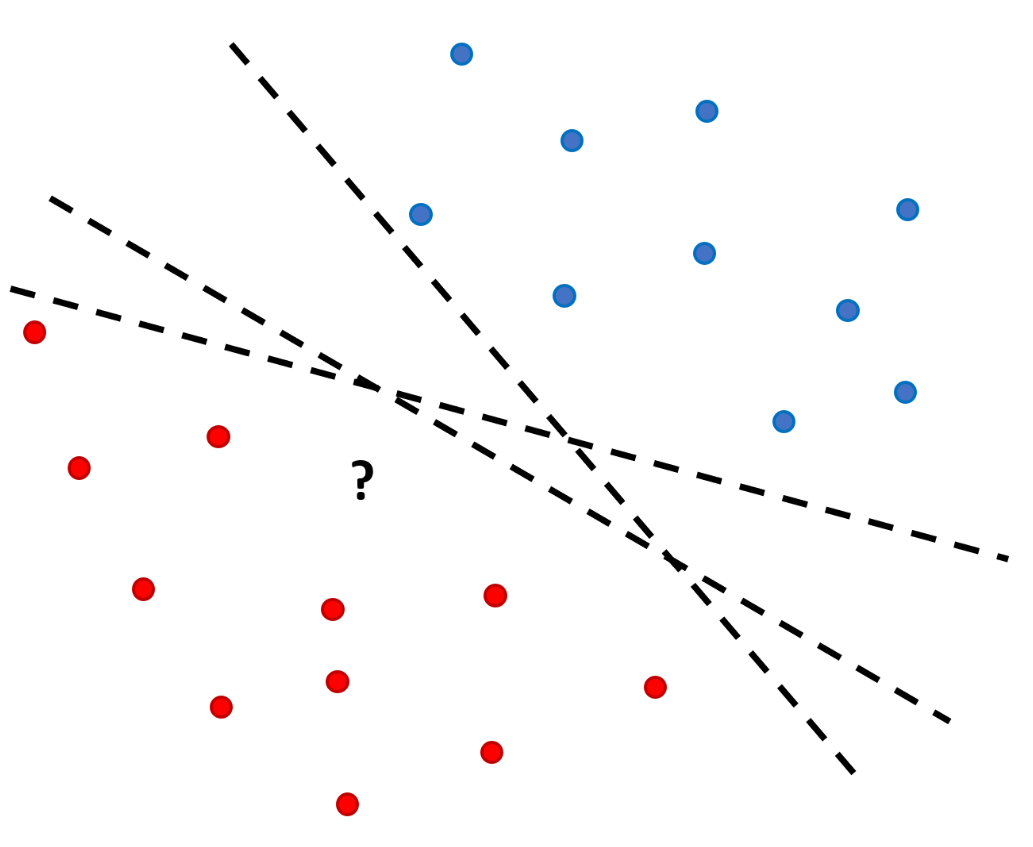
Fig. 44 Problème de séparation linéaire à deux classes : quel est le meilleur hyperplan parmi tous ceux qui séparent les données ?¶
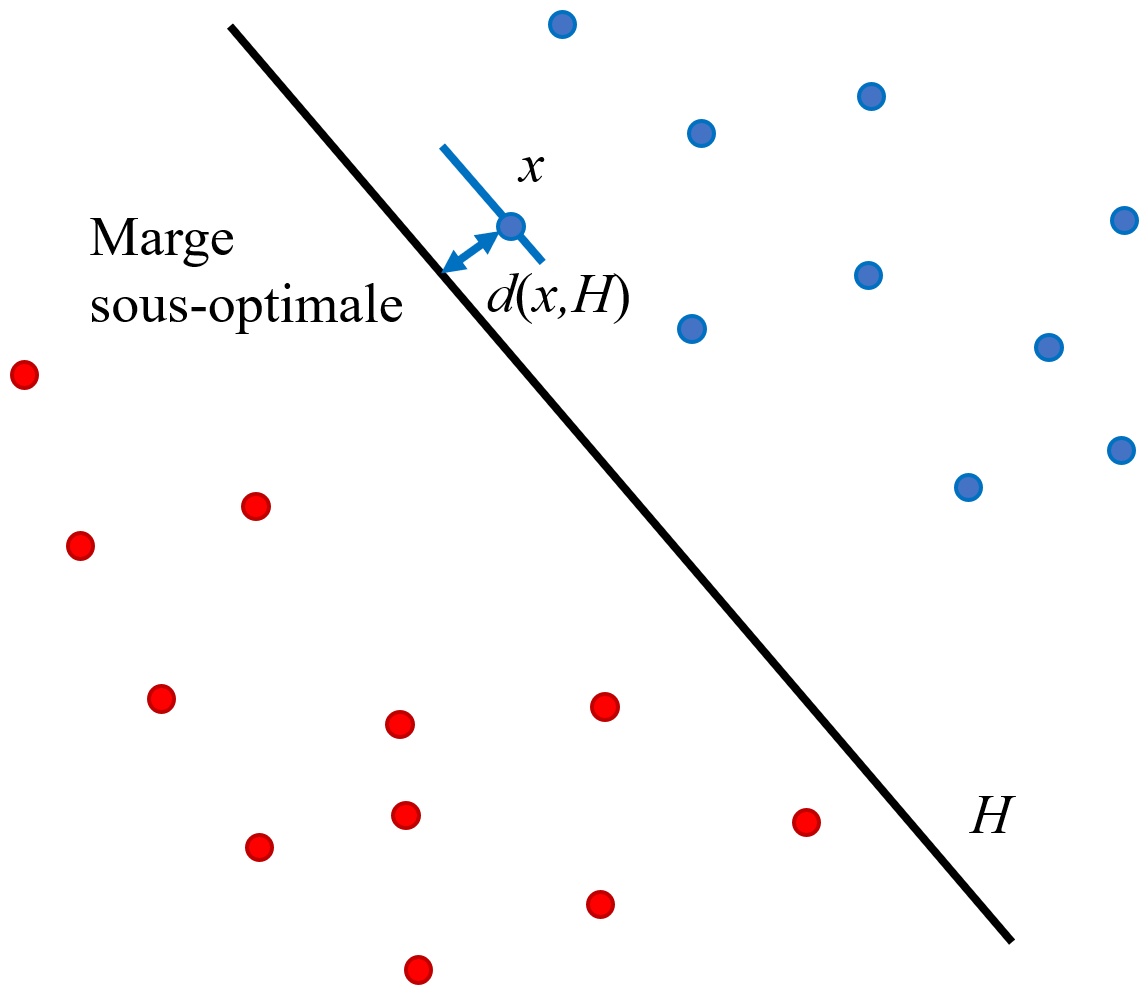
Pour juger la qualité d’un hyperplan en tant que séparateur on utilise la distance entre les exemples d’apprentissage et ce séparateur. Plus précisément, la « marge » d’un problème d’apprentissage est définie comme la distance entre le plus proche exemple d’apprentissage et l’hyperplan de séparation. Pour un hyperplan \(H\) on a :
Les SVM linéaires cherchent le séparateur (l’hyperplan de séparation) qui maximise la marge. On appelle cela « séparateur à vaste marge ».
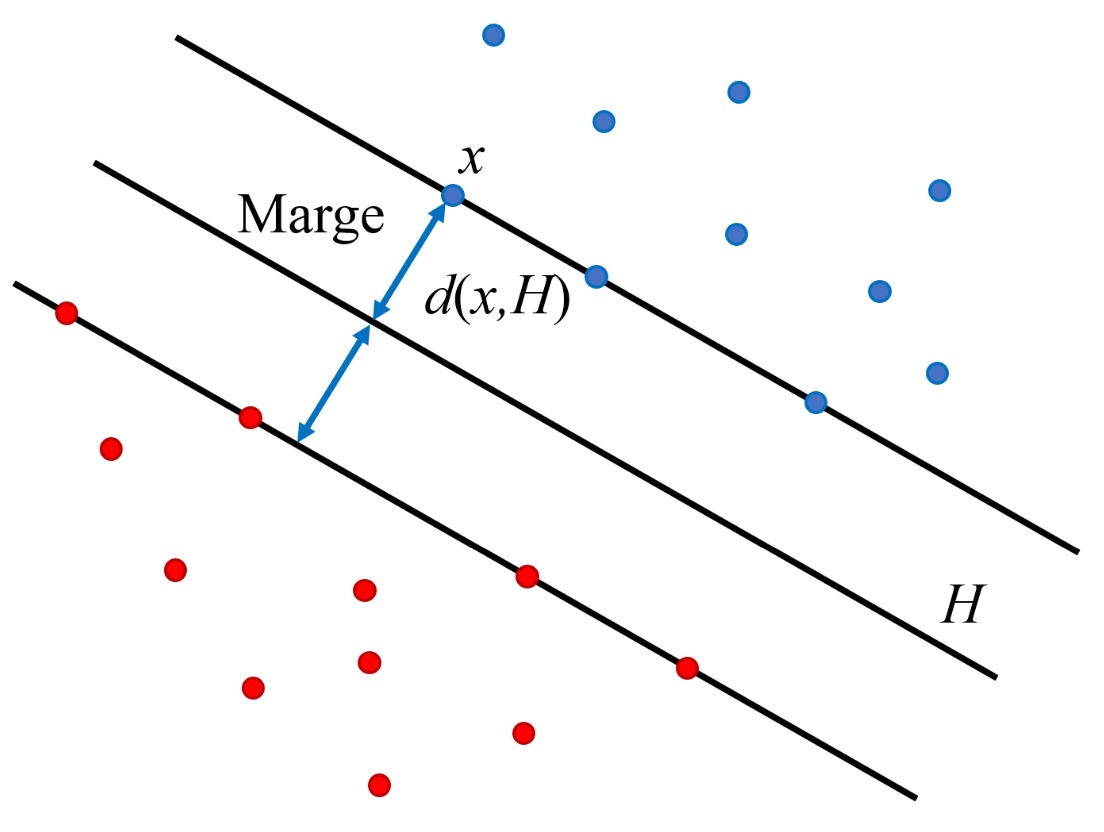
Fig. 45 Le séparateur idéal correspond intuitivement à l’hyperplan qui passe « au milieu » entre les données sans préférence pour une classe ou une autre. C’est le séparateur de marge maximale.¶
Les éléments de la classe 1 les plus proches de ce séparateur se trouvent à la même distance du séparateur que les éléments les plus proches de la classe 2 (cette distance est égale à la marge). Ces éléments, soit d’une classe soit de l’autre, s’appellent « vecteurs de support ».
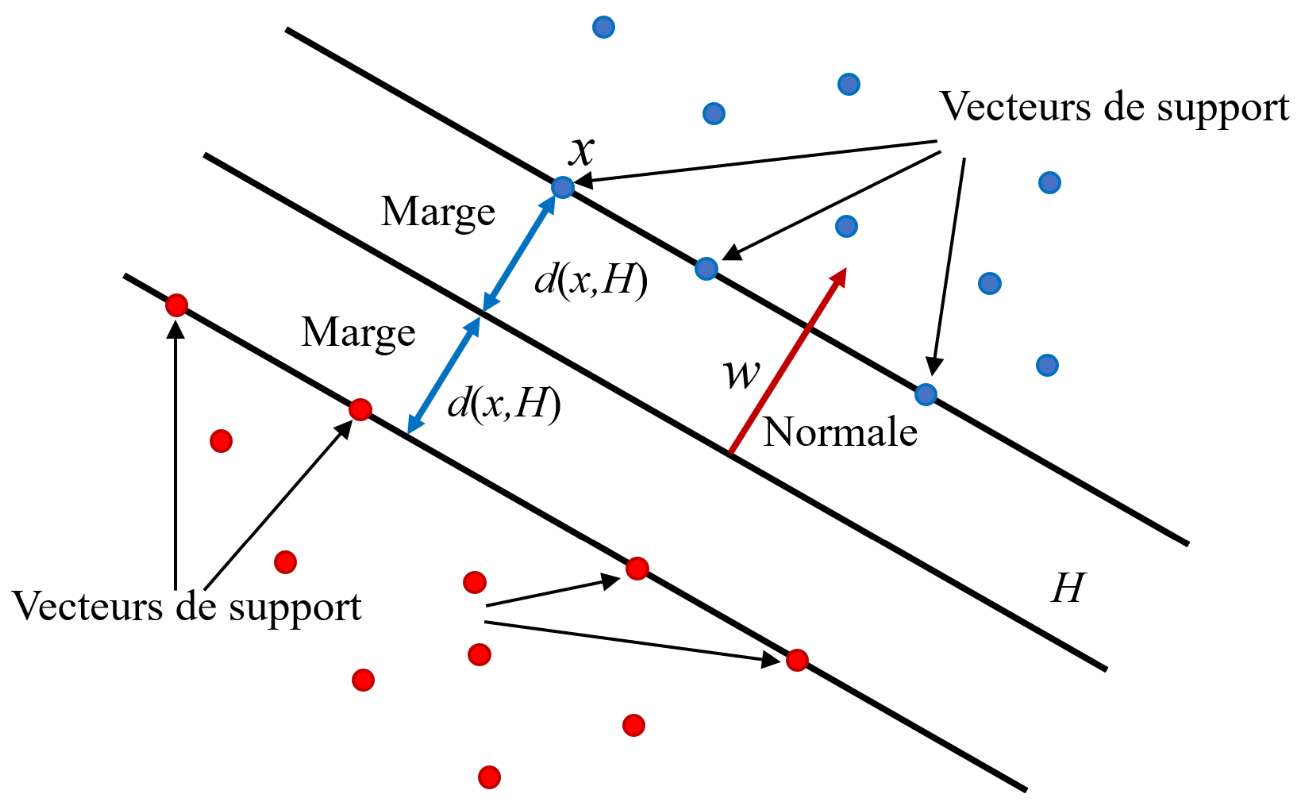
Fig. 46 Les « vecteurs de support » se trouvent a une distance égale à la marge d’un côte ou de l’autre de l’hyperplan de séparation¶
Intuitivement, ce sont les vecteurs de support qui déterminent le séparateur, par l’intermédiaire de la fonction distance et de leur configuration géométrique.
Une fois le séparateur \(f(x)\) trouvé, la classification d’un nouvel exemple se fait par une simple décision à seuil zéro :
\(f(x) = 0\) : l’élément se trouve sur la frontière de séparation, pas de décision.
\(f(x) > 0\) : classe 1.
\(f(x) < 0\) : classe 0.
SVM linéaire (cas séparable)¶
On suppose d’abord que les données d’apprentissage sont linéairement séparables, c’est à dire qu’il existe un hyperplan qui sépare les données sans erreur. Dans ce cas, on cherche l’hyperplan de marge maximale :
Si \(x_s\) est un vecteur de support et \(H = \{x|w^\top x+b=0\}\), alors la marge est donnée par :
En fait cette quantité est deux fois la marge (par rapport à la définition donnée en haut). On utilise cette quantité pour des raisons de simplicité de l’écriture des équations plus tard, mais ceci ne change en rien le problème d’optimisation (maximiser la marge ou deux fois la marge conduit à la même solution).
Les paramètres \(w\) et \(b\) ne sont pas uniques, \(kw\) et \(kb\) donnent la même surface de séparation :
On impose alors la condition de normalisation \(|w^\top x_s + b| = 1\) pour les vecteurs de support \(x_s\), ce qui conduit à :
On arrive donc au problème d’optimisation suivant (appelé problème primal) :
Rappelons la condition de normalisation : \(w\cdot x_i + b = 1\) si \(x_i\) est un vecteur de support de la classe +1 et \(w\cdot x_i + b = -1\) si \(x_i\) est un vecteur de support de la classe -1. Dans ce cas, comme le problème est séparable, il n’y a pas d’exemple d’apprentissage entre les deux hyperplans, \(w\cdot x_i + b = 1\) et \(w\cdot x_i + b = -1\) (on dit par abus de langage « dans la marge »). Nous obtenons :
Si \(y_i = 1\) alors \(w\cdot x_i + b \geq 1\) et donc \(y_i(w\cdot x_i + b) \geq 1\),
Si \(y_i = -1\) alors \(w\cdot x_i + b \leq -1\) et donc \(y_i(w\cdot x_i + b) \geq 1\),
ce qui explique les conditions présentes dans le problème d’optimisation.
La résolution de ce problème peut se faire directement par des méthodes stochastique de type Gauss-Seidel, algorithmes de point intérieur, de type Newton ou de type gradient conjugué.
Il est toutefois mieux de passer à la formulation duale de ce problème :
Le dual est un problème quadratique de taille \(n\) (égal au nombre d’observations).
Pour ce type de problème (optimisation quadratique) il existe des algorithmes bien étudiés et très performants.
La formulation duale fait apparaître la matrice de Gram \(XX^T\), ce qui permet de gérer le cas non linéaire à travers des algorithmes à noyaux (qui seront étudiés dans la séance suivante).
Pour obtenir la formulation duale, on introduit les multiplicateurs \(\alpha_i\) de Lagrange (voir la méthode des multiplicateurs de Lagrange). Le lagrangien est donné par :
Le lagrangien doit être optimisé par rapport à \(w\), \(b\) et les multiplicateurs \(\alpha\). En annulant les dérivées partielles du lagrangien par rapport à \(w\) et \(b\), on obtient les relations :
Par substitution dans l’équation du lagrangien en haut on obtient le problème dual :
La solution du problème dual donne les multiplicateurs de Lagrange optimaux \(\alpha_i\). A partir des \(\alpha_i\) on obtient \(w\) par les relations en haut. Le paramètre \(b\) est obtenu à partir de la relation \(|x_s^T w + b| = 1\) valable pour tous les vecteurs de support \(x_s\).
Observation : les vecteurs de support sont ceux pour lesquels \(\alpha_i > 0\). En général leur nombre est beaucoup plus petit que le nombre total d’éléments dans la base d’apprentissage. Ajouter des échantillons qui ne sont pas des vecteurs supports à l’ensemble d’apprentissage n’a aucune influence sur la solution finale, c’est à dire seulement les vecteurs de support interviennent dans la fonction de décision (l’expression de la surface séparatrice entre les deux classes). Cette fonction de décision permettant de classer une nouvelle observation \(x\) est donnée par :
L’hyperplan solution ne dépend que du produit scalaire entre le vecteur d’entrée et les vecteurs de support. Cette particularité permet l’utilisation de fonctions noyau pour aborder des problèmes non linéaires (traités dans la séance de cours suivante).
Données non séparables linéairement¶
Souvent il arrive que même si le problème est linéaire, les données sont affectées par un bruit (par ex. bruit de capteur) et les deux classes se retrouvent mélangées autour de l’hyperplan de séparation. Pour gérer ce type de problème on utilise une technique dite de marge souple, qui tolère les mauvais classements :
Rajouter des variables de relâchement des contraintes \(\xi_i\),
Pénaliser ces relâchements dans la fonction objectif.
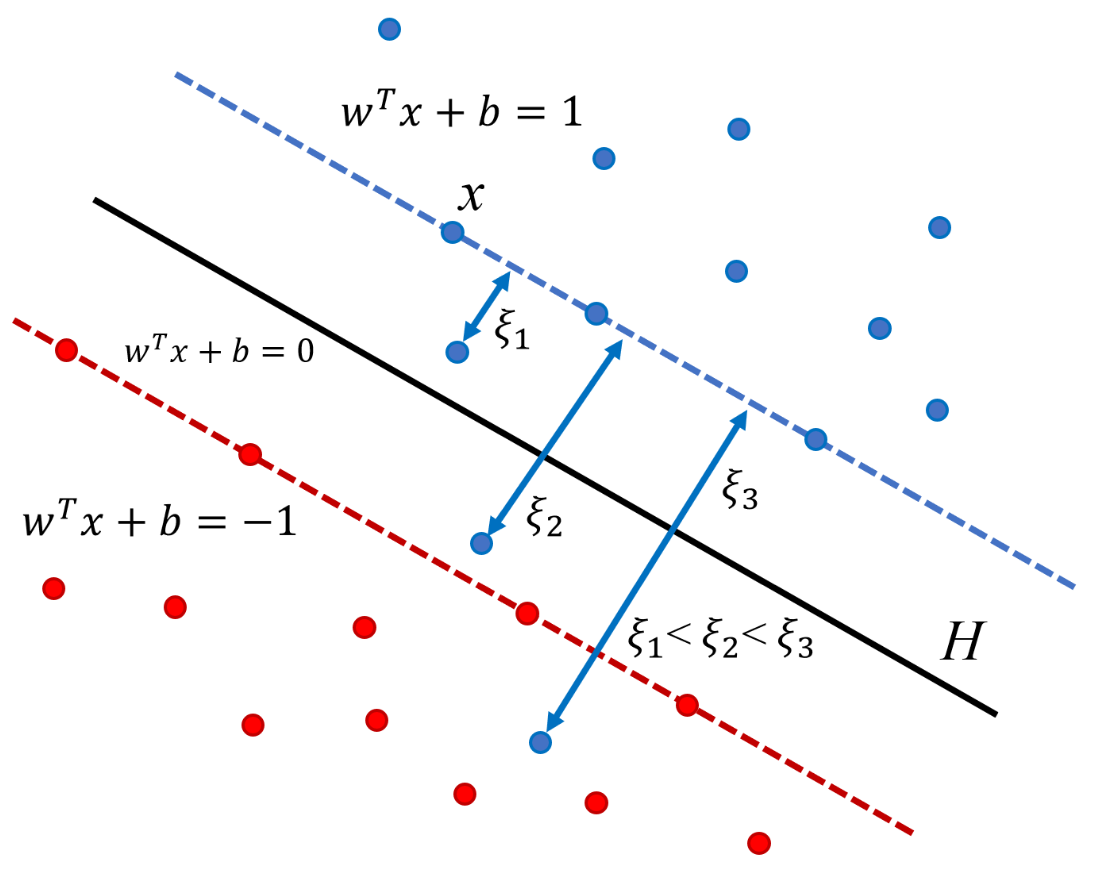
Fig. 47 Plus en exemple est éloigné du mauvais coté du séparateur (point bleu), plus la variable de relâchement \(\xi_i\) a une valeur importante.¶
L’intuition est de modéliser les erreurs potentielles par des variables d’écart positives \(\xi_i\) associées aux observations \((x_i, y_i), i = 1, \dots n\).
Si un point \((x_i, y_i)\) vérifie la contrainte de marge \(y_i (w^T x_i + b) \geq 1\) alors la variable d’écart (qui est une mesure du coût de l’erreur) est nulle.
Nous avons donc deux situations :
Pas d’erreur : \(y_i(w^T x_i + b) \geq 1 \Longrightarrow \xi_i = 0\),
Erreur : \(y_i(w^T x_i + b) < 1 \Longrightarrow \xi_i = 1 - y_i(w^T x_i + b) > 0\).
On associe à cette définition une fonction coût appelée « coût charnière » :
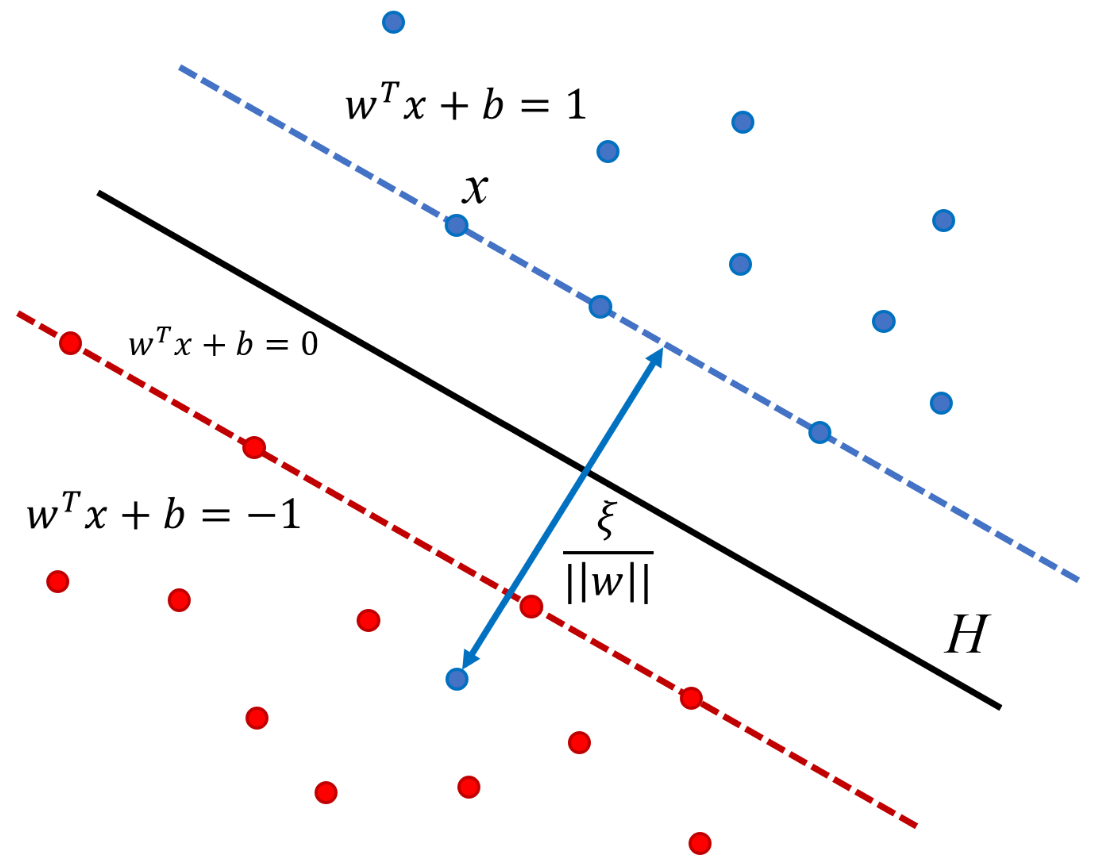
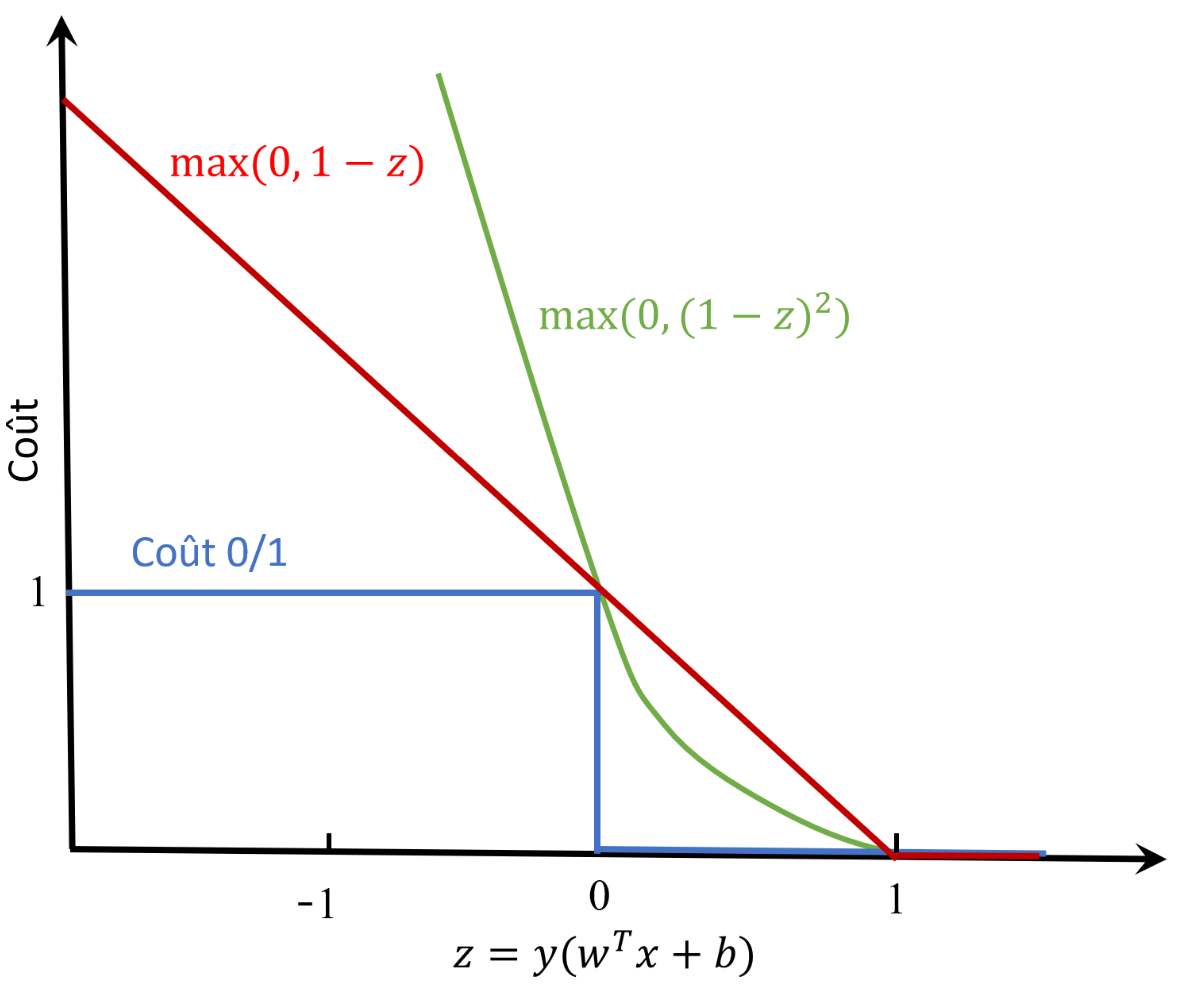
Figure en haut, à gauche : un seul point est mal classé (point bleu). L’écart mesure la distance du point à la marge numérique de l’hyperplan séparateur. A droite on montre plusieurs coûts possibles : coût 0/1, coût charnière et coût quadratique.
Le problème d’optimisation dans le cas des données non-séparables est donc :
Si toutes les variables d’écart \(\xi_i = 0\), on retrouve le problème linéairement séparable traité plus tôt.
Puisqu’il faut minimiser les deux termes simultanément, on introduit une variable d’équilibrage \(C > 0\) qui permet d’avoir une seule fonction objectif dans le problème d’optimisation :
\[\underset{w,b}{\min} \frac{1}{2}||w||^2 + C \sum_{i=1}^n\xi_i\]ce qui conduit à :
\[\begin{split}\left\{ \begin{array}{lll} \underset{w,b}{\min} \frac{1}{2}||w||^2 + C \sum_{i=1}^n\xi_i\\ \textrm{t.q.}\\ y_i(w\cdot x_i + b) \geq 1 - \xi_i, i = 1, \dots, n\\ \xi_i \geq 0, i = 1, \dots, n \end{array} \right.\end{split}\]
\(C\) est une variable de pénalisation des points mal classés faisant un compromis entre la largeur de la marge et les points mal classés. Les variables \(\xi_i\) s’appellent aussi variables ressort (anglais: slack variables).
Par la même procédure qu’avant, on obtient le problème dual :
Observations :
\(C\) joue le rôle d’une constante de régularisation (la régularisation est d’autant plus forte que \(C\) est proche de 0).
La différence pour le problème dual entre le cas séparable et non séparable est que les valeurs des \(\alpha_i\) sont majorées par \(C\).
Les points mal classés ou placés dans la marge ont un \(\alpha_i = C\).
\(b\) est calculé de sorte que \(y_i f(x_i) =1\) pour les points tels que \(C > \alpha_i > 0\).
La fonction de décision permettant de classer une nouvelle observation \(x\) est toujours
Pratiquement tous les environnements importants de modélisation mathématique (R, Matlab, Mathematica, Scipy, Scikit-learn, etc.) possèdent des implémentations performantes pour les SVM et méthodes à noyaux :
Scikit-Learn, http://scikit-learn.org/
Exemples SVM Toy¶
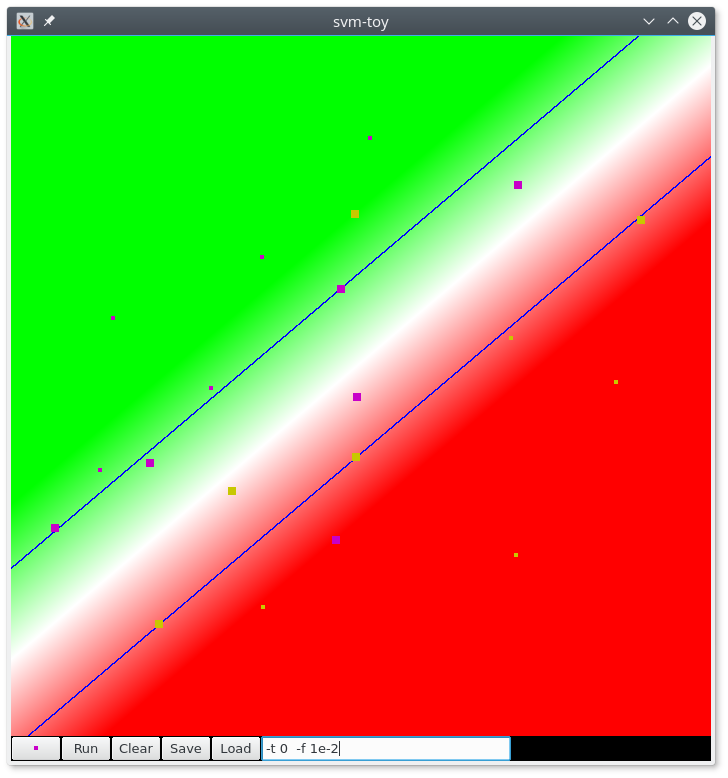
Fig. 48 Séparation linéaire avec LibSVM. Figure obtenue avec l’outil SVMToy (vecteurs de support en gras). Le blanc correspond à une valeur égale à zéro de la fonction de décision.¶
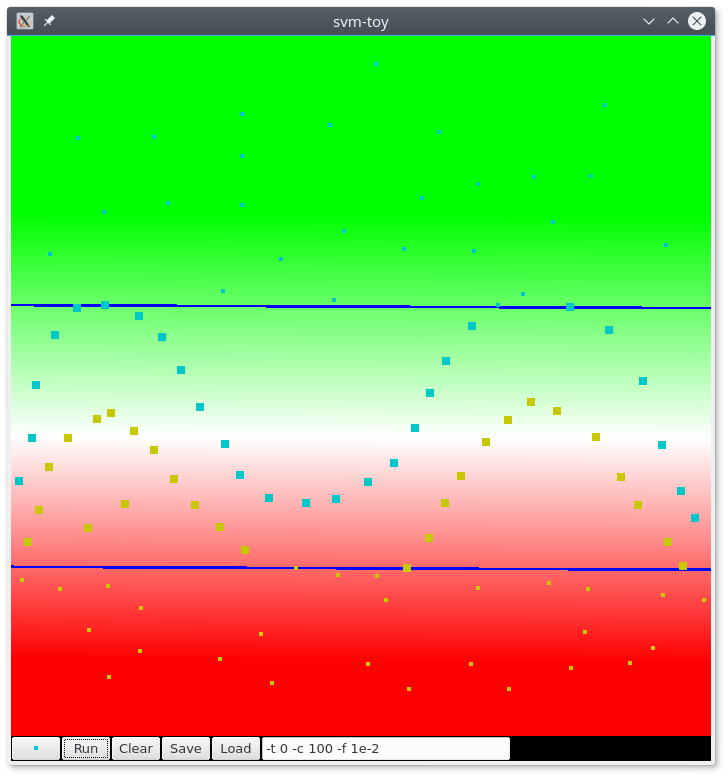
Fig. 49 Séparation linéaire avec LibSVM pour un problème non linéaire. Figure obtenue avec l’outil SVMToy (vecteurs de support en gras). Le blanc correspond à une valeur égale à zéro de la fonction de décision.¶
Références, livres, articles, web¶
- CM12
Cornuéjols, Miclet, Apprentissage artificiel : concepts et algorithmes, Eyrolles, 2012.
- SC08
Steinwart, Christmann, Support Vector Machines, Springer 2008.
- SS01
Scholkopf, Smola, Learning with Kernels, The MIT Press, 2001.
- HTF06
Hastie, Tibshirani, Friedman, The elements of statistical learning: data mining, inference, and prediction, New York, Springer Verlag, 2006.
- WikiStat
Machines à vecteurs supports (WikiStat), http://wikistat.fr
