Les informations pratiques concernant le déroulement de l’unité d’enseignement RCP209 « Apprentissage, réseaux de neurones et modèles graphiques » au Cnam se trouvent dans ce préambule.
Cours - Forêts Aléatoires¶
« Statistics is the grammar of science. »
(Karl Pearson)
Dans cette séance nous examinons plusieurs stratégies pour construire (ou assembler) des classifieurs performants à partir de classifieurs de base plus modestes. Ce sont les « méthodes d’agrégation ». Nous allons commencer par une discussion des avantages et des défauts des arbres de décision, surtout le problème des estimateurs de variance élevée. Ensuite nous présenterons les deux approches classiques conçues pour répondre à ce problème : le « Bagging » et les « Forêts aléatoires » et nous finirons par une courte introduction au Boosting, qui permet de combiner la sortie de plusieurs classifieurs simples pour en obtenir un meilleur résultat.
Estimateurs de variance élevée¶
Avantages des arbres de décision¶
Les arbres de décision ont un nombre de propriétés qui font d’eux un outil précieux, surtout quand il s’agit de faire l’analyse rapide d’un jeu de données ou d’élaborer un prototype de classifieur :
Modèle white box : le résultat est facile à conceptualiser, à visualiser et a interpréter.
Ils nécessitent peu de préparation de données (e.g. normalisation, etc.).
Le coût d’utilisation des arbres est logarithmique (classification d’une nouvelle donnée très rapide).
Ils sont capables d’utiliser des données catégorielles et continues.
Ils sont capables de gérer des problèmes multi-classes.
Ils ont un bon comportement par rapport aux valeurs extrêmes (outliers).
Ils gèrent bien les données manquantes.
Défauts des arbres de décision¶
Parfois les arbres générés ne sont pas équilibrés (ce qui implique que le temps de parcours n’est plus logarithmique). Il est donc recommandé d’équilibrer la base de données avant la construction, pour éviter qu’une classe domine (en termes de nombre d’exemples d’apprentissage).
Sur-apprentissage : parfois les arbres générés sont trop complexes et généralisent mal (solution : élagage, le contrôle de la profondeur de l’arbre et de la taille des feuilles).
Ils sont instables : des changements légers dans les données produisent des arbres très différents. Les changements des nœuds proches de la racine affectent beaucoup l’arbre résultant. On dit que les arbres produisent des estimateurs de variance élevée.
Le besoin de répondre à ce troisième problème, qui n’admet pas de solution par optimisation algorithmique, a conduit aux approches de type Bagging et « Forêts aléatoires ».
L’idée derrière et celle de la Réduction de variance : on utilise pour cela la moyenne de plusieurs estimateurs, calculés sur des données légèrement différentes, en somme utiliser le hasard pour améliorer les performances des algorithmes de base (qui sont les arbres de décision CART ici).
Ces améliorations ont été proposées par Breiman et al. dans [Bre96], [Bre01] et ont été beaucoup explorées depuis.
Bagging¶
Nous commençons par le Bagging (Bootstrap Agregating). Soit la base d’apprentissage décrite comme suit :
Les données sont décrites par les attributs : \(A_1, ..., A_p\), classe : \(C\),
Données d’apprentissage : \((x_i, y_i), x_i\in \mathbb{R}^p, y_i\in \mathbb{R}, i=1,...,N\),
\(y_i\) peuvent être des valeurs continues ou discrètes (étiquettes des classes),
\(x_i = (a_1^{(i)}, ..., a_p^{(i)})\).
On considère \(G(x)\) un modèle de prédiction appris sur un échantillon de données \(z = \{(x_i, y_i)\}_{i=1}^n\) (e.g. arbre de décision CART).
Algorithme bagging :
On tire au hasard dans la base d’apprentissage \(B\) échantillons avec remise \(z_i, i = 1, \dots, B\) (chaque échantillon ayant \(n\) points) — appelés échantillons bootstrap ;
Pour chaque échantillon \(i\) on calcule le modèle \(G_i(x)\) ;
Régression : agrégation par la moyenne \(G(x) = \frac{1}{B}\sum_{i=1}^BG_i(x)\) ;
Classement : agrégation par vote \(G(x) = \mathrm{Vote\,majoritaire\,}(G_1(x), \dots, G_B(x))\).
C’est l’estimateur moyenne qui aide a réduire la variance :
\(X_1, X_2, \dots, X_n\) variables aléatoires i.i.d. de moyenne \(\mu\) et variance \(\sigma^2\),
La moyenne \(\frac{1}{n}(X_1 + X_2 + \dots + X_n)\) est de variance \(\sigma^2/n\).
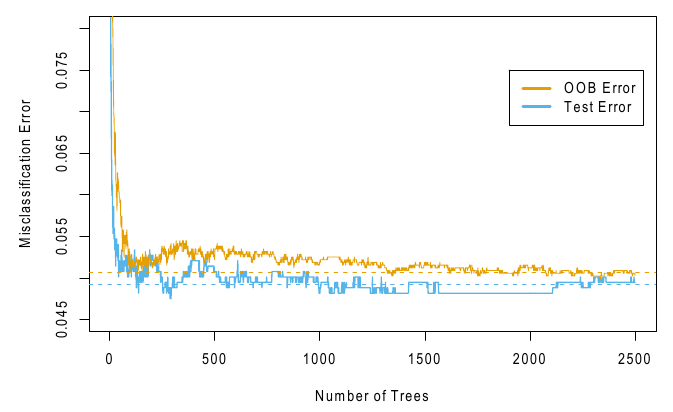
Le critère de performance pour le calcul de \(B\) est l’erreur OOB (Out Of Bag) :
Au lieu de faire un découpage classique test/validation de la base d’apprentissage, pour chaque échantillon \(x_k\) on construit un prédicteur (de type forêt aléatoire) en utilisant seulement les arbres \(G_i\) tel que \(x_i \notin z_i\) (donc \(x_i\) ne fait pas partie de l’échantillon de bootstrap de \(G_i\)).
Agrégation des erreurs OOB obtenues pour chaque échantillon (par la moyenne par exemple)
On choisit \(B\) ou l’erreur se stabilise et ne descend plus.
On peut montrer que, si \(B\) est grand, l’erreur OOB est presque identique à celle obtenue par validation croisée de type un contre tous (\(N\)-Fold où \(N\) est le nombre d’échantillons) : quand \(B \rightarrow \infty\) l’erreur OOB converge vers l’erreur N-fold [HTF09] (Chap. 15).
L’erreur OOB permet de tester l’éfficacité du modèle résultat pendant sa construction : quand l’erreur OOB se stabilise (ne descend plus) on peut arrêter le processus d’apprentissage.
Les défauts du bagging :
Les estimateurs \(G_i\) ne sont pas en réalité indépendants. En effet, \(G_i\) sont calculés sur des échantillons qui se recouvrent fortement (tirage avec remise) et donc ils sont corrélés.
Si \(X_1, X_2, \dots, X_B\) sont issus de variables aléatoires identiquement distribuées (mais pas indépendantes) de moyenne \(\mu\), variance \(\sigma^2\) et corrélation \(\rho = Corr(X_i, X_j), \forall i\neq j\), alors \(Y = \frac{1}{B}(X_1 + X_2 + \dots + X_B)\) est de variance
\[Var(Y) = \rho \sigma^2 + \frac{1-\rho}{B} \sigma^2\]
Quand \(B\) est grand le 2ème terme est négligeable mais le 1er non.
L’amélioration proposée par les forêts aléatoires est de baisser la corrélation entre les \(G_i\) à l’aide d’une étape supplémentaire de randomisation.
Forêts aléatoires¶
Les forêts aléatoires sont donc une amélioration du bagging pour les arbres de décision CART dans le but de rendre les arbres utilisés plus indépendants (moins corrélés).
Caractéristiques :
Elles donnent de bons résultats surtout en grande dimension,
Elles sont très simples à mettre en œuvre,
Elles ont peu de paramètres.
Algorithme « forêts aléatoires » [Bre01] :
On tire au hasard dans la base d’apprentissage \(B\) échantillons avec remise \(z_i, i = 1, \dots, B\) (chaque échantillon ayant \(n\) points).
Pour chaque échantillon \(i\) on construit un arbre CART \(G_i(x)\) selon un algorithme légèrement modifié : a chaque fois qu’un nœud doit être coupé (étape “split”) on tire au hasard une partie des attributs (\(q\) parmi les \(p\) attributs) et on choisit le meilleur découpage dans ce sous-ensemble.
Régression : agrégation par la moyenne \(G(x) = \frac{1}{B}\sum_{i=1}^BG_i(x)\).
Classement : agrégation par vote \(G(x) = \mathrm{Vote\,majoritaire\,}(G_1(x), \dots, G_B(x))\).
Les arbres sont moins corrélés car ils sont appris sur des ensembles d’attributs qui se recouvre peu (en général \(q \ll p\)).
Commentaires :
On se limite en général à des arbres pas très profonds (pour le Bagging il faut des arbres profonds pour réduire leur corrélation, mais les arbres très profonds souffrent de sur-apprentissage).
Chaque arbre est petit donc moins performant, mais l’agrégation compense pour ce manquement (chaque attribut se retrouve typiquement dans plusieurs arbres).
Comme pour le Bagging on utilise l’erreur OOB pour prévenir le sur-apprentissage (on choisit \(B\) là où l’erreur se stabilise et ne descend plus).
Paramètres (valeurs par défaut) :
Classement : \(q=\sqrt{p}\), taille nœud minimale 1 ;
Régression : \(q=p/3\), taille nœud minimale 5.
En pratique les valeurs « idéales » dépendent beaucoup de la base (et il faut les trouver par validation croisée).
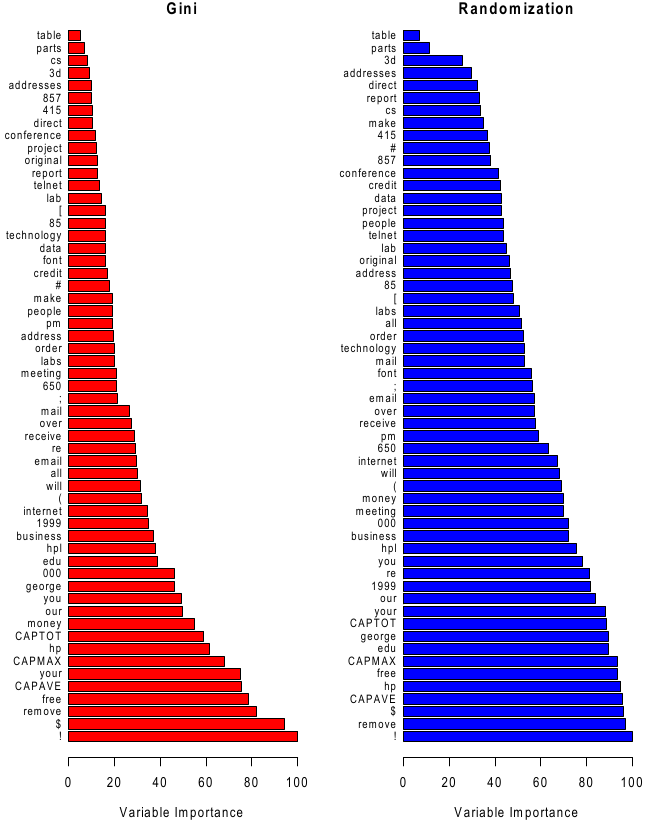
L’importance des attributs :
Les attributs peuvent être évalués pour voir leur impact dans la construction de l’arbre (mesure de Gini) ou la robustesse aux erreurs de capteurs et/ou bruit sur la classification (erreur OOB) :
Gini : Le changement dans l’impureté (ou gain d’information) dans chaque noeud où l’attribut est testé, cumulé sur tous les arbres de la foret.
Erreur OOB : après avoir construit l’arbre no \(b\), tous les échantillons OOB sont évalués et l’erreur mesurée. Ensuite on permute aléatoirement les valeurs sur chaque attribut \(j\) dans les échantillons OOB et on mesure le taux d’erreur à nouveau. La valeur finale est la dégradation moyenne (changement du taux d’erreurs) sur tous les arbres (\(b=1..B\)).
Boosting¶
Le principe du boosting est de combiner les sorties de plusieurs classifieurs faibles (weak classifier) pour obtenir un résultat plus fort (strong classifier). Le classifieur faible doit avoir un comportement de base un peu meilleur que l’aléatoire : taux d’erreurs inférieur à 0.5 pour une classification binaire (c’est-à-dire qu’il ne se trompe pas plus d’une fois sur deux en moyenne, si la répartition des classes est équilibrée). Chaque classifieur faible est pondéré par la qualité de sa classification : mieux il classe, plus il sera important. Les exemples mal classés aurons un poids plus important (on dit qu’ils sont boostés) vis-à-vis de l’apprenant faible au prochain tour, afin qu’il pallie le manque.
Un des algorithmes les plus utilisés en boosting s’appele AdaBoost, abréviation de adaptative boosting, proposé dans [FS97].
Algorithme AdaBoost¶
En entrée nous avons les éléments suivants :
Les données d’apprentissage : \((x_1, y_1), \dots, (x_n, y_n), x_i \in X, y_i \in \{-1, 1\}\) (problème de classification).
Une famille \(\mathcal{G}\) de classifieurs faibles.
Le nombre \(M\) de classifieurs faibles à mettre dans le mélange final.
A chaque échantillon d’apprentissage \(x_i\) on associe un poids \(w_i\) qui encode le degré de difficulté de cet échantillon par rapport au classifieurs faibles déjà choisis jusqu’à l’itération courante. Au départ tous les exemples d’apprentissage ont le même poids (\(w_i=1/n\) ). A chaque itération (supposons que \(m\) désigne le numéro de l’itération courante) on choisit dans \(\mathcal{G}\) le classifieur \(G_m\) qui minimise l’erreur de classement sur les données d’apprentissage pondérées par les \(w_i\). Ensuite on calcule \(\alpha_m\), la pondération de \(G_m\) dans le mélange final, on met à jour le poids \(w_i\) pour booster les éléments qui ont été mal classés et on passe à l’itération suivante. L’algorithme détaillé est donné ci-dessous.
Algorithme 1 (AdaBoost)
Initialiser les poids \(w_i = 1/n, i = 1..n\)
Pour \(m=1\) à \(M\) :
A : Choisir le classifieur \(G_m(\cdot) \in \mathcal{G}\) qui minimise l’erreur pondérée par les poids \(w_1,\dots,w_n\) sur la base d’apprentissage :
\[G_m(\cdot) = \mathrm{arg}\,\min_{G_i \in G} \sum_{i=1}^n w_i I(y_i \neq G_i(x_i))\]ou la fonction unité \(I(\cdots)\) aide à compter le nombre d’erreurs, c.t.d. \(I(y_i \neq G_i(x_i))\) retourne 1 si \(y_i \neq G_i(x_i)\) et 0 le cas contraire.
B : Calculer le taux d’erreurs :
\[e_m = \frac{\sum_{i=1}^n w_i I(y_i \neq G_i(x_i))}{\sum_{i=1}^n w_i}\]C : Calculer le poids \(\alpha_m\) du classifieur \(G_m(\cdot)\) :
\[\alpha_m = \log\left(\frac{1-e_m}{e_m}\right)\]Si le taux d’erreurs \(e_m\) est petit on est devant un bon classifieur, son poids \(\alpha_m\) dans le mélange final sera donc grand. Au contraire, un classifieur qui fait beaucoup d’erreurs, aura moins d’impact (\(\alpha_m\) petit).
D : Réajuster les poids :
\[w_i = w_i \exp(\alpha_m I(y_i \neq G_i(x_i))), i = 1 \dots, n\]Si \(x_i\) est bien classé par \(G_i\) (\(G_i(x_i) = y_i\)) alors \(w_i\) reste inchangé (car \(\exp(0)=1\)). Dans le cas contraire, \(x_i\) est un cas difficile et son poids est augmenté, d’autant plus si \(\alpha_m\) est grand (ce qui signifie qu’un bon classifieurs n’arrive pas a bien classé cet échantillon).
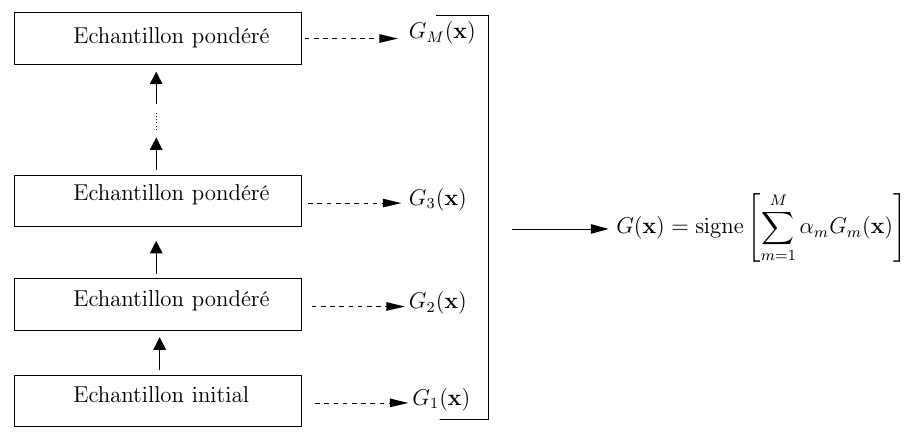
Le classifieur final est :
\[G(x) = \mathrm{signe}\left(\sum_{m=1}^M \alpha_m G_m(x)\right)\]
En bas : courbe \(\alpha_m\) vs. \(e_m\).
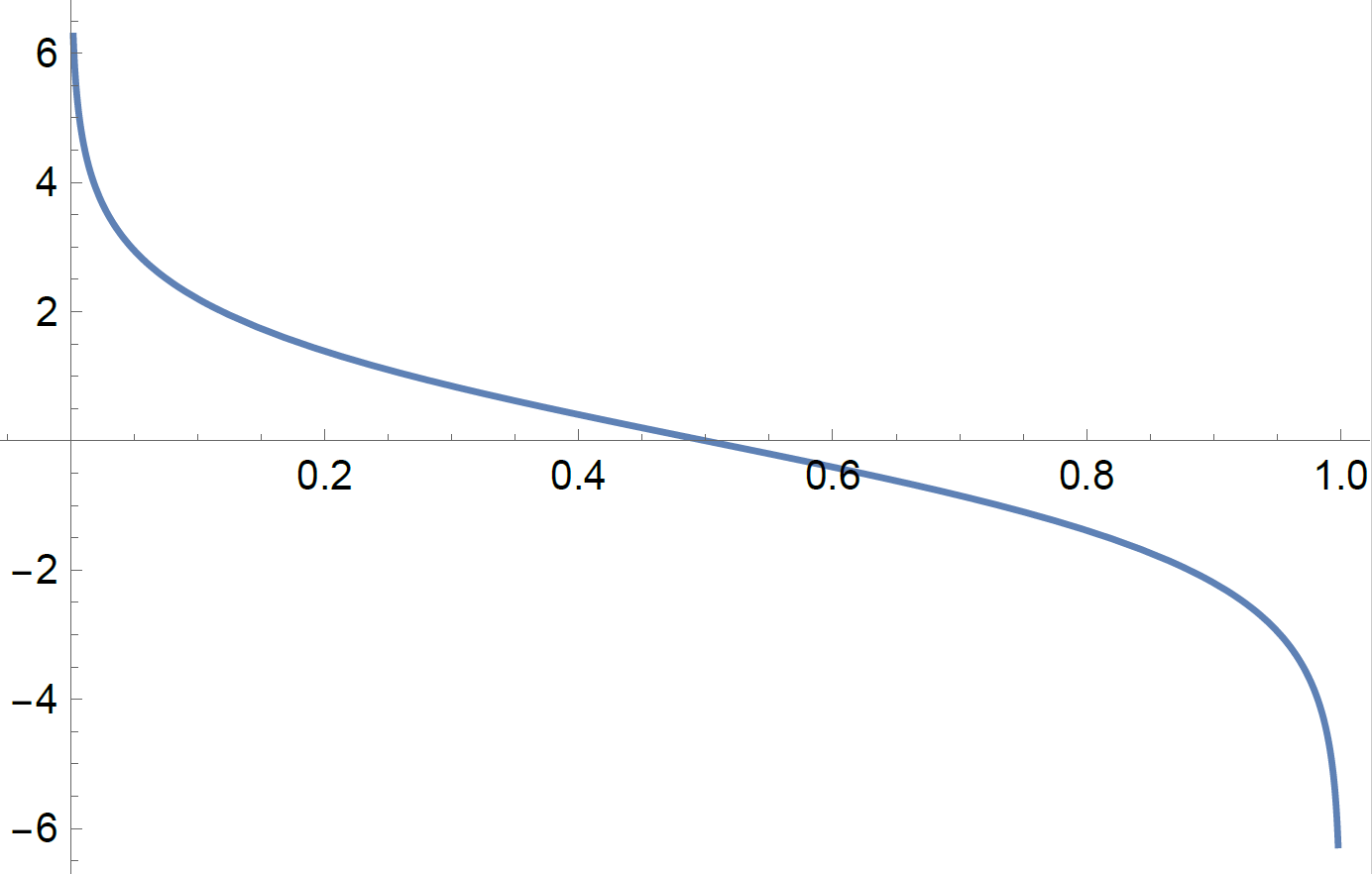
On voit que l’erreur \(e_m\) doit être inférieure à 0.5, sinon \(\alpha_m\) devient négatif, d’où la nécessité que les classifieurs faibles soit un peu meilleurs qu’un choix aléatoire.
Par la suite on va montrer que AdaBoost peut être vu comme un cas particulier de model additif (Forward Stagewise Additive Modeling) qui minimise une fonction de perte exponentielle [HTF09] (Chap. 10).
Boosting comme modèle additif¶
Un modèle additif peut être écrit comme une somme de modèles (fonctions) simples (weak learners), caractérisées par des paramètres \(\gamma_m\) :
Ces modèles sont appris en minimisant une fonction de perte \(L(\cdot)\) moyennée sur les exemples d’apprentissage :
Minimiser sur \(2M\) variables est un problème complexe qui peut rarement être résolu en pratique (\(M\) est souvent de l’ordre des centaines). Une solution est de minimiser séquentiellement par rapport a une seule paire de variables \(\beta, \gamma\) (Forward Stagewise Additive Modeling : FSAM).
Algorithme 2 : Forward Stagewise Additive Modeling
Initialiser \(f_0(x) = 0\)
Pour \(m=1\) à \(M\) :
\((\beta_m, \gamma_m) = \mathrm{arg}\,\min_{\beta, \gamma} \sum_{i=1}^n L(y_i, f_{m-1}(x_i) + \beta b(x, \gamma))\)
Mettre \(f_m(x) = f_{m-1}(x_i) + \beta_m b(x, \gamma_m)\)
A chaque itération \(m\), les paramètres \(\beta_m\) et \(\gamma_m\) sont choisis tel que le modèle courant \(f_m(\cdot)\) atteint une perte minimale sur l’ensemble d’apprentissage.
Par la suite nous montrons que AdaBoost est équivalent avec FSAM avec une fonction de perte exponentielle : \(L(y, f(x)) = \exp(-y f(x))\). Dans ce cas \(b(x_i,\gamma)\) est un classifieur \(G(x_i)\) qui produit une repose +1 ou -1. Nous avons :
\((\beta_m, \gamma_m) = \mathrm{arg}\,\min_{\beta, \gamma} \sum_{i=1}^n L(y_i, f_{m-1}(x_i) + \beta b(x, \gamma))\)
Il n’y a pas de paramètre \(\gamma\), à la place il faut choisir un classifieur \(G\in \mathcal{G}\) :
\((\beta_m, G_m) = \mathrm{arg}\,\min_{\beta, G} \sum_{i=1}^n \exp(-y_i (f_{m-1}(x_i) + \beta G(x_i)))\)
\((\beta_m, G_m) = \mathrm{arg}\,\min_{\beta, G} \sum_{i=1}^n w_i^{(m)} \exp(-\beta y_i G(x_i))\) où \(w_i^{(m)} = \exp(-y_i (f_{m-1}(x_i))\).
Les valeurs \(w_i^{m}\) ne dépendent ni de \(\beta\) ni de \(G\), on peut donc les regarder comme des valeurs pondérant chaque échantillon d’apprentissage. Par contre, les \(w_i^{m}\) dépendent du \(f_{m-1}(x_i)\), donc ces valeurs changent à chaque itération. Quelque soit la valeur du \(\beta\), le classifieur qui réalise la perte minimale est celui qui diffère de la cible \(y_i\) pour les échantillons qui ont les valeurs \(w_i^{m}\) les plus petites :
\(G_m = \mathrm{arg}\,\min_G \sum_{i=1}^n w_i^{m} I(y_i \neq G(x_i))\)
Pour obtenir \(\beta_m\) il faut donc minimiser l’expression :
\(S(\beta) = \sum_{i=1}^n w_i^{(m)} \exp(-\beta y_i G_m(x_i)) = e^{-\beta} \sum_{y_i = G_m(x_i)} w_i^{(m)} + e^{\beta} \sum_{y_i \neq G_m(x_i)} w_i^{(m)}\)
\(S(\beta) = e^{-\beta} \sum_{y_i = G_m(x_i)} w_i^{(m)} + (e^{-\beta} \sum_{y_i \neq G_m(x_i)} w_i^{(m)} - e^{-\beta} \sum_{y_i \neq G_m(x_i)} w_i^{(m)}) + e^{\beta} \sum_{y_i \neq G_m(x_i)} w_i^{(m)}\)
\(S(\beta) = (e^{-\beta} \sum_{y_i = G_m(x_i)} w_i^{(m)} + e^{-\beta} \sum_{y_i \neq G_m(x_i)} w_i^{(m)}) + (- e^{-\beta} \sum_{y_i \neq G_m(x_i)} w_i^{(m)} + e^{\beta} \sum_{y_i \neq G_m(x_i)} w_i^{(m)})\)
\(S(\beta) = e^{-\beta} \sum_i w_i^{(m)} + (e^{\beta} - e^{-\beta}) \sum_{y_i \neq G_m(x_i)} w_i^{(m)} = e^{-\beta} \sum_i w_i^{(m)} + (e^{\beta} - e^{-\beta}) \sum_i w_i^{(m)} I(y_i \neq G_m(x_i))\)
Pour trouver les valeurs extrêmes de \(S(\beta)\) on calcule la dérivé première (on met \(S'(\beta) = 0\)) et, comme les sommes ne dépendent pas de \(\beta\), on obtient :
Comme dans l’algorithme AdaBoost, on note \(e_m = \frac{\sum_i w_i^{(m)} I(y_i \neq G_m(x_i))}{\sum_i w_i^{(m)}}\), le taux d’erreurs pondérées à l’itération \(m\) et on a :
On obtient les mêmes coefficients pour les classifieurs faibles que dans l’algorithme AdaBoost à une constante près : \(\alpha_m = 2\beta_m\).
Par la suite, le modèle FSAM est mis à jour :
Les poids à l’iteration suivante vont devenir :
Comme \(-y_i G_m(x_i) = 2 I(y_i \neq G_m(x_i)) - 1\) et \(\alpha_m = 2\beta_m\), il s’ensuit que :
On ignore le terme \(\exp(-\beta_m)\) car il s’applique à tous les échantillons (il ne dépend pas de \(i\)) et on obtient la règle AdaBoost de mis-à-jour des poids \(w_i\).
En conclusion : AdaBoost minimise une fonction de perte exponentielle via un mécanisme de mis-à-jour incrémentale d’un modèle additif (Forward Stagewise Additive Modeling).
Gradient Boosting¶
Le modèles additifs séquentiels FSAM (Forward Stagewise Additive Modeling) présentés dans la section précédente considèrent la fonction de perte elle-même comme une pièce entière: lors de chaque itération, chaque apprenant ajouté et son coefficient associé sont sélectionnés de manière à ce que le nouveau modèle mis à jour (précédent + nouvel apprenant) dans son ensemble a une perte minimale.
Une méthode alternative est d’ajouter (itérativement) un nouvelle contribution dans le modèle, contribution qui diminue le « résidu » par rapport à la variable cible \(y_i\), e.g. la partie qui n’a pas pu être prise en compte par le modèle précédent. On cherche un modèle de mélange linéaire : à l’itération \(m\) on a déjà construit le modèle \(f_{m-1}(x)\) et on cherche a ajouter une contribution \(h_m(x)\) tel que \(f_m(x) = f_{m-1}(x) + h_m(x)\) et \(f_{m-1}(x_i) + h_m(x_i) = y_i\). On veut donc que les valeurs \(h_m(x_i)\) approxime bien les résidus \(y_i - f_{m-1}(x_i)\): le principe est de combler les différences entre les prédictions courantes et les valeurs \(y_i\).
Supposons qu’on utilise une perte quadratique; au début de l’étape \(m\) on a donc :
Calculons les dérivées par rapport à \(f_{m-1}\)
Dans le cas de la perte quadratique, on constate que les résidus sont donnés par l’inverse du gradient de la fonction perte :
Ensuite on apprend un classifieur faible \(h_m(x)\) sur l’ensemble d’apprentissage \(\{x_i, r_{mi}\}_{i=1}^n\), classifieur utilisé pour la mise-à-jour du modèle :
Le procédé cherche donc itérativement le modèle \(f(x)\) par une descente de gradient qui minimise la fonction de perte \(L(\cdot)\). Le paramètre \(\gamma_m\) est donné par :
L’algorithme commence avec une fonction constante \(f_0(x) = \mathrm{arg}\,\min_{\gamma} \sum_{i=1}^n L(y_i, \gamma)\) et continue pendant \(M\) itérations. Bien sûr, si la fonction de perte n’est pas quadratique, les valeurs \(r_{mi}\) ne sont plus les résidus par rapport à la cible, mais le principe reste identique : l’apprenant faible \(h_m\) « tire » le modèle \(f_{m-1}(\cdot)\) dans une direction qui minimise la fonction objectif \(L(\cdots)\). Le procédé reste le même et dans ce cas, pour garder la même terminologie, les valeurs \(r_{mi}\) sont appelés pseudo-résidus.
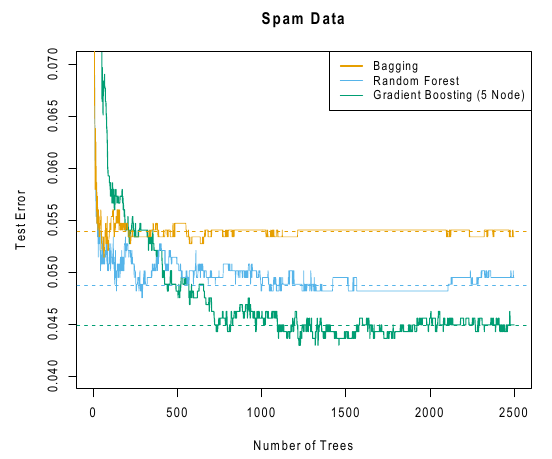
Exemple sur « Spambase »
Comparaison entre Bagging, forêts aléatoires et Gradient Boosting sur la base « Spambase ».
Références : livres et articles¶
- Bre96
Breiman et al. Bagging predictors, Machine Learning, 24(2), 1996.
- Bre01(1,2)
Breiman et al. Random forests, Machine Learning, 45, 2001.
- FS97
Freund et Schapire, A decision-theoretic generalization of on-line learning and an application to boosting, Journal of Computer and System Sciences, vol. 55, no 1, 1997, p. 119-139.
- HTF09(1,2)
Hastie, Tibshirani, Friedman, The elements of statistical learning : data mining, inference, and prediction, New York, Springer Verlag, 2009.
- Rou
Rouvière, L., Introduction aux méthodes d’agrégation : boosting, bagging et forêts aléatoires, polycopié cours, https://perso.univ-rennes2.fr/laurent.rouvier).