Le notebook de ce TP est disponible ici ou sur colab .
TP1 Séries Temporelles : Identification de modèles¶
Dans ce TP nous allons nous intéresser aux propriété de la fonction d’autocorrélation pour les processus AR et MA et voir comment interpréter cette quantité dans le but d’estumer les paramètres d’un modèle.
Introduction à l’ACF et la PACF¶
La fonction d’auto-corrélation \(\gamma(\tau)\) (AutoCorrleation Function), ACF permet d’avoir un indice de dépendance linéaire entre a série \(\{x_t\}\) à un intant \(t\) et \(\{x_{t+\tau}\}\) pour un décalage de \(\tau\).
La fonction d’auto-corrélation parielle \(\phi(\tau)\) (Partial AutoCoreelation function), PACF, donne la corrélation entre \(x_t\) et \(x_{t-\tau}\) après avoir retiré toute dépendance en \((x_{t-1},\cdots,x_{t-\tau+1})\)
Propriétés¶
Pour un modèle de type Mooving Average MA (\(q\)), l’ACF a la propriété de s’atténuer fortement pour des lags supérieur à \(q\) :
Pour un modèle de type Auto-Regressive AR (\(p\)), la PACF a la propriété de s’atténuer fortement pour des lags supérieur à \(p\) :
Question :¶
Justifier les propriétés énoncées précédement. Indice : la PACF \(\phi(x_t,x_{t-\tau})\) peut être vu comme l’ACF \(\tau(\hat x_{t} , \hat x_{t-\tau})\) avec :
c’est à dire, \(x_t\) au quel on retire son estimation par le prédicteur linéaire basé sur les \(\tau - 1\) lags précédents.
Sélection de modèle¶
Dans cette partie vous utiliserez l’ACF et la PACF pour déterminer si les données sont mieux expliquées par un modèle AR ou MA.
Commençons par télécharger le premeir jeu de données et le charger.
| y | |
|---|---|
| 2013-01-01 | 1.624345 |
| 2013-01-02 | -0.936625 |
| 2013-01-03 | 0.081483 |
| 2013-01-04 | -0.663558 |
| 2013-01-05 | 0.738023 |
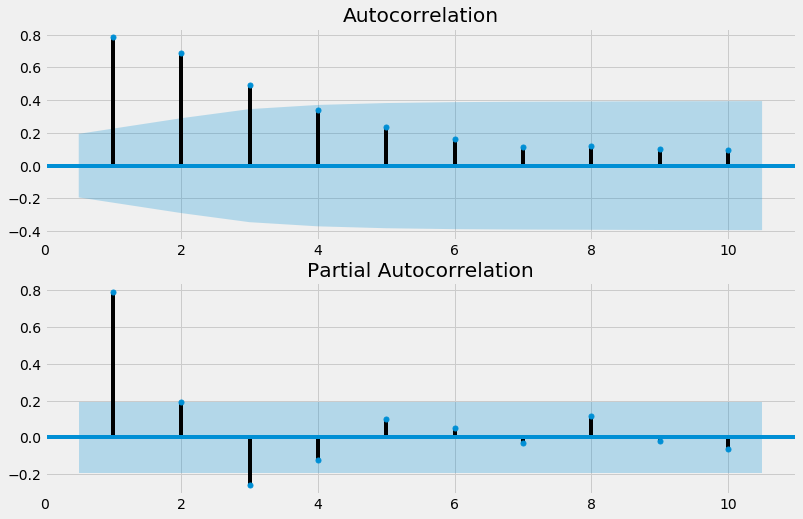
À présent, affichons l’ACF et la PACF pour cette série. Pour cela nous
utilisons les fonction plot_acf et plot_pacf de la bibliothèque
statsmodels. Vous pouvez consulter sa documentation
ici .
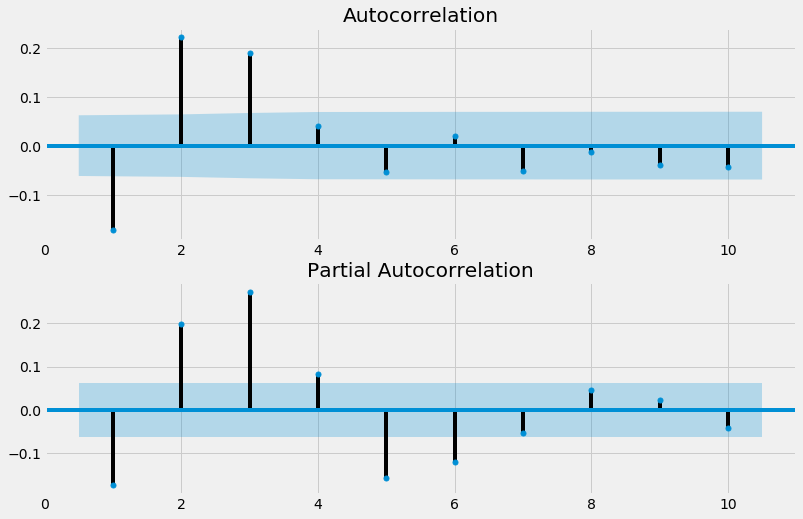
Au vue des valeurs de l’ACF et de la PACF, quel serait le meileur modèle pour expliquer les données observées ?
Magnitude sismique¶
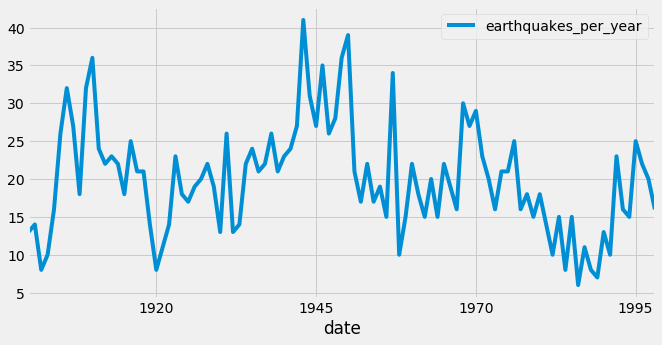
Continuons d’utiliser la même heuristique pour un nouveau jeu de données présentant les magnitudes sismiques annuelles moyennes.
Commençon par télécharger et afficher les données :
| earthquakes_per_year | |
|---|---|
| date | |
| 1900-01-01 | 13.0 |
| 1901-01-01 | 14.0 |
| 1902-01-01 | 8.0 |
| 1903-01-01 | 10.0 |
| 1904-01-01 | 16.0 |
Exercice :¶
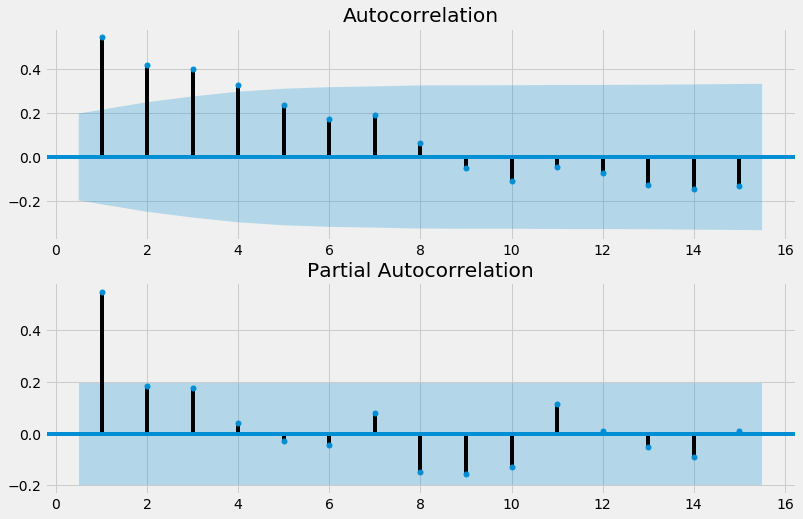
Afficher et l’ACF et la PACF pour cette série et déterminer le modèle le plus convenable
Évaluation¶
Dans cette partie nous nous intéresserons à différents critères d’erreurs pour évaluer à quel point notre modèle est pertinent.
Erreur absolue moyenne¶
L’erreur absolue moyenne MAE est souvent utilisée pour évaluer un modèle :
où \(\hat x_t\) est la baleur de \(x_t\) prédite par le modèle.
Calculons cette erreur sur la série de relevée sismiques pour voir à quel point notre modèle est bon :
4.7556256718469045
Exercice :¶
Comparer à l’erreur obtenue pour un modèle différent.
Statistique résiduelles et diagnostique¶
Un critère important en estimation de modèle est la distribution du résidu. Celui-ci ne doit pas être corrélé car le contraire indiquerait que cette erreur pourrait être prise en compte dans le modèle.
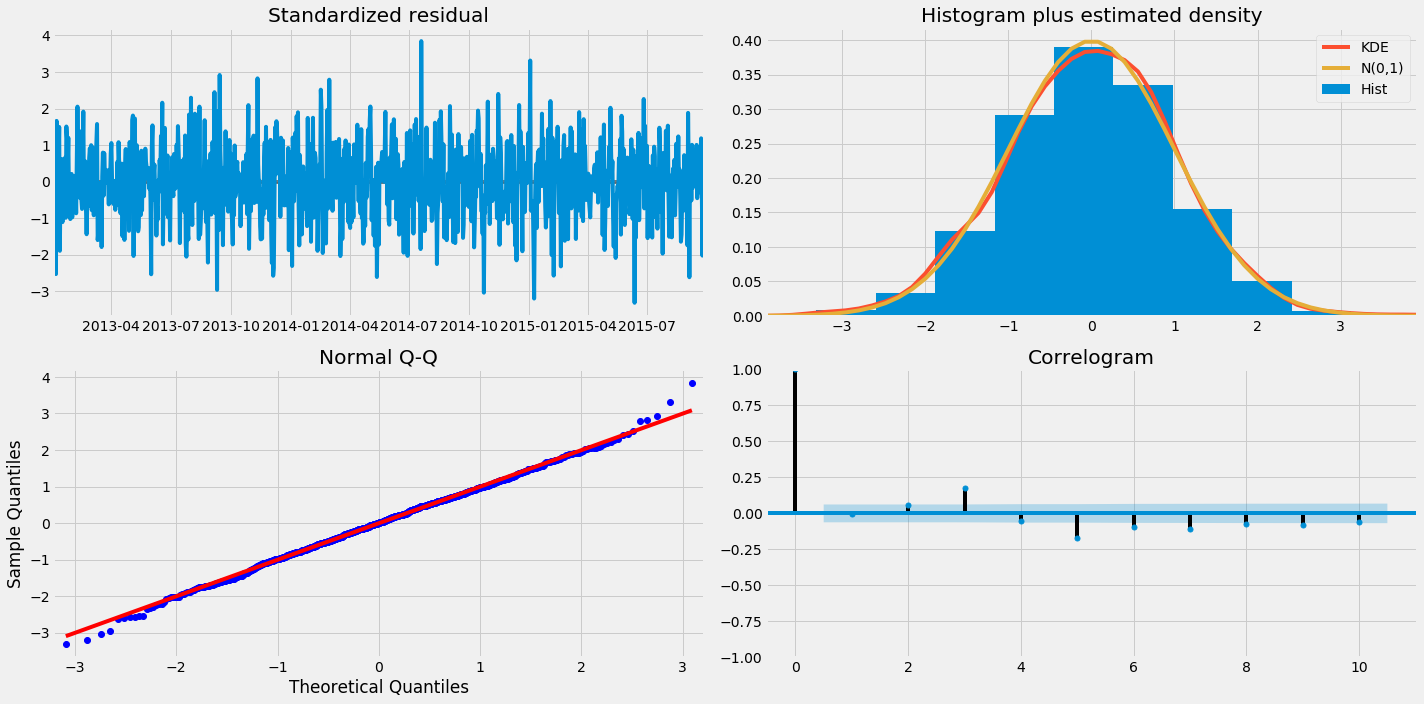
Nous nous intéresserons aux quantitées suivantes :
| Observation | Attendu |
|---|---|
| Valeur du résidu | Pas de tendance ou de périodicité |
| Histogramme et KDE | L’histogramme et l’estimation de la densité doivent être proche d’une gaussienne |
| Quantile théorique loi Normale v s. Empirique | La plupart des points sont sur la bissectrice |
| C orrelogramme | 95% des corrélations pour un lag supérieur à 1 ne sont pas significantes |
Méthode de Box-Jenkins¶

box_jenkins
La méthode Box-Jenkins est un protocole d’estimation de modèle. La première étape consiste à identifier le modèle et donc repérer toute tendance ou périodicité avant d’étudier l’ACF ou la PACF. D’autres critères tels que BIC ou AIC peuvent aussi être analysés. Une fois un modèle identifié, l’étude de l’erreur et du résidu doivent permettre de déterminer si l’estimation est bonne. Dans le cas contraire, il faut recommencer la procédure.
Identification¶
Nous allons nous intéresser à une série présentant les valeurs d’épargne des particulier en pourcentage des revenus disponibles pour la période de 1955-1979 aux USA.
La première étape est de s’assurer que le jeu de donnée ne contient ni tendance ni périodicité. Nous allons effectuer le test Dicky-Fuller pour s’en assurer. Ce test n’est pas une garantie forte mais une faible valeur de celui-ci indique l’abscence de tendance.
| savings | |
|---|---|
| date | |
| 1955-01-01 | 4.9 |
| 1955-04-01 | 5.2 |
| 1955-07-01 | 5.7 |
| 1955-10-01 | 5.7 |
| 1956-01-01 | 6.2 |
(-3.1858990962421405, 0.020815541644114133, 2, 99, {'1%': -3.498198082189098, '5%': -2.891208211860468, '10%': -2.5825959973472097}, 188.1686662239687)
0.020815541644114133
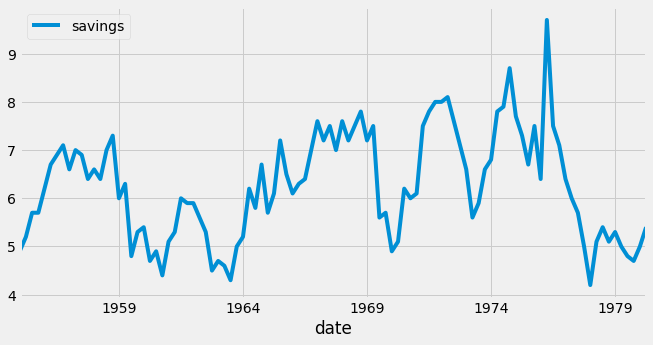
La série étudiée ne contient aucune tendance ou périodicité nécessitant de la différencier. Un processus AR, MA ou ARMA pourra donc convenir. Reste à trouver le bon modèle.
Estimation¶
L’ACF et la PACF peuvent donner des indices sur le modèle mais pour essayer d’avoir le meilleur modèle nous allons en tester plusieurs.
Exercice¶
Compléter le code suivant pour tester tout les modèle ARMA(\(p,q\))
pour des valeurs de \(p\) et \(q\) allant de 0 à 3. On utilisera
la classe SARIMAX pour créer un model ARMA et la méthode .fit()
pour l’ajuster.
0 0 313.6028657326894 318.85281135925794
0 1 267.06970976886913 274.94462820872195
0 2 232.16782676455585 242.66771801769295
0 3 217.59720511188743 230.7220691783088
1 0 216.20348062499983 224.07839906485265
1 1 215.7003896386748 226.2002808918119
1 2 207.65298608433693 220.7778501507583
1 3 209.57498691600946 225.32482379571508
2 0 213.9723232754384 224.4722145285755
2 1 213.43035679044817 226.55522085686954
/home/chanseok/anaconda3/lib/python3.7/site-packages/statsmodels/tsa/statespace/sarimax.py:963: UserWarning: Non-stationary starting autoregressive parameters found. Using zeros as starting parameters.
warn('Non-stationary starting autoregressive parameters'
2 2 209.57903436790426 225.32887124760987
2 3 211.57503208933585 229.94984178232573
3 0 209.5449310791239 222.66979514554527
3 1 210.8214763494127 226.57131322911835
3 2 211.45759881817608 229.83240851116597
3 3 213.54389994712193 234.5436824533961
Les valeurs d’AIC et BIC devrait pointer vers un modèle ARMA(1,2) comme étant le meilleur.
Diagnostique¶
Analysons le résidut pour le meilleur modèle :
SARIMAX Results
==============================================================================
Dep. Variable: savings No. Observations: 102
Model: SARIMAX(1, 0, 2) Log Likelihood -98.826
Date: Tue, 16 Jun 2020 AIC 207.653
Time: 10:54:42 BIC 220.778
Sample: 01-01-1955 HQIC 212.968
- 04-01-1980
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 1.6813 0.714 2.356 0.018 0.283 3.080
ar.L1 0.7286 0.111 6.538 0.000 0.510 0.947
ma.L1 -0.0539 0.145 -0.372 0.710 -0.338 0.230
ma.L2 0.3680 0.097 3.812 0.000 0.179 0.557
sigma2 0.4012 0.043 9.265 0.000 0.316 0.486
===================================================================================
Ljung-Box (Q): 33.59 Jarque-Bera (JB): 55.13
Prob(Q): 0.75 Prob(JB): 0.00
Heteroskedasticity (H): 2.61 Skew: 0.82
Prob(H) (two-sided): 0.01 Kurtosis: 6.20
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
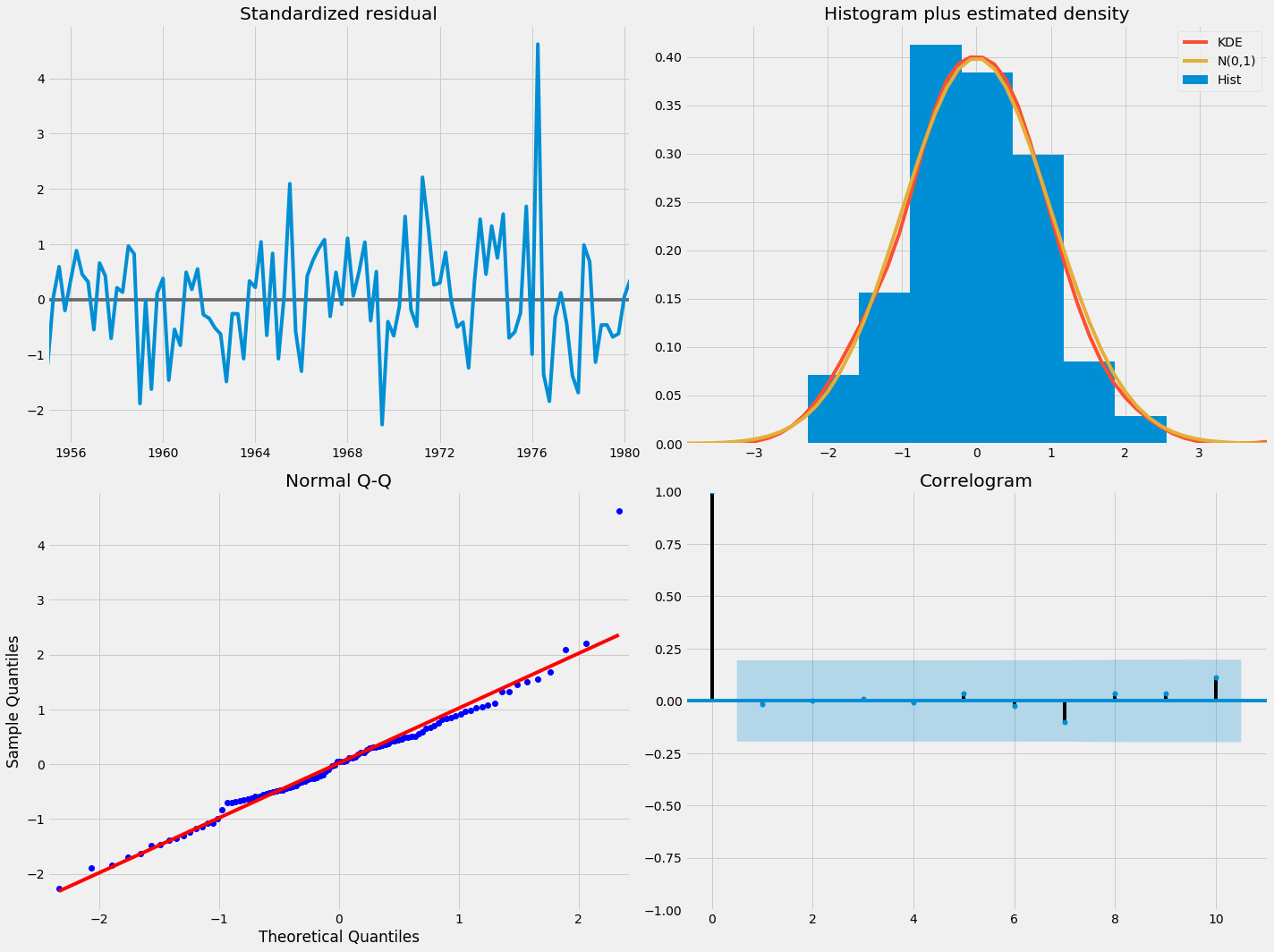
Le test Jarque-Bera contrôle la probabilité que le résidue soir distribué selon une loi normal. Ici Prob(JB):0.00 ce qui indique que cette hypothèse doit être rejetée. Toutefois, les quantiles de la distribution empirique semblent relativement proche des quantiles théorique pour une loi normale. Une valeur abérante est certaienement responsable de la mauvaise valeur du test. L’histogramme et le corrélogramme semblent également satisfaisants.