Réseaux génératifs antagonistes

Les réseaux génératifs antagonistes (on parlera de GAN pour Generative Adversarial Networks) [GPougetM+14] forment une famille de réseaux de neurones génératifs capables de capturer la distribution des données.

Les GAN se composent de deux réseaux séparés :

• un générateur \(G\), qui à partir d’un code latent \(z\) tiré aléatoirement produit une observation synthétique,

• un discriminateur \(D\), qui reçoit en entrée une observation et la classifie dans l’une des deux catégories suivantes : réelle ou synthétique.

Les deux modèles sont entraînés en opposition : le discriminateur apprend à distinguer les données issues de la véritable distribution de celles produites artificiellement par le générateur, tandis que le générateur apprend à tromper le discriminateur.

Du point de vue du discriminateur, on cherche à maximiser la fonction objectif qui permet de séparer les valeurs du logit de sortie pour les données réelles (sortie positive) des valeurs du logit pour les données synthétiques (sortie négative) :

\[\max_\phi \mathbb{E}_{x\sim p(x)} \log D_\phi(\mathbf{x}) + \mathbb{E}_{\hat{\mathbf{x}} \sim p(\hat{\mathbf{x}})} [\log(1 - D_\phi(\hat{\mathbf{x}}))]\]

avec \(\hat{\mathbf{x}} = G_\theta(\mathbf{z})\)

Tandis que pour le générateur, nous cherchons à minimiser cette quantité. Comme \(\theta\) n’intervient que dans le terme de droite, la fonction objectif à minimiser pour le générateur est :

\[\min_\theta \mathbb{E}_{\mathbf{z} \sim p(\mathbf{z})} [ \log(1 - D_\phi(G_\theta(\mathbf{z})))]\]

Au bout du compte, l’optimisation du GAN est donc un jeu minimax défini par la fonction objectif :

(6)\[\min_\theta \max_\psi V(G_\theta, D_\psi) = \overbrace{\underbrace{\mathbb{E}_{\mathbf{z} \sim p(\mathbf{z})} [ \log(1 - D_\phi(G_\theta(\mathbf{z})))]}_\text{générateur} + \mathbb{E}_{\mathbf{x} \sim \textbf{p}_\text{data}} [ \log D_\phi(\mathbf{x}) ]}^\text{discriminateur}\]

Algorithme d’optimisation

Le générateur transforme un bruit \(z \in \mathcal{N}(0,1)^n\) en une observation synthétique \(\mathbf{\hat{x}}\), c’est-à-dire que l’on tire au hasard un code latent selon une loi normale dans l’espace \(\mathcal{Z}\) de dimension \(n\). On pourrait choisir d’autres lois de probabilité (par exemple, une distribution uniforme) mais la loi normale est la plus commune.

L’objectif de \(G\) est d’apprendr à tromper le discriminateur, c’est-à-dire produire des observations \(\mathbf{\hat{x}}\) tells que \(p(\mathbf{\hat{x}}) = p(G(\mathbf{z})) \approx p(\mathbf{\hat{x}})\) et donc que la distribution des données synthétiques soit indifférenciable des données réelles.

Le discriminateur classe les observations \(\mathbf{\hat{x}}\) en deux catégories : réelles ou artificielles. Sa sortie est constitué d’un seul neurone dont la fonction d’activation est une sigmoïde :

\[f(x) = \frac{1}{1 + e^{-x}}\]

qui prend ses valeurs dans l’intervalle \([0,1]\). Par convention, on étiquette les données réelles avec un score de 1 et les données synthétiques avec un score de 0.

L’optimisation du générateur et du discriminateur s’effectue en alternance. Une itération de l’algorithme d’apprentissage du GAN peut se décrire de la façon suivante :

1. Échantillonner \(m\) données réelles \(x_1, \dots, x_m \in \mathcal{D}\)

2. Échantillonner \(m\) vecteurs de bruit \(z_1, \dots, z_m \sim p_z\)

3. Appliquer une itération de descente de gradient sur les paramètres \(\theta\) du générateur :

\[\nabla_\theta V(G_\theta, D_\phi) = \frac{1}{m} \nabla_\theta \sum_{i=1}^m \log(1 - D_\phi(G_\theta(z_i))\]

4. Appliquer une itération de montée de gradient sur les paramètres \(\phi\) du discriminateur :

\[\nabla_\phi V(G_\theta, D_\phi) = \frac{1}{m} \nabla_\phi \sum_{i=1}^m \left[\log D_\phi(x_i) + \log(1 - D_\phi(G_\theta(z_i)))\right]\]

Justification théorique

\[\min_\theta \max_\psi V(G_\theta, D_\psi) = \overbrace{\underbrace{\mathbb{E}_{\mathbf{z} \sim p(\mathbf{z})} [ \log(1 - D_\phi(G_\theta(\mathbf{z})))]}_\text{générateur} + \mathbb{E}_{\mathbf{x} \sim \textbf{p}_\text{data}} [ \log D_\phi(\mathbf{x}) ]}^\text{discriminateur}\]

Considérons un générateur \(G_\theta\) fixé. On optimise alors uniquement le disriminateur \(D_\phi\) pour réaliser la classification binaire des observations entre réelles et synthétiques. La fonction objectif à optimiser est donc :

\[\max_\phi \int_x (p_\text{réelles}(x) \log D(x) + p_\text{fausses} \log(1 - D(x))) dx\]

Cette fonction objectif admet pour maximum :

\[D_\phi^* : x \rightarrow \frac{p_\text{réelles}(x)}{p_\text{réelles}(x) + p_\text{fausses}(x)}\]

La valeur optimale de \(V\) est donc :

\[\min_\theta V(G_\theta, D^*) = \int_x \left( p_r(x) \log \frac{p_r(x)}{p_r(x) + p_f(x)} + p_f(x) \log \frac{p_f(x)}{p_r(x) + p_f(x)} \right) dx\]

On peut montrer que :

\[\min_\theta V(G, D^*) = 2 D_\text{JS}(p_r || p_f) - 2 \log 2\]

où \(D_\text{JS}\) est la divergence de Jensen-Shannon, définie par la formule suivante :

\[D_{JS}[p_r, p_f] = \frac{1}{2} \left(D_{KL} \left[p_r, \frac{p_r + p_f}{2}\right] + D_{KL} \left[ p_f, \frac{p_r + p_f}{2} \right] \right)~~.\]

L’optimisation du générateur revient donc à minimiser la divergence Jensen-Shannon entre la distribution des données réelles \(p_r\) et la distribution des données synthétiques \(p_f\).

Cette propriété émerge de façon indirecte dans l’optimisation des GAN. On considère généralement que les GAN sont des modèles génératifs implicites, par opposition à d’autres modèles tels que les mélanges gaussiens ou les auto-encodeurs variationnels où l’apprentissage de la distribution latente passe par une maximisation explicite de la vraisemblance.

Dans les réseaux antagonistes, le discriminateur \(D\) fait office de test permettant de juger si les deux distributions (réelle et générée) sont statistiquements différentes. Autrement dit, \(D\) définit une mesure de distance implicite entre les deux distributions. Le discriminateur tente de maximiser cette distance tandis que le générateur \(G\) s’efforce de la réduire.

Wasserstein GAN

Comme nous venons de le voir, la formulation du GAN introduite par Goodfellow et al. [GPougetM+14] revient implicitement à minimiser une divergence entre la distribution des données réelles et la distribution approchée par le générateur du GAN. Toutefois, la divergence de Jensen-Shannon hérite des inconvénients de la divergence de Kullback-Leibler dont elle est dérivée: - la divergence KL est nulle lorsque les supports des deux distributions sont disjoints, - la divergence KL n’est généralement pas différentiable, ni continue.

Mais les divergences ne sont pas les seules fonctions capables de caractériser la dissimilarité entre deux distributions. Il existe au moins deux autres fonctions pouvant servir de distances entre probabilités: la variation totale (dont nous ne parlerons pas) et la distance de Wasserstein (ou Earth-Mover distance). La distance de Wasserstein entre deux distributions \(p_r\) réelle et \(p_f\) fausse est obtenue par:

(7)\[W(p_r, p_f) = \inf_{\gamma \in \Pi(p_r, p_f)} \mathbb{E}_{(x,y)\sim \gamma} \left[x - y \right]\]

avec \(\Pi(p_r, p_f)\) l’ensemble de toutes les distributions jointes \(\gamma(x,y)\) dont les marginales sont égales à \(p_r\) et \(p_f\). Intuitivement, la distribution jointe \(\gamma(x,y)\) représente la « masse » qui est transportée de chaque point \(x\) vers chaque point \(y\), de sorte à ce que la distribution \(p_r\) soit transformé en la distribution \(p_f\). La distance de Wasserstein cherche alors le transport qui minimise le coût de cette transformation. Il s’agit ainsi du transport optimal entre \(p_r\) et \(p_f\).

Cette distance \(W\) est intéressante à deux titres. D’une part, elle croît linéairement avec la distance entre les moyennes des distributions, même si \(p_r\) et \(p_f\) sont disjointes. D’autre part, elle est continue et même différentiable par rapport aux paramètres \(\theta\) de \(p_f\) lorsque cette distribution est supposée gaussienne. Cela rend la distance de Wasserstein appropriée pour une optimisation par descente de gradient, par exemple.

Cependant, pour trouver le minimum de l’équation (7), il faudrait pouvoir parcourir toutes les distributions conjointes \(\Pi(p_r, p_f)\), ce qui est intractable. Toutefois, la dualité de Kantorovich-Rubinstein nous donne une autre façon de calculer la distance de Wasserstein:

(8)\[W(p_r, p_f) = \frac{1}{K} \sup_{\lVert f \rVert_L \leq K} \mathbb{E}_{x\sim p_r}[f(x)] - \mathbb{E}_{x\sim p_f}[f(x)]\]

pour \(f\) appartenant à l’ensemble des fonctions K-lipschitziennes, c’est-à-dire vérifiant la condition:

\[\forall (x_i, x_j), ~~ |f(x_i) - f(x_j)| \leq K |x_i - x_j| ~~.\]

Qu’est-ce que ceci signifie pour les GAN ? Dans notre cas, \(p_r\) est la distribution des données réelles (\(x\sim p(x)\)) et \(p_f\) est la distribution des données synthétiques (\(G(z), z \sim p(z)\)). Notre idée est de chercher les poids du discriminateur \(D_\phi\) qui maximise une certaine distance entre \(p_r\) et \(p_f\), et les poids du générateur \(G_\theta\) qui minimise cette même distance.

Supposons que notre discriminateur \(D_\phi\) soit contraint au sous-ensemble des fonctions K-lipschitziennes. Alors, d’après (8), une façon de calculer la distance de Wasserstein entre \(p_r\) et \(p_f\) est de calculer:

(9)\[L(p_r, p_f) = W(p_r, p_f) = \max_{\phi} \mathbb{E}_{x\sim p_r} [D_\phi(x)] - \mathbb{E}_{z\sim p(z)}[D_\phi(G_\theta(z))] ~~.\]

Cette quantité peut être approchée via une estimation sur un batch de \(m\) observations:

\[L(p_r, p_f) = \frac{1}{m} [D_\phi(x) - D_\phi(G_\theta(z))]\]

Nous pouvons alors définir le Wasserstein-GAN [ACB17] comme le GAN optimisant le jeu minimax:

\[\min_\theta \max_\phi \frac{1}{m} [D_\phi(x) - D_\phi(G_\theta(z))]\]

sous réserve que le discriminateur \(D_\phi\) soit restreint au cas K-lipschitzien.

Cette contrainte peut être obtenue de deux façons:

• l’approche initiale de Arjovsky et al. [ACB17] consiste à restreindre tous les poids \(\phi\) à une norme comprise entre \([-c, +c]\) (approche dite de clipping),

• par une pénalité ad hoc sur le gradient rétropropagé dans le discriminateur [GAA+17].

GAN conditionnels

Comme dans le cas des auto-encodeurs variationnels, les réseaux génératifs antagonistes fournissent un modèle de la distribution \(p(x)\) au travers de son processus d’échantillonnage. Pour générer de nouvelles observations \(\hat{x}\), il suffit d’échantillonner des codes latents \(z \sim p(z)\) et de les décoder à l’aide du générateur :

\[\hat{x} = G(z)\]

Néanmoins, comme pour les auto-encodeurs variationnels, le contrôle que nous avons sur la génération de nouvelles données est faible. En effet, même si nous connaissons la distribution latente \(p(z)\), rien n’impose que des transformations géométriques dans l’espace latent \(\mathcal{Z}\) soient sémantiquement interprétables dans l’espace des observations \(\mathcal{X}\). Qui plus est, nous disposons parfois d’une information additionnelle \(y\) qui vient s’ajouter à l’observation \(x\). Cette information peut être l’appartenance à une classe (« chat » ou « chien »), la hauteur d’un accord ou encore les valeurs précédentes d’une séquence. Afin de structurer l’espace latent et de pouvoir contrôler plus finement la génération, il peut être intéressant de conditionner les distributions à cette information.

Concrètement, cela revient donc à s’intéresser à \(D(x|y)\) et \(G(z|y)\), c’est-à-dire en remplaçant dans l’équation (6) au jeu minimax:

(10)\[\min_\theta \max_\psi V(G_\theta, D_\psi) = \overbrace{\underbrace{\mathbb{E}_{\mathbf{z} \sim p(\mathbf{z|y})} [ \log(1 - D_\phi(G_\theta(\mathbf{z}, y)))]}_\text{générateur} + \mathbb{E}_{\mathbf{x} \sim \textbf{p}_\text{data}} [ \log D_\phi(\mathbf{x}, y) ]}^\text{discriminateur}\]

Cette formulation donne lieu au GAN conditionnel (conditional GAN ou cGAN) [MO14]. En pratique, il suffit de modifier l’architecture du GAN de sorte à ce que:

• le générateur prenne en entrée à la fois le vecteur \(z\) (code latent) et le conditionnement \(y\), par exemple en concaténant les deux variables s’il s’agit de vecteurs;

• le discriminateur prenne en entrée à la fois une observation \(x\) (réelle ou fausse) et le conditionnement \(y\).

GAN avec classifieur auxiliaire

Le GAN avec classifieur auxiliaire (Auxiliary Classifier GAN ou ACGAN) [OOS17] est une variation du GAN conditionnel introduite spécifiquement dans le cas où le conditionnement \(y\) est une variable nominale, typiquement une information de classe.

La fonction de coût du discriminateur est divisée en deux parties :

\[ \begin{align}\begin{aligned}\begin{split} L_S &= \mathbb{E}_{x\sim p(x)} \log D_\phi(\mathbf{x}) + \mathbb{E}_{\hat{\mathbf{x}} \sim p(\hat{\mathbf{x}})} [\log(1 - D_\phi(\hat{\mathbf{x}}))]\\L_C &= \mathbb{E}_{x\sim p(x)} [\log P(C = c | x)] + \mathbb{E}_{z \sim p(z)} [\log P(C = c | G_\theta(z, c))] \end{split}\end{aligned}\end{align} \]

\(L_S\) est la fonction de coût habituelle du discriminateur qui sépare les logits des observations réelles \(\mathbf{x}\) de ceux des observations générées \(\hat{\mathbf{x}}\). \(L_C\) est une fonction de coût de classification qui vérifie: - que pour une observation réelle \(x\) appartenant à la classe \(c\), alors le discriminateur assigne correctement la plus haute probabilité à la classe \(c\) parmi toutes les classes; - la même chose pour chaque observation synthétique \(\hat{x}\) obtenue en tirant un code latent \(z\) conditionné à \(c\).

Autrement dit, le discriminateur doit désormais classer les observations en vraies ou fausses, mais aussi leur assigner la bonne classe (soit par rapport à la vérité terrain, soit par rapport au conditionnement choisi).

Le discriminateur \(D_\phi\) est entraîné pour maximiser la quantité \(L_S + L_C\) tandis que le générateur \(G_\theta\) est entraîné pour maximiser \(L_C - L_S\) (les observations générées doivent appartenir à la bonne classe \(c\), mais doivent aussi tromper le discriminateur quant à leur nature réelle ou synthétique).

Cette variante ne diffère qu’assez peu du GAN conditionnel décrit ci-dessus mais est réputée stabiliser l’apprentissage du modèle. La séparation de la discrimination réel/faux d’une part et la reconnaissance de la classe d’autre part permet de rétropropager un gradient plus riche. Par ailleurs, cette approche permet de réutiliser des modèles pré-entraînés pour la classification comme discriminateurs, comme des modèles entraînés sur ImageNet pour la classification d’images.

Architectures des réseaux génératifs antagonistes

GAN convolutifs

Les premiers succès majeurs des GAN ont eu lieu dans le domaine de la génération d’images. L’introduction des Deep Convolutional Generative Adversarial Networks (DCGAN) [RMC16] utilisant une architecture convolutive ont rapidement permis d’appliquer les réseaux génératifs antagonistes sur de grandes bases de données d’images.

Le générateur du DCGAN est entièrement convolutif. Le code latent \(z\) est initialement un vecteur de dimension \(p=100\), qui est projeté par une couche entièrement connectée en un vecteur de dimension \(16384=4\times4\times1024\). Ce vecteur est ensuite redimensionné sous forme de tenseur \((4,4,1024)\) qui servira de base à notre future image. Afin d’augmenter les dimensions spatiales de l’image, le générateur utilise des convolutions à pas fractionné (souvent appelées convolutions transposées et parfois, à tort, déconvolutions). Après plusieurs convolutions, le tenseur final a pour dimensions \((W, H, C)\) avec \(W\) la largeur de l’image souhaitée et \(H\) sa hauteur. \(C\) correspond au nombre de canaux voulus, généralement 3 dans le cas d’une image rouge-vert-bleu (RGB).

Le discriminateur reprend l’architecture standard des CNN utilisés pour la classification.

Stabilisation de l’apprentissage du GAN

Compte-tenu de la nature antagoniste de l’optimisation minimax, les GAN sont généralement assez instables et leur optimisation peut s’avérer délicate et sensible au choix des hyperparamètres. L’expérience et plusieurs études empiriques ont permis de mettre à jour quelques lignes directrices à suivre pour éviter les principaux écueils.

L’objectif commun de la plupart des ces « astuces » est de rendre les gradients rétropropagés du discriminateur vers le générateur le plus riche possible. En effet, le générateur ne dispose que ces gradients indirects pour apprendre. Or, de mauvais choix d’architectures au niveau du discriminateur peuvent rendre le gradient en entrée du discriminateur souvent nul, ce qui ralentit l’apprentissage.

Les couches de pooling sont plutôt à proscrire car elles introduisent de la sparsité au niveau des gradients (par exemple, une couche de maxpooling ne rétropropage qu’à la valeur maximale). Il est préférable de les remplacer par des convolutions avec un pas équivalent à celui du pooling.

Pour la même raison, il est souhaitable de remplacer les activations non-linéaires ReLU du discriminateur par des variantes dont le gradient est partout non-nul, pour éviter les phénomènes de neurones morts. Un remplacement communément mis en œuvre est le Leaky ReLU, dont la partie négative a une pente non-nulle.

La dernière couche du générateur peut exploiter une fonction d’activation qui contraint les valeurs de sortie à être dans la bonne plage de valeurs. Par exemple, si les observations que l’on souhaite générer sont à valeur dans \([-1,+1]\) (respectivement dans \([0,1]\)), on pourra appliquer une activation \(\text{tanh}\) sur les valeurs de sortie (respectivement une sigmoïde).

La batch normalization est généralement appliquée à la fois sur le générateur et le discriminateur. Dans ce cas, on évitera de mélanger des observations réelles et synthétiques au sein d’un même batch: soit toutes les données du batch sont réelles, soient elles sont toutes fausses.

PatchGAN

Jusqu’à présent, le discriminateur utilisé dans les GAN est un classifieur binaire : une observation \(\tilde{x}\) est prédite comme étant globalement réelle ou synthétique. Cependant, cette information est sparse. Dans le cas, par exemple, de la génération d’images, il est possible que seulement une région présente des artefacts typiques d’une image générée, tandis que toutes les autres régions sont vraisemblables. Dans ce cas, comment informer le générateur que seule une partie de l’image générée doit être modifiée ? Une solution consiste à densifier les prédictions du discriminateur : c’est le modèle PatchGAN.

Le discriminateur PatchGAN est un discriminateur entièrement convolutif. Il correspond à un CNN dont on a omis les couches entièrement connectées. Ainsi, la sortie de PatchGAN est un tenseur de dimensions \((W', H')\), avec le plus souvent \((W', H') = (\lfloor \frac{W}{8} \rfloor, \lfloor \frac{H}{8} \rfloor)\), c’est-à-dire une carte de prédiction à résolution 1:8 par rapport aux images d’entrée. La fonction de coût du discriminateur est alors calculée en sommant sur toutes les positions de la carte de prédiction.

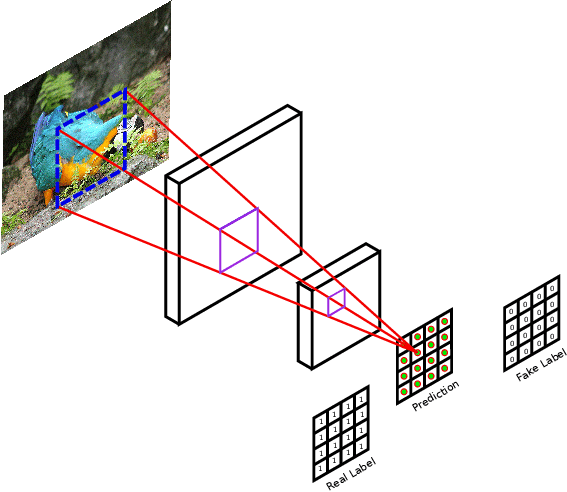
Illustration du discriminateur PatchGAN.

Par exemple, si la sortie de PatchGAN est une matrice de prédictions de dimensions \((4\times4)\), la vérité terrain sera une matrice de même dimension contenant l’étiquette correspondante répétée autant de fois que nécessaire :

\[\begin{split}\mathcal{L}(D_\phi; \mathbf{x}) = \operatorname{KL}\left( \underbrace{\begin{pmatrix} 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ \end{pmatrix}}_\text{vérité terrain ``image réelle''} - \underbrace{\begin{pmatrix} 0.1 & 0.2 & 0.1 & 0.1\\ 0.4 & 0.6 & 0.4 & 0.2\\ 0.3 & 0.5 & 0.3 & 0.2\\ 0.1 & 0.2 & 0.1 & 0.1\\ \end{pmatrix}}_\text{sortie du discriminateur} \right) = \sum_{i,j} \operatorname{KL}(D_\phi(\mathbf{x})[i,j], y^*)\end{split}\]

où \(y^*\) est l’étiquette valan 0 pour vrai, 1 pour faux.

Pix2Pix

Pix2Pix est une architecture de GAN conditionnel pour la transformation image vers image. Il part du principe qu’il existe un jeu de données appairé \(\mathcal{D} = \{(\mathbf{x}_1^{(A)}, \mathbf{x}_1^{(B)}), (\mathbf{x}_2^{(A)}, \mathbf{x}_2^{(B)}), \dots, (\mathbf{x}_n^{(A)}, \mathbf{x}_n^{(B)})\}\) d’images provenant de deux domaines, A et B. L’objectif est d’apprendre la transformation \(\Psi : A \rightarrow B\). Pour ce faire, Pix2Pix utilise comme générateur \(G\) un réseau de neurones d’architecture U-Net et PatchGAN comme discriminateur \(D\). U-Net a pour intérêt de produire en sortie une image de mêmes dimensions que l’image d’entrée, ce qui est exactement ce que l’on cherche.

La fonction de coût de Pix2Pix comporte deux termes :

()\[\mathcal{L}(G, D) = \lambda \sum_{i = 1}^n \underbrace{\lVert G(\mathbf{x}_i^{(A)}) - \mathbf{x}_i^{(B)}\rVert}_\text{reconstruction} + \mathcal{L}_\text{cGAN}(G, D)\]

où \(\mathcal{L}_\text{GAN}(G, D)\) désigne la fonction de coût adversaire du GAN conditionnel :

\[\mathcal{L}_\text{GAN}(G, D) = \sum_{\mathbf{x}_B \in B} \log D(\mathbf{x}_B) + \sum_{\mathbf{x}_A \in A} \log \left(1 - D(G(\mathbf{x}_A)) \right)~~.\]

Le premier terme de la fonction de coût () est une simple fonction de coût de régression (typiquement, une distance L1 ou L2). Elle correspond à « l’attache aux données » : une image du domaine A doit ressembler à son image correspondante dans le domaine B une fois transformée par \(G\). Le second terme ajoute une régularisation adversaire : les images générées doivent être vraisemblables par rapport à la distribution des images du domaine B. En pratique, \(\lambda\) est un hyperparamètre permettant de contrôler l’importance donner au premier ou au second terme. Ces deux fonctions de coût sont complémentaires. En effet, on observe empiriquement que la reconstruction L1 ou L2 tend à produire des images « floues », c’est-à-dire que la reconstruction se focalise sur les basses fréquences. Cependant, l’utilisation d’un discriminateur PatchGAN permet de raffiner les régions locales de l’image pour leur donner un aspect plus vraisemblable, en injectant des hautes fréquences similaires à celles qui existent dans les images du domaine B. Ainsi, l’image générée finale est de meilleure qualité qu’en utilisant une seule des deux fonctions de coût.

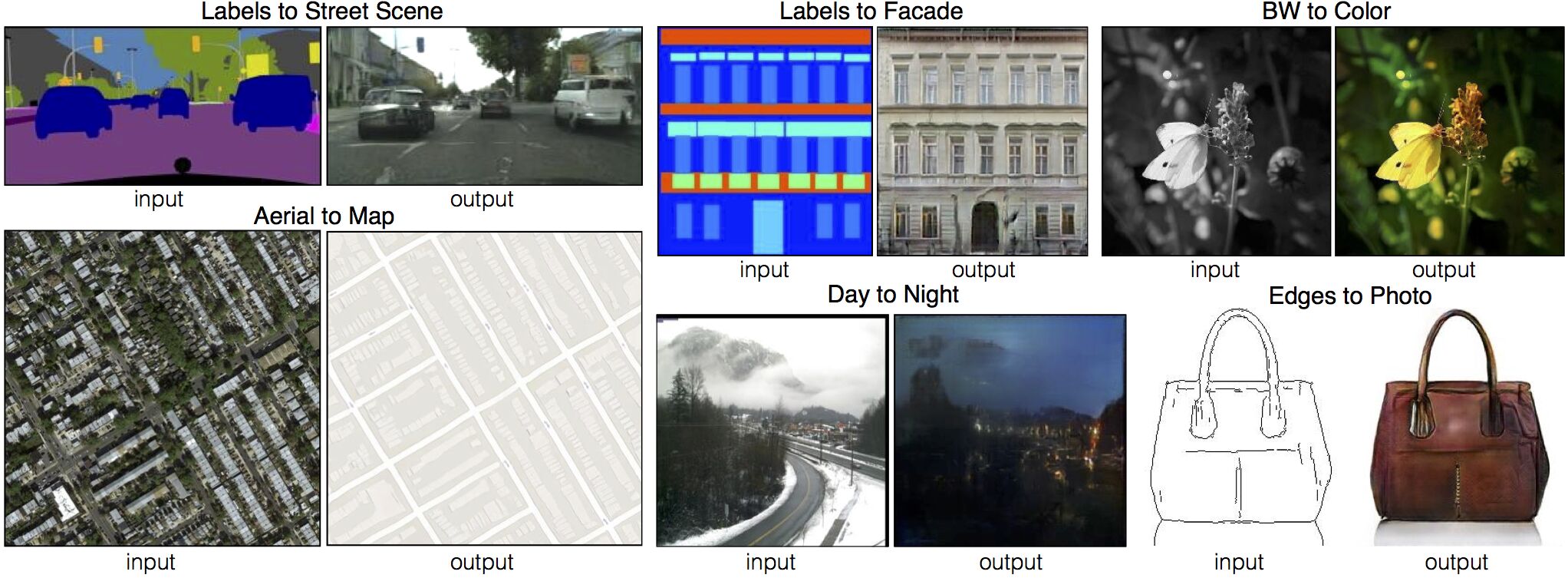
Quelques résultats qualitatifs obtenus par Pix2Pix.

Note

Contrairement aux GAN présentés jusqu’ici, Pix2Pix n’injecte pas de bruit \(z\) dans le générateur. Ce bruit est remplacé par du Dropout dans le générateur U-Net. Il est possible d’ajouter ce bruit, soit en concaténant une matrice de bruit gaussien à l’image d’entrée \(\mathbf{x}^{(A)}\), soit en l’ajoutant sur l’image. En pratique, l’ajout de bruit n’a que peu d’influence : la transformation apprise tend à être rendue déterministe par le terme de reconstruciton L1.

CycleGAN

Une limitation du modèle Pix2Pix est la nécessité d’avoir un jeu de données d’images appairées. La plupart du temps, les domaines A et B sont représentés par des jeux de données d’images qui ne s’alignent pas (par exemple, des photographies et des peintures de Frida Kahlo ne représentent généralement pas la même chose). Pour contourner ce problème, CycleGAN reprend la même architecture que Pix2pix mais introduit la supervision par cohérence cyclique. Formalisons. Soient \(X = \{x_1, x_2, \dots, x_n\}\) et \(Y = \{y_1, y_2, \dots, y_m\}\) deux jeux de données d’images de domaines différents. CycleGAN apprend les deux transformations \(G : X \rightarrow Y\) et \(F : Y \rightarrow X\), sous forme de GAN :

\[ \begin{align}\begin{aligned}\mathcal{L}_\text{GAN}(G, D_Y, X, Y) = \sum_{i=1}^m \log D_Y(y_i) + \sum_{i=1}^n \log\left(1 - D_Y(G(x))\right)\\\mathcal{L}_\text{GAN}(F, D_X, Y, X) = \sum_{i=1}^n \log D_X(x_i) + \sum_{i=1}^n \log\left(1 - D_X(G(y_i))\right)\end{aligned}\end{align} \]

où \(D_X\) et \(D_Y\) sont les discriminateurs entraînés respectivement sur les domaines \(X\) et \(Y\).

En plus de cette optimisation habituelle, CycleGAN impose une contrainte de cohérence cyclique. Par principe, transformer une image de \(X\) en image de \(Y\), puis l’image obtenue en image de \(X\) doit revenir sur la même image. Autrement dit, appliquer \(F\) puis \(G\) doit donner la fonction identité (et inversement).

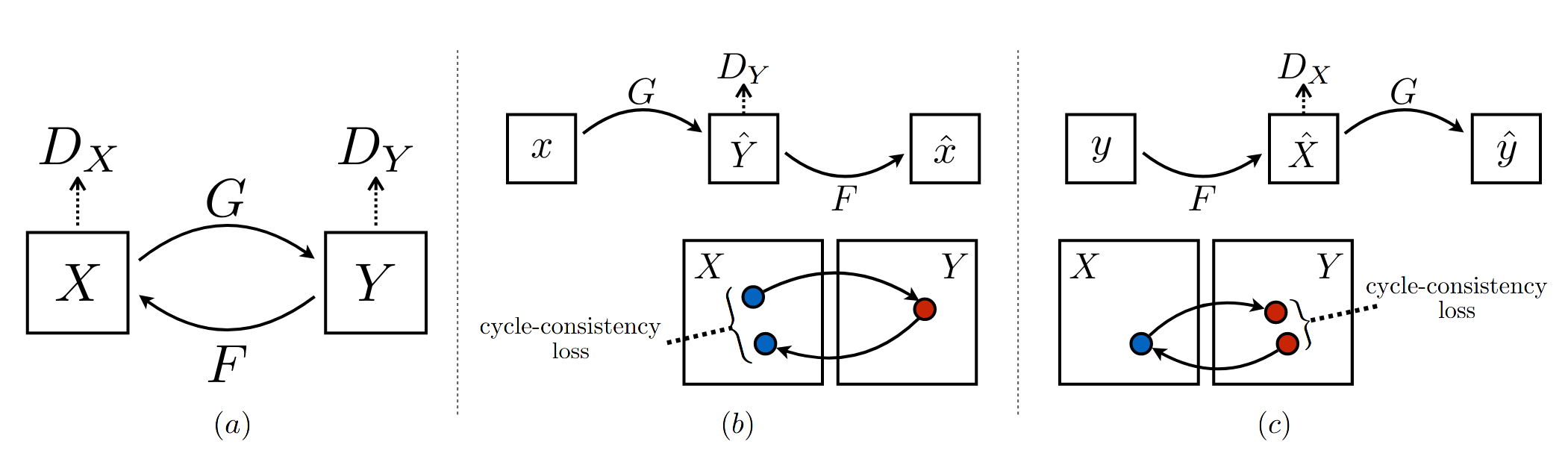
Illustration de la contrainte de cohérence cyclique de CycleGAN.

Cette propriété est contrainte dans le modèle CycleGAN par deux termes d’erreur :

\[\mathcal{L}_\text{cycle} = \sum_{i=1}^n \lVert F(G(x)) - x\rVert_1 + \sum_{i=1}^m \lVert G(F(y)) - y\rVert_1\]

Le problème d’optimisation final s’écrit alors comme la somme pondérée des fonctions de coût :

\[G^*, F^* = \arg\min_{G,F} \max_{D_X, D_Y} \mathcal{L}(G, F, D_X, D_Y) = \mathcal{L}_\text{GAN}(G, D_Y; X, Y) + \mathcal{L}_\text{GAN}(F, D_X; Y, X) + \lambda \mathcal{L}_\text{cycle}(G, F)\]

où \(\lambda\) est comme à l’accoutumée un facteur contrôlant l’importance des deux objectifs.

Quelques résultats qualitatifs obtenus par CycleGAN.

StyleGAN

StyleGAN est une architecture de GAN qui introduit un espace latent intermédiaire, entre l’espace latent du bruit \(\mathbf{z}\) et l’espace des images \(\mathbf{x}\). Cet espace, noté \(\mathcal{W}\), est appelé espace des styles.

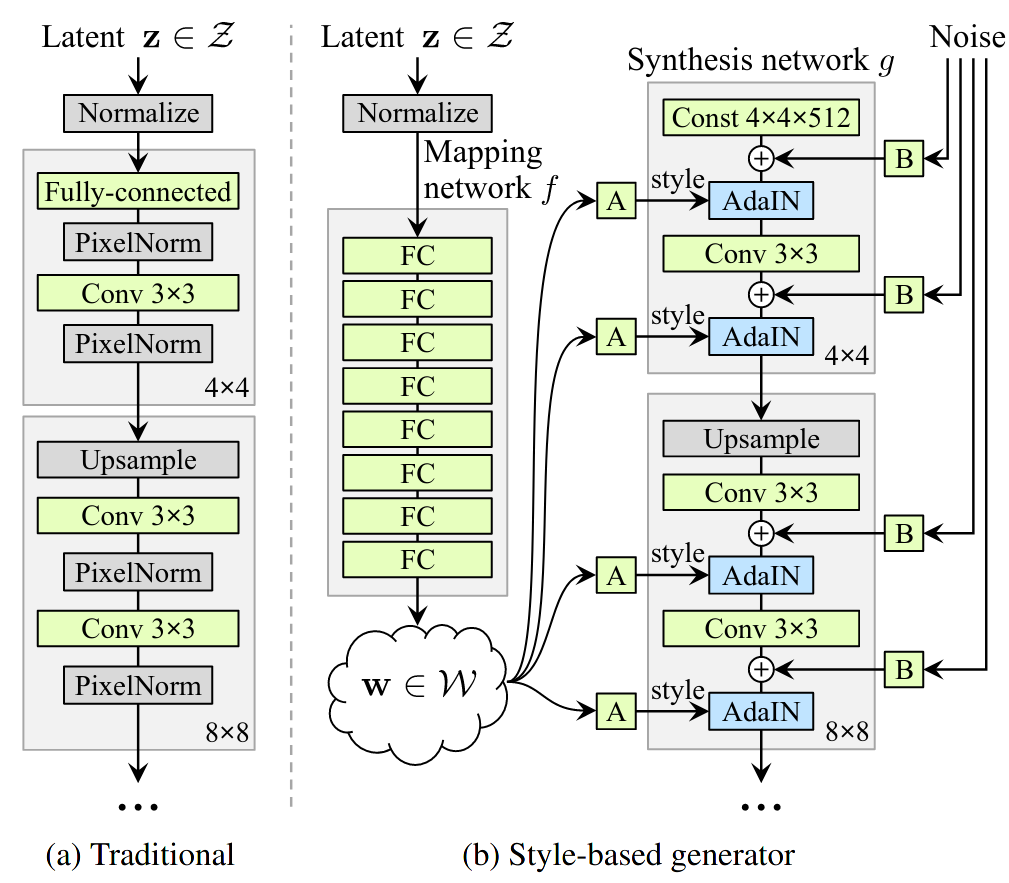
Comparaison de l’architecture habituelle du générateur dans un GAN convolutif (à gauche) et de l’architecture du générateur dans StyleGAN. Le générateur de StyleGAN introduit un mapping network, un perceptron multi-couche qui transforme le bruit initial \(\mathbf{z}\) en un vecteur de style \(\mathbf{w} \in \mathcal{W}\). Dans le schéma, A désigne une transformation affine apprise et B est une multiplication terme à terme avec un vecteur de mise à l’échelle.

En pratique, StyleGAN utilise un espace de style de dimension 512. Ce vecteur de style est ensuite injecté à chaque couche du générateur \(G\) à travers l’opération AdaIn, ou Adaptive Instance Normalization. AdaIN est une couche de normalisation qui applique une transformation affine :

\[\operatorname{AIN}(\mathbf{x_i}, \mathbf{y}) = \mathbf{y}_{s,i} \cdot \frac{\mathbf{x_i} - \mu(\mathbf{x_i})}{\sigma(\mathbf{x_i})} + \mathbf{y}_{b,i}\]

où \((\mathbf{y}_{s,i}, \mathbf{y}_{b,i}) = A(\mathbf{w}_i)\) avec \(A\) une transformation affine apprise pour la couche considérée, \(\mu(\mathbf{x_i})\) désigne la moyenne de \(\mathbf{x_i}\) et \(\sigma(\mathbf{x_i})\) sa variance. Les vecteurs \(\mathbf{y} = (\mathbf{y}_{s,i}, \mathbf{y}_{b,i})\) sont appelés les styles correspondant au vecteur latent \(\mathbf{w}\).

L’avantage de l’espace \(\mathcal{W}\) par rapport à l’espace latent \(\mathcal{Z}\) est qu’il est obtenu par une transformation non-linéaire et ne suit donc pas forcément une distribution gaussienne. Cela permet ainsi de mieux capter la structure de la distribution des images, qui est généralement fortement multi-modale. En pratique, pour renforcer le rôle des « styles », on combine les vecteurs \(y\) obtenus pour différents \(\mathbf{x}\) durant l’entraînement. Ainsi, les styles \(\mathbf{y}_{s,i}, \mathbf{y}_{b,i}\) seront aléatoirement injectés dans le générateur à la place de \(\mathbf{y}_{s,j}, \mathbf{y}_{b,j}\) et inversement.

Pour aller plus loin

Références

[ACB17] (1,2)

Martin Arjovsky, Soumith Chintala, and Léon Bottou. Wasserstein Generative Adversarial Networks. In Proceedings of the International Conference on Machine Learning (ICML), 214–223. July 2017.

[GPougetM+14] (1,2)

Ian Goodfellow, Jean Pouget, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative Adversarial Nets. In Proceedings of the Neural Information Processing Systems (NIPS), 2672–2680. 2014.

[GAA+17]

Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, and Aaron C. Courville. Improved Training of Wasserstein GANs. In Proceedings of the Neural Information Processing Systems (NIPS), 5769–5779. 2017.

[HMP+16]

Irina Higgins, Loic Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir Mohamed, and Alexander Lerchner. Beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. In International Conference on Learning Representations. November 2016.

[KW13]

Diederik P. Kingma and Max Welling. Auto-Encoding Variational Bayes. In International Conference on Learning Representations. December 2013.

[KW19]

Diederik P. Kingma and Max Welling. An Introduction to Variational Autoencoders. Foundations and Trends in Machine Learning, 12(4):307–392, 2019. arXiv:1906.02691, doi:10.1561/2200000056.

[MO14]

Mehdi Mirza and Simon Osindero. Conditional Generative Adversarial Nets. arXiv:1411.1784 [cs, stat], November 2014. arXiv:1411.1784.

[OOS17]

Augustus Odena, Christopher Olah, and Jonathon Shlens. Conditional image synthesis with auxiliary classifier GANs. In Proceedings of the 34th International Conference on Machine Learning - Volume 70, ICML'17, 2642–2651. Sydney, NSW, Australia, August 2017. JMLR.org.

[RMC16]

Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. In 4th International Conference on Learning Representations. Puerto Rico, May 2016. arXiv:1511.06434.

[SLY15]

Kihyuk Sohn, Honglak Lee, and Xinchen Yan. Learning Structured Output Representation using Deep Conditional Generative Models. In Advances in Neural Information Processing Systems, volume 28. Curran Associates, Inc., 2015.