TP RL 2 : Model Free Prediction¶
Ce Notebook peut être téléchargé ici
Ou effectué sur Colab ici
import numpy as np
from matplotlib import pyplot as plt
from time import sleep
from IPython.display import clear_output
import math
import numpy.matlib
import random
Marche aléatoire¶
Dans cet exemple simple, nous essayons d’évaluer la fonction de valeur des états correspondant à un problème de marche aléatoire. Ici, l’agent suit une politique aléatoire et peut aller soit à gauche avec une probabilité \(p\) soit à droite avec une probabilité \(1-p\). Il existe en tout \(N\) cases sur lesquelles l’agent peut se déplacer ainsi que deux cases terminales d’où il ne peut pas repartir :
La récompense de passer d’un état à l’autre est nul exceptée pour la terminaison de droite.
Dynamic programming¶
Ce problème est suffisament simple pour pouvoir êêtre calculé à la main (cf. cours). Ceci nous permettra dans ce cas de vérifier l’estimation obtenue.
First Visit Monte Carlo¶
Une première façon d’estimer la fonction de valeur en chaque état est de générer plusieurs marches aléatoires en gardant en mémoire combien de fois les états ont été visités et pour quel valeur de retour. La moyenne du retour pour chaque état nous donne ainsi une estimation non biaisée de la fonction de valeur.
La fonction suivante donne le retour G et indique si un état à été
visité (first-visite) Ns
def MC_random_walk(i0,N):
Ns = np.zeros([N,1])
i = i0
G = np.zeros([N,1])
Ns[i] = 1
while i!=-1 and i!=N:
pi = np.random.binomial(1, .5, 1)
i = i+1 if pi==0 else i-1
if i in range(N) and Ns[i]==0:
Ns[i] = 1
elif i==N:
G[np.argwhere(Ns==1)[:,0]] = 1
return Ns, G
Coding Task¶
Complétez le code suivant pour permettre l’estimation de la fonction d’état
iter = 1000
Nb_states = 5
Ns = np.zeros([N,1])
G = 0
for i in range(iter):
##### Votre code ici #####
##########################
V = G/Ns
array([[0.15696203],
[0.3313253 ],
[0.50812408],
[0.667 ],
[0.83375 ]])
Temporal Difference-Learning¶
Plutôt que d’estimer le retour après chaque trajectoire, nous allons mettre à jour l’estimation de la fonction de valeur dès qu’un état est visité en s’appuyant sur l’équation de Bellman :
Ici, nous prendrons les discount factors \(\gamma\) et \(\alpha\) égaux à 1 .
Coding Task :¶
Complétez la fonction suivant pour l’estimation de la valeur pendant que l’agent évalue dans son environnement avec l’algorithme TD0
N = 5
def TD0_random_walk(V,i0,alpha,gamma):
i = i0
i_old = i0
R = 0
while i!=-1 and i!=N:
pi = np.random.binomial(1, .5, 1)
i = i+1 if pi==0 else i-1
if i==N:
R = 1
V[i_old] = # A compléter - arrivé à droite
elif i==-1:
V[i_old] = # A compléter - arrivé à gauche
else:
V[i_old] = # A compléter - pas fini
#print((i_old,i))
i_old = i
return V
Itérons un certain nombre d’epochs pour avoir une bonne estimation
iter = 1000
V = np.zeros([N,1])
for i in range(iter):
V = TD0_random_walk(V,3,.05,1)
print(V)
[[0.15553234]
[0.32566813]
[0.5378693 ]
[0.701708 ]
[0.84790211]]
Forward-View TD(\(\lambda\))¶
Plutôt que n’utiliser que le prochain état pour mettre à jour l’estimation de l’état courrant, Il peut être tentant de voir plus loin dans le futur pour estimer la valeur d’être dans un état particulier. L’algorithme Forward-View TD(\(\lambda\)) permet de combiner l’ensemble des estimations pouvant être faites en utilisant l’information provenant d’un, deux, trois, etc réalisations future.
def FVTD_lambda_random_walk(V,i0,lambda_,alpha,gamma):
V_new = V.copy() # Offline updates
i = i0
i_old = i
R = 0
mooves = []
Gt_lambda = np.zeros([N,1])
while i!=-1 and i!=N:
pi = np.random.binomial(1, .5, 1)
i = i+1 if pi==0 else i-1
R = 0 if i!=N else 1
mooves.append((i_old,i,R)) # position en t, postition en t+1, récompense immédiate
i_old = i
for t in range(len(mooves)):
Gn_array = []
R_sum = 0
i = mooves[t][0]
for n, m in enumerate(mooves[t:]):
now, next, R = m
R_sum += gamma**n*R
Gn_t = lambda_**n*R_sum if next==N or next==-1 else lambda_**n*(R_sum + V[next])
Gn_array.append(Gn_t)
Glambda_t = (1-lambda_)*sum(Gn_array[:-1]) + Gn_array[-1]
if i in range(N):
V_new[i] = V[i] + alpha*(Glambda_t - V[i])
#print(f' moove t = {mooves[t]}, \n Gn_array = {Gn_array}, \n Glambda_t = {Glambda_t}, \n V = {V_new}, \n')
return V_new
iter = 10000
V = 0*np.ones([N,1])
for i in range(iter):
V = FVTD_lambda_random_walk(V,2,1,.1,1)
print(V)
Vt = [1/6,2/6,3/6,4/6,5/6]
print(f'RMSE = {np.sqrt(np.mean( (V - Vt)**2 ))}')
[[0.09994937]
[0.28164025]
[0.55402685]
[0.80292355]
[0.95034747]]
RMSE = 0.3957255827604822
Backward View TD(\(\lambda\))¶
L’algorithme forward view TD(\(\lambda\)) ne peut pas produire une estimation online, c’est à dire qu’il faut attendre que l’agent ait terminé sa trajectoire pour pouvoir avoir un échantillon et mettre à jour la fonction de valeur. Une variante permettant de résoudre ce problème est l’algorithme Backward View TD(\(\lambda\)). Celui-ci garde en mémoire le nombre de passages par un état pour calculer l’erreur et mettre à jour la fonction de valeur pour l’état visité.
def BVTD_lambda_random_walk(V,i0,lambda_,gamma,alpha):
V_new = V.copy() # Offline updates
E = np.zeros([N,1])
i = i0
i_old = i
R = 0
while i!=-1 and i!=N:
E = gamma*lambda_*E
E[i] += 1
pi = np.random.binomial(1, .5, 1)
i = i+1 if pi==0 else i-1 # next state
R = 0 if i!=N else 1
delta = R - V[i_old] if i==-1 or i==N else R + gamma*V[i] - V[i_old]
V_new[i_old] += alpha*delta*E[i_old]
#print(f' moove t = {(i_old,i)}, \n E = {E}, \n V = {V_new}, \n')
i_old = i
return V_new
iter = 1000
V = np.zeros([N,1])
for i in range(iter):
V = BVTD_lambda_random_walk(V,3,.5,1,.1)
print(V)
Vt = [1/6,2/6,3/6,4/6,5/6]
print(f'RMSE = {np.sqrt(np.mean( (V - Vt)**2 ))}')
[[0.13480436]
[0.32925962]
[0.49520147]
[0.70934396]
[0.88949826]]
RMSE = 0.35661035366915894
Model Free Control¶
Pour l’instant nous avons vu deux approches Monte Carlo et TD pour estimer la fonction de valeur d’un MDP. À présent nous allons voir comment faire du contrôle, c’est à dire trouver la meilleur politique.
Lorsque le contrôle était basé sur un model, nous avons vu queune façon efficace d’estimer la politique optimale était de faire une sélection gloutonne parmis les actions pour sélectioner celles qui maximiseront la fonction de valeur. Ici, nous n’avons plus de modèle ce qui veut dire que nous n’avons pas accès aux propabilités de transitions - ou alors que nous ne nous souhaitons pas nous en préocuper. Il ne nous est donc plus possible d’être exhaustif dans le choix de nos actions et plutôt que d’estimer la fonction de valeur du MDP, nous allons estimer sa fonction d’action-valeur \(Q(s,a)\) ce qui nous affranchi de devoir connaitre explicitement les transitions.
GLIE Monte Carlo control¶
Une première façon simple d’estimer \(Q(s,a)\) est d’utiliser un échantillonnage par Monte Carlo. Pour chaque paire d’état, actions \((s,a)\) visitée, nous incrémentons un compteur et nous lui associons le retour obtenu pour une certaine trajectoire. La valeur \(Q(s,a)\) est ensuite obtenue en moyennant les différents retours pour toutes les trajectoires de l’agent.
La politique optimale est ensuite obtenue en sélectionnant de façon gloutonne l’action qui va maximiser \(Q\). Pour s’assurer d’explorer tout l’espace des états et actions et converger ainsi vers la politique optimale, la politique est parfois choisie de manière aléatoire.
#@title GridWorld Class
class GridWorld:
def __init__(self, size=(5,5), start=[2,0], end=[4,2],r=-1):
self.size = size
self.Nx, self.Ny = size
self.start = start
self.state = start
self.end = end
self.EOG = 0
self.actions = ('E','N','W','S')
self.r = r
def reboot(self):
self.state = self.start
self.EOG = 0
def go(self,action):
s = self.state.copy()
if not action in self.actions:
raise ValueError('Action should be one of the following : E, N, W or S')
elif action=='N' and s[1] < self.Ny-1:
s[1] += 1
elif action=='S' and s[1] > 0:
s[1] -= 1
elif action=='E' and s[0] < self.Nx-1:
s[0] += 1
elif action=='W' and s[0] > 0:
s[0] -= 1
self.state = s
if s == self.end:
self.EOG = 1
r = 0
else:
r = self.r
return r
def plot_grid(self):
grid = np.zeros([self.Nx,self.Ny])
x,y = self.end
grid[self.Ny-y-1,x] = -1
x,y = self.state
grid[self.Ny-y-1,x] = 1
plt.imshow(grid)
plt.show()
sleep(1)
clear_output()
#@title ActionState Class
class ActionStateTable:
def __init__(self,size,values=0,end=[4,2]):
self.Nx, self.Ny = size
self.Ns = self.Nx*self.Ny
self.actions = ('E','N','W','S')
self.Na = len(self.actions)
self.values = np.full(shape=[self.Ns,self.Na],fill_value=values)
self.end = end
def get(self,s,a):
x,y = s
ia = np.argwhere([i==a for i in self.actions])
return self.values[x*self.Ny + y,ia]
def update(self,s,a,d): # s : (0,0),...,(0,Ny-1),...,(Nx-1,Ny-1) & a : E,N,W,S
x,y = s
#print(f's = {s}')
ia = np.argwhere([i==a for i in self.actions])
self.values[x*self.Ny + y, ia] = d
def greedy(self,s):
x,y = s
ia = np.argmax(self.values[x*self.Ny + y, :])
return self.actions[ia]
def plot_table(self):
plt.xticks(np.arange(-1, self.Nx+1, 1))
plt.yticks(np.arange(-1, self.Ny+1, 1))
plt.grid( which='major')
param = {'lw':3,
'head_width':1/(self.Nx+self.Ny)}
for i in range(self.Ns):
ll = self.values[i,:]
y = i%self.Ny
x = math.floor(i/self.Ny)
if [x,y] == self.end:
continue
n = np.argmax(ll)
if n==0:
plt.arrow(x,y,.5,0,**param)
elif n==1:
plt.arrow(x,y,0,.5,**param)
elif n==2:
plt.arrow(x,y,-.5,0,**param)
elif n==3:
plt.arrow(x,y,0,-.5,**param)
#@title Trajectory Class
class Trajectory:
def __init__(self,grid,gamma=1,show=0,T=1e3):
self.grid = grid
self.G = 0
self.gamma = gamma
self.actions = grid.actions
self.show = show
self.T = T
def get_action(self,Q,s,epsilon):
pi = np.random.binomial(1, epsilon, 1)
available_actions = list(self.actions)
if s[0] == 0:
available_actions.remove('E')
if s[0] == self.grid.Nx-1:
available_actions.remove('W')
if s[1] == 0:
available_actions.remove('S')
if s[1] == self.grid.Ny-1:
available_actions.remove('N')
if pi==0:
a = Q.greedy(s)
else:
a = random.choice(available_actions)
return a
Pour commencer nous allons implémenter la version Monte-Carlo du contrôle. La fonction suivante permet de lancer une trajectoire et donne en sortie le retour et le nombre de fois qu’un état à été visité.
def MC_run(traj,Q,epsilon):
grid = traj.grid
size = grid.size
N = ActionStateTable(size=size)
G = ActionStateTable(size=size)
r = 0
t = 0
grid.reboot()
while not grid.EOG and t<traj.T:
if traj.show:
traj.grid.plot_grid()
s = grid.state
a = traj.get_action(Q,s,epsilon)
#print(f'action is {a}')
r += grid.go(a)
N.update(s,a,1)
G.update(s,a,r)
t+=1
return G, N
Coding task :¶
Compléter le code suivant pour mettre à jour la Q table ainsi \(\epsilon\) de façon à converger vers une politique optimale. On dera une mise à jour touts les 10 trajectoires.
grid = GridWorld()
traj = Trajectory(grid,show=0,T=2000)
Q = ActionStateTable(size=grid.size,values=-1e3)
G = ActionStateTable(size=grid.size,values=-1e3)
N = ActionStateTable(size=grid.size,values=1)
iter = 5000
update_every = 10
epsilon = 1
alpha = .9
for i in range(iter):
### Votre code ici ####
#######################
if i%update_every==update_every-1:
print(f'iter {i}/{iter}')
Q.values = G.values/N.values
epsilon = epsilon*0.96
print(f'epsilon = {epsilon}')
if i == iter-10:
traj.show = 1
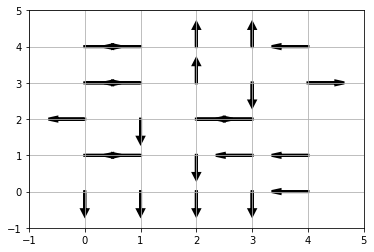
Affichons les actions sur la grille pour observer si le comportement de l’agent permet d’atteindre le but recherché (à défaut d’être réellement optimal)
Q.plot_table()
Coding task¶
A présent, complétez la fonction suivante pour permettre le contrôle avec l’algorithme SARSA
def SARSA_run(traj,Q,alpha,epsilon):
grid = traj.grid
size = grid.size
grid.reboot()
s0 = grid.state
a0 = traj.get_action(Q,s0,epsilon)
q0 = Q.get(s0,a0)
t = 0
err = 0
while not grid.EOG and t<traj.T:
if traj.show:
traj.grid.plot_grid()
r = grid.go(a0)
s1 = grid.state
a1 = traj.get_action(Q,s1,epsilon)
q1 = Q.get(s1,a1)
####### Votre code ici ####
delta =
############################
delta = min(1e2,delta) # clipping the TD error to avoid exploding gradient like phenomenon
err += delta
d = Q.get(s0,a0) + alpha*delta
Q.update(s0,a0,np.squeeze(d))
a0 = a1
s0 = s1
t+=1
return Q, err/(t-1)
L’entraînement est légèrement différent (et plus simple) qu’avec l’approche MC.
Compléter le code suivant avec l’appel à la fonction précédente pour l’entraînement
grid = GridWorld(start=[2,0],end=[2,4],r=-1e3)
traj = Trajectory(grid,show=0,T=1000)
Q = ActionStateTable(size=grid.size,values=0.,end=[2,4])
iter = 1000
update_every = 10
epsilon = 1
alpha = 1e-2
for i in range(iter):
####### Votre code ici ####
############################
if i%update_every==update_every-1:
print(f'iter {i}/{iter} , mean delta : {err/update_every}')
epsilon = epsilon*0.96
print(f'epsilon = {epsilon}')
if i == iter-10:
traj.show = 1

---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
<ipython-input-135-5b9e9ed0ca19> in <module>()
7 alpha = 1e-2
8 for i in range(iter):
----> 9 Q, err = traj.SARSA_run(Q,alpha,epsilon)
10 if i%update_every==update_every-1:
11 print(f'iter {i}/{iter} , mean delta : {err/update_every}')
<ipython-input-134-efda3da0e638> in SARSA_run(self, Q, alpha, epsilon)
85 while not grid.EOG and t<self.T:
86 if self.show:
---> 87 self.grid.plot_grid()
88 r = grid.go(a0)
89 s1 = grid.state
<ipython-input-134-efda3da0e638> in plot_grid(self)
42 plt.imshow(grid)
43 plt.show()
---> 44 sleep(.5)
45 clear_output()
46
KeyboardInterrupt:
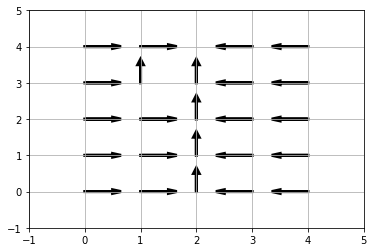
Observons la politique à présent. Vous pouvez tester différentes
configuration en faisant varier le point de départ et d’arriver dans le
gridworld correspondant aux paramètres start et end
Q.plot_table()
Coding task¶
Complétez la fonction suivante correspondant à une trajectoire avec mise à jour de la valeur suivant l’algorithme Q-Learning
def QLearning_run(traj,Q,alpha,epsilon):
grid = traj.grid
size = grid.size
grid.reboot()
t = 0
err = 0
s0 = grid.state
while not grid.EOG and t<traj.T:
if traj.show:
traj.grid.plot_grid()
####### Votre code ici ####
a0 = # action suivant la politique epsilon greedy
q0 = Q.get(s0,a0)
r = grid.go(a0)
s1 = grid.state
a1 = # action suivant la politique epsilon max
q1 = Q.get(s1,a1)
delta =
############################
delta = min(1e2,delta) # clipping the TD error to avoid exploding gradient like phenomenon
err += delta
d = Q.get(s0,a0) + alpha*delta
Q.update(s0,a0,np.squeeze(d))
s0 = s1
t+=1
return Q, err/(t-1)
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
Coding Task¶
Procédons enfin à l’entraîenemt avant d’observer la politique de l’agent
grid = GridWorld(start=[2,0],end=[2,4],r=-1e3)
traj = Trajectory(grid,show=0,T=1000)
Q = ActionStateTable(size=grid.size,values=0.,end=[2,4])
iter = 1000
update_every = 10
epsilon = 1
alpha = 1e-2
for i in range(iter):
####### Votre code ici ####
############################
if i%update_every==update_every-1:
print(f'iter {i}/{iter} , mean delta : {err/update_every}')
epsilon = epsilon*0.96
print(f'epsilon = {epsilon}')
if i == iter-10:
traj.show = 1
