Travaux pratiques - Introduction à l’apprentissage statistique¶
(correspond à 1 séance de TP)
Références externes utiles :
L’objectif de cette séance de TP est d’illustrer les séances de cours d’introduction à l’apprentissage statistique. Nous employons des données réelles et passons par les différentes étapes vues en cours :
Préparation des données¶
Les données employées sont constituées d’un bien connu ensemble de 150 observations de fleurs d’iris. Pour chaque observation sont notées la longueur et la largeur des sépales (en cm), la longueur et la largeur des pétales (en cm), ainsi que la variété d’iris (Iris Setosa, Iris Versicolo(u)r, Iris Virginica). L’objectif est de prédire la classe (la variable expliquée, ici la variété) à partir des quatre variables explicatives (longuers et largeurs des sépales et des pétales).
Dans la bibliothèque Scikit-learn nous pouvons trouver les données Iris déjà présentes. Nous pouvons les charger directement avec
# importation bibliothèque numpy
import numpy as np
# importation fonction chargement données iris
from sklearn.datasets import load_iris
donnees = load_iris()
# affichage 3 premières observations
print(donnees.data[0:3,:])
# dimensions matrice observations
print(donnees.data.shape)
# affichage étiquettes classe 3 premières observations
print(donnees.target[0:3])
# dimensions vecteur étiquettes de classe
print(donnees.target.shape)
Ou alors, pour illustrer un cas plus général, télécharger directement à partir du site le fichier de données (en format CSV, ou comma-separated values)
%%bash
wget https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data
et en lire les valeurs des quatre variables explicatives
# valeurs séparées par virgule, colonnes 0 à 3, y compris 1ère ligne
data = np.loadtxt('iris.data', delimiter=',', usecols=[0,1,2,3], skiprows=0)
print(data[0:3,:])
print(data.shape)
Les étiquettes étant sous forme textuelle dans le fichier iris.data (c’est à dire Iris-setosa, Iris-versicolor et respectivement Iris-virginica) nous tirons profit du fait que ces trois classes se succèdent dans le fichier de données et qu’il y a exactement 50 observations par classe pour générer directement des étiquettes de classe. Nous chercherons à construire un modèle permettant de séparer les iris en deux classes, Iris-versicolor et les autres (Iris-setosa et Iris-virginica). Nous utilisons alors une étiquette 1 pour Iris-setosa et une étiquette 0 pour les autres :
# générer étiquettes de classe
l1c = np.ones(50, dtype=int)
l2c = np.zeros(50, dtype=int)
target = np.concatenate((l2c, l1c, l2c))
print(target[0:3])
print(target.shape)
Dans le cas général il faudra employer une solution de conversion des étiquettes de classe adaptée à leur format. Une bibliothèque python qui propose de nombreuses fonctionalités de lecture et transformation des données est pandas.
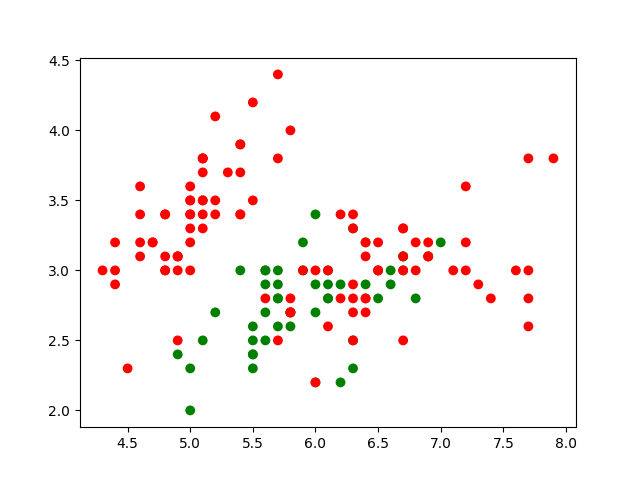
Nous pouvons visualiser les observations en nous limitant à deux ou trois variables explicatives. Par exemple, les deux premières (longueur et largeur des sépales, en cm) :
# suivant la classe, les points affichés sont rouges ou verts (green)
cmp = np.array(['r','g'])
# importer les fonctions d'affichage 2D
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(data[:,0],data[:,1],c=cmp[target],s=50,edgecolors='none')
plt.show()
Le résultat (qui devrait correspondre à la figure suivante) montre que le problème de séparation visé est très complexe si on se limite aux deux premières variables explicatives.
Pour pouvoir afficher des graphiques 3D qui peuvent être tournée avec la souris (en maintenant le click droi appuyé), il faut donner d’abord la directive suivante :
%matplotlib widget
Pour revenir à un affichage non modifiable (comme celui par défaut), la directive à utiliser est plutôt %matplotlib inline.
Question :
Affichez en 3D les observations en vous limitant aux 3 premières variables explicatives.
Choix des objectifs et fonctions d’erreur¶
Dans le cas présent les données sont très peu nombreuses, le coût des calculs sera de toute façon faible. La prédiction de la variété d’iris n’a pas d’impact sur des humains, l’aspect non discrimination n’intervient donc pas. L’interprétabilité peut toujours être utile, ici elle est dans une certaine mesure assurée par le faible nombre de variables explicatives (4) qui permet des visualisations simples. Nous nous limitons donc dans le cas présent à un critère de performance.
Pour des problèmes de classification le critère de base est le taux de bons classements (le rapport entre le nombre d’observations bien classées et le nmbre d’observations traitées). Chaque observation est donc soit bien classée (erreur égale à 0), soit mal classée (erreur égale à 1 par convention), on parle de perte 0-1 (0-1 loss). Suivant la technique de modélisation choisie, le critère de performance sera exprimé sous une forme compatible avec la technique d’optimisation employée. Dans le cas présent, l’utilisation de l’algorithme de descente de gradient demande l’emploi d’une fonction d’erreur différentiable. La forme exacte de la régularisation employée dépend également de la technique de modélisation.
Choix de la technique de modélisation¶
Nous considérons les réseaux de neurones avec une seule couche cachée, appelés aussi perceptrons multi-couches (multi-layer perceptron, MLP), qui présentent une bonne flexibilité, c’est à dire permettent d’obtenir des frontières de séparation de complexité très variable entre les classes.
Dans Scikit-learn, les perceptrons multi-couches sont mis en œuvre dans la classe sklearn.neural_network.MLPClassifier. Il est très utile d’examiner les paramètres (dont certains sont des hyper-paramètres de cette technique de modélisation, comme le nombre de neurones cachés, la fonction d’activation, la constante d’oubli alpha, etc.) de l’appel au constructeur d’une instance et aussi les valeurs par défaut employées.
La fonction d’erreur, différentiable, est l’entropie croisée et la régularisation est de type « oubli » (régularisation L2), pondérée par l’hyper-paramètre alpha.
Construction de modèles¶
Afin de pouvoir visualiser la frontière nonlinéaire de séparation entre classes, nous construisons d’abord un modèle avec des valeurs fixées pour tous les hyper-paramètres (pour la plupart celles par défaut du constructeur) en utilisant les deux premières variables explicatives.
Nous séparons d’abord les données de test et les données d’apprentissage :
from sklearn.model_selection import train_test_split
np.random.seed(10) # initialiser le générateur pseudo-aléatoire pour avoir des résultats répétables
# X : var. explicatives, y : var. expliquée, train : apprentissage, test : test
X_train1, X_test1, y_train1, y_test1 = train_test_split(data, target, test_size=0.4)
Construction d’un modèle pour illustration¶
Nous construisons ensuite le modèle :
from sklearn.neural_network import MLPClassifier
# nous utilisons l'algorithme L-BFGS pour l'optimisation
clf = MLPClassifier(solver='lbfgs')
# apprentissage avec les deux premières variables
clf.fit(X_train1[:,0:2], y_train1)
train_score = clf.score(X_train1[:,0:2], y_train1)
print("Taux de bon classement sur les données d'apprentissage : {}".format(train_score))
Nous affichons les résultats : observations d’apprentissage, observations de test, frontière de séparation. Pour déterminer la frontière de séparation, nous définissons dans le domaine de variation des deux variables explicatives une grille dense, calculons les prédictions du modèle sur tous les points de la grille et affichons un contour qui correspond aux points du plan où l’indétermination est maximale :
# créer une nouvelle figure
plt.figure()
# afficher les nuages de points apprentissage (pleins) et de test (creux)
plt.scatter(X_train1[:,0],X_train1[:,1],c=cmp[y_train1],s=50,edgecolors='none')
plt.scatter(X_test1[:,0],X_test1[:,1],c='none',s=50,edgecolors=cmp[y_test1])
# calculer la probabilité de sortie du MLP pour tous les points du plan
nx, ny = 200, 200
x_min, x_max = plt.xlim()
y_min, y_max = plt.ylim()
xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx),np.linspace(y_min, y_max, ny))
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])
Z = Z[:, 1].reshape(xx.shape)
# dessiner le contour correspondant à la frontière proba = 0,5
plt.contour(xx, yy, Z, [0.5])
plt.show()
Le résultat (qui devrait correspondre à la figure suivante) montre la séparation trouvée.
Question :
Construisez un modèle pour séparer les Iris-virginica des deux autres variétés d’iris, en utilisant seulement les deux premières variables explicatives.
Question :
Construisez un modèle pour séparer les Iris-versicolor des deux autres variétés d’iris, en utilisant cette fois toutes les variables explicatives.
Sélection de modèle¶
Nous avons regroupé ici la construction d’un ensemble de modèles avec des valeurs différentes pour les hyperparamètres et leur comparaison car dans Scikit-learn cela est réalisé en une seule instruction. Plus précisément, la construction d’un ensemble de modèles avec des valeurs pour les hyperparamètres prises dans une grille et la validation croisée pour comparer les modèles obtenus avec toutes les combinaisons de valeurs pour les hyperparamètres, Scikit-learn emploie la classe GridSearchCV qu’il faut importer.
from sklearn.model_selection import GridSearchCV
Il est ensuite nécessaire d’indiquer dans un « dictionnaire » (ou une liste de dictionnaires) quels sont les hyperparamètres dont on souhaite explorer les valeurs et quelles sont les différentes valeurs à évaluer. Chaque entrée du dictionnaire consiste en une chaîne de caractères qui contient le nom de l’hyperparamètre tel qu’il est défini dans l’estimateur employé. Pour MLPClassifier, les noms des paramètres peuvent donc être trouvés dans la présentation de cette classe. Nous considérons ici seulement trois paramètres, hidden_layer_sizes (nombre de neurones dans les couches cachées ; nous nous limitons à une seule couche), alpha (la constante \(\alpha\) de régularisation par weight decay) et activation (la fonction d’activation des neurones de la couche cachée).
tuned_parameters = {'activation': ['tanh', 'relu'],
'hidden_layer_sizes': [(5,), (20,), (100,), (150,)],
'alpha': [0.0001, 0.01, 1]}
Dans l’appel de GridSearchCV nous indiquons ensuite pour MLPClassifier le solveur à utiliser systématiquement (LBFGS, qui n’est pas celui par défaut), ensuite le dictionnaire avec les valeurs des (hyper)paramètres à explorer et enfin le fait que c’est la validation croisée k-fold avec \(k=5\) qui est employée pour comparer les différents modèles.
clf = GridSearchCV(MLPClassifier(solver='lbfgs'), tuned_parameters, cv=5)
Pour commencer, nous nous limitons encore une fois à l’utilisation des deux premières varables explicatives :
# exécution de grid search
clf.fit(X_train1[:,0:2], y_train1)
Scikit-learn exécute alors l’algorithme suivant :
à partir des listes de valeurs pour les différents hyperparamètres sont générées toutes les combinaisons de valeurs,
pour chaque combinaison, les performances des modèles correspondants sont évaluées par validation croisée 5-fold (appliquée uniquement sur les données d’apprentissage
X_train1[:,0:2], y_train1),sont sélectionnées les valeurs des hyperparamètres correspondant aux meilleures performances de validation croisée,
avec ces valeurs pour les (hyper)paramètres un nouvel apprentissage est réalisé avec la totalité des données de
X_train1[:,0:2], y_train1(et non seulement \(\frac{k-1}{k}\) folds).
Nous pouvons afficher les résultats de validation croisée obtenus pour toutes les combinaisons de valeurs pour les hyperparamètres avec clf.cv_results_. Pour visualiser les scores de validation croisée obtenus avec les différentes valeurs des hyperparamètres, nous préparons deux figures, chacune correspondant à une fonction d’activation considérée (restent deux hyperparamètres) :
n_hidden = np.array([5, 20, 100, 150])
alphas = np.array([0.0001, 0.01, 1])
# les coordonnées des points de la grille sont les valeurs des hyperparamètres
xx, yy = np.meshgrid(n_hidden, alphas)
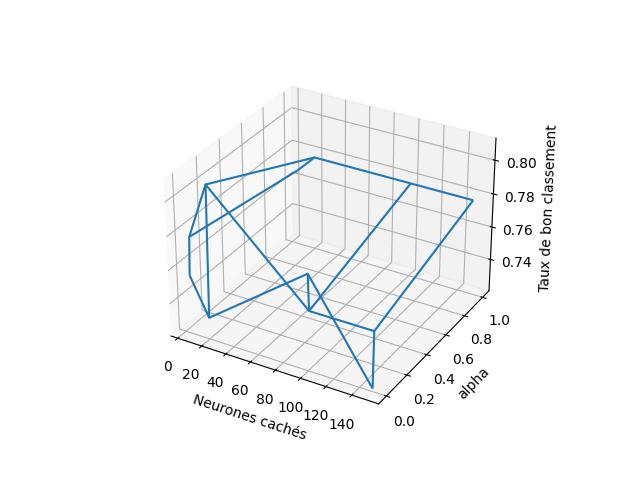
# résultats pour activation 'tanh'
Z = clf.cv_results_['mean_test_score'][0:12].reshape(xx.shape)
# affichage sous forme de wireframe des résultats des modèles évalués
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_xlabel("Neurones cachés")
ax.set_ylabel("alpha")
ax.set_zlabel("Taux de bon classement")
ax.plot_wireframe(xx, yy, Z)
plt.show()
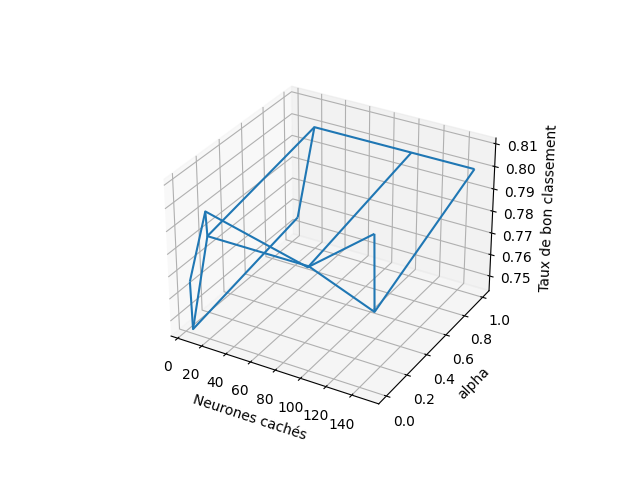
# résultats pour activation 'relu'
Z = clf.cv_results_['mean_test_score'][12:24].reshape(xx.shape)
# affichage sous forme de wireframe des résultats des modèles évalués
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_xlabel("Neurones cachés")
ax.set_ylabel("alpha")
ax.set_zlabel("Taux de bon classement")
ax.plot_wireframe(xx, yy, Z)
plt.show()
Les résultats (qui devraient correspondre aux figures suivante) montrent les performances moyennes obtenues avec chaque combinaison de valeurs pour les hyper-paramètres.
Si les graphiques montrent que les meilleurs résultats sont obtenus sur les bords des grilles, il est possible de modifier les limites de variation des hyperparamètres respectifs et relancer la recherche dans une grille ainsi ajustée.
Question :
Appliquez la recherche de la meilleure combinaison de valeurs pour les hyperparamètres en utilisant cette fois toutes les variables explicatives.
Estimation des performances futures¶
Le paramètre refit de GridSearchCV étant par défaut True, après la comparaison des modèles obtenus avec des valeurs des hyperparamètres issues de la grille, un nouveau modèle est appris sur toutes les observations d’apprentissage (sans découpage en folds) avec les meilleures valeurs trouvée pour les hyperparamètres. Ce modèle est directement accessible via l’instance de GridSearchCV (ici clf), donc pour l’évaluer sur les données de test il suffit d’écrire
clf.score(X_test1[:,0:2], y_test1)
Les performances obtenues sur les données de test sont une estimation des performances de généralisation attendues (performances sur les observations futures, supposées avoir une même distribution que les observations d’apprentissage).
Le modèle obtenu peut être enregistré dans un fichier et rechargé ensuite en mémoire à partir de ce fichier :
from joblib import dump, load
dump(clf, 'monModele.joblib')
clf2 = load('monModele.joblib')
clf.score(X_test1[:,0:2], y_test1)
clf2.score(X_test1[:,0:2], y_test1)
Cette solution doit être utilisée avec précautions et uniquement avec la version de scikit-learn qui a crée le modèle.
Pour pouvoir transférer des modèles entre logiciels différents, des formats d’échange comme ONNX et PMML ont été mis au point. Voir les explications et pointeurs sur le site de Scikit-learn.
Utilisation et surveillance du modèle¶
Une fois le modèle construit et validé (les performances futures estimées sont jugées satisfaisantes) il peut être utilisé pour prédire la classe de chaque nouvelle observation.
Il est nécessaire de procéder périodiquement à une évaluation du modèle sur de nouvelles observations. Pour cela, il faut recueillir de nouvelles observations et les faire étiqueter par un expert (ce qui a, en général, un coût), ensuite évaluer les performances du modèle sur ces nouvelles observations étiquetées pour voir si elles restent satisfaisantes. Cette évaluation se fait de la même façon que l’étape d’estimation des performances futures (les nouvelles observations remplacent les observations de test).
Le volume de nouvelles observations étiquetées doit être suffisamment élevé pour que l’évaluation du modèle soit fiable.