Deep Learning et Manifold Untangling

On va maintenant illustrer la capacité des réseaux de neurones profonds à apprendre des représentations internes capables de résoudre le problème connu sous le nom de « manifold untangling » en neuroscience, c’est à dire de séparer les exemples des différentes classes dans l’espace de représentations appris.

Pour cela, on va utiliser des outils de visualisation qui vont vont permettre de représenter chaque donnée (par exemple une image de la base MNIST) par un point dans l’espace 2D. Ces même outils vont permettre de projeter en 2D les représentations internes des réseaux de neurones, ce qui va permettre d’analyser la séparabilité des points et des classes dans l’espace d’entrée et dans les espaces de représentions appris par les modèles.

On aura besoin des modules suivants qu’on pourra importer en début de script :

import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
from scipy.spatial import ConvexHull
from sklearn.mixture import GaussianMixture
from scipy import linalg
from sklearn.neighbors import NearestNeighbors
from sklearn.manifold import TSNE

Exercice 4 : Visualisation avec t-SNE

La méthode t-Distributed Stochastic Neighbor Embedding (t-SNE) [vdMH08] est une réduction de dimension non linéaire, dont l’objectif est d’assurer que des points proches dans l’espace de départ présentent des positions proches dans l’espace (2D) projeté. Dit autrement, la mesure de distance entre points dans l’espace 2D doit refléter la mesure de distance dans l’espace initial.

On va appliquer la méthode t-SNE sur les données brutes de la base de test de MNIST en utilisant la classe TSNE du module sklearn.manifold : http://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html .

Créer un script exo1.py dont l’objectif va être d’effectuer une réduction de dimension en 2D des données de la base de test de MNIST en utilisant la méthode t-SNE.

• Créer une instance de type TSNE. N.B : on choisira 2 composantes et les paramètres suivants : init='pca' (réduire la dimension préalablement avec une ACP), perplexity=30 (lié au nombre de voisins dans le calcul des distances), verbose=2 (pour l’affichage lors de l’apprentissage).

• Appliquer la transformation pour obtenir les données projetées en 2D (fonction fit_transform). N.B : essayer tout d’abord avec un sous-ensemble de la base (e.g. 1000 exemples) pour tester l’algorithme, l’apprentissage avec l’ensemble de la base de test pouvant être long.

Métrique de séparation des classes

On va maintenant compléter le script exo4.py précédent afin de visualiser l’ensemble des points projetés en 2D, et de définir des critères pour analyser la séparabilité des classes dans l’espace projeté.

1. Calcul de l’enveloppe convexe des points projetés pour chacune des classe classe. On utilisera pour cela la la classe ConvexHull du module scipy.spatial https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.ConvexHull.html. Sur la base MNIST, on pourra donc utiliser le code suivant pour calculer les enveloppes convexes des points pour les 10 classes :

def convexHulls(points, labels):
  # computing convex hulls for a set of points with asscoiated labels
  convex_hulls = []
  for i in range(10):
    convex_hulls.append(ConvexHull(points[labels==i,:]))
  return convex_hulls
# Function Call
convex_hulls= convexHulls(x2d, labels)

où points (resp. labels) dans la méthode convexHulls(points, labels) correspond aux images projetées dans le plan 2D avec la méthode t-SNE de l’exercice 1 (resp. aux labels, i.e. classes, des images).

2. Calcul de l’ellipse de meilleure approximation des points. On utilisera pour cela la classe GaussianMixture du module sklearn.mixture http://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html#sklearn.mixture.GaussianMixture. On pourra donc utiliser le code suivant pour calculer les ellipses de meilleure approximation pour les 10 classes :

def best_ellipses(points, labels):
  # computing best fiiting ellipse for a set of points with asscoiated labels
  gaussians = []
  for i in range(10):
    gaussians.append(GaussianMixture(n_components=1, covariance_type='full').fit(points[labels==i, :]))
  return gaussians
# Function Call
ellipses = best_ellipses(x2d, labels)

3. Calcul du « Neighborhood Hit » (NH) [PNML08]. Pour chaque point, la métrique NH consiste à calculer, pour les k plus proches voisins (k-nn) de ce point, le taux des voisins qui sont de la même classe que le point considéré. La métrique NH est ensuite moyennée sur l’ensemble de la base. Le code suivant permet de calculer la métrique NH, en utilisant la classe NearestNeighbors du module sklearn.neighbors :

def neighboring_hit(points, labels):
  k = 6
  nbrs = NearestNeighbors(n_neighbors=k+1, algorithm='ball_tree').fit(points)
  distances, indices = nbrs.kneighbors(points)

  txs = 0.0
  txsc = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
  nppts = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

  for i in range(len(points)):
    tx = 0.0
    for j in range(1,k+1):
      if (labels[indices[i,j]]== labels[i]):
      tx += 1
    tx /= k
    txsc[labels[i]] += tx
    nppts[labels[i]] += 1
    txs += tx

  for i in range(10):
    txsc[i] /= nppts[i]

  return txs / len(points)

Question :

En quoi les trois métriques ci-dessus sont-elles liées au problème de la séparabilité des classes ? Qu’est-ce qui les diffère ?

Compléter le script exo4.py pour calculer les différentes métriques.

• Vous pouvez ensuite utiliser la fonction visualization suivante pour afficher les points ainsi que leur labels, et de visualiser les trois métriques précédentes :

def visualization(points2D, labels, convex_hulls, ellipses ,projname, nh):

 points2D_c= []
  for i in range(10):
      points2D_c.append(points2D[labels==i, :])
  # Data Visualization
  cmap =cm.tab10

  plt.figure(figsize=(3.841, 7.195), dpi=100)
  plt.set_cmap(cmap)
  plt.subplots_adjust(hspace=0.4 )
  plt.subplot(311)
  plt.scatter(points2D[:,0], points2D[:,1], c=labels,  s=3,edgecolors='none', cmap=cmap, alpha=1.0)
  plt.colorbar(ticks=range(10))

  plt.title("2D "+projname+" - NH="+str(nh*100.0))

  vals = [ i/10.0 for i in range(10)]
  sp2 = plt.subplot(312)
  for i in range(10):
      ch = np.append(convex_hulls[i].vertices,convex_hulls[i].vertices[0])
      sp2.plot(points2D_c[i][ch, 0], points2D_c[i][ch, 1], '-',label='$%i$'%i, color=cmap(vals[i]))
  plt.colorbar(ticks=range(10))
  plt.title(projname+" Convex Hulls")

  def plot_results(X, Y_, means, covariances, index, title, color):
      splot = plt.subplot(3, 1, 3)
      for i, (mean, covar) in enumerate(zip(means, covariances)):
          v, w = linalg.eigh(covar)
          v = 2. * np.sqrt(2.) * np.sqrt(v)
          u = w[0] / linalg.norm(w[0])
          # as the DP will not use every component it has access to
          # unless it needs it, we shouldn't plot the redundant
          # components.
          if not np.any(Y_ == i):
              continue
          plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], .8, color=color, alpha = 0.2)

          # Plot an ellipse to show the Gaussian component
          angle = np.arctan(u[1] / u[0])
          angle = 180. * angle / np.pi  # convert to degrees
          ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
          ell.set_clip_box(splot.bbox)
          ell.set_alpha(0.6)
          splot.add_artist(ell)

      plt.title(title)
  plt.subplot(313)

  for i in range(10):
      plot_results(points2D[labels==i, :], ellipses[i].predict(points2D[labels==i, :]), ellipses[i].means_,
      ellipses[i].covariances_, 0,projname+" fitting ellipses", cmap(vals[i]))

  plt.savefig(projname+".png", dpi=100)
  plt.show()

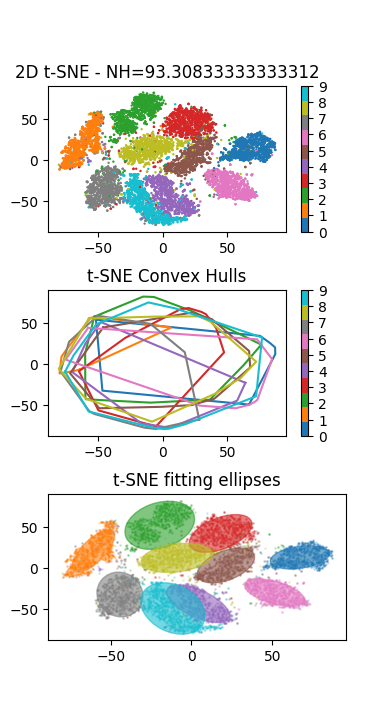
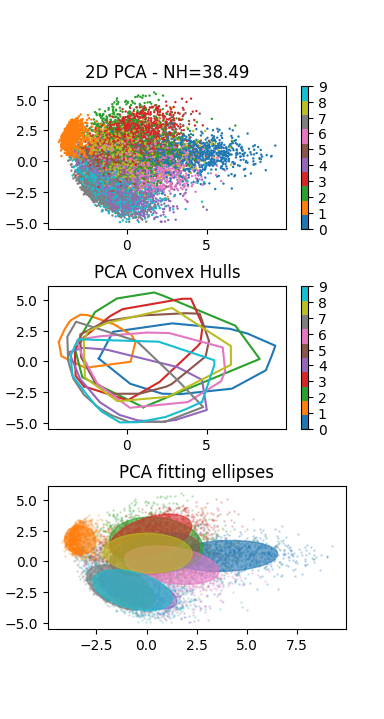
• Comparer la méthode t-SNE à une Analyse en Composantes Principales (ACP) [Hot33]. On pourra utiliser la classe PCA du module sklearn.decomposition http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html.

• L’application de la méthode visualisation sur les données de test de la base MNIST doit produire le résultat suivant (à gauche le résultat de la t-SNE à droite de l’ACP) :

• Analyser la distribution des points et des classes : que peut-on en conclure ?

Exercice 5 : Visualisation des représentations internes des réseaux de neurones

On va maintenant s’intéresser à visualisation de l’effet de « manifold untangling » permis par les réseaux de neurones.

Créer un script exo5.py dont l’objectif va être d’utiliser la méthode t-SNE de l’exercice 2 pour projeter les couches cachés des réseaux de neurones dans un espace de dimension 2, ce qui permettra de visualiser la distribution des représentations internes et des labels.

• Commencer par charger le Perceptron entraîné avec Keras dans la partie précédente, en utilisant la méthode loadModel(savename) suivante:

from keras.models import model_from_yaml
def loadModel(savename):
  with open(savename+".yaml", "r") as yaml_file:
    model = model_from_yaml(yaml_file.read())
  print "Yaml Model ",savename,".yaml loaded "
  model.load_weights(savename+".h5")
  print "Weights ",savename,".h5 loaded "
  return model

• On pourra vérifier l’architecture du modèle chargé avec la méthode summary().

• On pourra également évaluer les performances du modèle chargé sur la base de test de MNIST pour vérifier son comportement. N.B : il faudra avoir compilé le modèle au préalable.

On veut maintenant extraire la couche cachée (donc un vecteur de dimension 100) pour chacune des images de la base de test.

• Pour cela,on va utiliser la méthode model.pop() (permettant de supprimer la couche au sommet du modèle) deux fois (on supprime la couche d’activation softmax et la couche complètement connectée). Ensuite on peut appliquer la méthode model.predict(X_test) sur l’ensemble des données de test.

• Finalement, on va utiliser la méthode t-SNE mise en place à l’exercice 2 pour visualiser les représentations internes des données.

Conclure sur la capacité des réseaux de neurones à résoudre le problème du Manifold Untangling.

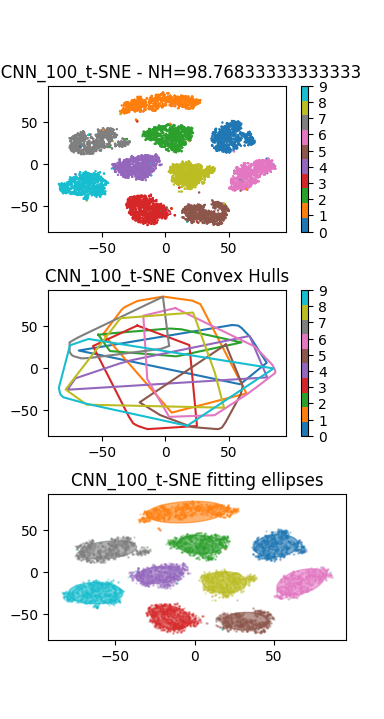
En plus du Perceptron précédent, on pourra visualiser les représentations internes apprises par un réseau convolutif de type LeNet de la partie précédente. Le résultat ci-dessous montre un résultat de visualisation obtenu avec un Perceptron (à gauche), et un réseau convolutif (à droite) :

Hot33

H. Hotelling. Analysis of a Complex of Statistical Variables Into Principal Components. Warwick & York, 1933. URL: https://books.google.fr/books?id=qJfXAAAAMAAJ.

PNML08

Fernando Vieira Paulovich, Luis Gustavo Nonato, Rosane Minghim, and Haim Levkowitz. Least square projection: A fast high-precision multidimensional projection technique and its application to document mapping. IEEE Trans. Vis. Comput. Graph., 14(3):564–575, 2008.

vdMH08

Laurens van der Maaten and Geoffrey E. Hinton. Visualizing high-dimensional data using t-sne. Journal of Machine Learning Research, 9:2579–2605, 2008.