- ... curve1
- There is a particular
case that should not be ignored:
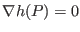 . If the gradient is zero, we
can not really say it is perpendicular to some curve. The method of Lagrangian
multipliers should check all the points where
. If the gradient is zero, we
can not really say it is perpendicular to some curve. The method of Lagrangian
multipliers should check all the points where
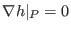 . This is described
in greater detail in [“Lagrange Multipliers Can Fail to Determine
Extrema,” College Mathematics Journal, Vol. 34, No. 1 (2003), pp. 60–62], see
https://www.maa.org/sites/default/files/nunemacher01010325718.pdf.
. This is described
in greater detail in [“Lagrange Multipliers Can Fail to Determine
Extrema,” College Mathematics Journal, Vol. 34, No. 1 (2003), pp. 60–62], see
https://www.maa.org/sites/default/files/nunemacher01010325718.pdf.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....2
- If we move away from
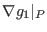 to some
other
direction
to some
other
direction 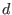 , the
hyperplane perpendicular to
, the
hyperplane perpendicular to 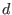 in
in 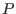 will not be tangent to the level surface
will not be tangent to the level surface
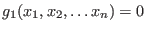 . As such, there are curves
. As such, there are curves 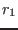 on the level surface
along which
on the level surface
along which
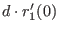 can either increase or decrease as we move in
either direction from
can either increase or decrease as we move in
either direction from 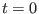 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form:3
- Care should be taken that there might be other functions
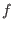 for
which
for
which 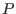 is a constrained maximum. For instance, if
is a constrained maximum. For instance, if
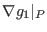 and
and
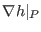 are linearly dependent, the associated surfaces have the same
supporting (tangent)
hyperplane in
are linearly dependent, the associated surfaces have the same
supporting (tangent)
hyperplane in  and the feasible area could be reduced to one point.
In such a case,
and the feasible area could be reduced to one point.
In such a case,  is the constrained optimum for any function
is the constrained optimum for any function 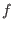 . For
instance, if
. For
instance, if
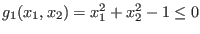 and
and
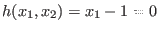 , the only
feasible point is
, the only
feasible point is 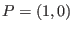 . To ensure the necessity of the KKT conditions, one
has to assume some regularity conditions.
. To ensure the necessity of the KKT conditions, one
has to assume some regularity conditions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.