Cours - Réduction de dimension¶
Ce chapitre correspond à 2 séances de cours.
Les supports écrits sont en cours de réalisation.
Réduction non-linéaire de dimension¶
Les jeux de données en haute dimension posent plusieurs problèmes lorsqu’il s’agit d’en faire une analyse descriptive. D’une part, lorsque le nombre de variables descriptives est grand, il est impossible de visualiser de façon satisfaisante ces données. D’autre part, le fléau de la dimension rend malaisée l’application des méthodes classiques de fouille de données à cause de l’éparsité des observations.
Une solution consiste à ne pas traiter la matrice d’observations originale mais plutôt à la remplacer par une représentation dans un espace de plus petite dimension, tout en conservant l’essentiel de l’information. Deux approches cohabitent :
la sélection de variables, permettant d’éliminer les variables superflues et donc de réduire le nombre de colonnes de la matrice d’observations, qui est étudiée dans le chapitre sur la sélection de variables;
la réduction de dimension, qui remplace les variables originales par un nouveau jeu de variables plus petit, que nous allons voir ici.
En réalité, la réduction de dimension a déjà été abordée dans le chapitre concernant les méthodes factorielles. L’analyse en composantes principales (ACP) est un des exemples phares de la réduction de dimension : en projetant sur les \(k\) premières composantes principales, il est possible de réduire le nombre de variables décrivant un jeu de données \(\mathbf{X}\), tout en conservant le maximum de l’information (que l’on assimile dans ce cas à la variance).
Toutefois, les méthodes factorielles sont des techniques de réduction de dimension dites linéaires, c’est-à-dire que les variables de l’espace réduit \(\{y_1, y_2, \dots, y_q\} \in \mathcal{Y}\) sont des combinaisons linéaires des variables de l’espace de départ \(\{x_1, x_2, \dots, x_p\}\). Or, ceci limite grandement les possibilités de réduction de dimension.
Locally Linear Embedding¶
Considérons une matrice d’observations \(\mathbf{X}\) de dimensions \((n, p)\), c’est-à-dire à \(n\) observations (lignes) et \(p\) variables descriptives (colonnes). L’objectif de la réduction de dimension est de déterminer \(\mathbf{\hat{X}}\) de dimension \((n, q)\) avec \(q < p\) qui représente bien la structure de \(\mathbf{X}\). Par structure, on décide notamment de s’intéresser à la propriété suivante : deux observations réduites \({x'}_i\) et \({x'}_j\) sont voisines dans l’espace d’arrivée si et seulement si les observations associées \(x_i\) et \(x_j\) dans l’espace de départ sont également voisines. Autrement dit, on souhaite que notre réduction de dimension conserve la notion de voisinage entre les observations. Ce n’est pas le seul critère qui pourrait être imaginé pour conserver l’information contenue dans le jeu de données, mais c’est celui que nous allons utiliser en pratique.
L’algorithme Locally Linear Embedding ou LLE a été introduit par [RS00] en 2000. Le principe est le suivant: localement, le nuage d’observations \(\mathbf{X}\) peut être considéré comme linéaire, c’est-à-dire engendré par un sous-espace affine. En pratique, LLE considère que chaque observation \(x_i \in \mathbf{X}\) peut-être reconstruite comme une moyenne pondérée de ses voisins \(x_{j_1}, x_{j_2}, \dots, x_{j_k}\). Dans l’espace d’arrivée, l’observation réduite correspondante \(y_i\) doit donc pouvoir être reconstruire par la même combinaison linéaire de ses propres voisins réduits \(y_{j_1}, y_{j_2}, \dots, y_{j_k}\).
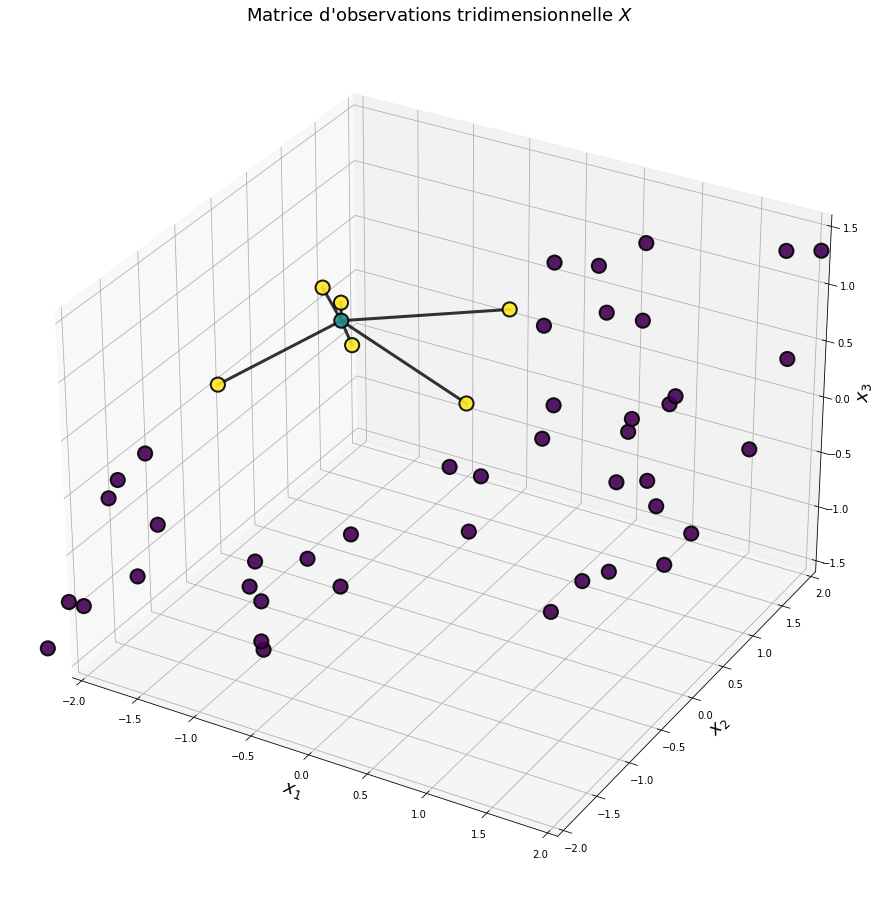
Fig. 123 Un nuage de points composé d’observations à 3 dimensions \(x = (x_1, x_2, x_3)\). Considérons une observation particulière que l’on note \(x^*\) (en bleu). Locally Linear Embedding suppose que cette observation peut se reconstruire comme une combinaison linéaire de ses voisins (en jaune) : \(x^* = \sum_k w_k x_{j_k}\). La première étape de LLE consiste à rechercher les valeurs \(w_k\) de pondération de cette combinaison linéaire.¶
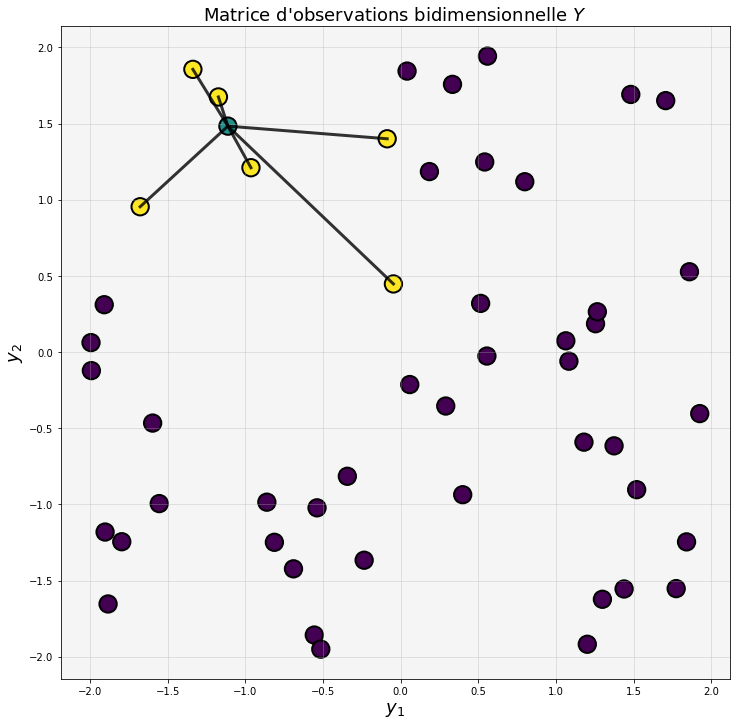
Fig. 124 Dans l’espace réduit à seulement deux dimensions, on cherche comment placer les voisins \(y_{j_k}\) (en jaune) de l’observation correspondante \(y^*\) (en bleu) de sorte à la reconstruire par la même combinaison linéaire. La deuxième étape de LLE consiste à déterminer les valeurs des coordonnées des observations réduites \(y_i\) de sorte à ce que \(y^* \approx \sum_k w_k y_{j_k}\). Les pondérations \(w_k\) sont les mêmes que celles déterminées à la première étape.¶
L’algorithme concret est donc le suivant :
Pour chaque point \(x_i \in \mathbf{X} \subset \mathbb{R}^p\)
calculer ses \(K \geq 2\) plus proches voisins de \(x_i\), notés \(V_i = \{x_{j_1}, x_{j_2}, \dots, x_{j_k}\}\)
les plus proches voisins s’obtiennent en comparant la distance euclidienne entre chaque paire \((x_i, x_j)\).
Déterminer les coefficients permettant de reconstruire chaque observation par une combinaison linéaire de ses voisins, c’est-à-dire la matrice \(\mathbf{W}^*\) de dimensions \((n,n)\) telle que
(46)¶\[\mathbf{W}^* = \arg\min_\mathbf{W} \sum_i \lVert x_i - \sum_{x_j \in V_i} w_{i,j} x_j \rVert^2\]avec la contrainte \(\sum_j w_{i,j} = 1\).
Déterminer le nuage de points réduit représenté par la matrice \(\mathbf{Y}^* \subset \mathbb{R}^q\) qui minimise l’erreur quadratique de reconstruction, c’est-à-dire
(47)¶\[\mathbf{Y}^* = \arg\min_\mathbf{Y} \sum_i \lVert y_i - \sum_{y_j \in V_i} w^*_{i,j} y_j \rVert^2 ~~,\]ce qui revient déterminer les valeurs des coordonnées réduites des observations \(y_i\) qui se reconstruisent par la même combinaison linéaire \(\mathbf{W}^*\) de leurs voisins.
Remarquons que dans l’équation (46), la matrice \(\mathbf{W}\) des pondérations qui minimise l’erreur de reconstruction est indépendante de l’échelle. En effet, multiplier toutes les coordonnées par une constante \(\lambda\) multiplie les distances par ce même facteur, mais ne change pas les relations de voisinages. Il existe donc une infinité de solutions possibles, toutes les matrices de type \(\lambda \mathbf{W}^*\). La contrainte \(\sum_j w_{i,j} = 1\) permet d’obtenir l’unicité de la solution.
Le problème décrit par l’équation (46) est un problème d’optimisation aux moindres carrés. Ce problème admet une solution analytique qui se calcule directement à partir de la matrice de covariance locale calculée sur le \(K\)-voisinage de \(x\).
Le problème décrit par l’équation (47) se résoud quant à lui par le calcul des vecteurs propres d’une matrice bien choisie, dépendant uniquement de \(\mathbf{W}\).
Pour plus de détails concernant ces deux étapes d’optimisation, consulter les annexes A et B de [SR00].
Illustration¶
Pour mieux comprendre l’effet de Locally Linear Embedding, nous prenons prendre un exemple-jouet régulièrement utilisé en réduction de dimension. Le « Gâteau roulé » (ou Swiss Roll, roulé suisse) est un jeu de données contenant des observations en trois dimensions. Néanmoins, bien qu’en trois dimensions, ce jeu de données peut être « déroulé » sur un plan bidimensionnel. Il existe donc une représentation naturelle de ce jeu de données à trois variables dans une version à seulement deux variables.
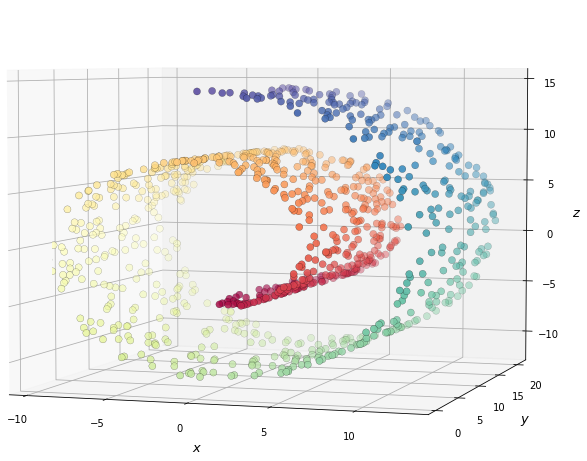
Fig. 125 Le jeu de données du « Gâteau roulé » (Swiss Roll) représente un rectangle 2D enroulé sur lui-même. Les couleurs permettent d’identifier les voisinages et ne sont présentes qu’à titre indicatif.¶
À titre de comparaison, nous pouvons appliquer une analyse en composantes principales (ACP) sur le Swiss Roll. Les directions qui expliquent le plus de variance ne sont néanmoins assez peu représentatives. En effet, la transformation qui permet de passer du gâteau roulé à trois dimensions à son alter ego déroulé n’est pas linéaire et l’ACP ne permet donc pas de construire une projection l’approchant.
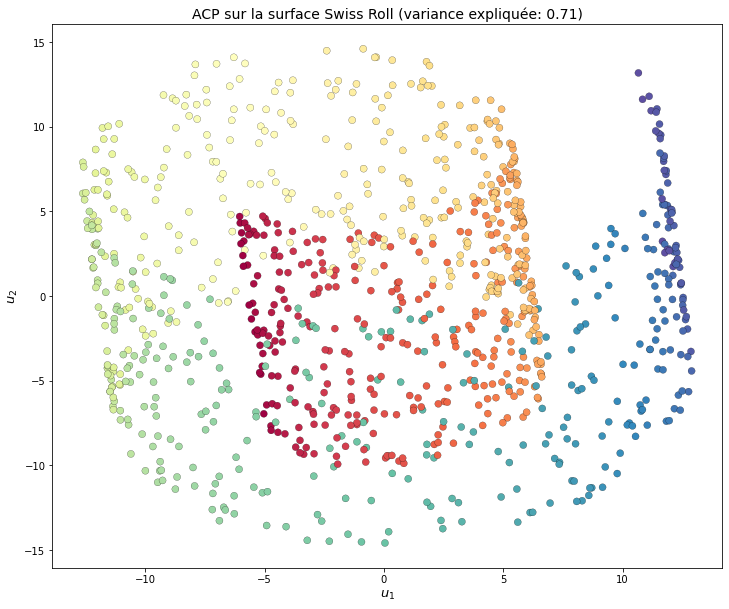
Fig. 126 L’analyse en composantes principales sur le gâteau roulé extrait les directions qui expliquent le plus la variance. La troisième dimension est masquée. Les voisins sont globalement peu préservés. La réduction de dimension « idéale » n’étant pas linéaire, l’ACP ne répond pas au besoin.¶
L’application de l’algorithme LLE permet toutefois d’obtenir une projection qui n’est que localement linéaire. Cet algorithme de réduction de dimension a donc une plus grande expressivité et permet de dérouler de façon satisfaisante le Swiss Roll. Par rapport à l’ACP, il est important de noter que LLE conserve les relations de voisinage: des observations voisines dans l’espace de départ demeurent voisines lorsqu’elles sont projetées dans l’espace réduit. Cette propriété est généralement celle que l’on cherche à conserver quand on s’intéresse à la réduction de dimension non-linéaire.
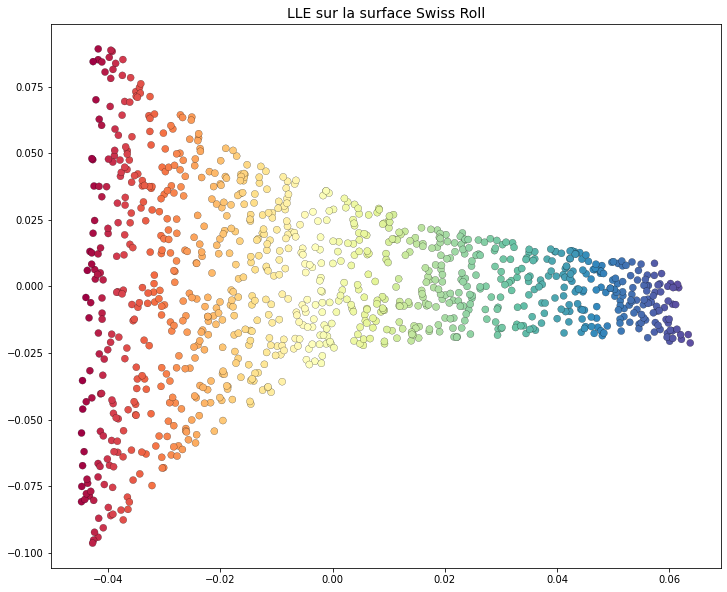
Fig. 127 L’application de Locally Linear Embedding permet de « dérouler » la surface du jeu de données. L’approche par voisinage permet de passer en proche en proche en respectant la structure locale (linéaire).¶
Le plongement dans l’espace à deux dimensions de la figure Fig. 127 illustre une notion particulièrement importante de la réduction non-linéaire de dimension. Notre objectif est de préserver la structure locale du jeu de données et, tout particulièrement, les relations de voisinage. LLE ne préserve donc pas les distances. C’est la raison pour laquelle nous observons cet effet « d’entonnoir ». Les points rouges sont plus éloignés les uns des autres que les points violets. Néanmoins, les voisinages sont invariants à l’échelle. Il n’y a donc aucune conclusion à en tirer. D’ailleurs, dans le roulé suisse de départ, les points rouges ne sont pas plus éloignés que les points bleus. Ce type de distorsion est fréquent dans les visualisations obtenues par LLE et ne doit pas être interprété comme représentatif de la structure des données. Seules les relations de voisinages (et donc la structure locale) est préservée par cet algorithme.
t-SNE: t-distributed Stochastic Neighbor Embedding¶
t-SNE [MH08] est un algorithme de réduction de dimension non-linéaire particulièrement répandu. Son principe général est similaire à celui de LLE: chercher un jeu de données dans un espace de dimension réduite qui présente les mêmes structures locales au voisinage de chaque point. Cependant, t-SNE généralise la notion de voisinage déterministe de LLE à une notion probabiliste. On cherchera non plus à conserver les voisins d’une observation, mais plutôt à conserver les probabilités que d’autres observations lui soient voisines.
Voisinages et probabilités¶
Considérons une matrice d’observations \(\mathbf{X}\) de \(n\) observations de dimensions \(D\). Le voisinage d’un point \(x_i \in \mathbf{X}\) est représenté par la probabilité conditionnelle \(p_{i,j} = p(x_j|x_i)\) pour toute observation \(x_j \in \mathbf{X}\). Cette probabilité représente la probabilité que \(x_j\) soit considéré comme étant un voisin de \(x_i\). Pour que cette définition tienne, cette valeur de probabilité devra bien entendu être entre 0 et 1 et décroître avec la distance entre \(x_i\) et \(x_j\). L’objectif de t-SNE est de déterminer le nuage de points représenté par les observations réduites \(y_i\) de telle sorte à ce que \(p(y_j|x_i) \simeq p(x_j|x_i)\) pour tous les couples \((i,j)\).
Pour concrétiser cette probabilité, t-SNE la définit de la façon suivante :
avec pour convention \(p_{i,i} = 0\) (\(x_i\) n’est pas voisin de lui-même). Le dénominateur de l’équation (48) permet de normaliser les probabilités conditionnelles de sorte à ce que \(\sum_j p_{i,j} = 1\). Le numérateur représente la similarité entre \(x_i\) et \(x_j\), représentée par la valeur de la densité d’une gaussienne centrée en \(x_i\). Intuitivement, cela revient donc à placer un noyau gaussien d’écart-type \(\sigma\) centré sur l’observation \(x_i\). La densité de probabilité qu’un point \(x_j\) soit voisin de \(x_i\) s’obtient donc de façon analogue à l’estimation de densité par la méthode des noyaux en utilisant un noyau gaussien.
Remarquons que cette définition introduit un paramètre de t-SNE: l’écart-type \(\sigma\) qui se trouve au dénominateur dans l’exponentielle. On appelle ce paramètre la perplexité. La perplexité contrôle l’étroitesse du noyau gaussien et va donc permettre de contrôler la « taille » du voisinage de chaque point. Plus cette perplexité est faible, plus la probabilité décroît rapidement avec la distance entre \(x_i\) et \(x_j\).
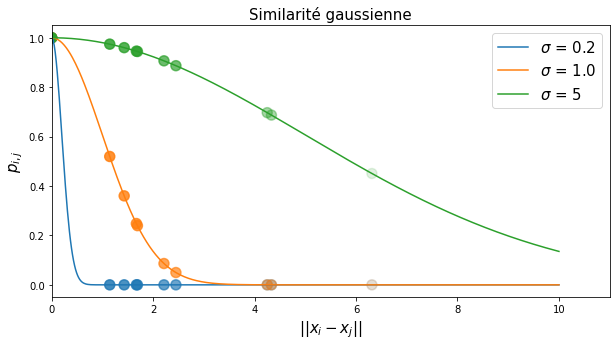
Fig. 128 Valeur de la similarité gausienne en fonction de la distance euclidienne entre \(x_i\) et \(x_j\).¶
Comme pour LLE, nous cherchons donc désormais une matrice réduite \(\mathbf{Y}\), de dimension \(d < D\) de sorte à ce que les probabilités conditionnelles \(q_{i,j} = p(y_j|y_i)\) soient les plus proches possible de \(p_{i,j}\). Un inconvénient de la similarité gaussienne est sa décroissance rapide. Cela permet de facilement distinguer les voisins (proches de \(x_i\)) des non-voisins, pour qui la similarité sera quasi-nulle compte-tenu de la queue « courte » de la gaussienne. Cette propriété est utile dans l’espace de départ mais moins dans l’espace d’arrivée. En effet, supposons que l’on souhaite projeter les données dans un plan, donc un espace à deux dimensions, pour la visualisation. Si l’on utilise une similarité gaussienne, alors les voisins seront agglutinés pour être dans la zone non-nulle de la gaussienne. En effet, pour un même nombre de points, il y a moins de « volume » disponible en 2D que dans un espace à \(n\) dimensions. Les points qui sont voisins se retrouveront placés très proches les uns des autres, tandis que les non-voisins pourront être placés n’importe où ailleurs, puisque la similarité vaut de toute façon zéro. Autrement dit, en utilisant une similarité gaussienne dans l’espace d’arrivée, on risque de produire une visualisation avec de nombreux points qui se chevauchent, séparés par de grands espaces de vide. On appelle ce problème le problème de « l’agglutinement » (ou crowding problem).
Pour éviter ce problème d’agglutinement, t-SNE utilise une autre définition de la probabilité conditionnelle dans l’espace réduit, qui va encourager les points à se disperser dans le plan. La similarité pour les observations réduites \(y_i\) utilise la fonction représentant une distribution \(t\)-Student à 1 degré de liberté :
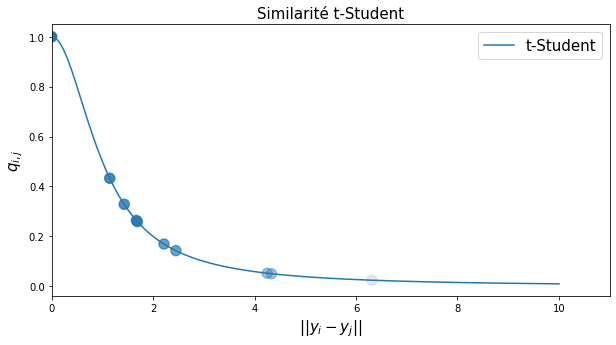
Fig. 129 Valeur de la similarité t-Student en fonction de la distance euclidienne entre \(y_i\) et \(y_j\).¶
Cette fonction exhibe une décroissance rapide (mais moins rapide que l’exponentielle) permettant de distinguer les voisins des non-voisins, mais surtout une queue longue, qui va permettre de mieux répartir les points dans l’espace d’arrivée, cf. Fig. 130.
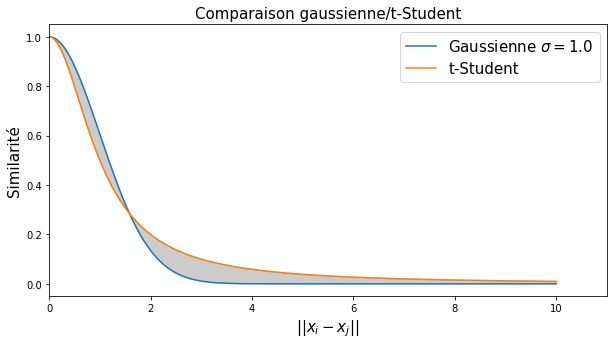
Fig. 130 Comparaison de la similarité gaussienne et la similarité Student.¶
Reste maintenant à déterminer les positions des observations réduites \(y_i\) de sorte à ce que \(q_{i,j} \simeq p_{i,j}\).
Divergence de Kullback-Leibler¶
Puisque \(p\) et \(q\) sont des probabilités, nous avons besoin d’une mesure qui nous indique si deux densités de probabilités sont proches ou très différentes. Cette mesure n’a pas besoin d’être une distance au sens mathématique mais doit tout de même nous garantir que si elle est nulle, alors les distributions \(p\) et \(q\) sont identiques. L’option retenue par t-SNE est d’utiliser la divergence de Kullback-Leibler, qui se définit de la façon suivante dans le cas où de probabilités discrètes :
Cette quantité représente à quel point les distributions \(p\) et \(q\) sont différentes. En particulier, on peut montrer que lorsque \(KL(p|q) = 0\), alors \(p\) et q sont identiques. En effet:
où \(i\) parcourt toutes les valeurs possibles de la variable aléatoire \(P\). Le logarithme étant une fonction concave, l”inégalité de Jensen donne :
et l’égalité est vraie si, et seulement si, la fonction \(\frac{Q(i)}{P(i)}\) est constante. Notons \(\lambda\) la valeur de cette constante. Alors l’égalité est vérifiée si, et seulement si, \(Q(i) = \lambda \cdot P(i)\) quel que soit \(i\). Or, \(P\) et \(Q\) étant des probabilités, la somme des probabilités vaut 1, c’est-à-dire \(\sum_i P(i) = 1\). La seule valeur possible pour cette constante est donc \(\lambda = 1\).
En résumé, nous avons donc une égalité \(KL(p|q) = 0\) si et seulement P(i) = Q(i) pour tout \(i\). En d’autres termes, si la divergence de Kullback-Leibler entre deux probabilités est nulle, alors les distributions sont égales et inversement. Nous pouvons donc essayer de minimiser cette divergence pour rapprocher la distribution \(Q\) de la distribution de référence \(P\).
Algorithme de t-SNE¶
Dans t-SNE, nous voulons rapprocher les distributions \(p_{i,j}\) et \(q_{i,j}\). Comme nous venons de le voir, il suffit de minimiser leur divergence de Kullback-Leibler pour atteindre cet objectif. Pour ce faire, nous pouvons utiliser un algorithme de descente de gradient sur les points \(y_i\) :
Pour chaque paire de points \((x_i, x_j)\), calculer les probabilités conditionnelles
\[p_{i,j} = \frac{\exp(-\lVert x_i - x_j\rVert^2 / 2\sigma^2)}{\sum_{k\neq i} \exp(-\lVert x_k - x_i \rVert^2 / 2\sigma^2)}\]Initialisation: Placer aléatoirement les \(n\) points réduits \(y_1, y_2, \dots, y_n\) dans l’espace de dimension \(d\)
Tant quel’optimisation n’a pas convergé ou que le nombre maximal d’itérations n’est pas atteint:
Calculer les probabilités conditionnelles \(y_{i,j}\) par l”(49).
Calculer le gradient de la divergence de Kullback-Leibler par rapport à \(y_i\) :
\[\frac{\delta L}{\delta y_i} = 4 \sum_j (p_{i,j} - q_{i,j})(y_i - y_j)(1 + \lVert y_i - y_j \rVert^2)^{-1}\]Déplacer chaque point \(y_i\) en suivant la plus forte pente (une itération de la descente de gradient) avec un pas \(\alpha\)
\[y_i := y_i - \alpha \frac{\delta L}{\delta y_i}\]
Fin tant que
Note
Le calcul permettant d’obtenir l’expression analytique du gradient de la fonction de coût \(\frac{\delta L}{\delta y_i}\) est détaillé dans l’annexe A de [MH08].
Autres fonctions de similarité
Remarquons que l’étape 1 de l’algorithme peut être ignorée s’il existe déjà une matrice de similarités \(\mathbf{S} = (p_{i,j})\) pré-calculée sur le jeu de données. En pratique, il n’est donc pas indispensable d’utiliser la similarité gaussienne définie par (48). N’importe quelle métrique de similarité peut-être utilisée pour construire la matrice des probabilités conditionnelles. Le module TSNE de scikit-learn accepte notamment de nombreuse métriques, non nécessairement euclidiennes, et il est même possible de passer une matrice de similarité arbitraire précalculée. Cela peut notamment être utile pour appliquer t-SNE sur des données mixtes, en utilisant une fonction ad hoc capable de définir une similarité pour des variables catégorielles notamment.
Initialisation de t-SNE¶
Comme toutes les méthodes par descente de gradient, l’algorithme d’optimisation de t-SNE est sensible à son initialisation. Le placement initial des points \(y_i\) étant aléatoire, les résultats obtenus par application de t-SNE peuvent fortement varier d’une exécution à une autre. Par ailleurs, t-SNE ne préserve que les voisinages. C’est donc un algorithme qui se concentre sur la structure locale, au détriment de la préservation de la structure globale.
Pour pallier ces deux limitations, une alternative consiste à d’abord appliquer une analyse en composantes principales et de ne conserver que les \(d\) premières composantes. Le nuage de points projeté peut ainsi servir d’initialisation aux observations réduites \(y_i^0\) avant la phase d’optimisation par descente de gradient. Du point de vue théorique, cette initialisation a deux avantages :
Une meilleure préservation de la structure globale grâce à l’ACP;
Une plus grande reproductibilité en supprimant la stochasticité liée à l’initialisation.
En pratique, cette initialisation est plus robuste et elle généralement appliquée par défaut dans les bibliothèques qui implémentent t-SNE.
Choix de la valeur de perplexité¶
La perplexité est le principal paramètre à régler lors de l’application de t-SNE. Intuitivement, \(\sigma\) contrôle la taille du voisinage considéré et peut ainsi être relié au nombre de voisins \(k\) dans LLE.
Une perplexité faible restreint fortement les observations qui sont définies comme voisines l’une de l’autre. Seules des observations très proches auront une similarité non-nulle. Cela accentue la préservation de la structure locale. À l’inverse, une perplexité élevée inclue presque toutes les observations dans le voisinage de toutes les autres, à l’exception des plus éloignées. Cela permet ainsi de mieux capturer la structure globale du nuage de points, au détriment des détails locaux, comme illustré dans la Fig. 131.
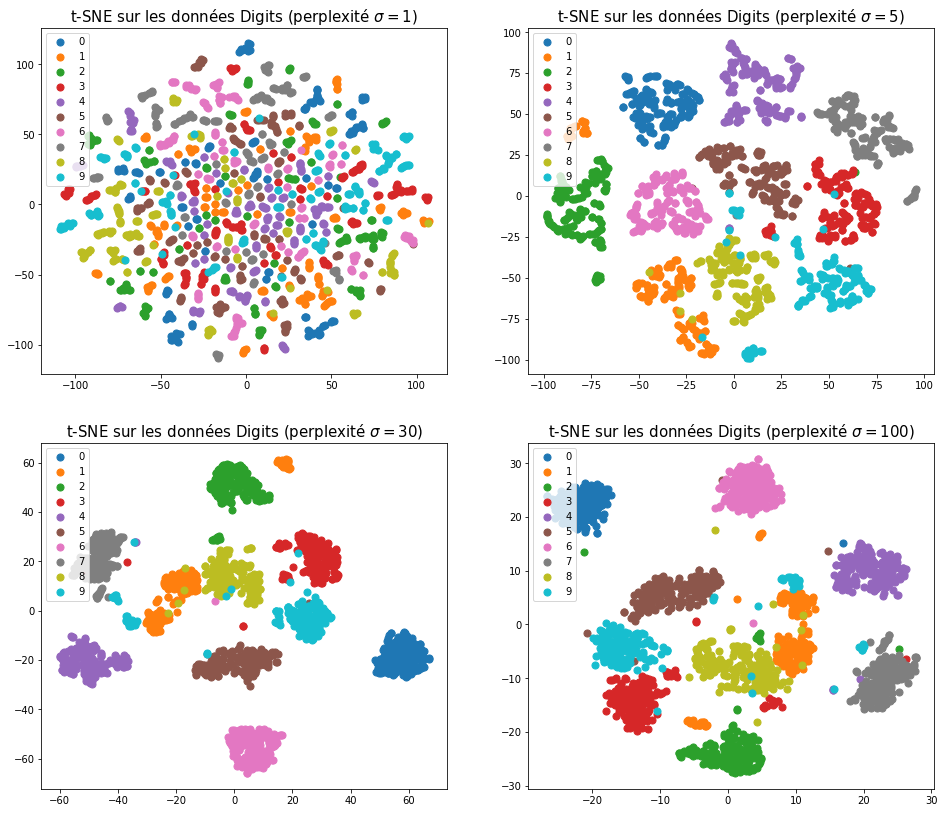
Fig. 131 Application de t-SNE sur le jeu de données Digits pour différentes valeurs de perplexité \(\sigma\).¶
En pratique, il est recommandé d’expérimenter plusieurs valeurs de perplexité et de croiser les interprétations au niveau local et au niveau global.
Optimisation¶
L’algorithme décrit plus haut pour t-SNE passe sous silence une astuce d’implémentation qui permet d’accélérer la convergence de la descente de gradient. En pratique, t-SNE est implémenté en deux phases:
une phase dite d’exagération précoce (early exaggeration), durant laquelle toutes les probabilités conditionnelles \(p_{i,j}\) dans l’espace initial sont multipliées par un facteur \(\gamma\). Cela permet d’augmenter artificiellement la séparation des groupes naturellement présents dans les données et de placer plus rapidement les observations réduites \(y_i\) près de leur position optimale.
une phase d’optimisation finale durant laquelle les valeurs réelles des probabilités conditionnelles sont utilisées, pour affiner le placement des observations réduites localement au sein de chaque groupe.
Des heuristiques plus ou moins sophistiquées existent afin de déterminer les valeurs des paramètres d’exagération et du pas d’apprentissage, comme celles décrites dans [BCA19]. Il n’est généralement pas utile de modifier ces paramètres.
En pratique, l’exagération précoce est appliquée pendant 250 itérations de la descente de gradient, puis l’optimisation se poursuit avec les valeurs normales des probabilités conditionnelles jusqu’à atteindre le critère d’arrêt (convergence ou nombre d’itérations maximale).
UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction¶
UMAP (Uniform Manifold Approximation & Projection) [MHM18] est un algorithme de réduction non-linéaire de dimension dont le principe est semblable à celui de t-SNE. Comme précédemment, nous allons chercher une représentation des données en plus faible dimension qui présente la même topologie que le nuage des observations dans l’espace de départ. Pour ce faire, nous allons construire une matrice de similarités représentant la similarité entre chaque paire de points, puis nous chercherons l’ensemble des points dans l’espace d’arrivée qui vérifie le même graphe de similarité. La principale différence entre t-SNE et UMAP vient de leur définition de cette notion de similarité. UMAP définit une affinité de façon locale autour de chaque point, avec une perplexité dépendant de la densité du voisinage.
Similarité dans l’espace de départ¶
La similarité \(p_{i|j}\) entre deux observations \(x_i,\) et \(x_j\) est définie comme étant :
\(\rho_i\) est défini comme la distance entre \(x_i\) et son plus proche voisin, c’est-à-dire : \(\rho_i = \min_{j \neq i} \lVert x_i - x_j \rVert\)
\(\sigma_i\) est fixé de sorte à ce que \(0 \leq p_{i|j} \leq 1\), c’est-à-dire :
\(k\) est un paramètre réglant le nombre de plus proches voisins à considérer, c’est-à-dire la taille du voisinage envisagé.
Cette similarité définit un noyau gaussien adaptatif qui est proche de celui utilisé pour t-SNE, avec deux différences : - la similarité ne commence qu’à décroître qu’au-delà du plus proche voisin (lorsque la distance \(d(x_i, x_j) > \rho_i\)), - la perplexité dépend de la densité du voisinage.
Pour deux points \(x_i\) et \(x_j\), la probabilité jointe \(p_{i,j}\) d’appartenir à un même voisinage doit être symétrique (\(p_{i,j} = p_{j,i}\)). Une façon de symétriser l’équation précédente est de définir :
La symétrisation est nécessaire car \(\rho_i \neq \rho_j\). Pour rappel, t-SNE utilise une autre symétrisation : \(p_{i,j} = \frac{p_{i|j} + p_{j|i}}{2N}\).
Similarité dans l’espace d’arrivée¶
Comme pour t-SNE, on souhaite éviter l’agglutinement des points dans l’espace d’arrivée : de faibles variations de similarité dans l’espace de départ doivent correspondre à des variations significatives de distance dans l’espace d’arrivée. Cela correspond à chercher une distribution des similarités dans l’espace d’arrivée avec une queue épaisse.
La solution adoptée par UMAP consiste à utiliser une loi de similarité inspirée de la loi \(t\) de Student :
\(a\) et \(b\) étant des paramètres réglables. En pratique, la fonction idéale n’autoriserait jamais deux points dans l’espace d’arrivée à être plus proche qu’une certaine distance minimale min_dist. Sur le segment \([0, \text{min\_dist}]\), la similarité serait considérée comme égale à 1. Puis on tolérerait une décroissance exponentielle douce de la similarité. Cela correspond à une fonction définie par morceaux :
En pratique, c’est le paramètre min_dist que l’on pourra régler dans UMAP. Dans l’équation de la similarité, le choix des paramètres \(a\) et \(b\) est ainsi fait automatiquement de sorte à ce que la similarité qui en résulte soit la plus proche possible de la fonction idéale définie par morceaux.
Optimisation¶
L’objectif est de trouver la distribution des points \(y_i\) dans l’espace d’arrivée telles que les similarités \(q_{i,j}\) s’approchent le plus possibles des similarités \(p_{i,j}\). Autrement dit, on souhaite faire tendre la distribution \(q\) vers la distribution \(p\).
En pratique cela revient à minimser une fonction objectif d’entropie croisée, qui mesure la dissimilarité entre les deux distributions \(p\) et \(q\) :
qui s’écrit également \(CE(p,q) = H(p) + D_\text{KL}(p || q)\) où
\(H(p) = \sum_{i=1,j=1}^n p_{i,j} \log \left(\frac{1}{p_{i,j}} \right)\) est l’entropie de Shannon de \(p\),
\(D_\text{KL}\) est la divergence de Kullback-Leibler.
Comme \(H(p) \geq 0\), \(\operatorname{CE}(X,Y) \geq D_\text{KL}(p||q)\) et minimiser l’entropie croisée revient à minimiser la divergence de Kullback-Leibler et donc à faire tendre \(q_{ij} \rightarrow p_{ij}\).
Contrairement à t-SNE qui minimise la fonction objectif par descente de gradient directe en calculant la divergence KL sur l’ensemble des données, UMAP accélère le calcul de en réalisant une descente de gradient stochastique et estime l’entropie croisée sur un échantillon de quelques dizaines ou quelques centaines de points. L’échantillon est construit de sorte à contenir un mélange de voisins (\(p_{ij} \simeq 1\)) et de non-voisins (\(p_{ij} \simeq 0\)) de sorte à optimiser les deux termes de l’entropie croisée simultanément.
La mise à jour des points dans l’espace d’arrivée se fait de manière analogue à t-SNE :
où \(\alpha\) est le pas d’apprentissage de l’algorithme de descente de gradient. Le gradient \(\frac{\delta \text{CE}}{\delta y_i}\) dispose d’une expression analytique, comme pour t-SNE.
Réduction de dimension semi-supervisée¶
Une contribution intéressante en pratique de UMAP est l’extension de la notion de similarité pour prendre en compte des éventuelles connaissances a priori sur les données. Considérons un jeu de données contenant des {étiquettes de groupes: \(\mathcal{X} = \{(x_1, l_1), \dots, (x_n, l_n)\}\) avec \(x_i\) les observations et \(l_i\) les étiquettes (variables catégorielles).
Pour inclure la connaissance des étiquettes dans l’algorithme, UMAP définit une distance mixte sur le couple \((x_i, l_i)\) :
La distance totale impliquée dans le calcul des similarités entre points dans l’espace de départ s’obtient par une somme pondérée par un paramètre \(\lambda\) :
où \(d^\text{obs}\) représente la distance habituelle dans l’espace de départ, qui s’applique sur les données \(x_i\). Typiquement, dans la définition précédente, \(d^\text{obs}(x_i, x_j) = \lVert x_i - x_j \rVert\) la distance euclidienne.
Cette nouvelle distance remplace ainsi la distance euclidienne dans (50).
Le paramètre \(\lambda\) permet de contrôler l’importance donnée à la sémantique ou aux données:
\(\lambda = 0 \rightarrow\) seule la distance entre les données \(x_i\) est prise en compte
\(0 < \lambda < 1 \rightarrow\) la distance totale est une moyenne de la distance entre les observations et entre les étiquettes. Par défaut, \(\lambda = 0.5\) et il s’agit d’une moyenne équilibrée.
\(\lambda = 1 \rightarrow\) seule la distance entre les étiquettes est prise en compte
A.C. Belkina, C. O. Ciccolella, R. Anno, R. Halpert, J. Spidlen, et J. E. Snyder-Cappione. Automated optimized parameters for T-distributed stochastic neighbor embedding improve visualization and analysis of large datasets. Nature Communications. 10(1):5415, Nov. 2019.
Laurens van der Maaten et Geoffrey Hinton. Visualizing Data using t-SNE. Journal of Machine Learning Research. 9(86):2579-2605, Nov. 2008.
Lawrence McInnes, John Healy et James Melville. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv:1802.03426, 2018.
Sam T. Roweis et Lawrence K. Saul. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science, 290:2323-2326, Dec. 2000.
Lawrence K. Saul et Sam T. Roweis. An Introduction to Locally Linear Embedding, 2000.
