Travaux pratiques - Introduction à Processing

Références externes utiles :

• Téléchargement et documentation Processing

Exercice 1 - Processing en mode immédiat

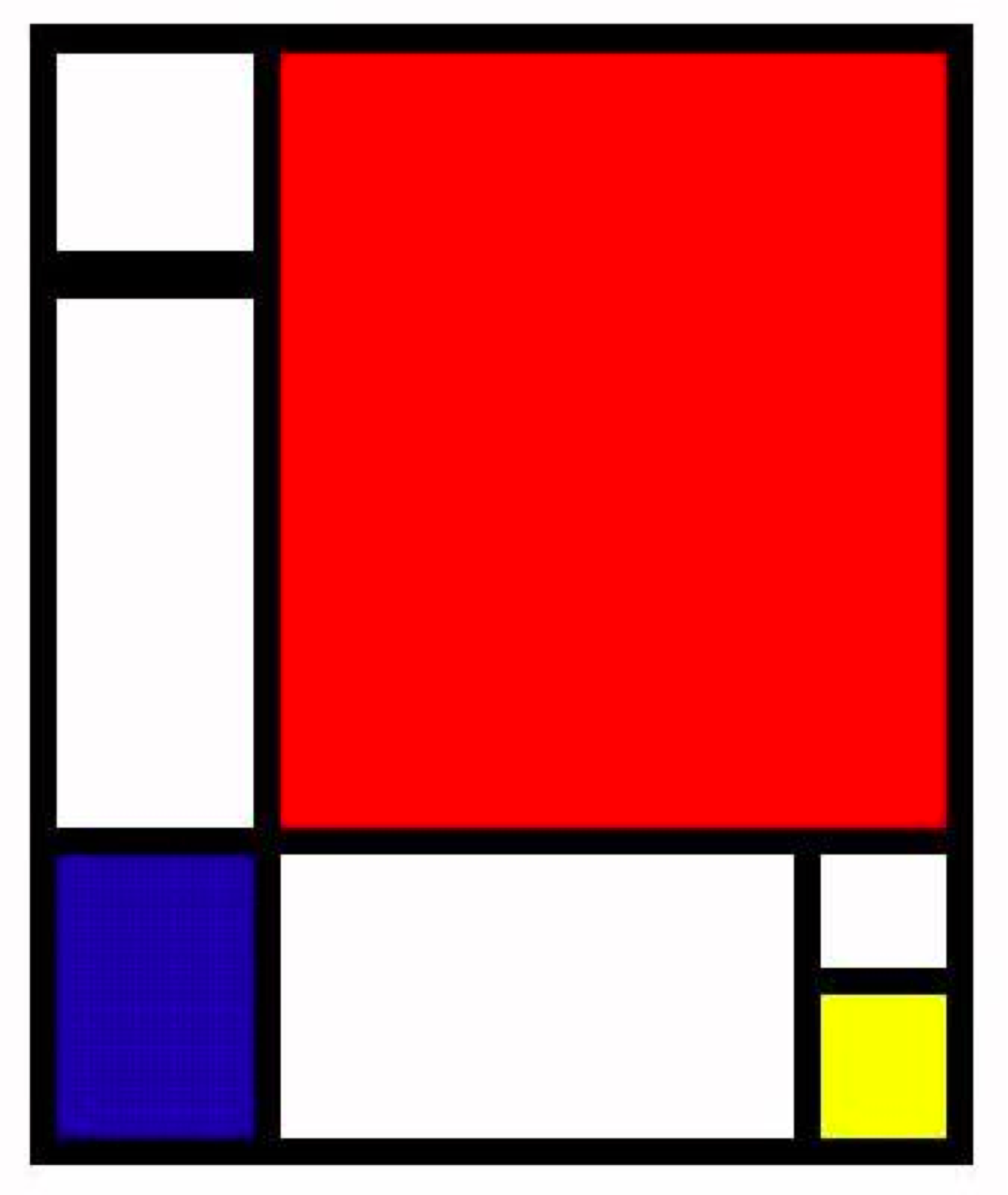
Ecrire le code Processing correspondant à chacune des trois images ci-dessous. La première utilise seulement des primitives de tracé et s’inspire d’un tableau de Mondrian. La deuxième nécessite des boucles et du (pseudo)hasard, elle s’inspire de Le Parc et Vasarely. La troisième demande de la récursivité.

Exercice 2 - La boucle d’animation draw()

Un grand classique de l’animation procédurale est le mouvement brownien. Créer une classe Particule avec des attributs de position (x,y), une méthode de dessin et une autre pour la mise à jour de position. Pour cette dernière, on se contente d’incrémenter les coordonnées selon une valeur (pseudo)aléatoire de quelques pixels (en plus ou en moins). Créer ensuite un tableau d’un bon nombre N d’objets particule. Etudier le comportement du programme (en terme de framerate) avec N croissant et selon le type des primitives de tracé utilisées pour les particules (ellipses ou rectangles, par exemple).

Exercice 3 - Mode réactif pour l’interaction

Ajouter au programme précédent deux boutons (start et stop), qu’il faut coder soi-même. Créer une classe Button qui s’en charge. Etudier ensuite une classe Slider, qui par exemple ici pourrait faire évoluer le diamètre des particules en temps réel.

Reprendre ensuite l’exercice avec à la place les composants de GUI de la librairie controlP5 (qu’il faut installer soi-même).